金融数学的现状与发展

薛佳佳，乔路芳

(中国矿业大学 理学院，江苏 徐州 221116)

0 引言

金融数学是最近发展起来的新兴边缘学科，是数学与金融学的交叉。主要运用现代数学理论和方法(如：随机分析、随机最优控制、组合分析、非线性分析、多元统计分析、数学规划、现代计算方法等)对金融(除银行功能之外，还包括投资、债券、基金、股票、期货、期权等金融工具和市场)的理论和实践进行数量的分析研究，其目的是利用有效的数学工具揭示金融学的本质特征，从而达到对具有潜在风险的各种未定权益的合理定价和选择规避风险的最优策略[1-3]。

金融数学(Mathematical Finance)这一学科名词20世纪80年代末才出现。它是马柯维茨(H.Markowitz,1990年获诺贝尔经济学奖)的证券组合选择理论和斯科尔斯默顿(M.Scholes-R.Merton，1997年获诺贝尔经济学奖)的期权定价理论这两次华尔街革命的直接产物[4]。但金融数学的历史可以追朔到1900年法国数学家巴歇里埃(Bachelier L.)的博士论文“投机的理论”(The Theory of Speculation)，该文中巴歇里埃首次使用Brown 运动来描述股票价格的变化，这为后来金融学的发展，特别是为现代期权定价理论奠定了理论基础。金融数学的核心问题是不确定环境下的最优投资策略的选择理论、定价理论以及市场理论，套利、最优与均衡是其中的三个主要概念[4-5]。

1 金融数学中的数学理论和方法

金融数学作为一门边缘学科，它最显著的特征就是有效地运用数学方法发现和论证金融经济运行的一些规律。由于金融问题的复杂性，所用到的数学知识，除基础知识外，还大量地运用现代数学理论和方法。主要有倒向随机微分方程、随机分析、随机控制、数学规划、微分对策、非线性分析、数理统计、泛函分析、鞅理论等，在证券价格分析中还引进了新型的非线性分析工具，如分形几何、混沌学、子波理论、模式识别等。在证券选择和股票种类的预测中逐渐引入神经网络方法、人工智能方法，在期货市场创新的仿真研究中有人运用模拟退火法和遗传算法等[6]。

2 金融数学的基础理论

2.1 证劵组合理论

金融学从定性分析到定量分析的转变始于马柯维茨(Markowitz)的证劵组合投资。1952 年，马柯维茨在其论文 “投资组合的选择(Portfolio Selection)”中将概率论和数学规划成功地组合在一起，把组合投资中的股票价格作为随机变量，以均值衡量收益，用方差表示风险。当收益一定，使风险最小的组合投资问题可以归三结为求如下的二次规划的最优解：

(1)

其中：X=(X1,X2,…,Xn)T为所求的组合系数；R=(R1,R2,…Rn)T为收益的均值向量；V为收益协方差矩阵；r为投资者要求的最低收益率；I=(1,1,…,1)T，L=(L1,L2,…Ln)T，P=(P1,P2,…Pn)T为买空卖空的限制。

马柯维茨首次提出用方差来度量投资组合的风险，还提出了投资组合的有效边界的概念：即均值一定时方差最小的点，方差一定时均值最大的点组成的集合。他认为，个人投资组合的最优决策是选择个人的无差异曲线与投资组合的有效边界的切点，并进而求出各资产持有的合理的比例。

2.2 CAPM理论

20世纪60年代中期，在马柯维茨的均值-方差投资组合理论的基础上，斯坦福大学教授夏普(William Sharpe)、林特纳Lintner J.)和莫新(Mossin J.)研究了均衡竞争市场中金融资产的价格形成，提出了著名的资本资产定价理论(Capital Asset Pricing Model，简称CAPM)[7-9]。

E(R1)=RF÷βi(E(Rm)-RF)

(2)

其中，RF为无风险资产的收益率；Rm为市场资产组合的收益率；β=cov(Ri,Rm)/var(Rm)为风险系数。

他们认为，证券投资的回报率与风险之间存在一定的定量关系，所有投资者都在证券市场线上选择证券，所选中的投资组合是投资者的效用函数与证券市场线的切点，夏普评价的关键就是求切点，即测度资本市场线中的斜率项。CAPM 在证券股价、投资组合的绩效的测定、资本预算和投资风险分析中得到广泛应用。

2.3 Black-Scholes 期权定价理论

1973年，布莱克(Fisher Black)和斯科尔斯(Myron S.Scholes)在“期权定价与公司负债”一文中提出了著名的Black-Scholes模型(简称B-S 模型)[10]：

(3)

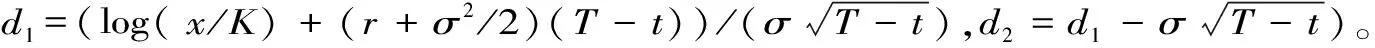
由此证明了期权的合理价格不依赖于投资者的偏好，也就是“风险中性原则”，这点不同于之前的无套利定价原理。由于B-S 公式具有较强的实用性和可操作性，B-S模型可以被广泛用来制作各种金融衍生产品的价格，是开发新金融产品的有效工具。B-S模型也为套期保值与风险管理开辟了新的天地，成为现代金融理论探索的源泉。几乎与此同时，默顿(Merton R)在“合理的期权定价理论”一文中对B-S模型和定价公式做了多方面的系统推广，他研究出了表示股票支付红利的期权定价公式；给出了欧式看涨期权和看跌期权以及欧式看跌期权的定价公式；提出了更贴近现实的可变利率的欧式期权定价模型。

3 金融数学研究的最新进展

20世纪80年代末，随着金融市场的进一步完善和发展，人们发现前面研究的所有金融模型都假定投资者可得到市场的完全信息，而实际上投资者只可观测到刻画系统状态的价格过程本身，而布朗运动及动态资产的漂移系数是不可观测到的，即投资者只可得到市场的部分信息[3]。于是，许多学者运用各种数学方法对基于不完全信息的投资消费问题进行了系统研究，并取得了一定的进展。本文现将研究中所用到的主要数学工具列举如下：

3.1 随机最优控制理论

由于金融学理论一个得重要的应用领域是解决连续时间的随机性的问题，而解决这个问题的重要手段是随机最优控制理论。随机最优控制是在20世纪60年代末和70年代初，数学家们应用贝尔曼最优化原理，并用测度理论和泛函分析方法发展起来的新的数学研究领域。1971年默顿(Merton)使用连续时间方法论述消费和资产组合的问题[11]，有布罗克(Brock)和米尔曼(Mirman)在不确定情况下使用离散时间方法解决经济最优增长问题[12]。从此以后，随机最优控制方法应用到大多数的金融领域。在国内以彭实戈为代表的中青年学者对此也做出了卓越贡献[13-16]。

3.2 鞍理论

鞍理论引入是现代金融理论最新的研究成果。1977年，哈里森(Harrison J.M.)和柯瑞普斯(Kreps S.R.)提出了期权定价理论的鞅方法，他们用鞅论中的鞅测度概念来刻画无套利市场和不完全市场，并用等价鞅测度对期权进行定价和套期保值或对冲。由Karatza.S和Shreve等人倡导的鞍方法直接把鞍理论引入到现代金融理论中，利用等价鞍测度的概念研究衍生证券的定价问题，得到的结果不仅能深刻揭示金融市场的运行规律，而且可以提供一套有效的算法，求解复杂的衍生金融产品的定价与风险管理问题[17-18]。利用鞍理论研究金融理论的另一个作用是它能够较好地解决金融市场不完备时的衍生证券定价问题，从而使现代金融理论取得了突破性的进展[19]。目前基于鞍方法的衍生证券定价理论在现代金融理论中占主导地位，但在国内还是一个空白。

3.3 微分对策理论

运用微分对策方法研究期权定价问题和投资决策问题是现代金融理论发展的另一个重要方向，目前取得了一定的成果[20-21]。当金融市场不满足稳态假定或出现异常波动时，证券价格往往不服从几何布朗运动，这时用随机动态模型研究证券投资决策问题的方法无论从理论上，还是从实际上都存在着较大偏差。用微分对策方法研究金融决策问题可以放松这一假设，把不确定扰动假想成敌对的一方，针对最差情况加以优化，可以得到“鲁棒性”很强的投资策略。另外，求解微分对策的贝尔曼方程是一阶偏微分方程，比求解随机控制问题的二阶偏微分方程要简单得多。因此，运用微分对策方法研究金融问题具有广阔的应用前景。

3.4 最优停时理论

最优停时理论是概率论体系中一个具有很强的实用性领域，近年来，不少金融学家和金融数学家将这一理论与现代的投资组合理论相结合，取得了不错的成绩[22-24]。但是这一领域的研究文献仍然不多，该领域仍处于起步阶段。Moton A和Pliska S R运用最优停时理论研究了具有固定交易费用的证券投资决策问题，给出了具有二个风险证券的投资决策问题一种简化算法。在国内有关这方面的研究尚不多见。相信运用最优停时理论来研究投资决策问题和风险最小化问题会有更大的进展。

3.5 智能优化

把智能优化方法(遗传算法、模拟退火算法、人工神经网络、小波分析等)和传统方法结合起来，应用于风险控制和投资决策问题中是另一个具有更为广阔的研究领域，给我们提供了广泛的研究课题。国际上有关这方面的研究已经有了初步的成果[25-27]，在国内也有一大批学者致力于这方面的研究[28-30]。由于这一领域的发展比较晚，还有很多的难题尚未解决，但是我们仍相信金融学家、数学家以及人工智能专家们的通力合作，在这一新兴的研究领域一定能够取得突破性的进展。

4 金融数学研究面临的问题与前景

金融数学除了上述几个基本理论的继续发展和完善外，还有很多工作可以做。如美式期权问题、亚洲期权问题、利率的期限结构问题、市场价格的波动与突发事件问题等。

4.1 美式期权问题

在市场上交易的期权大部分是美式期权[31]。对于美式期权的定价，问题要比欧式期权定价困难得多。因为美式期权可以在到期前的任何时刻执行，这就涉及到期权的最佳执行时间问题。一般情况下期权的最佳执行时间是一个十分复杂的问题，至今还没有得到很好的解决。如果应用偏微分方程的方法来讨论美式期权的定价，对应的偏微分方程的问题将变成为“自由边界”问题，在数学上较难处理。一般情况下，美式期权没有精确的解析定价公式，而只能用数值解法或解析近似解法，因此，发展各种计算美式期权价格的数值方法具有重要的实际意义。

4.2 利率的期限结构问题

在“B-S模型”中，利率是给定的常数。实际上，利率的变化是相当复杂的，不同性质、不同到期日的证券，利率的变化规律互不相同，这也就是利率的期限结构。它通常可以用收益率曲线的形式来表示。利率的期限结构包括三种理论：市场预期理论、市场分割和投资偏好理论、流动性偏好理论[32-33]。这些理论分别从不同的角度对利率的不规则变化作出了解释。近年来由于利率风险的日益突出，利率期权等利率衍生证券得到了迅速发展，利率的期限结构的数学模型不断提出。

4.3 市场价格波动问题

所谓价格的波动性，通常是指未来价格偏离其期望值的可能性。在金融经济学中，波动性用回报的标准差来度量，而不用价格的标准差度量[31]。例如，在“B-S模型”及其大部分推广中，假设股票价格的波动率为常数，这在实际中是不合理的。为了更准确地描述股票价格变化的规律，必须考虑以下因素：股票价格波动率对股票价格的依赖性；波动率与其它随机变量的依赖性；股票价格可能的突然跳动。随机波动率模型能够体现上述某些因素，目前受到高度重视。这类模型假设波动率服从某一随机过程，比如几何布朗运动等。

4.4 突发事件问题

突发事件在金融领域中具有不容忽视的影响，如1997年的东南亚金融危机，给一些国家造成巨大损失。基于传统的平稳随机过程的预测理论完全不适用。传统理论或许能解释市场在95%的时间里发生的情况。然而，如果人们承认突发事件就发生在剩下5%的时间里，那么传统理论所描述的图景就没有反映实际情况[34]。现在研究应用混沌学与分形理论来解释股票价格如何暴涨暴跌。金融突发事件的预警由于涉及多因素、定量化与报警灵敏度等，往往比较困难，这也是金融数学研究的重要领域。

5 结束语

金融数学是运用数学的理论和方法对金融理论和实践进行的分析研究，它为金融经济的发展注入了巨大的动力，促进了金融理论、金融实践管理和金融创新。随着金融全球一体化的发展，金融数学将成为国际金融领域的一枝奇葩，受到国际金融界和应用数学界的高度重视。我们相信21世纪金融数学将会得到更深入的发展和更广泛的应用。

[参考文献]

[1] 李向科，戚发全.金融数学[M].北京：中国人民大学出版社，2004.

[2] 张友兰，周爱民.金融数学的研究与进展[J].高等数学研究，2004，7(4)：53-55.

[3] 袁军.金融数学研究综述与展望[J].商业时代，2008，(13)：68-69.

[4] Alison Etheridge.金融数学教程[M].北京：人民邮电出版社，2006.

[5] 吴岚，黄海.金融数学引论[M].北京：北京大学出版社，2005.

[6] 孙富.金融数学概述[J].呼伦贝尔学院学报，2005，13(4)：65-66.

[7] Black F.Capital Market Equilibrium with Restricted Borrowing[J].Journal of Business，1972，45(7)：223-248.

[8] Sharpe W.Capital asset prices:a theory of market equilibrium under conditions of risk[J].Journal of Fi-nance，1964，19：425-442.

[9] Mossin J.Eeuilibrium in a capital asset market[J].Econometrica，1966，34(4)：768-783.

[10] Black F.Scholes M.The pricing of options and corporate liabilities [J].Journal of Political Economy，1973，81(3)：637-654.

[11] Merton R.Optimal consumption and portfolio rules in a continuous-time mode[J].Journal of Economic Theory，1971，8(3)：373-413.

[12] Brock W.Mirman L.Optimal economic growth and uncertainty the discounted case[J].Journal of Economic Theory，1972，4：479-513.

[13] Pardoux E.Peng S.Adapted solution of a backward stochastic differential equation[J].Systems and Control Letters，1990，14：55-61.

[14] 彭实戈.倒向随机微分方程及其应用[J].数学进展，1997，26(2)：97-112.

[15] 许世蒙.金融市场建模原则与财富过程的最优增长[J].应用数学学报，1998，21(2)：171-178.

[16] Peng S.A general stochastic maximum principle for optimal control[J].SIAM J Control.1978，14：62-78.

[17] Karatzas I.Shreve S E.Brownian Motion and Stochastic Calculus[M].New York:Spring-er-Verlag，1991.

[18] Karatzas I.Shreve S E.Methods of Mathematical Finance[M].New York:Springer-Verlag，1998.

[19] Krankov D.On the closure of a family of martingale measures and an optimal decomposition of a supermartingale[J].Probabilicty&Application，1996，41(4)：82-89.

[20] 刘海龙，郑立辉，樊治平，等.证劵投资决策的微分对策方法研究[J].系统工程学报，1999，18(1)：69-72.

[21] 郑立辉.基于鲁棒控制的期权定价理论与方法研究[D].武汉：华中理工大学博士后研究工作报告，1999，18(1)：69-72.

[22] 任建方，王石.最优停止定量离散化方法的应用[J].国防科技大学学报，1998，20(2)：114-116.

[23] Morton A.Pliska S.Optimal portfolio management with fixed transaction costs[J].Math Finance，1995，5(4)：337-356.

[24] 金治明.最优停止理论及其应用[M].长沙：国防科技大学出版社，1995：382-396.

[25] Hawley D.Johnson D.Raina D.Artifical Neural Systems:Anew Tool for Financial Decision Making[F].Financial Analysis Journal，1990，46(1)：63-72.

[26] Wong F S.Fuzzy Neural Systems for Stock Selection[J].Financial Analysis Journal，1992，48(1)：47-52.

[27] Krgzanowski L.Using Artificial Neural Network to pick Stocks [J].Financial Analysis Journal，1993，49(4)：21-27.

[28] 黄小原.证劵组合快车道问题的研究[J].信息与控制，1994，23(2)：71-75.

[29] 赵宏，邹雯，汪浩.证劵市场预测的神经网络方法[J].系统工程理论与实践，1997，17(6)：127-131.

[30] 邵良衫，高树林.基于人工神经网络的投资预测[J].系统工程理论与实践，1997，17(2)：67-71.

[31] 瞿绍发，林祥，吴恒煜.金融数学介绍[J].商业研究，2004，28(5)：142-143.

[32] 严加安.金融数学：历史与现状[J].权威论坛，2001，8(1)：64-66.

[33] 王金平，李治.金融数学研究前景展望[J].现代商贸工业，2008(11)：205-206.

[34] 王金平.中外金融数学的发展及其走向[D].济南:山东大学硕士学位论文，2008.