一类五阶牛顿变形方法及其加速

周任沣，蔡 静

（湖州师范学院理学院，浙江 湖州 313000）

一类五阶牛顿变形方法及其加速

周任沣，蔡 静＊

（湖州师范学院理学院，浙江 湖州 313000）

结合经典牛顿法与中点牛顿法，提出了一类求解非线性方程的五阶收敛迭代算法，并建立了该牛顿变形方法的加速公式．数值试验结果表明：相对于经典牛顿法、中点牛顿法、几何平均牛顿法、调和平均牛顿法和Simpson牛顿法等几种已有的牛顿改进格式，此类新型牛顿变形方法的收敛速度更快，精度更高．

非线性方程；收敛阶；数值试验；迭代方法

0 引 言

非线性方程f（x）＝0的求解是当前各学科领域中的重要问题之一．众所周知，绝大多数非线性方程很难进行解析求解，因此，构造非线性方程的近似解法具有非常重要的意义．

牛顿法是一类常用的非线性方程的近似解法，被广泛应用于气象学、统计学、经济学与物理学等领域，也倍受广大科研技术人员的重视．近年来，构造更优的牛顿变形迭代格式倍受关注，许多文献提出了各种改进的牛顿迭代格式，主要有中点牛顿法（MN）、几何平均牛顿法（GN）、Simpson牛顿法（SN）、调和平均牛顿法（HN）等［1－10］．

该文主要考虑如下问题：1）如果在经典牛顿法的基础上结合中点牛顿迭代格式［1］，可以建立什么样的牛顿变形方法，其收敛速度如何？2）该方法结合牛顿下山法的加速思想，能建立怎样的加速公式？针对上述问题，该文将给出一类新的牛顿变形方法及其加速公式并进行收敛性分析．同时通过数值试验，将所建立的牛顿变形方法与已有的几类牛顿改进格式进行比较，以验证该算法的优越性．

1 一类五阶牛顿变形方法

在经典牛顿法的基础上结合中点牛顿迭代格式［1］，可得到：

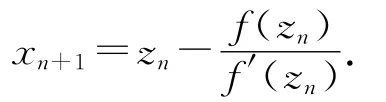
其中n＝0，1，2，…．在此基础上，为了得到f′（zn）显示表达式，在（xn，f′（xn））和（yn，f′（yn））两点上用线性插值，则f′（zn）可近似为

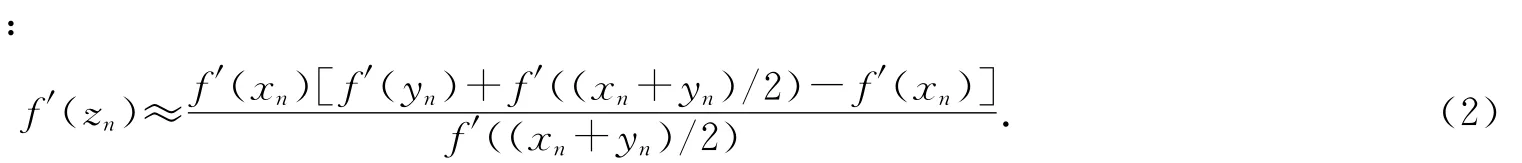
将式（2）代入式（1），得到如下新的迭代算法：

算法1

其中n＝0，1，2，…．将这种新算法记为MC，下面从理论上分析此类新算法的收敛性．先给出收敛阶的定义．

定义1 设序列｛xn｝∞0收敛于α，若存在p≥1及常数C≠0，使成立，则称序列是p阶收敛的．C称为收敛因子，也称为渐近误差常数．

在定义1中，令en＝xn－α，则称关系式en＋1＝Cepn＋o（epn）为此序列的误差方程，p称为收敛的阶．将f（zn）在α处泰勒展开，即得

将式（5）至式（7）代入式（3），可得

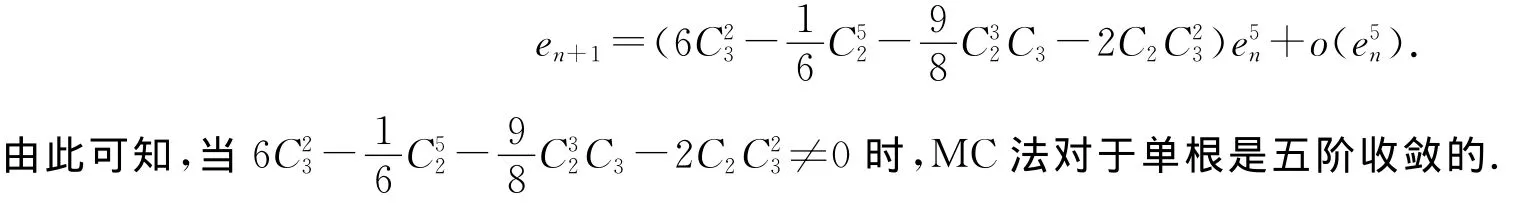
2 五阶牛顿变形方法的加速

将算法1结合牛顿下山法的加速思想，可得如下加速算法：

算法2

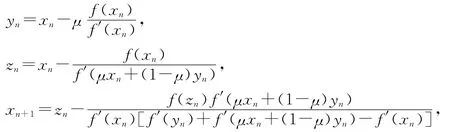
其中0＜μ＜1．

3 数值试验

结果如表1～3所示．表中k为迭代次数，xk为迭代值，fk为每次迭代后的函数值，piancha为相邻两次迭代的偏差，xdpiancha为相邻两次迭代偏差的相对误差，这里取迭代次数的最大值gxmax＝100．

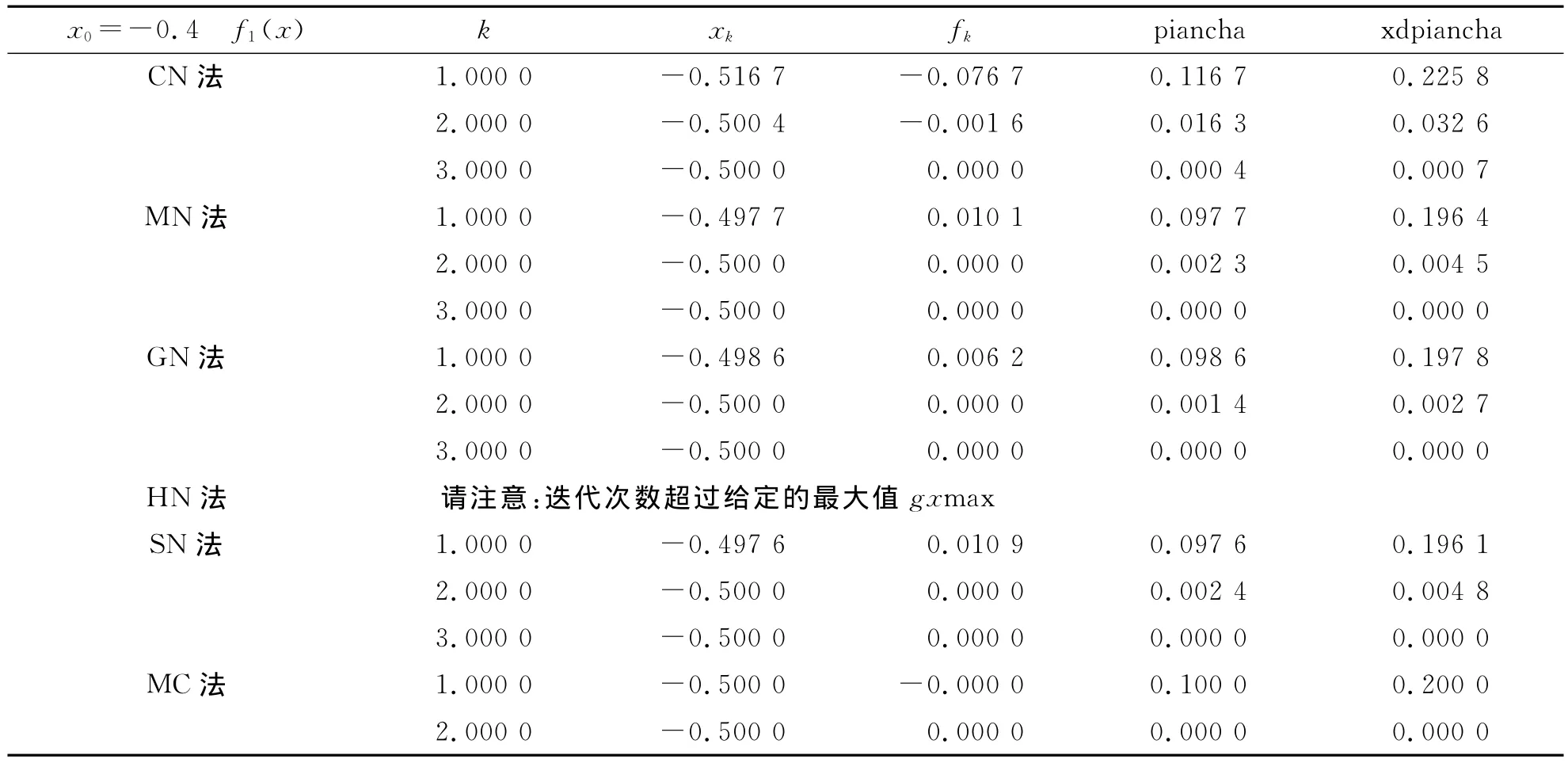
表1 五阶牛顿变形方法（MC）与几类牛顿改进格式的比较（f1（x）＝2x3－3x2＋1）Tab．1 Comparison of MC and several existing Newton improving formats（f1（x）＝2x3－3x2＋1）

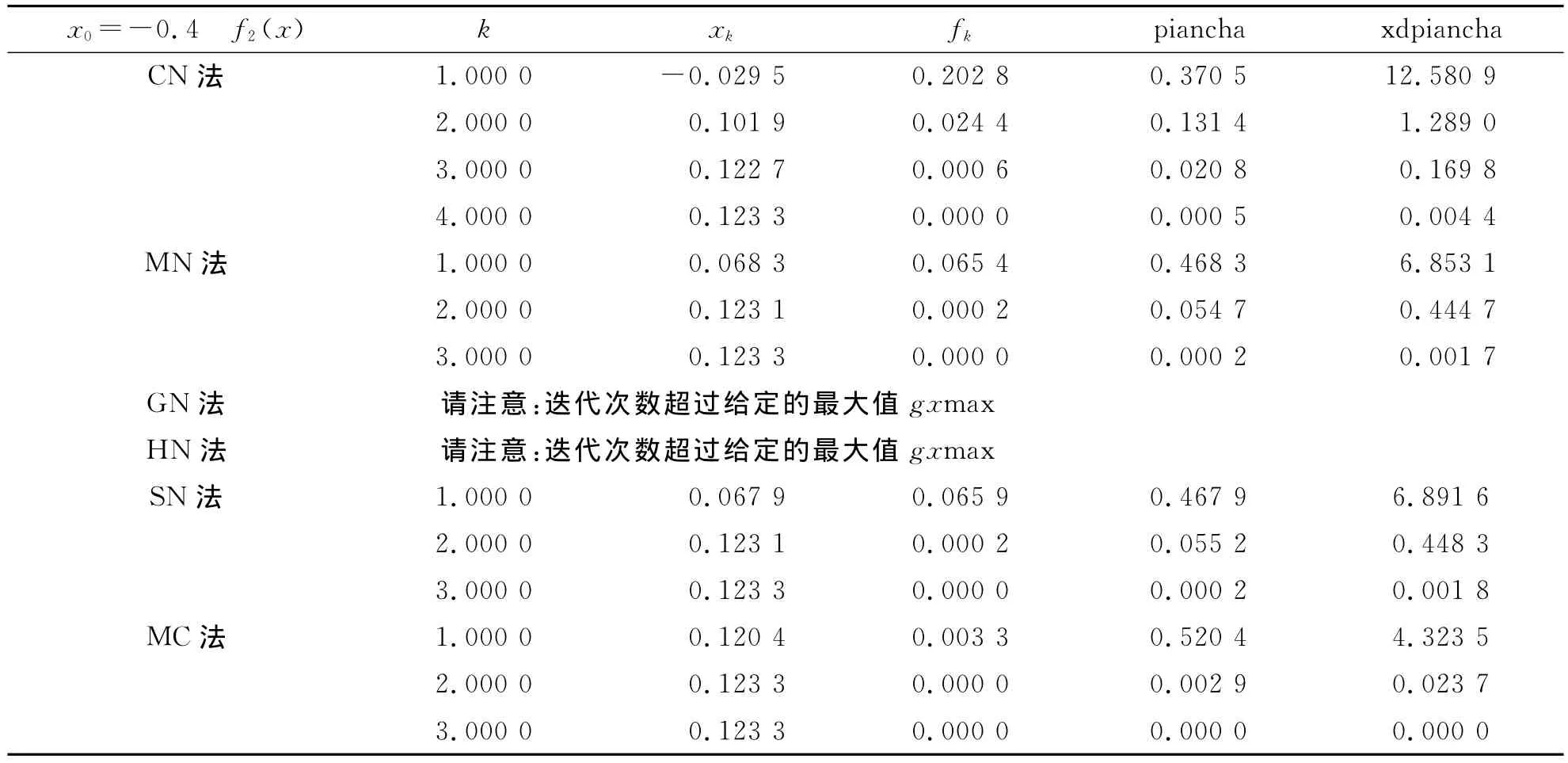
表2 五阶牛顿变形方法（MC）与几类牛顿改进格式的比较（f2（x）＝sin（x－1）＋（x－1）2）Tab．2 Comparison of MC and several existing Newton improving formats（f2（x）＝sin（x－1）＋（x－1）2）

表3 五阶牛顿变形方法（MC）与几类牛顿改进格式的比较（f3（x）＝4x4＋5x2）Tab．3 Comparison of MC and several existing Newton improving formats（f3（x）＝4x4＋5x2）

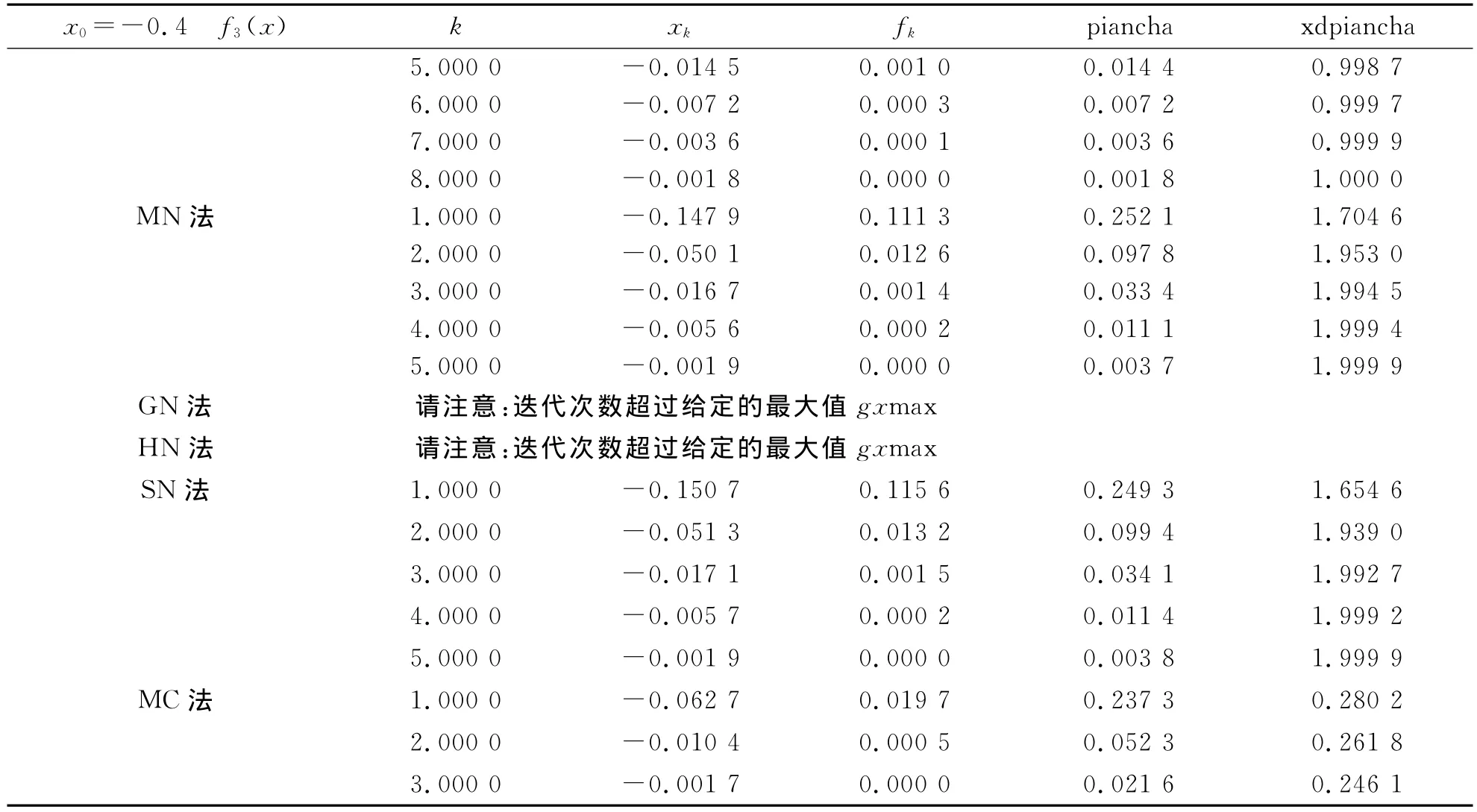
续表

上述数据显示，五阶牛顿变形方法（MC）的精度及收敛速度都优于经典牛顿法（CN）、中点牛顿法（MN）、几何平均牛顿法（GN）、调和平均牛顿法（HN）和Simpson牛顿法（SN）．

［1］莫小平．中点牛顿迭代格式的最优性［J］．数学的实践与认识，2009，39（13）：228－231．

［2］王霞，赵玲玲，李飞敏．牛顿方法的两个新格式［J］．数学的实践与认识，2007，37（1）：72－76．

［3］于明明，吴开谡，张妍．牛顿迭代法与几种改进格式的效率指数［J］．数学的实践与认识，2008，38（18）：154－159．

［4］田秋菊，宋岱才．Newton迭代法的一种新改进［J］．科学技术与工程，2011，11（3）：558－560．

［5］王晓峰．一种修正的牛顿迭代法［J］．长春理工大学学报：自然科学版，2010，33（1）：178－179．

［6］张荣，薛国民．修正的三次收敛的牛顿迭代法［J］．大学数学，2005，21（1）：80－82．

［7］柳辉．解非线性方程的牛顿迭代法及其应用［J］．重庆工学院学报：自然科学版，2007，21（8）：95－98．

［8］郑权．牛顿法的一点注记和改进［J］．北方工业大学学报，2002，14（3）：21－24．

［9］Chun C．Iterative methods improving Newton's method by the decomposition method［J］．Comput Math Appl，2005，50（22）：1559－1568．

［10］Golbabai A，Javidi M．Newton－like iterative methods for solving system of non－liner equations［J］．Appl Math Comput，2007，192（35）：546－551．

Abstract：Based on the classical Newton's method and the midpoint Newton's method，the paper presented a new fifthorder convergent iterative algorithm and its acceleration formula for nonlinear equations．Results of the numerical experiments show that the proposed algorithm is more accurate and efficient than the classical Newton's method and several existing Newton improving formats，such as Midpoint Newton's method，Geometrical mean Newton's method，Harmonic mean Newton's method and Simpson Newton's method．

Key words：nonlinear equation；degree of convergence；numerical experiments；iterative method

A Class of Fifth－Order Convergence Variants of Newton's Method and Its Acceleration

ZHOU Ren－feng，CAI Jing
（School of Science，Huzhou Teachers College，Huzhou 313000，China）

O241．7 MSC2010：65H99

A

1674－232X（2011）06－0529－06

10．3969／j．issn．1674－232X．2011．06．011

2011－05－28

浙江省自然科学基金项目（Y6110043）；湖州市自然科学基金项目（2010YZ05）；国家特色专业建设点项目．

周任沣（1987—），女，浙江宁波人，信息与计算科学专业本科生，主要从事计算数学研究．

＊通信作者：蔡 静（1975—），女，浙江湖州人，副教授，主要从事计算数学研究．E－mail：caijing＠hutc．zj．cn