赋范线性空间中有限簇渐近一致Φ－伪压缩映象的不动点迭代逼近

阿力非日，张 艳

（1.四川省岳池县第一中学，四川广安638300；2.西华师范大学数学与信息学院，四川南充637002）

赋范线性空间中有限簇渐近一致Φ－伪压缩映象的不动点迭代逼近

阿力非日1，2，张 艳2

（1.四川省岳池县第一中学，四川广安638300；2.西华师范大学数学与信息学院，四川南充637002）

文章在赋范线性空间中研究了有限簇渐近一致Φ－伪压缩映象具有误差的隐迭代序列的收敛性问题，得到了更一般的结论，改进和推广了相应的结果.

渐近一致Φ－伪压缩映象；赋范空间；迭代程序；不动点

1 引言及预备知识

2006年，谷峰教授研究了赋范空间中渐近一致Φ－伪压缩映象的迭代逼近问题［1］.即设D是赋范空间X中的非空凸子集，若序列｛xn｝迭代定义为：

定义1 设D是X的一个非空子集，T：D→D是一个映象.Φ：［0，＋∞）→［0，＋∞）是一严格递增的函数，且Φ（0）＝0.

1）T称为渐近伪压缩的.如果存在一实数列｛rn｝⊂［1，＋∞），lim rn＝1，而且对∀x，y∈D，∃j（x－y）∈使得

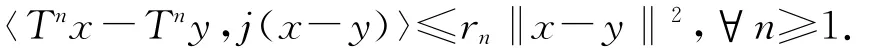
2）T称为渐近Φ－伪压缩的.如果存在x＊∈D，使得对∀x∈D，∃j（x－x＊）∈J（x－x＊），有

其中T：D→D是渐近一致Φ－伪压缩的一致L－lipschitz映象，则在一定条件下，｛xn｝强收敛于x＊.特别，如果q∈D是T的不动点，则xn→q（n→∞）.受其影响，该文将单个渐近一致Φ－伪压缩映象的结果推广到有限个的结果.

为证明该文的结果，需要以下定义与引理.

文中处处设X是以实赋范线性空间.X＊是X的对偶空间，〈·，·〉表示X＊和X间的配对.映象J：X→2X＊是有下式定义的正规对偶映象：

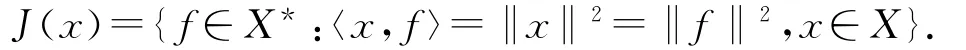
2 主要结果

定理1 设D是赋范空间X的一个非空凸子集，Tm：D→D（m＝1，2，…，N）是渐近一致Φ－伪压缩映象.具有常数rm，n的渐近伪压缩映射，且｛rm，n｝⊂［1，＋∞），lim rm，n＝1，F＝∩NF（Tm）不为空集，其中

n→∞m＝1F（Tm）为Tm的不动点集，那么：

i）如果q∈D是映象簇｛Tm｝mN＝1的任一不动点，则q＝x＊.从而映象簇｛Tm｝mN＝1至多只有一个不动点.

ii）对于∀x0∈D，序列｛xn｝n≥1如下定义：

函数Φ：［0，＋∞）→［0，＋∞），Φ（0）＝0，使得对x＊∈F，有

那么｛xn｝n≥1是有界的.

证明 i）不妨设存在异于x＊的不动点p∈D，即Tm（p）＝p（m＝1，2，3，…），则存在j（p－x＊）∈J（p－x＊），使得

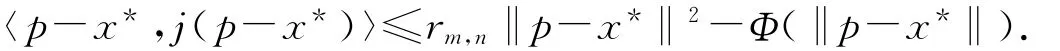
因为j是正规对偶映象，故有〈p－x＊，j（p－x＊）〉＝‖p－x＊‖2，从而

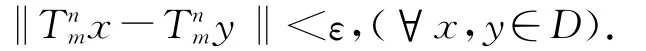
下面用数学归纳法证明｛xn｝是有界的.事实上，对任意的n≥0，‖xn－x＊‖≤2a.

当n＝0时，根据a的定义a＝sup｛k∈R＋：Φ（k）≤‖Tnm00xn0‖｝，有Φ（‖x0－x＊‖）≤‖Tnm00xn0‖.从而‖x0－x＊‖＜a＜2a.假设当n＝k时，‖xk－x＊‖≤2a成立.下证‖xk＋1－x＊‖≤2a.若不然，设‖xk＋1－x＊‖＞2a，则由Φ的严格递增性，有Φ（‖xk＋1－x＊‖）＞Φ（2a），又

注 该文将最近一些文献如［3］中的Banach空间推广到了赋范线性空间中，并去掉了定义域有界性的假设和空间光滑性的限制，同时将单个渐近一致Φ－伪压缩的收敛性推广到了有限个的结果，因此改进和推广了以前的相关结果.

［1］谷峰.赋范空间中渐进一致Φ－伪压缩型映象不动点的迭代逼近［J］.数学的实践与认识，2006，36（3）：281－287.

［2］Zhou H Y，Cho Y J.Ishikawa and Mann iterative processes with errors for nonlinearφ－strongly quasi－accretive mappings in nonmed linear spaces［J］.J Korean Math Soc，1999，36（6）：1061－1073.

［3］王丽萍，肖卓峰.有限个渐近伪压缩映射近迫点序列的收敛性［J］.数学的实践与认识，2010，40（3）：145－150.

The Iterative Approximation for Fixed Points of a Finite Family of Asymptotically IdenticalΦ－Pseudocontractive Mappings in Normed Linear Space

A Li Fei－ri1，2，ZHANG Yan2
（1.Yuechi No.1 Middle School，Guang'an 638300，China；2.School of Mathematics and Information，China West Normal University，Nanchong 637009，China）

The paper studied the convergence problems of iterative processes with errors under a finite family of asymptotically identicalΦ－pseudocontractive mappings in normed linear space，and obtained certain results which have improved and extended the corresponding results.

asymptotically identicalΦ－pseudocontractive mapping；normed space；iterative process；fixed point

0177.91 MSC2010：46B17；46T07

A

1674－232X（2011）06－0539－04

10.3969／j.issn.1674－232X.2011.06.013

2011－03－04

四川省教育厅重点课题基金项目（07ZA123）.

阿力非日（1986—），男，四川凉山人，应用数学专业硕士研究生，主要从事非线性分析研究.E－mail：yanxiaomeialfr＠163.com