基于FVCOM模式钱塘江河口涌潮三维数值模拟研究

谢东风,潘存鸿,吴修广

(浙江省水利河口研究院,浙江 杭州 310020)

基于FVCOM模式钱塘江河口涌潮三维数值模拟研究

谢东风,潘存鸿,吴修广

(浙江省水利河口研究院,浙江 杭州 310020)

应用FVCOM模型进行钱塘江涌潮的二维和三维数值模拟,并使用2007年10月大潮期间的现场观测结果进行模型验证。结果表明,平面二维模拟结果与实测值吻合较好,与基于Godunov算法求解钱塘江涌潮二维特征的结果基本一致。三维计算结果再现了流速在垂向上的差异,以及在落潮转向涨潮时刻,涨潮先从底部开始,垂向上从底层向表层逐步从落潮流转为涨潮流。敏感性分析显示模型网格大小和曼宁系数的选取对模拟结果有较大的影响。

钱塘江;涌潮;数值模拟;FVCOM

Abstract:In this contribution,the FVCOM model has been used to simulate the tidal bore in the Qiantang River.The depth-averaged 2-D model results agreewellwith the field data,which is consistentwith the research of Pan et al.(2007),who used a depth-averaged 2-D numericalmodel based on a Godunov-type scheme.The 3-Dmodel reproduced the vertical distribution characteristicsof current velocitiesand the physical processes,and the phenomenon thatwhen the ebb currents turn to flood currents,velocitiesat bottom increase first.Numerical experiments revealed that the cell size andmanning coefficient could influence themodel results to a large extent.

Key words:Qiantang River;tidal bore;numericalmodeling;FVCOM

涌潮是一种特殊的自由面重力流动,水流穿越涌波,水位、流速急剧变化。强涌潮是世界罕见的自然景观之一,世界上许多强潮河口都存在涌潮,如英国的塞文河、巴西的亚马逊河、长江口北支等。钱塘江涌潮以凶猛、多变、惊险而堪称一绝,从古至今吸引不计其数的观潮者。涌潮是一种罕见的自然景观,其巨大能量对河口过程有重要的影响,也影响到航运和河口生态系统。近年来在钱塘江河口治江围缩窄、建桥等人类活动对涌潮的影响以及涌潮的水力学结构方面进行了大量研究[1-2]。在其他河口,如长江口北支涌潮的形成及其影响因素亦取得了较大进展[3]。

东海潮波进入杭州湾后,潮差急速增大,传至湾顶澉浦,潮差与水深的比值已在2倍以上。受浅水效应影响,潮波非线性变形加剧,在澉浦上游形成水位骤然升高的涨潮波前锋线,即为涌潮。涌潮形成之初,潮后的潮位仍在上涨,因此强度逐渐增大,直到涌潮成为整个涨潮面,潮后潮位随即下降,涌潮较强时,分裂成前、后两股,逐渐减弱,直到湮灭[4]。与普通的潮波传播相比,涌潮前后存在水位、流速的突变,是典型的浅水间断流动,比潮波尺度要小好几个量级,因而给物理模拟和数值模拟都造成相当大的困难。从20世纪60年代开始,就有学者使用激波装配法和激波捕捉法探索钱塘江河口涌潮的一维或平面二维数值模拟[5-9]。2001年以来,潘存鸿等[10-15]提出了水位床底法同时结合底坡源项离散技术,建立了四边形网格和三角形网格下二维涌潮数值模型的Godunov格式和KFVS格式(kinetic flux vector splitting)。数值模拟给出精细的流速场,弥补了因测量困难,对流速分布状况知之不多的缺憾。然而,到目前为止,还没有对钱塘江涌潮进行三维数值模拟研究的报道。尝试使用现今国际上最新的河口、陆架和海洋模型FVCOM进行钱塘江河口涌潮的三维数值模拟,加深对钱塘江河口涌潮传播特性的认识。

1 模型建立与资料搜集

FVCOM模型为美国MassachusettsDartmouth州立大学陈长胜所领导的研究小组开发[16],其控制方程类似于POM模型,包括自由表面、非线性平流项、耦合的密度和速度场、径流、垂直混合的2.5阶湍流闭合模型等,数值模型采用有限体积法,可应用于各种河口、海湾、陆架和海洋问题。FVCOM模型采用σ垂向坐标和水平三角形非结构网格坐标的结合,可以使模型应用对感兴趣区域处的网格进行加密处理,既可控制计算量,又不牺牲笛卡尔坐标的特性。FVCOM采用类似POM的外模、内模分裂的模型求解。二维外模数值格式为基于三角形网格的有限体积法,将连续方程、动量方程在三角形区域积分后,通过改进的四阶龙格-库塔法求解。三维内模的动量方程求解采用简单的显式和隐式相结合的差分格式求解,其中流速的局部变换采用一阶精度的迎风格式,对流项采用二阶精度的改进龙格-库塔时间推进格式,垂向扩散则用隐式求解。此外,对于潮间带的处理,FVCOM引入了干/湿网格技术。

2007年10月大潮期间,组织了一次大规模钱塘江涌潮观测,上游富春江电站、下游澉浦断面。观测期间设置了20个潮位站,本研究范围内有11个(见图1),无涌潮时每小时记录一次潮位数据,涌潮到达后每1～2分钟记录一次数据。使用ADP进行流速观测,设置7个观测站位,本研究范围内有3个测站,它们是703站、705站、709站(图1),每个站位使用6点法进行观测,即分别位于水面、0.2倍水深、0.4倍水深、0.6倍水深、0.8倍水深和海底。无涌潮时,每小时记录一次流速数据,涌潮到达前后每分钟记录一次流速数据。观测期间最高潮位6.05 m,最高平均高潮位5.41 m,出现在仓前测站;最低潮位-3.50 m,最低平均低潮位-3.07m,出现于盖北中沙临时站。涨潮历时向西逐渐缩短,相应落潮历时延长。在闻家堰以下河段,平均涨、落潮历时差约3小时,至杭州段,平均涨潮历时只有约1小时,而平均落潮历时长达11小时以上。实测最大测点涨潮流速5.83m/s,出现在709测点表层,最大落潮流速3.84m/s,出现在709测点0.2倍水深层。最大涨、落潮流速在垂向上一般自表层向底层逐渐减弱,即表层最大,中层次之,底层最弱。通过观测,对钱塘江涌潮传播、发展规律有了进一步认识,同时也为数值模拟研究提供了详尽的资料。

图1 钱塘江河口Fig.1 Qiantang Estuary

计算范围从澉浦至仓前的72 km范围,河宽从澉浦站20 km缩窄到上边界仓前2 km(图1),进行岸边界平滑处理以后,使用无结构网格离散计算域,模型由17 409个节点和32 298个三角形单元组成,平均网格大小约300m,单元最小边长60 m,内外模的时间步长分别取10 s和2 s。地形数据使用2007年10月地形数值化以后插值得到,垂向上分7个等距的σ层。曼宁系数涨潮期间取值范围为0.004～0.01,落潮期间取值范围为0.007～0.02。模型海面边界对应风应力,海底边界条件对动量方程为引入底摩擦应力,对物质输运方程为垂向无通量。上下游开边界采用实测潮位数据。在模型验证与分析的基础上,通过数值试验对网格大小和曼宁系数对涌潮计算的影响进行敏感性分析。

2 模型验证与应用

2.1 潮位验证与平面二维模型计算结果

验证计算模拟了钱塘江涌潮形成、发展、及其衰减的过程,限于篇幅,文中绘出了2007年10月16～17日盐官、大缺口、曹娥江口三站的潮位验证过程,示于图2。由图可知,潮位的验证情况较好,高低潮位、潮差和位相均与实际吻合。当涌潮到达时水位上涨很快,这一跳跃现象在模型中被复演(图3),说明FVCOM模型能够捕捉到涌潮前后的水位间断特征。在计算域内,涌潮逐渐形成,并向上游逐渐增强,这一现象在模型中清楚地被重现。在下游曹娥江口段,当涨潮锋面到达时水位升幅数厘米。当涌潮到达盐官站时,涌潮高度达到最大,之后逐渐衰减,涌潮高度逐渐降低。

图2 潮位验证Fig.2 Tidal level validations

平面二维模型模拟结果与实际情况较为吻合,703、705、709三站涨落潮的最大计算流速及流速过程线与实测接近,受篇幅限制,这里不展示流速验证结果。落潮垂线平均流速大小在1～2 m/s之间,但是在涌潮到达以后涨潮垂向平均流速可以达到4～5 m/s。总体上看,垂向平均的最大流速向上游逐渐减小,三个站位的最大涨潮垂向平均流速分别为 5.0、4.0、3.7 m/s。涌潮传播过程中在平面上呈现一些特殊形态,习称“潮景”,数值计算再现了部分“潮景”,如交叉潮、一线潮、回头潮。总体上,潮位、流速、潮景的二维计算结果与基于Godnov格式和KFVS格式的二维数值模型[11-12]的计算结果基本一致。

2.2 三维模型计算结果

图4为709站表、中、底三层流速流向计算验证情况。结果表明,中层流速与实际情况吻合较好,表层流速与实际相比略小,而底层流速比实测值略大。尽管三维计算结果能够反映表层流速最大,中层次之,底层流速最小的流速向下递减的分布特征,但是各层差异不如实际情况明显。表层涨落潮最大流速实测值分别为5.51m/s和2.89m/s,计算值则分别为4.98m/s和1.97m/s,底层涨落潮最大流速实测值分别为3.56m/s和1.74 m/s,计算值则分别为4.40 m/s和1.37 m/s。

涌潮的三维特性与二维特性的主要差异表现为流速在垂线上瞬时分布上的不同。二维在垂线上均匀,三维在垂线上是变化的。在转流过程中先是底部增大,垂线上逐步过渡为满足对数分布。数值模拟结果复演了这一过程。图5展示709站在从落潮到涨潮的转流过程各σ层垂向流速分布。转流过程的垂线变化一方面是由水质点运动的惯性引起的,即落潮时期表层流速大,因而克服惯性慢,底层流速小,易于克服惯性,另一方面是由于下游盐度密度较大引起的。

为分析垂向流速分布的影响因素,从网格粗细和糙率系数两个方面进行了敏感性数值试验。通常,计算区域网格大小的选取取决于模型计算工作量和对计算结果精度的要求。由于涌潮流速时空分布的不均匀性,大流速可能只出现某一局部区域,且大流速出现的时间有先后。因此,较粗的计算网格难以捕捉到大的涌潮流速。上述模型的网格大小约300m,在此基础上将709站附近的局部区域网格加密到70m左右,其他参数保持不变。结果表明,网格加密以后,709站的涨落潮最大流速分别增加了2 m/s和0.5 m/s左右(图 6)。

图3 盐官涌潮到达前后潮位的实测值与计算值Fig.3 Observed and calculated tidal levels at Yanguan when the bore arrives

底床糙率系数是模拟潮流运动的一个重要参数,但是在现场很难对糙率系数进行直接观测,因此糙率系数是在数值模拟中初始条件和边界条件都较为准确的情况下进行模型校正的一个重要方式[17]。本模型使用曼宁系数表示糙率,涨潮和落潮阶段的曼宁系数分别取0.004～0.01和0.007～0.02,这种情况下,流速的垂向差异并不明显。在不改变其他参数的前提下,将涨落潮曼宁系数增大至0.01～0.02。结果显示。随着曼宁系数的增大,各层的垂向流速都有所减小,涨潮流速从4.40～4.98m/s减小为1.40～2.30 m/s,落潮流速从1.37～1.97 m/s减小为0.96～1.55 m/s。各层流速大小的差异则有所增加,表底层涨落潮流速的差异从12%和30%分别增大到39%和38%(表1)。说明曼宁系数能够在较大程度上影响流速的垂向分布特征。

图4 709站流速流向验证Fig.4 Comparison of computed andmeasured three-dimensional velocities at 709

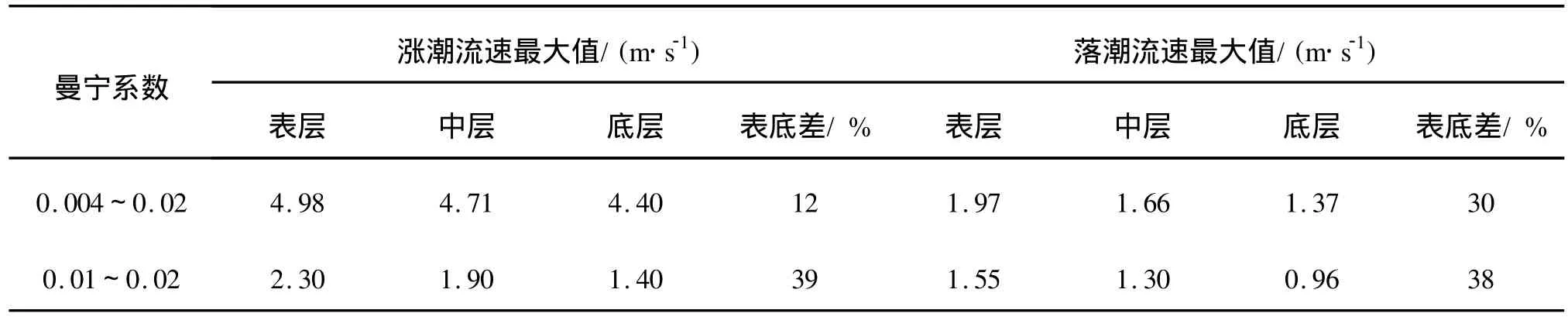
表1 不同曼宁系数取值下709站表、中、底层涨落潮流速最大值Tab.1 Maximal flood and ebb velocitiesat surface,m iddle and bottom of 709 with differentmanning coefficients

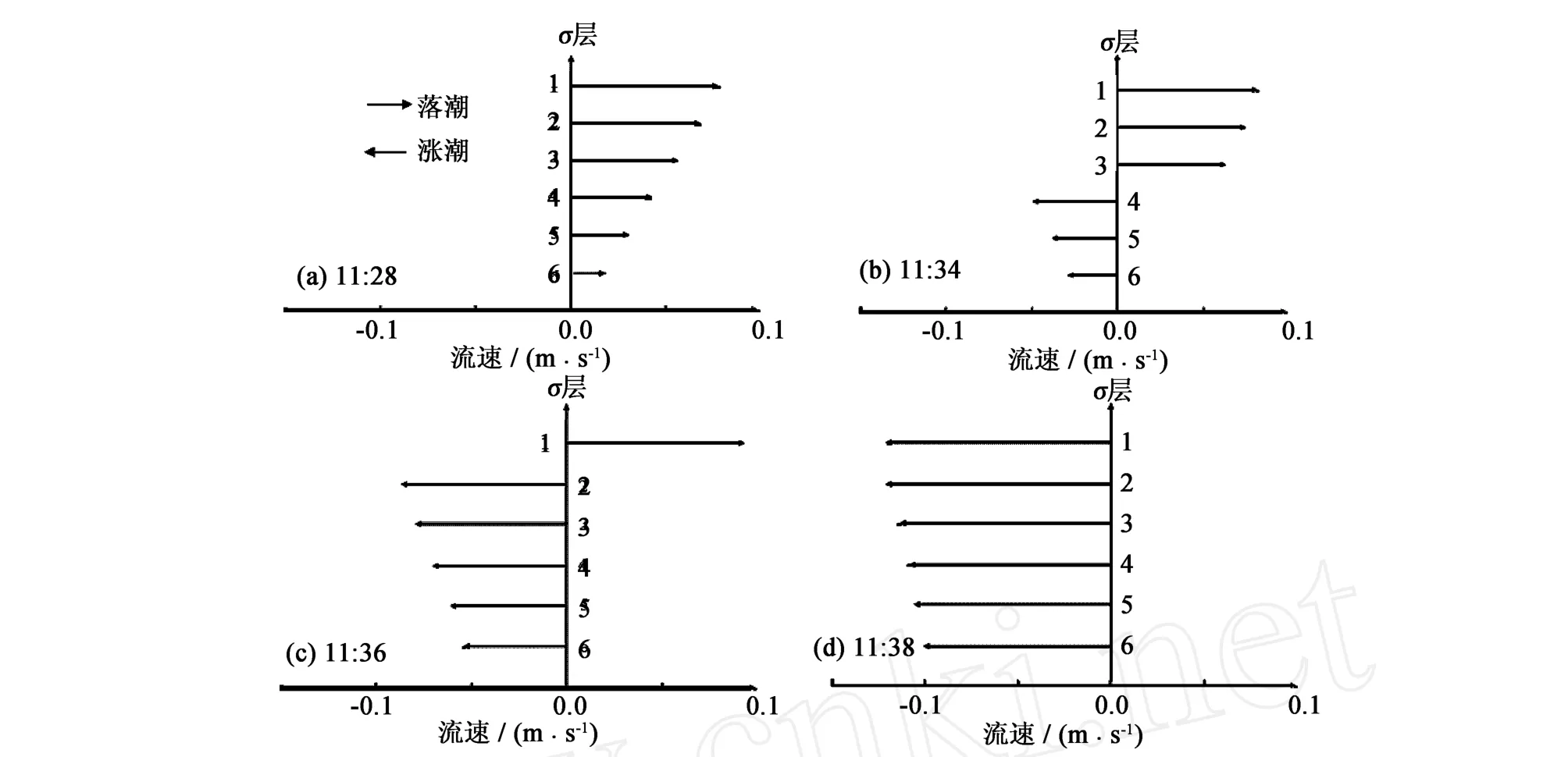
图5 709站落潮到涨潮的转流过程各层流速分布Fig.5 Current velocities atσlayerswhen ebb currents turn to flood currents at 709

图6 709站模型加密前后流速-时间曲线Fig.6 Depth-averaged velocity vs.time at 709

3 结 语

使用FVCOM模型进行了钱塘江河口涌潮的三维数值模拟,结果表明FVCOM可以捕捉到涌潮到达时的流速和水位突变过程。当选用较小的曼宁系数时可以使平面二维模拟结果与实测数据吻合良好,典型的潮景被再现,这与前人基于Godunov和KFVS格式的平面二维数值模拟结果基本一致。三维计算再现了流速在垂向上的差异,即表层最大、中层次之,底层最小。在落潮转向涨潮的过程中,先是底部流速增大,垂向上逐步过渡为满足对数分布。然而模型结果在各层流速的差异上不如实测数据明显。数值试验显示,模型网格粗细可以在较大程度上影响计算流速大小,当网格大小从300m加密到70 m,局部流速增大约1 m/s。在小的曼宁系数下,流速的垂向差异并不明显,仅在高潮位憩流期间各层流速差异较大。如果选用较大的曼宁系数,流速在垂向上的差异增大,但是流速减小。此外,为准确求解涌潮的传播速度,必须应用守恒型计算方法。数值实验表明[19],由于FVCOM的控制为非守恒型,涌潮的传播速度与时间步长有关。

涌潮是一种极为特殊的水流运动,流速大、水流特性复杂。钱塘江涌潮到达时,流速一般为6～7m/s,实测最大测点流速达12 m/s。前人计算结果表明,往往需要选用较小的糙率系数以使计算流速与实测流速吻合。然而,三维数值模拟结果显示,小的曼宁系数使得垂向流速分布不显著。其可能的原因是:水流运动方程中的阻力项采用谢才公式或修正形式,这种粗糙的处理使得原本定义明确的糙率系数变得包罗万象,相应地物理意义也变得极其含糊。因此,要较好地模拟涌潮作用下垂向流速的差异,很大程度上还有赖于糙率研究的进展。

[1] 鲁海燕,潘存鸿,卢祥兴,等.钱塘江海宁三期治江围涂工程对涌潮影响的数值模拟研究[J].水动力学研究与进展:A辑,2008,23(5):484-491.

[2] 杨火其,潘存鸿,周建炯,等.涌潮水力学特性试验研究[J].水电能源科学,2008,26(4):136-138.

[3] 陈沈良,谷国传,刘勇胜.长江口北支涌潮的形成条件及其初生地探讨[J].水利学报,2003(11):30-36.

[4] 林炳尧,黄世昌,毛献忠,等.钱塘江河口潮波变化过程[J].水动力学研究与进展:A辑,2002,17(6):665-675.

[5] 金旦华,刘国俊,周本华.一维涌潮计算[J].应用数学与计算数学,1965,3(2):183-195.

[6] 赵雪华.钱塘江涌潮的一维数学模型[J].水利学报,1985(1):50-54.

[7] 谭维炎,胡四一,韩曾萃,等.钱塘江涌潮的二维数值模拟[J].水科学进展,1995,6(2):83-93.

[8] 苏铭德,徐 昕,朱锦林.数值模拟在钱塘江涌潮分析中的应用-Ⅰ数值计算方法[J].力学学报,1999,31(5):521-533.

[9] 苏铭德,徐昕,朱锦林.数值模拟在钱塘江涌潮分析中的应用-Ⅱ计算结果分析[J].力学学报,1999,31(6):700-16.

[10] HuiW H,Pan CH.Water level-bottom topography for the shallow-water flow with application to the tidal boreson the Qiantang River[J].Computational and Dynamics Journal,2003,12(3):549-55.

[11] 潘存鸿,林炳尧,毛献忠.求解二维浅水流动方程的Godunov格式[J].水动力学研究与进展:A辑,2003,l8(1):16-23.

[12] 潘存鸿,徐 昆.三角形网格下求解二维浅水方程的 KFVS格式[J].水利学报,2006,37(7):858-864.

[13] 潘存鸿,林炳尧,毛献忠.钱塘江涌潮二维数值模拟[J].海洋工程,2007,25(1):50-56.

[14] 潘存鸿,鲁海燕,曾 剑.钱塘江涌潮特性及其数值模拟[J].水利水运工程学报,2008(2):1-9.

[15] Pan C H,Lin B Y,Mao X Z.Case study:Numericalmodeling of the tidal bore on the Qiantang River,China[J].Journal of Hydraulic Engineering,2007,133(2):130-138.

[16] Chen C,Liu H,Beardsley R.An unstructured grid,finite-volume,three-dimensional,primitive equationsoceanmodel:Application to coastal ocean and estuaries[J].Journal of Atmospheric and Oceanic Technology,2003,20(1):159-186.

[17] You ZJ.Estimation of bed roughness from mean velocitiesmeasured at two levels near the seabed[J].Continental Shelf Research,2005,25(9):1043-1051.

[18] 倪晋仁,薛 安,秦华鹏.影响水流运动研究进展的若干关键问题I.糙率研究[J].应用基础与工程科学学报,1997,5(4):371-380.

[19] 潘存鸿.浅水间断流动数值模拟研究进展[J].水利水电科技进展,2010,30(5):77-84.

Three-dimensional numericalmodeling of tidal bore in Qiantang based on FVCOM

XIEDong-feng,PAN Cun-hong,WU Xiu-guang
(Zhejiang Institute of Hydraulics and Estuary,Hangzhou 310020,China)

TV142

A

1005-9865(2011)01-0047-06

2010-04-08

国家自然科学基金资助项目(41006053,40806037,50809062);国家水体污染控制与治理科技重大专项(2009ZX07424-001);浙江省创新团队建设资助项目(2009F20024);水利部公益性行业科研专项经营资助项目(200801072)

谢东风(1981-),男,四川安岳人,博士,主要从事海洋沉积动力学研究。E-mail:eastwind111@hotmail.com