深水半潜式钻井平台动力定位最优作业方向研究

李勇跃,王 磊,孙 攀

(上海交通大学海洋工程国家重点实验室,上海 200240)

深水半潜式钻井平台动力定位最优作业方向研究

李勇跃,王 磊,孙 攀

(上海交通大学海洋工程国家重点实验室,上海 200240)

从动力定位的角度,以深水半潜式钻井平台为研究对象,对其在不同方向环境载荷作用下的动力定位进行时域模拟,得到作业工况各角度下平台水平方向位移以及功率消耗的时历。通过最优精度方向角和最优功率方向角的求解,最终得到平台的最优作业方向,满足海洋平台正常作业高精度、低能耗的要求,为平台的工程作业实践提供参考,并为模型实验提出新的研究方向。

动力定位;时域模拟;最优作业方向;钻井平台

Abstract:Based on dynamic positioning,time domain simulation of a semi-submersible platform′smotion induced by environment loads in different directions is done,from which time historiesof the displacementsand the consumed power in operation condition areobtained.In a further solution to the optimum precision angle and theoptimum power angle,theoptimum operation direction is finally determined,whichmeets the demand of high precision for someoperations.Thispaper offers some reference value to some engineering practices,such as the installation of the platform,and brings up a new topic formodal tests.

Key words:dynamic postioning;time domain simulation;optimum operation direction;drilling platform

动力定位技术是指船舶或其他浮式海洋结构物仅依靠自身推力器就能够自动保持其水平方向的位移和艏向[1]。对于深水作业的海洋平台,其相比传统的锚泊技术具有无法比拟的优势。目前,国际上的第六代半潜平台均采用动力定位技术[2]。

动力定位旨在以最小的能耗满足定位精度要求,以使得平台能够完成正常的作业。由于深海工程作业的复杂性,深水半潜式钻井平台的正常作业要求动力定位能够实现较高的精度,这样,寻求动力定位最优精度实现的条件成为工程中十分重要的问题。动力定位的精度取决于平台本身的特性、动力定位系统的性能以及海洋环境条件的特征,对一已知的海洋平台和给定的动力定位系统,海洋环境条件将成为影响动力定位精度的首要因素。在某一海域的不同时间段内,平台作业的环境载荷方向是变化的,从而使得平台的外干扰力发生变化,进而导致动力定位的精度出现变化,其结果是平台可能因精度不足而无法进行正常的作业。寻求平台最优精度方向,当平台在环境载荷方向发生变化时,即刻通过动力定位系统实现相应的变化,使得平台始终处于最优精度方向,以保证平台正常作业的顺利进行。另外,综合考虑精度和功率消耗,若在某一方向两者的组合达到最优,则该方向为平台的最优作业方向。根据不同的作业要求,始终保持平台于最优精度方向或最优作业方向,可有利于极大地提高平台深水作业的安全性和经济性。

以深水半潜平台为对象,介绍动力定位的基本原理,并对作业工况下的平台在各方向环境载荷作用下的运动进行时域模拟,寻求平台的最优作业方向。

1 计算模型

1.1 半潜平台模型

计算所用模型为一深水半潜式平台模型。平台的主要参数如表1所示。

表1 半潜平台模型主要参数Tab.1 Main parameters of the sem i-submersible platform

1.2 推力器模型

计算所采用的推力器模型为8个全方位推进器,螺旋桨直径为3.6m,四个安装在下浮体的外侧,四个在内侧,且相互于纵横中心线对称。内侧螺旋桨距离横纵中心线的距离分别为43.36 m和23.79 m,外侧螺旋桨距离横纵中心线的距离分别为43.36m和34.77m。

1.3 计算工况

为区别于以往对海洋平台进行动力定位能力分析所采用的设计海况[3],计算所用工况为平台的正常作业工况。由于风、浪、流同向为最恶劣的环境条件,取风、浪、流同向联合作用作为计算的环境条件,其参数如表2。

表2 平台作业状态环境条件Tab.2 The environment condition of the platform in operation case

计算中设计水深为3 000m。

1.4 计算坐标系

图1为计算使用的坐标系统。

2 平台时域模拟方法

动力定位的时域模拟又称为动态模拟,就是对在动力定位控制下的半潜式平台真实运动进行实时模拟,对运动状态作时域模拟能顾及到更多因素和限制条件,从而能较接近实际情况,同时获得许多有价值的信息,如动力定位精度、功率消耗等[4-6]。

深水半潜式平台动力定位运动模拟的流程如图2所示。主要的模块包括风浪流环境力的计算模型、控制系统模型、推力产生模型以及平台运动方程。其中环境载荷与平台的位置和运动状况有关,需要根据平台运动信息的反馈进行计算。控制系统也需要平台位置和运动信息的实时反馈以及风力前馈,以此计算出推力指令,推力系统则根据推力指令并结合推力器的特性模拟推力实时产生。环境力和推力提供了平台运动的外力,通过求解平台运动方程便可得到运动状态的时历。

这里仅给出平台运动的低频方程和推力系统中推力器功率的计算式。

图1 计算坐标系统Fig.1 coordinate system for computation

图2 半潜式平台动力定位运动模拟模型Fig.2 A model ofmotion simulation for DP semi-submersible platform

半潜式平台在外力作用下的低频运动方程:

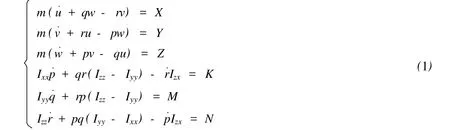
式中:u,v,w为线位移速度,即˙x,˙y,˙z(上点表示对时间的导数);p,q,r为角位移速度,即φ·,˙θ,˙Ψ;m为平台质量,包含流体附加质量;Ixx,Iyy,Izz为质量惯性矩,也包括附加质量部分;X,Y,Z分别为x,y和z方向的外力;K,M,N分别为x,y和z方向的外力矩。

推力器功率的计算公式:

式中:n为螺旋桨转速,Q为螺旋桨的转矩,D为螺旋桨的直径,KQ为转矩系数,KQ根据轴向进速在螺旋桨敞水性征曲线查取。

3 计算结果与分析

对平台动力定位过程进行时域模拟,计算时间取1 800 s,每24 s进行数据采集和记录,得到平台水平运动的时历。对环境载荷在0°～180°之间进行计算,每5°记录一次数据,并在每一角度下对各参数取时间的平均值,得到各角度下水平方向位移曲线,由于平台几何尺寸与环境载荷的对称性,同时计算结果显示,0°至90°与 90°至 180°区间数据基本对称 ,故这里展示区间仅为 0°至 90°区间。

3.1 动力定位的能力分析

这里计算平台能否满足定位的精度要求,是进行继续分析的前提。对平台时域模拟的位移时历进行统计,得到如图3所示的各方向角环境载荷作用下平台运动的最大位移。

对于钻探平台,钻井立管相对井口或其顶端连接处的允许偏离弯曲角度决定平台可偏移位置的大小。一般来说,该角度保持在2°范围内是趋于安全的,从图3(a)和(b)中可以看出,平台在各个方向的环境力作用下均能满足精度要求。对于艏向角的精度要求,目前还没有文献进行明确的规定,从最大艏向角的变化曲线可以看出,除在60°左右(约在62°时环境载荷最大)的最大艏向角大于4°外,其余艏向角均低于4°,认为艏向角也满足精度要求,从而平台在各个方向上都能够满足定位精度要求。

图3 平台在各个角度环境力作用下的最大位移Fig.3 Maximum displacementsof the platform affected by the environment forces in different directions

3.2 最优精度方向

最优精度方向,即在该方向下,平台能够满足动力定位的精度,且具有最高的精度。这里,将不再考虑平台最大的偏移量,而是用平均偏移量进行考察。

对于不同功能的海洋平台,或者对同一平台的不同作业,其对精度的要求有所不同。一般的钻井平台,其对水平方向的位移要求有较高的控制,而对艏向角的要求则较低。但对有些平台,其艏向角的控制也很重要。这里对这两种不同的情况,分别作不同的处理。

3.2.1 仅考虑水平位移的情况

图4 平台在各方向环境力作用下的平均位移Fig.4 Average displacementsof the platform affected by the environment forces in different directions

从图4中可以看出,x和y方向的平均位移的变化趋势是相反的。从图5中可以看出,标准差的变化趋势与位移的变化趋势一致。故综合考虑均值和标准差,平台x方向的最优精度出现在环境载荷为90°的情况,平台y方向的最优精度出现在环境载荷方向为0°的情况。考察R随载荷方向变化的情况,发现R在0°时取的最小值,由于通过x和y的标准差直接求取R的标准差比较困难,这里仍通过x和y的标准差来估算,综合R的变化趋势与x和y的标准差的变化趋势,平台的最优精度方向为0°。

3.2.2 考虑艏向角的情况

水深用l表示,取θ1=arctan(),令平均艏摇角为θ2,这里首先给出安全区的定义。

以θ1为横轴,θ2为竖轴,建立平面直角坐标系(如图7),任意一点P(θ1,θ2)代表动力定位精度,a,b分别为动力定位精度控制值,图中阴影部分(-a≤θ1≤a,-b≤θ2≤b)代表动力定位安全区,即满足精度要求的点的集合,安全区之外的点均不满足精度要求。

从上面的计算可以知道,平台在任何方向环境载荷作用下的动力定位均处于安全区,下面继续给出安全区内判定精度优劣的参数-动力定位精度角的定义。

不同的系统对于水平位移和艏向角的控制程度是不同的,这里引入控制因子v(0≤v≤1)来表示系统对角位移的控制程度。令

其中,-a≤θ1≤a,-b≤θ2≤b,称θdp为动力定位精度角。从其定义可以看出,θdp的值越小代表该工况下,动力定位的精度越高,可知θdp=0是最理想的情况(这里仅从精度方面考虑)。可知,3.2.1所讨论的情况为v=0的特例。

图5 平台在各方向环境力作用下的平均位移的标准差Fig.5 Standard deviation of the average displacementsof the platform in different directions

图6 平台在各方向环境力作用下的平均偏移距离Fig.6 The average drift distancesof the platform in different directions

图7 动力定位安全区示意Fig.7 The safe area of the platform in dynamic positioning

这里,考虑另外一种理想情况。假设系统对于线位移和角位移的控制是等同的,即v=0.5,此时θdp=(|θ1|+|θ2|),图8和图9分别给出了θdp以及θ2的标准差随角度变化的趋势。

图8 各方向环境力下的θdp值Fig.8 The value ofθdpin different directions

图9 各方向环境力下的θ2的标准差Fig.9 The standurd deviation ofθ2in different directions

从图8中θdp的变化趋势可以看出,θdp在0°和90°的时候取得最小值,综合考虑x、y以及θ2的方差的变化趋势,可以得出,当v=0.5时,最优精度方向为0°和90°。

3.3 最优功率方向

最优功率方向,即在该方向下,平台能够满足动力定位的精度,且具有最低的功耗。

通过对动力定位过程中消耗功率的时历统计,得到各方向环境力作用下螺旋桨消耗的总功率,如图10所示。

从图中可以清晰的看出,随着角度的增加,螺旋桨消耗的总功率几乎成线性增加,在0°方向时,功率消耗最小,故最优功率方向为0°。

3.4 基于动力定位能力分析的最优作业方向

这里首先给出最优作业方向的定义。

动力定位旨在满足定位精度要求的情况下,获得最小的功率消耗,因此,精度和能耗两方面的因素必须同时考虑。这里,用A表示精度值,B表示消耗的功率值,D表示动力定位能力值,且规定D值越大,动力定位能力越强。假设D为A和B的某种线性组合:

式中:α和β分别表示精度和功率消耗对平台作业的影响程度。A和B均为环境载荷方向角的函数,则上式变为

令θopt为最优作业方向角,则θopt为D(θ)取得最大值时的θ值。

由于精度和功率同时在0°时取得最优,故0°方向为最优作业方向。如果最优精度方向与最优功率方向不同,则需要确定α和β的值,然后进行计算。

图10 各方向环境力作用下螺旋桨消耗的功率Fig.10 The total consumed powerof the propellers in different directions

4 结 语

以一深水半潜平台为研究对象,对其动力定位进行时域模拟。首次定义并使用动力定位精度角作为衡量动力定位精度的参数。在其满足精度要求的条件下,求取了两种情况下的最优精度方向,并结合最优功率方向,最终得到该平台的最优作业方向。

在计算时,视平台为固定,环境载荷方向依次从0°变化到180°(由于其对称性,文章中仅给出0到90°区间的数据),最终得到0°方向为最优作业方向。在平台实际作业中,作业海域的环境载荷方向在不同的时间段内是发生变化的。从计算结果可以知道,通过动力定位系统,始终保持平台处于最优作业方向,可使平台的动力定位精度最高,能耗最小,从而能保证某些具有高精度要求的作业的顺利进行,提高了平台深水作业的安全性、可靠性和经济性。

[1] Jon Holvik,Kongsberg Simrad.Basicsof dynamic positioning[C]∥Dynamic Positioning Conference.1998.

[2] 栾 苏,韩成才,王维旭,等.半潜式海洋钻井平台的发展[J].石油矿产机械,2008,37(11):90-93.

[3] 赵志高,杨建民,王 磊,等.动力定位系统发展状况及研究方法[J].海洋工程,2002,20(1):91-97.

[4] MARIN.DPSEM I软件用手册[M].

[5] Ir F van Walree.MathematicalModel of DPSim:A Simulation Program for Dynamically Positioned Vessels[R].MARIN:47940-4-RD,1989.

[6] U Nienhuis.Simulationsof low frequencymotionsof dynamically positoned structures[C]∥RINA Spring Meeting.1986.

[7] Asgeir J Sorensen,Bernt Leira,Jann Peter Strand,et al.Optimalsetpoint chasing in dynamic positioningof deep-water drilling and intervention vessels[J].Int.J.Robust Nonlinear Control,2001,11:1187-1205(DOI:10.1002/rnc.602).

Research on the optimum operation direction for a deep sea semi-submersible drilling platform based on dynamic positioning

LIYong-yue,WANGLei,SUN Pan
(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

P751

A

1005-9865(2011)01-0026-06

2010-07-30

国家863重大项目课题“深水半潜式钻井船设计与建造关键技术”资助项目(2006AA09A104)

李勇跃(1988-),男,安徽淮北人,硕士生,主要从事动力定位研究。

王 磊。E-mail:wanglei@sjtu.edu.cn