关于二元函数极限的讨论

郭竹梅，高智中

(安徽科技学院 理学院，安徽 凤阳 233100)

关于二元函数极限的讨论

郭竹梅，高智中

(安徽科技学院 理学院，安徽 凤阳 233100)

二元函数求极限是高数中的难点；本文给出7种求二元函数极限的方法，并进一步给出极限一定不存在的3类二元函数．

二元函数；极限

极限理论是微积分学的基础，极限的思想方法在许多领域有着广泛的应用，二元函数的极限与一元函数的极限含义相同，它研究的是平面上动点趋向某一定点时，相应的函数值的变化趋势．根据二元函数极限的定义，在点P0(x0,y0)的邻域内，动点P(x,y)趋向于点P0(x0,y0)的方式是任意的．因此，在判定二元函数极限是否存在以及极限的计算上都有一定难度．文献[1]给出了一些求二元函数极限的方法，本文在完善求二元函数极限方法的同时，给出了极限一定不存在的3类二元函数．

1 二元函数极限的求法

1.1 利用二元函数的连续性

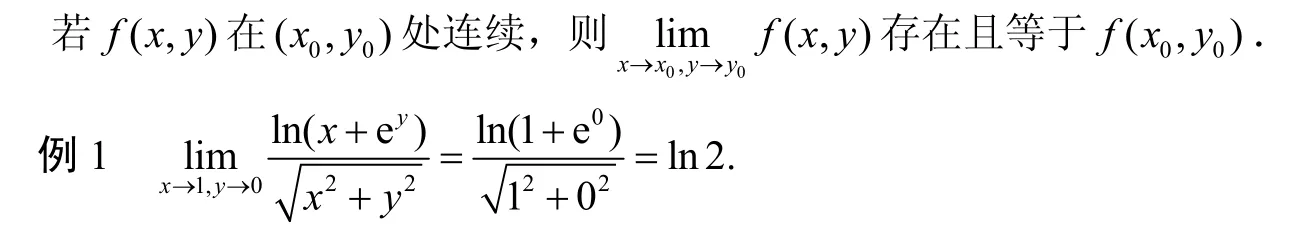
在例 7中，采用了代换x=rcosθ,y=rsinθ ．但实际上(x,y)→(0,0)与r→0并不等价．事实上(A是一常数)表明动点(x,y)沿着任一与轴正向夹角为的半直线趋向(0,0)时，f(x,y)无限接近于常数A，但这并不能说明(x,y)以任意方式趋向(0,0)时，f(x,y)也无限接近于常数A，即并不能保证等价于当r→0时，f(rcosθ ,rsinθ)在[0,2π]上一致收敛于常数A[3]．

众所周知，要证明二元函数的极限不存在，只要指出当动点以两种特殊方式趋于定点时，函数趋于2个不同的常数值；或者当动点以一种特殊方式趋于定点时，函数不趋于常数即可．下面指出3种极限一定不存在的二元函数．

2 极限不存在的3类二元函数

文中给出了几种常用的二元函数极限的求法，对于二元函数的极限还有利用二重积分的定义、洛必达法则、泰勒展开等方法[4-5]．对于具体题目要注意对上面几种方法的综合运用．

[1] 郭俊杰.二元函数求极限的方法[J].衡水学院学报,2006,8(1):15-16.

[2] 符兴安.二元函数极限计算方法研究[J].楚雄师范学院学报,2003,18(6):20-22.

[3] 殷乘元.二重极限的一致收敛判别法[J].高等数学研究, 2003,6(1):34-38.

[4] 陶会强,罗成广.二元函数极限的计算方法[J].天中学刊,2009,24(2):3-5.

[5] 陈明.泰勒公式在判定二元函数极限存在性中的应用[J].数学理论与应用,2004,24 (4):67-69.

Abstract:How to get the limit of bivariate function is a difficult point in advanced mathematics. Nowseven methods are provided in this article and three kindsof bivariate function are given, whose limits do not exist certainly.

Key words:bivariate function; limit

(责任编校：李建明英文校对：李玉玲）

Discussionabout the Limit of Bivariate Function

GUO Zhu-mei, GAO Zhi-zhong

(Institute of Science, Anhui Science and Technology University, Fengyang, Anhui 233100, China)

O13

A

1673-2065(2010)04-0017-03

2010-08-29

安徽科技学院校级课题资助项目(ZRC2008194)

郭竹梅(1980-),女,安徽淮北人,安徽科技学院理学院教师,理学硕士;

高智中(1979-),男,山西神池人,安徽科技学院理学院教师,理学硕士.