对改进隐枚举法的思考
程红萍,赵银锋
(1. 西安欧亚学院 数学教研室,陕西 西安 710065;2. 西门子信号有限公司,陕西 西安 710016)
对改进隐枚举法的思考
程红萍1,赵银锋2
(1. 西安欧亚学院 数学教研室,陕西 西安 710065;2. 西门子信号有限公司,陕西 西安 710016)
运用对比分析的研究方法,论证了隐枚举法在线性规划的 0-1整数规划解题的传统思路上可作改进,通过实例说明改进后的方法快捷可行.
0-1整数规划;隐枚举法;改进的隐枚举法
对于0-1型整数规划问题的一种求解方法,人们最容易想到的是穷举法,即检查变量取值为0或1的每一种组合,比较目标函数值以求得最优解,这就需要检查变量(n个)取值的 2n个组合.对于变量个数 n较大(例如 n>10)时,这几乎是不可能的.因此常设计一些方法,只检查变量取值的组合的一部分,就能求到问题的最优解.这样的方法称为隐枚举法.隐枚举法作为一种求解 0-1型整数规划问题的方法,它的产生极大地推动了经济管理、科学研究、工程技术等诸多领域的理论研究和实践运用发展.隐枚举法的基本思路是从所有变量等于零出发,依次指定一些变量为 1,直到得到一个可行解,并将它作为目前最好的可行解.此后,依次检查变量等于0或1的某些组合,以便使目前最好的可行解不断加以改进,最终获得最优解.隐枚举法不同于穷举法,它不需要将所有可行的变量组合一一列表.它通过分析、判断排除了许多变量组合作为最优解的可能性.
但在实际的运用中也常常会遇到这样的问题,所有变量从零出发,依次指定一些变量为 1,那么哪些变量取1呢?关于这方面,曾经有人改进过:如果目标函数为最大化,那么先试探让系数最大的变量 xj取1,其余变量都取 0;如果目标函数为最小化,那么先试探让系数最小的变量 xj取 1,其余变量都取 0;这样就可以减少运算次数.在教学与实践中本人也做了这方面的尝试,在尝试过程中发现虽然运算次数比以前少了,但相对来说,运算次数还是较多.因此,有必要对隐枚举法做进一步的改进.这既是一个解决实践运用问题的需要,也是一个急需解决的理论问题.本文拟就如何改进隐枚举法做以粗浅的探讨.
改进隐枚举法的观点或设想:正是因为隐枚举法的第一步是先通过试探的方法找到一个可行解的,那么根据它的这个特点,对于目标函数为最大化的,我们若从目标函数中 xj的系数为正的变量都取 1而其他变量都取0开始试探,就会发现下面的运算次数会大大减少;并且一般只需要几步就能找到最优解;而对于目标函数为最小化的,我们若从目标函数中 xj的系数为负的变量都取 1而其他变量都取 0开始试探,也会发现下面的运算次数会大大减少.
对于隐枚举法和改进隐枚举法异同即改进隐枚举法的优越性,我们可以通过对同一模型的求解来比较分析论证:
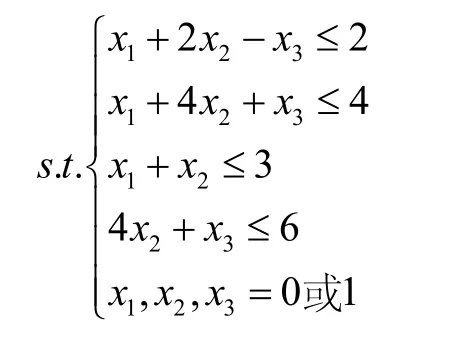
解 1) 运用隐枚举法来求解
第一步:先通过试探的方法找一个可行解,易看出X(0)=(x1,x2,x3)=(1,0,0)满足约束条件,故为一个可行解,且相应的目标函数值为z0=3.
第二步:因为是求极大值问题,故求最优解时,当然希望z≥3了,于是应增加一个约束条件(称该条件为过滤条件):3x1-2x2+53≥3,从而与原问题等价的新规划模型为:
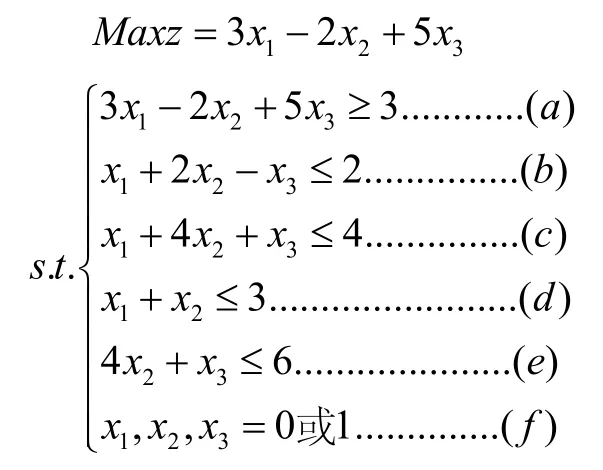
第三步:求解新的规划问题
3个变量共有8种可能的组合,我们将这8种组合依次检验它是否满足条件(a)~(e),对某个组合,若它不满足(a ),即不满足过滤条件,则(b)~(e)即可行性条件不必再检验;若它满足(a)~(e)且相应的目标值严格大于3,则进行第四步.
第四步:改进过滤条件直到找到最优解.
按上述思路与方法,例1的求解过程可由表1来表示:
从而得最优解X*=(x1,x2,x3)=(1,0,1),最优值z*=8.
2) 运用改进的隐枚举法来求解
我们仍以上述0-1规划模型为例来说明改进的隐枚举法求解的简便性.
第一步:因为目标函数中x1、x2的系数都大于零,因此先找一个可行解X(0)=(x,x,x)=(1,0,1),此时z0=8.
第二步:增加一个约束条件:3x1-2x2+53≥8,从而原问题等价于
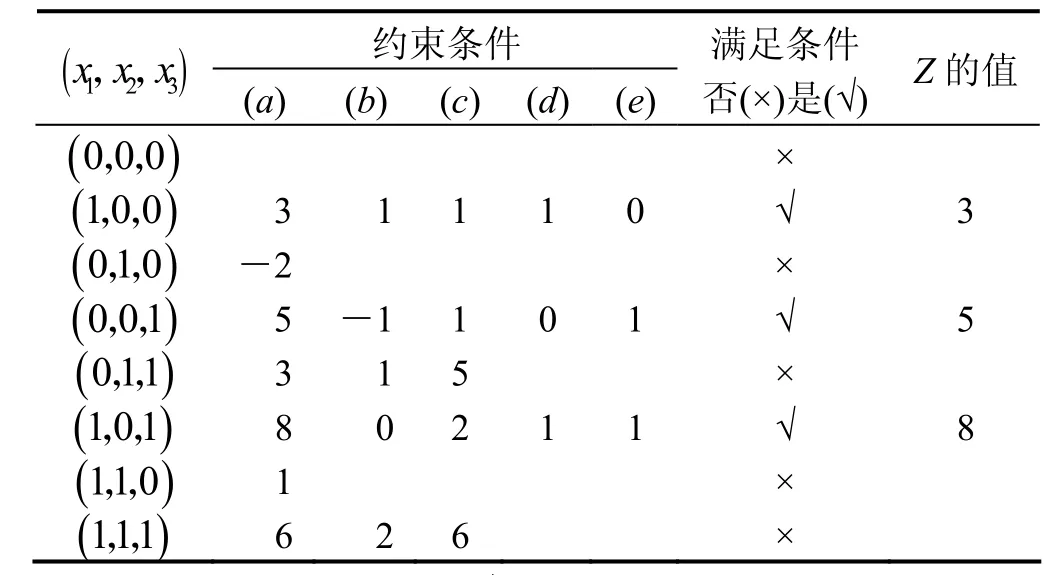
表1 改进前的判断过程
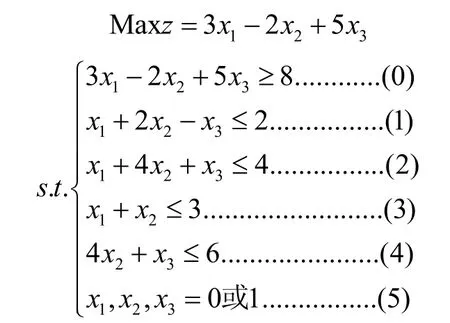
第三步:求解新的规划问题(和前面的第三步相同)
第四步:改进过滤条件直到找到最优解.
按上述思路与方法,例1的求解过程可由表2表示.
至此,z值已不能再改进.即得最优解:maxz=8,x*=(x1,x2,x3)=(1,0,1).
比较表 1与表 2,显然表 2的计算判断次数明显少于表1的计算判断次数,表2总共只计算判断了12次.而表1总共要计算判断24次.
通过实例分析比较,我们可以得出这样一个结论:隐枚举法和改进的隐枚举法在对同一个问题的求解中,解的结果是完全相同的.但是,改进的隐枚举法在实际运用中却凸现了比隐枚举法更加方便快捷的优越性,表现在:对隐枚举法的第一步进行改进,即对于目标函数为最大(小)化的,我们若从目标函数中xj的系数为正(负)的变量都取 1而其他变量都取 0开始试探,就会发现下面步骤的运算次数会大大减少,本文例 1使用了2种方法进行求解,大家明显可以看到使用改进的隐枚举法求解时确实大大地减少了运算次数,并且在运算次数大大减少的同时,还提高了运算的精确度.也体现了这种方法在推动实际工作实践中的有效性.
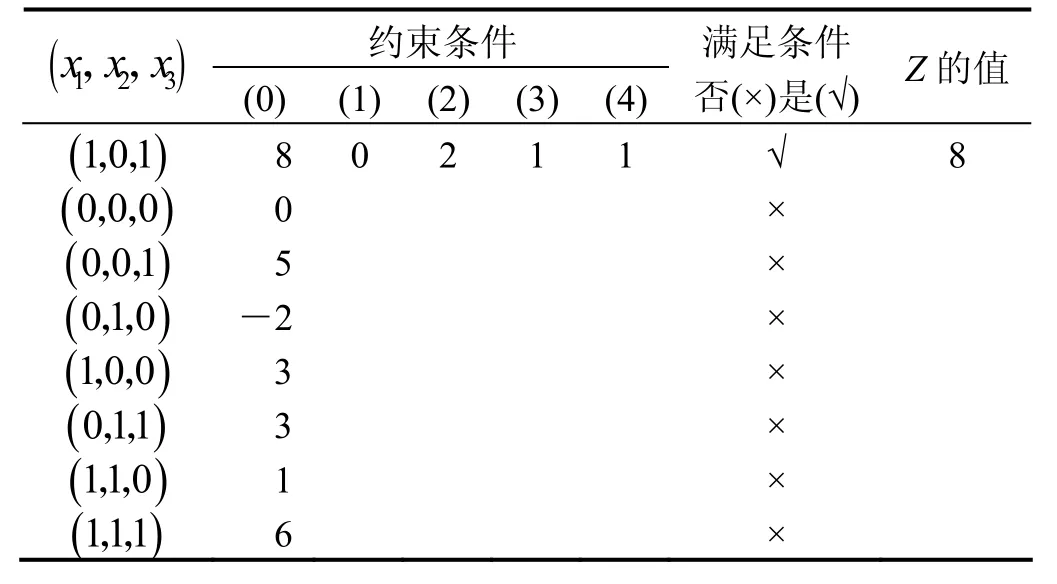
表2 改进后的判断过程
Abstract:This paper, from a perspective of contrastive analysis, has researched into the improvement of the Implicit Enumeration Method in applying the 0-1 Integer Programming in the Linear Programming. Practical examples have proved that the improved method is faster and feasible.
Key words:the 0-1 Integer Programming; the Implicit Enumeration Method; the improved enumeration
(责任编校:李建明英文校对:李玉玲)
Reflections on Improving the Implicit Enumeration Method
CHENG Hong-ping1; ZHAO Yin-feng2
(1. Teaching Office of Mathematics, Xi’an Eurasia University, Xi’an, Shaanxi 710065, China;
2. Siemens Signaling Company Ltd. Xi’an, Shaanxi 710016, China)
O22
A
1673-2065(2011)01-0014-03
2010-08-15
程红萍(1971-),女,陕西大荔人,西安欧亚学院数学教研室讲师,理学硕士;
赵银锋(1974-),男,陕西大荔人,西门子信号有限公司工程师.

