基于组合区域形状特征的物体检测算法
王 晏 孙 怡
①(大连理工大学信息与通信工程学院 大连 116024)
②(公安海警学院基础部 宁波 315801)
1 引言
基于特征的目标检测是计算机视觉领域中一个重要的研究方向。其基本方法主要包括两类:第1类方法是对整幅图像进行特征变换,在特征图像中搜索符合待检目标特征的片断,通过片断之间的联系确定待检目标的位置等信息。典型的算法如Vittorio等人[1,2]提出的基于局部轮廓特征的目标检测算法。在后续的研究中,作者用支持向量机分类的方法代替了特征匹配方法[3],用主动形变模型替代了手绘模型[4]。孙显等人[5]也作了相关的研究。此类方法虽然取得了较好的检测效果,但其算法结构相对复杂,对分割的要求较高。第2类方法是用多尺度窗遍历图像,判断窗内是否含有待检测目标或目标的一部分[6]。典型的算法如 Felzenszwalb等人[7]提出的一种基于多尺度、可变形物体部件模型的目标检测算法。作者后续针对固定尺度模型提出了可变尺度混合模型[8],又提出层级结构解决了速度问题[9]。类似的方法还有如张正等人[10]提出的基于部件的自动目标检测方法。但这类算法还是存在一些需要改进的方面:(1)不能给出目标的具体轮廓;(2)目标结构相对固定,针对不同复杂图案的目标存在一定的局限;(3)并非所有其他基于窗遍历的方法都能解决速度瓶颈问题。鉴于以上分析,本文实现了一种基于组合区域形状特征的目标检测算法,降低了对分割的要求,可得到目标的准确轮廓信息,不要求目标内部结构相对固定;同时,通过训练并联支持向量机分类器和对目标特征循环移位检测,保证了目标特征的旋转不变性。
2 组合区域形状特征提取
2.1 候选目标选取
采用矩形框遍历的方法不能标示出目标轮廓信息,耗时较长;而直接将图像分割的方法对图像分割要求较高。因此,本文实现了一种根据图像分割区域之间的关系提取候选目标的方法。将待检测图像分割成不同的单连通域,则待检目标一定是其中某些单连通域的组合。因此,本文在可能的单连通域组合中提取候选目标,过程如图1所示,图1(a)为原始图像,图1(b)为待检目标,图1(c)为图1(a)的分割结果,图1(d)为分割后的单连通区域,图1(e)为所有单连通区域可能的组合图像,图1(f)为本文所提取的候选目标。
首先,将图像分割成不同的单连通域。采用本文之前完成的自适应 Mean shift 算法[11]将图像分割。传统Mean shift 算法用于图像分割时没有讨论采样点权重的影响,常采用固定带宽,即使运用自适应带宽,也是完全从数据优化方面考虑的,没有考虑人眼的主观视觉特性。本文之前完成的自适应Mean shift 算法根据图像的颜色分布信息自适应选取了空域带宽。在此基础上,将评价图像质量的客观标准即频域结构相似度,与图像方差结合起来,建立了选择值域带宽的目标函数,从而使所选择带宽对应的分割图像更符合人眼的视觉特性,使分割的区域不会太细或太粗,正确表达了待检测目标的整体性。分割算法详见文献[11],分割结果如图1(c)所示,将分割后的每个单连通区域记为ri(i=1,2,…,n),如图1(d)所示,n表示所分割的单连通域总数,n=1 4。
其次,在n个单连通域中,任意选取p个形成一个新图像,记为Ik(k=1,2,…,n um),例如,r2,r8和r14可以组合成新图像I1,组合后的新图像如图1(e)所示,p取值为1,2,3,…,n-1,num表示所有新图像总数目,即
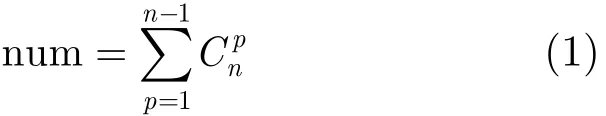
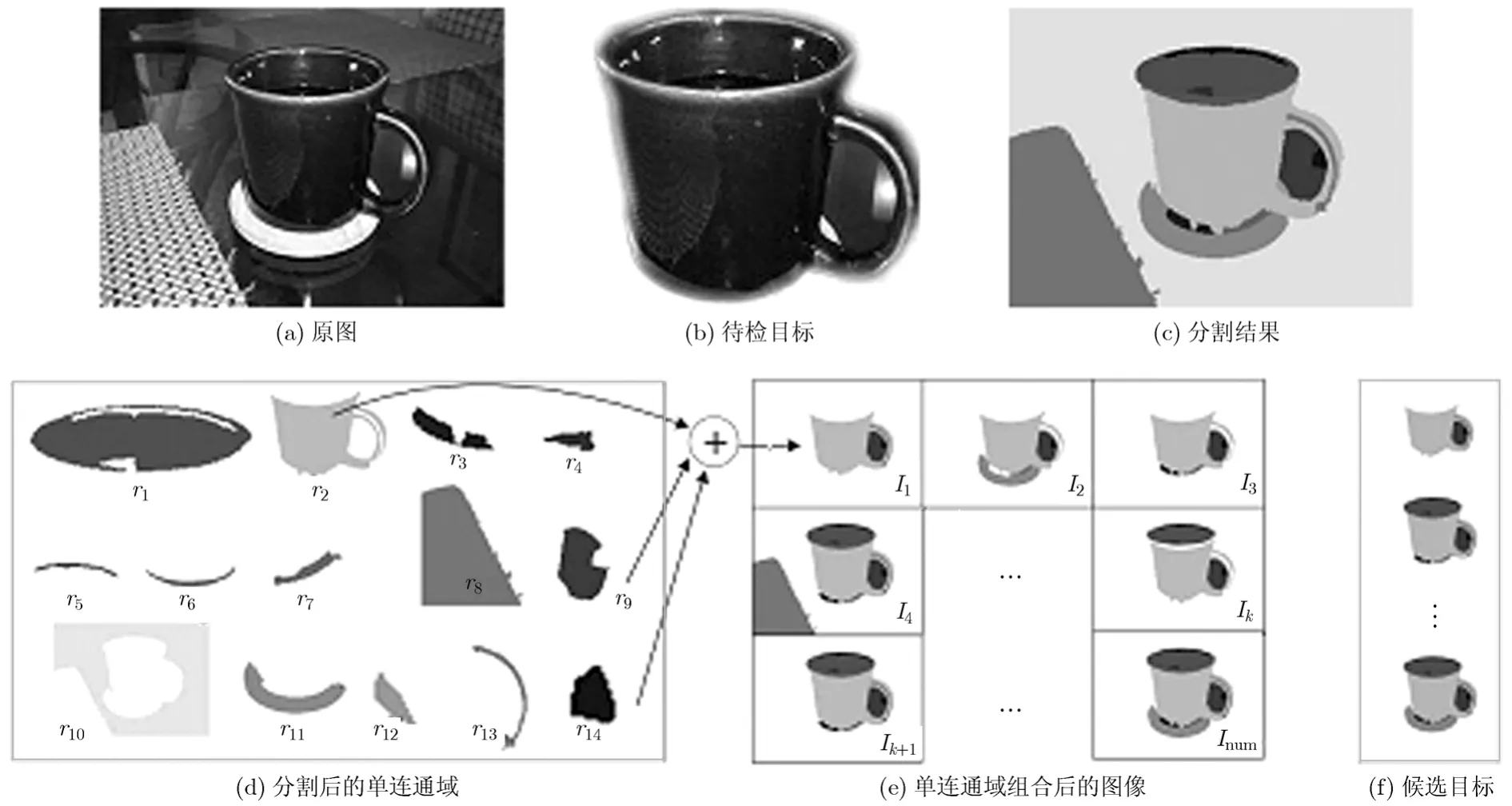
图1 候选目标示意图
表示从n个单连通域中任选p个进行组合的数目。在新图像中,有些含有多个连通域,如图1(e)中的I4,有些含有空洞,如图1(e)中的I2。本文特征提取中,只需要目标的外边界信息,因此,只将新图像中连通域个数为1并且不含空洞的图像作为候选目标,结果如图1(f)所示。可以看出,总会存在一种组合图像与待检目标相吻合。进而可以通过后续的特征提取,运用支持向量机分类器对候选目标进行检测。上述候选目标选取方法降低了分割要求,最终得到的不是表示目标位置和大小的矩形框信息,而是目标本身。
2.2 目标形状特征提取
常用特征中,颜色特征[12,13]和纹理特征[14]容易受到目标表面颜色或纹理以及光线的影响。图像变换特征[15,16],容易受到目标表面图案或形变的影响。因此,对于一般的目标检测,形状特征的适应性相对更好。形状特征分为全局特征和局部特征,全局特征如几何不变矩,对图像的局部变化比较敏感[17]。局部形状特征[18-20]都是基于边界采样点定义的,采用的是点匹配方法。在采用基于学习的分类方法时,存在待检目标特征向量的维数及元素顺序与样本特征向量不一致的问题,从而不能保证目标特征的旋转不变性。
为此,本节目的是寻找一种相对简单的形状特征,既能有效表达目标,又便于分类器的学习。如图2(a)所示,在目标的边界曲线上,以dot点为起点,将目标边界按顺时针方向分成等弧长m段,将每段弧顺序标记为sj(j=1,2,…,m),sj对应的弦记为lj,lj为有向线段,走向为顺时针方向。定义θj为从线段lj到lj+1按顺时针方向的夹角。如果以第1段弧s1为起始弧,则相邻线段之间的夹角序列为θ=[θ1,θ2,…,θm],将此序列称为夹角链码[21],它能准确地描述目标的整体形状特征,并且不容易受到局部噪声的干扰。但每一段弧对应的形状特征并没有表达在夹角链码中,因此,本文定义了弧sj到弦lj的距离最大值与弦长的比值,即弧弦距比作为目标的另一个特征,即

其中dj表示弧sj到弦lj的最大距离。如果以第 1段弧s1为起始弧,由rj构成的序列为r=(r1,r2,…,rm),它可以有效表达弧sj的弯曲程度。将θ和r共同构成的向量作为目标特征向量,记为v,即v=(θ,r)。
在上述特征提取过程中,如果起点不同,对应分段就不同,则相邻两段夹角不同。在起点相同的情况下,如果选择的起始弧不同,则特征向量中元素顺序不同,不同起始弧对应的特征向量之间存在一个相移。因此,要保证目标特征的旋转不变性,则要求待检目标与样本起点与起始弧一致,但在实际检测中很难做到这一点。因此,本文通过构造并联支持向量机实现待检目标与样本起点一致,通过对特征向量进行循环移位来克服起始弧不一致所导致的相移问题。
3 支持向量机分类器
如上所述,要保证目标特征的旋转不变性,则要求待检目标与样本的分段一致,并且计算特征向量时对应起始弧一致。
首先分析分段一致性问题,如图2(a)所示,如果以dot为起点,则分段后的段点依次为 d ot1,dot2,…,d otj-1,…,d otm-1,由于采用等弧长分段,因此,起点分别为 d ot1,dot2,…,d otj-1,…,d otm-1时对应的分段情况与以dot为起点时的分段情况是一致的。同理,在第1段弧s1上等弧长地取N个点 d ot1,dot2,…,d otN,如图2(b)所示,以这N个点中任意点为起点的分段情况和以其他段相应位置点为起点的分段情况是一致的。因此,本文在提取样本特征时,只取弧s1上的N+1个点,即 d ot,dot1,dot2,…,d otN作为分段所有情况。然后分别计算上述N+ 1 个起点分段对应的样本特征向量,记为vt0,vt1,…,vtN,分别训练不同的支持向量机分类器SVM0,SVM1,…,S VMN,如图3所示。其中,假设每个支持向量机对应的样本总数为a,则vt0,vt1,…,vtN分别是一个a行的矩阵,每一行对应一个样本特征向量。这种并联的支持向量机分类器结构可以保证,以待检目标边界上任意一点为起点对应的分段情况与训练样本的分段情况都是一致的。但是,即使在分段一致的情况下,如果计算特征向量时所选取的起始弧不同,则特征向量元素的顺序就不同,不同起始弧对应的特征向量之间存在相移。例如,在以图2(a)中的dot为起点分段的情况下,如果起始弧为s1,则对应的链码夹角向量为[θ1,θ2,…,θm],如果以s2为起始弧,对应的链码夹角向量为[θ2,θ3,…,θm,θ1]。为此,在提取候选目标特征后,将其特征向量进行m-1次循环移位,如图3所示的vd0,vd1,…,vdm-1,其中,vd1是将vd0进行一次循环移位的结果,同理,vdm-1是将vd0进行m-1次循环移位的结果,移位过程如式(3)所示,其中,θ和r的含义同本文2.2节中所述相同。
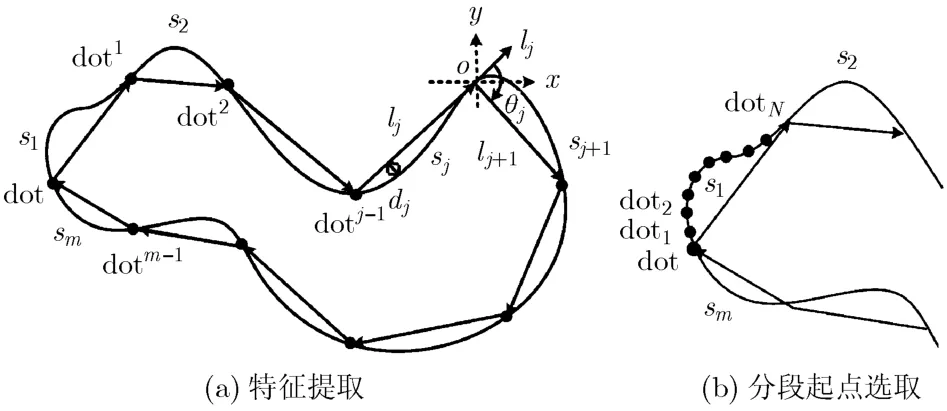
图2 特征提取示意图

图3 支持向量机分类器
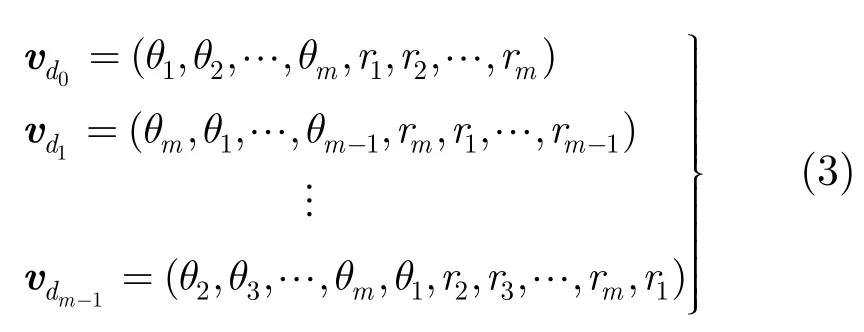
通过选取不同起点对应的样本特征向量vt0,vt1,…,vtN分别训练多个支持向量机分类器SVM0,S VM1,…,S VMN,以及对候选目标特征向量进行循环移位检测,保证了目标特征的旋转不变性。
4 实验结果分析
算法采用Matlab语言编写,实验环境为酷睿2 CPU(2 GHz),2 G内存。训练样本为实际拍摄图像,运用本文2.1节中的方法将单连通域组合成新图像,人工从中挑选出目标图像作为正样本,其他图像作为负样本。检测图像一部分来源于 ETHZ图像类库[1],另一部分来源于实际拍摄图像。实验中,将样本和候选目标大小均归一化为150×150像素,为了保证目标不变,将目标外接矩形的长边归一化为150像素,短边按照与长边相同的比例进行缩放,其他像素位置补 0。根据归一化后目标的大小,将分段参数设置为m=2 0,N=1 0是比较合理的。
(1)本文特征与Hu矩对比 为了说明本文所选特征的有效性,将其与经典的Hu矩[22]进行了对比。因为是两种特征之间的对比,不适于用传统类间距与类内间距对比,因此,将提取的夹角链码和7个Hu矩用2维曲线画在图中。图4是同一类目标的夹角链码特征与Hu矩特征,图4(a),4(b)为2幅不同角度的塑料管和鸭子图像,图4(c1),图4(d1)是其夹角链码特征,图4(c2),图4(d2)是其Hu矩特征,实线和虚线分别表示不同角度的图像特征。可以看出夹角链码特征和 Hu矩特征都能较有效地表达同一类目标。图5是不同类目标的夹角链码特征和Hu矩特征,其中图5(a),5(b)分别为塑料管、面包、鸭子和杯子的原始图像,图5(c1),图5(d1)是夹角链码特征,图5(c2),图5(d2)是Hu矩特征。实线和虚线分别表示不同的目标。从图5中可以看出,对于不同类的目标,Hu矩特征的区分能力不如夹角链码好。
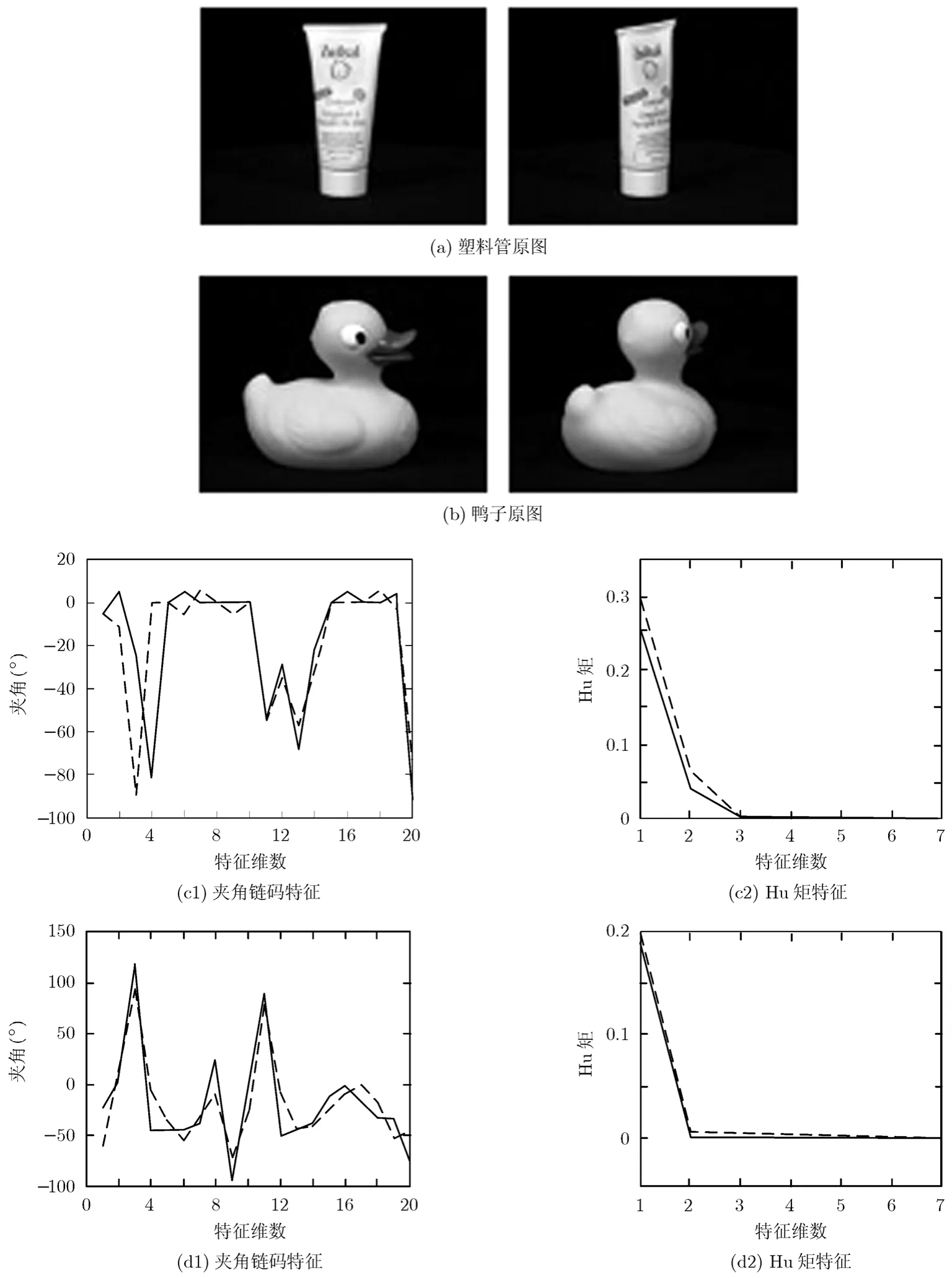
图4 同类目标特征对比
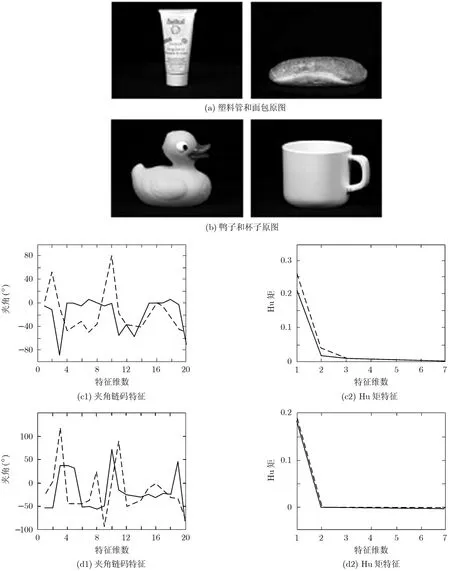
图5 不同类目标特征对比
此外,本文分别采用 Hu矩特征和链码夹角特征进行了样本检测。Hu矩特征的检测率是87%,而本文特征的检测率是94%。从检测率方面相比,本文的特征也优于Hu矩特征。
(2)分割结果对检测的影响分析 本文采用3组参数下的Mean shift分割算法[11]对目标为杯子的图像进行分割和检测,图6(a),6(b),6(c)分别为3组不同参数下的检测结果,杯子以白色轮廓标示。参数r,w分别为Mean shift算法的空域带宽和值域带宽,本文设置r=8,分别取w=0 .29Wx,w=0.13Wx,w=0 .05Wx,Wx为采样点与被平滑点差的平均值。
针对3组不同参数,分割单连通域个数不同,但本文方法降低了分割要求,只要目标外边界轮廓分割没有严重失真,通过单连通域组合,总有一个组合情况与杯子相对应,因此,即使目标内部分割错误,也不影响最终检测结果,只在杯子边缘部分稍有不同。
此外,表1列出了不同参数对应的单连通域个数、选取候选目标所用的时间和候选目标数,并与基于可变尺度矩形框选取候选目标的方法所用的时间和所确定的候选目标数做了比较。其中,实验图像大小为261×349像素,遍历矩形框初始大小为50 × 50像素,终止大小为200 × 200像素,遍历步长为2像素。可以看出随着值域带宽w减小,分割区域数增加,选取候选目标的时间增多,候选目标数增大。但是,确定候选目标的时间基本不会超过1 s,并不会很大程度上增加检测时间。而矩形框遍历的方法所用的时间和确定的候选目标数远大于本文方法。

图6 不同分割结果下的检测结果

表1 不同方法及分割结果对应的候选目标情况
为了验证本文算法的适应性,分别对杯子图像进行了模糊和调节对比度操作,对其中比较模糊、严重模糊、对比度较低和对比度很低4种情况的图像进行了检测,结果用白色轮廓标示在图7中,结果表明本文对严重模糊和对比度很低的图像都能正确检测。实际上,针对不同图像,很难给出一个确定的阈值用来衡量不能检测目标时所对应的模糊程度和对比度。
(3)目标检测结果及分析 本文对 ETHZ图像类库中48幅杯子图像、48幅酒瓶图像和40幅苹果标志图像作了检测实验,结果以白色轮廓标示在图8(a)中,结果表明本文算法可以正确检测待检目标。此外,在错误目标率为0.3的情况下,在表2中统计了杯子图像的检测率。其中,错误目标率表示非目标被检为目标的数目与非目标数目之比,检测率是指检测出的目标数目与目标总数之比。除本文检测率之外,其他数据来自文献[3]。
(a)计算效率:文献[3]中,不考虑图像预处理情况,检测一幅图像的时间只需要1 s。本文算法在和文献[3]采用近似相同条件下,不考虑图像分割和选取候选目标的过程,检测较为简单和较为复杂的图像所用时间范围为 0.33~2.7 s,部分图像的检测时间比文献[3]长,但文献[3]是在工作站实现的,硬件环境要好于本文的实验环境。
(b)计算复杂度:文献[3]建立kAS积分直方图的复杂度为将kAS与码书对应的复杂度为其中,W×H为图像大小,r为直方图的空间分辨率,N为kAS的个数,为码书的大小,k为所取的相邻段的个数。本文候选目标提取的复杂度为O((A+ 1)×n+A),特征提取的复杂度为O(gns+gnT),其中,n为分割的区域数,A为区域的最大像素数,gn为候选目标数,g为比例系数,s为目标边界的分段数,本文取s=20,T为边界分段后每段的像素数的最大值。可以看出,本文的算法复杂度和文献[3]的算法复杂度同阶。
(c)表2中本文检测率略低于 PAS算法检测率的主要原因,其一是由于分割造成的误判和漏检,其二是由于支持向量机分类器产生的误判和漏检。
本文算法复杂度与文献[3]同阶,计算时间与文献[3]相当,检测率接近文献[3]的检测率,但与其相比,本文算法避免了多尺度矩形窗遍历图像的方法,对分割要求不高,算法流程结构比较简单,更易于实现。
本文算法对ETHZ图像类库之外背景相对比较复杂或者目标本身结构比较复杂的图像也可以正确检测,如图8(b)所示。但是,对于目标本身颜色与背景颜色近似的图像,会出现漏检,如最后一幅杯子图像。
总之,造成误判和漏检的原因有两个方面:(1)支持向量机分类器产生的误判和漏检;(2)由分割造成的误判和漏检。

图7 模糊和低对比度图像的检测结果

图8 目标检测结果

表2 检测率表
5 结论
本文针对基于可变尺度矩形框遍历的候选目标选取方法中存在的问题,实现了一种在分割基础上组合选取候选目标的方法,此方法既能降低对分割的要求,同时也能在模糊和低对比度图像中提取出候选目标,可以得到目标的轮廓信息,而不是表示位置和大小的矩形框信息,并且计算时间远小于基于矩形框遍历的方法。在此基础上,提取了目标的夹角链码特征和弧弦距比特征,构造了并联支持向量机分类器,从而真正保证了目标特征的旋转不变性。
[1]Vittorio F,Tinne T,and Van Gool L.Object detection by contour segment networks[C].Proceeding of 9th European Conference on Computer Vision.Graz,Austria,2006:14-28.
[2]Vittorio F,Frederic J,and Cordelia S.Accurate object detection with deformable shape models learnt from images[C].Proceeding of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Minneapolis,USA,2007:564-571.
[3]Vittorio F,Loic F,Frédéric J,et al..Groups of adjacent contour segments for object detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2008,30(1):36-51.
[4]Vittorio F,Frederic J,and Cordelia S.From images to shape models for object detection[J].International Journal of Computer Vision,2010,87(3):284-303.
[5]孙显,王宏琦,杨志峰.基于形状统计模型的多类目标自动识别方法[J].电子与信息学报,2009,33(11):2626-2631.Sun Xian,Wang Hong-qi,and Yang Zhi-feng.Automatic multi-categorical objects recognition using shape statistical models[J].Journal of Electronics&Information Technology,2009,33(11):2626-2631.
[6]Mohan A,Papageorgiou C,and Poggio T.Example-based object detection in images by components[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(4):349-361.
[7]Felzenszwalb P F,McAllester D,and Ramanan D.A discriminatively trained,multiscale,deformable part model[C].IEEE Conference on Computer Vision and Pattern Recognition,Anchorage,Alaska,USA,2008:1-8.
[8]Felzenszwalb P F,Girshick R B,McAllester D,et al..Object detection with discriminatively trained part-based models[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(9):1627-1645.
[9]Felzenszwalb P F,Girshick R B,and McAllester D.Cascade object detection with deformable part models[C].IEEE Conference on Computer Vision and Pattern Recognition,San Francisco,USA,2010:2241-2248.
[10]张正,王宏琦,孙显,等.基于部件的自动目标检测方法研究[J].电子与信息学报,2010,32(5):1017-1022.Zhang Zheng,Wang Hong-qi,Sun Xian,et al..An automatic method for targets detection using a component-based model[J].Journal of Electronics&Information Technology,2010,32(5):1017-1022.
[11]王晏,孙怡.自适应mean shift算法的彩色图像平滑与分割算法[J].自动化学报,2010,36(12):1637-1644.Wang Yan and Sun Yi.Adaptive mean shift based image smoothing and segmentation[J].Acta Automatica Sinica,2010,36(12):1637-1644.
[12]Chen Xi-lin,Yang Jie,Zhang Jing,et al..Automatic detection and recognition of signs from natural scenes[J].IEEE Transactions on Image Processing,2004,13(1):87-99.
[13]Chang Shyang-lih,Chen Li-shien,Chung Yun-chung,et al..Automatic license plate recognition[J].IEEE Transactions on Intelligent Transportation Systems,2004,5(1):42-53.
[14]Kim Kwang-in,Jung Keechul,Park Se-hyun,et al..Support vector machines for texture classification[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(11):1542-1550.
[15]Begum N,Alam M,and Islam M I.Application of canny filter and DWT in fingerprint detection[C].13th International Conference on Computer and Information Technology,Cape Town,South Africa,2010:256-260.
[16]Li He-xi,Wang Guo-rong,Shi Yong-hua,et al..The automatic recognition of welding targets based on normalized svd of image matrix[C].Proceeding of the 2007 IEEE International Conference on Mechatronics and Automation,Harbin,China,2007:3100-3104.
[17]Xu Chun-jing,Liu Jian-zhuang,and Tang Xiao-ou.2D shape matching by contour flexibility[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(1):180-186.
[18]Chetverikov D.A simple and efficient algorithm for detection of high curvature points in planar curves[C].Proceeding of 10th International Conference on Computer Analysis of Images and Patterns,Groningen,The Netherlands,2003,(2756):746-753.
[19]Belongie S,Malik J,and Puzicha J.Shape matching and object recognition using shape contexts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(4):509-522.
[20]Grigorescu C and Petkov N.Distance sets for shape filters and shape recognition[J].IEEE Transactions on Image Processing,2003,12(10):1274-1286.
[21]赵宇,陈艳秋.曲线描述的一种方法:夹角链码[J].软件学报,2004,15(2):300-307.Zhao Yu and Chen Yan-qiu.Included angle chain:a method for curve representation[J].Journal of Software,2004,15(2):300-307.
[22]Hu Ming-kuei.Visual pattern recognition by moment invariants[J].IRE Transactions on Information Theory,1962,8(2):179-187.

