广域监视模式下新的杂波加噪声谱密度矩阵估计方法
闫 贺 郑明洁 李 飞 艾加秋②
①(中国科学院电子学研究所 北京 100190)
②(中国科学院研究生院 北京 100039)
1 引言
对宽广的区域存在的动目标进行检测、定位、跟踪在民用和军用领域均有迫切的需求,在民用领域,可以实现重点区域的交通流量控制;在军用领域,可以提供战区的部队调动情况,为战场指挥官提供重要的决策信息。
广域监视模式是一种通过天线的电扫描或机械扫描来实现对大范围的、感兴趣的区域中存在的运动目标进行全天时、全天候监视的工作模式。这种工作模式相对于条带 SAR/GMTI模式有自己的特点:可以多次从多个角度照射到运动目标,提高运动目标的检测概率,使得对目标运动轨迹的描述成为可能[1]。美国的 AN/APY_3(JSTARS),AN/APY-8(Lynx),TeSAR,HiSAR,ARL-M,德国的PAMIR,英国的ASTOR,以色列的EL/M-2055,北约的 SOSTAR-X等雷达系统都具有广域监视的工作模式,这些雷达系统对地面动目标进行检测时面临的最大问题都是如何抑制较强的地杂波。现在已经知道美国的JSTARS系统采用的是杂波抑制干涉方法(CSI)[2]而德国的 PAMIR系统采用的是Scan-MTI算法[3-5]。CSI算法是一种通道对消的算法,而 Scan-MTI算法是一种空时处理算法,两种算法在处理实际数据中均取得了较好的结果。
本文对广域监视模式进行了研究,安排如下:在第2节,证明了广域监视模式下,当满足一定的条件时,每个多普勒单元的杂波谱密度矩阵的秩均为1;第3节在第2节的基础上,推导了一种新的杂波加噪声谱密度矩阵估计方法,并分析提出:通过第i-1和第i+1个多普勒单元的信息来估计第i个多普勒单元的杂波加噪声谱密度矩阵结合特征矢量子空间投影的方法可以大大减弱目标污染样本的影响;第4节仿真了两种波束指向下场景的回波,并采用上述方法和常规谱密度矩阵求逆方法对场景回波进行处理,显示了本文所提方法在处理目标污染样本时的优越性;在第5节中得出结论。
2 广域监视模式下杂波特性分析
Ender[6,7]指出在SAR-GMTI模式下,采用1DT算法时[8],如果方位向PRF满足Nyquist采样定律,则每个多普勒单元对应的杂波谱密度矩阵的秩为1(文献[9-11]进一步讨论了该算法在SAR-GMTI模式中的应用),但该结论的前提是方位向时间带宽积必须比较大。在广域监视模式下,波束在每个扫描波位上停留的时间非常短,方位向时间带宽积不可能满足该条件,因此不能就此认为广域监视模式下每个多普勒单元的杂波谱密度矩阵的秩也为 1。下面对广域监视模式下每个多普勒单元的杂波谱密度矩阵的秩进行研究,并且假设方位向PRF满足Nyquist采样定律。
与SAR成像模式下的回波类似,广域监视模式下的每个通道的回波仍然可以看成系统的冲激函数和随时间变化的地面后向散射系数之间的卷积,即
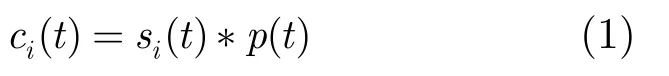
ci(t)表示第i个通道(相对于参考通道)的回波。通过空间几何关系(如图1所示)可知第i个通道经过距离压缩后的冲激函数可以表示为
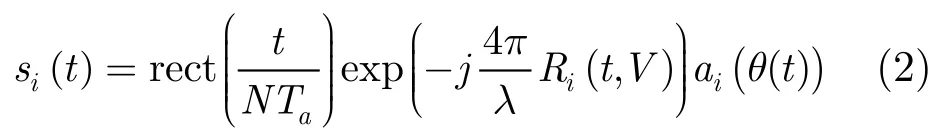
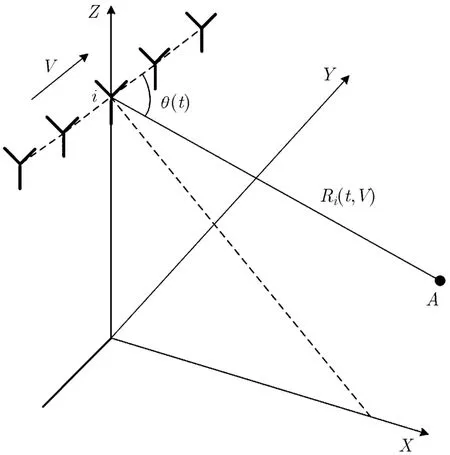
图1 广域扫描时的几何关系图
式(2)中的Ta表示方位向发射脉冲重复时间,N表示在一个扫描波位上发射的脉冲数。由空间几何关系可知,地面静止点和载机的实时距离可以近似表示为

式中V表示载机飞行的速度,Ri0表示地面静止点和载机的初始距离,Ri(t,V)表示地面静止点和载机的实时距离。从式(2)可以看到,系统的冲激函数由 3部分组成,其中第3部分是由天线的双程加权和通道的位置差异(相对参考通道)而导致回波在幅度和相位上的变化,由天线的知识可知

式(4)中,Di(θ(t))表示天线的双程加权,ri表示第i个通道相对参考通道的距离差。通常广域监视系统在设计的时候,一个扫描波位的驻留时间是非常短的,ai(θ(t))的变化很小,可以认为是不变的,这里改用ai(θ)表示。
对式(2)进行傅里叶变换可得
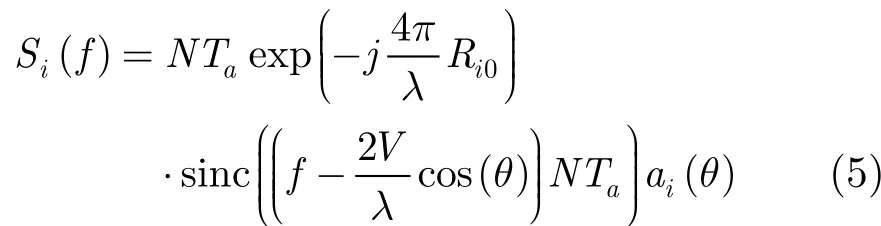
根据方位向多普勒频率和方位角度的一一对应关系,ai(θ)可以写成
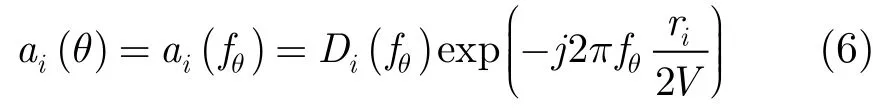
其中fθ表示θ对应的多普勒频率。将式(6)代入式(5),并将结果写成向量的形式(这是对所有通道的联合表达式),可知
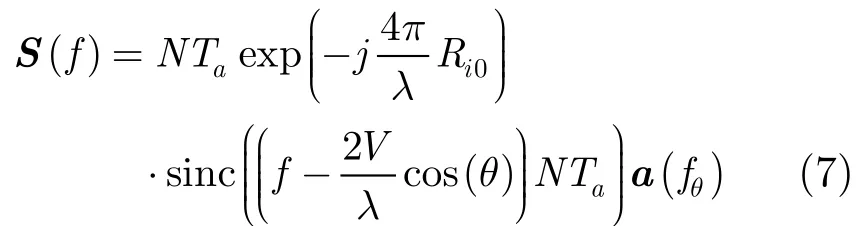
在进行方位向FFT的处理中,根据每个波位上的方位向采样点数N对系统PRF进行分割,这样相邻两个频率采样点的间隔为PRF/N,根据方位向多普勒频率和方位角度的一一对应关系可知这实际上是将场景在方位向上进行分割,可以把方位向分割的每个块产生的回波等效成位于该块中心的点产生的回波,这种等效处理在方位向采样点越多的情况下越精确[12]。利用这种等效处理,可得方位向FFT变换后第k个多普勒单元对应的表达式应该为
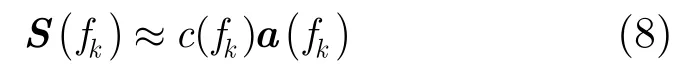
其中c(fk)表示与多普勒频率fk有关的复常数。需要说明的是为了简化公式推导,上述考虑的是不加权的方位向FFT变换,实际采用1DT算法处理时使用的是方位向加权FFT变换,这样处理可以大大抑制来自其他多普勒单元的杂波,减轻空域滤波负担,但同时会导致该多普勒单元杂波谱展宽。
根据Ender在文献[13]中的结论(假设杂波在空间上的分布是平稳的),第k个多普勒单元对应的杂波谱密度矩阵为
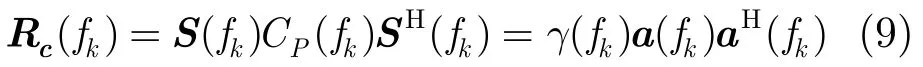
其中CP(fk)表示杂波的功率谱,γ(fk)表示与多普勒频率fk有关的复常数。通过式(9)可知第k个多普勒单元对应的杂波谱密度矩阵秩为1,如果让k遍历所有的多普勒单元,可得到结论:在广域扫描时,如果方位向PRF满足Nyquist采样定律且每个扫描波位上的脉冲数足够多,则任意多普勒单元对应的杂波谱密度矩阵的秩均为 1。根据此特点,我们可以采用特征矢量子空间投影方法来计算滤波器的权系数[4]。
如果把噪声分量(设噪声功率为σ2,且噪声是白噪声)也考虑进去的话,并认为杂波和噪声之间是不相关的,可以得到第k个多普勒单元的杂波加噪声谱密度矩阵。
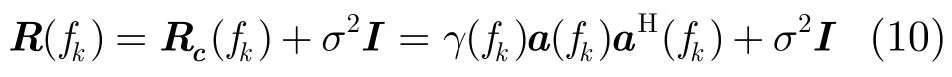
其中σ2表示噪声经过距离压缩和方位 FFT处理后的功率。
3 新的杂波加噪声谱密度矩阵估计方法
根据第2节中的结论可以得到一种新的谱密度矩阵估计方法:通过某个多普勒单元的杂波加噪声谱密度矩阵来估计另一个多普勒单元的杂波加噪声谱密度矩阵,下面给出推导过程。
假设通过最大似然估计方法从回波数据(RD域)中得到第k个多普勒单元的杂波加噪声谱密度矩阵为
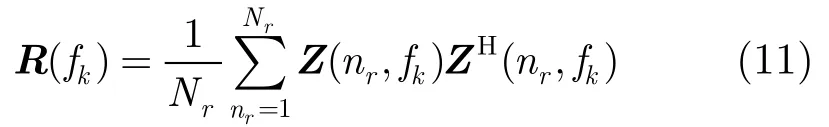
其中Nr为待处理的距离单元数,Z(nr,fk)表示第r个距离单元第k个多普勒单元的回波矢量。
如果想通过第k个多普勒单元的杂波加噪声谱密度矩阵来估计第j个多普勒单元的杂波加噪声谱密度矩阵,根据第2节中的推导可知R(fk)和R(fj)可写成如下形式:
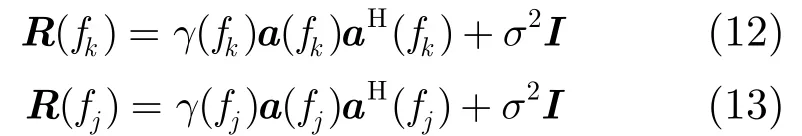
则需要在第k个多普勒单元的杂波加噪声谱密度矩阵上补偿相应的幅度和相位因子。由文献[13]可知,如果存在这样的转换矩阵
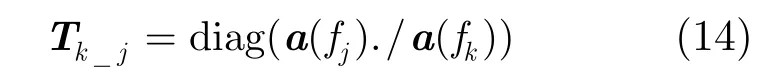
其中“./”表示向量或矩阵的点除运算。也就是说它满足

那么我们可以得到(因为γ(fk)≈γ(fj))
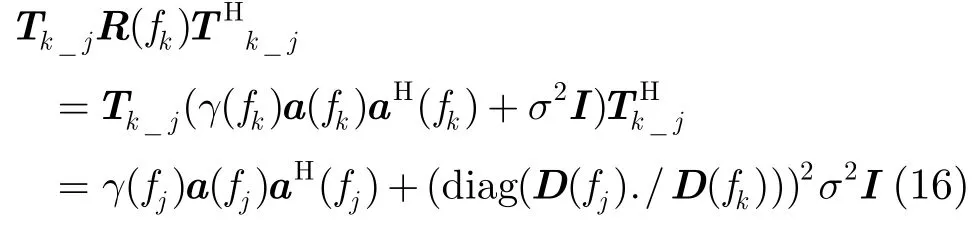
则通过第k个多普勒单元估计的第j个多普勒单元的杂波加噪声谱密度矩阵为
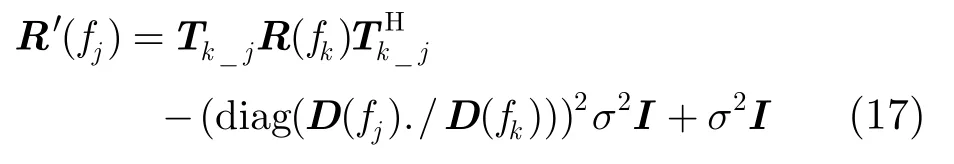
也就是说对通过最大似然方法估计的第k个多普勒单元的杂波加噪声谱密度矩阵乘上相应的转换矩阵,再对噪声功率分量进行适当的调整,就可以近似得到第j个多普勒单元的杂波加噪声谱密度矩阵。整个信号处理流程如图2所示。
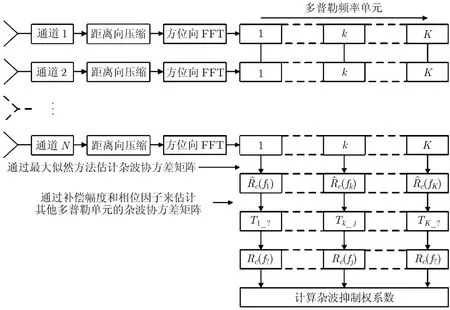
图2 新的杂波加噪声谱密度矩阵估计方法流程图
另外,在上述处理过程中,需要知道天线方向图的频率域表达式,它是从回波数据中估计得到的[1]。
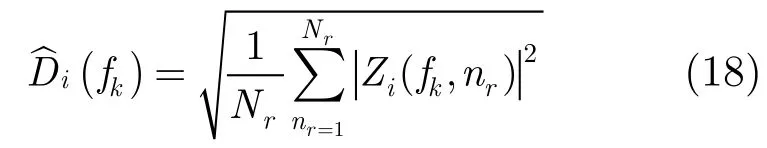
(fk)表示的是第i个通道第k个多普勒单元对应的天线方向图的频域表达式的值。
对于 SAR/GMTI系统广域监视模式,由于距离分辨率比一般的预警雷达高的多,在进行空时处理时,会有充足的距离单元样本来估计杂波加噪声谱密度矩阵。但如果对每个距离单元都单独进行杂波加噪声谱密度矩阵的估计会使运算量急剧增加,所以通常对广域扫描数据作如下的简化处理:选取一段距离单元,并用该段内所有的距离单元作为样本来估计一个杂波加噪声谱密度矩阵,然后将它用于该段内全部距离单元的杂波抑制[3-6]。文献[12]指出如果含有目标导向矢量的信号混入到训练样本中相对于功率的非均匀性对自适应滤波器性能的影响更大。据此本文提出新的杂波加噪声谱密度矩阵估计算法:通过第i-1个和第i+1多普勒单元的信息来估计第i个多普勒单元的杂波加噪声谱密度矩阵,结合式(11)-式(17),可知其处理过程如下:
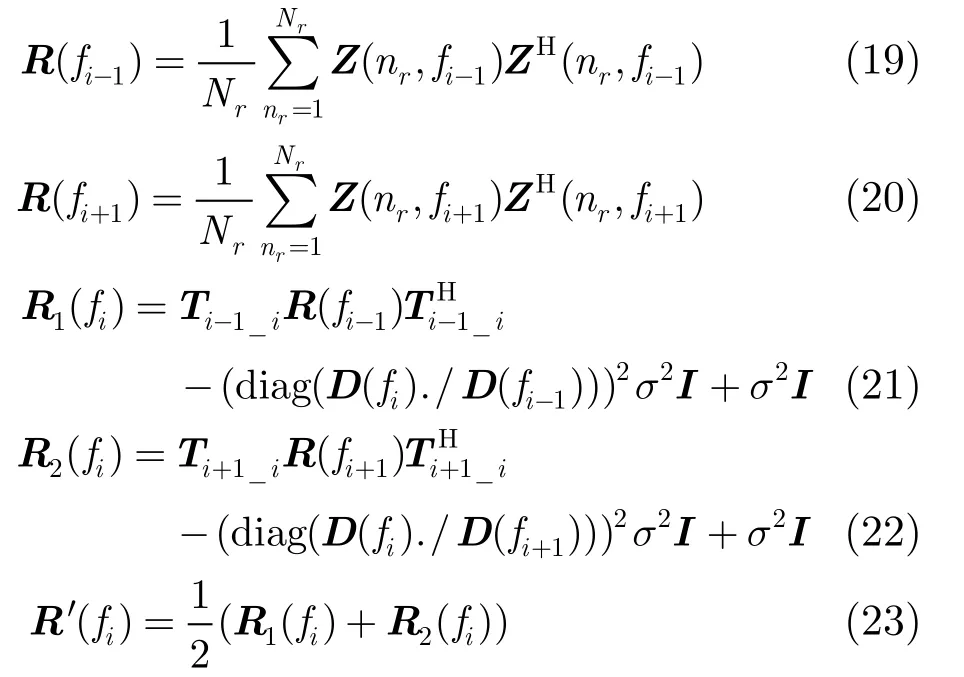
其中转换矩阵为
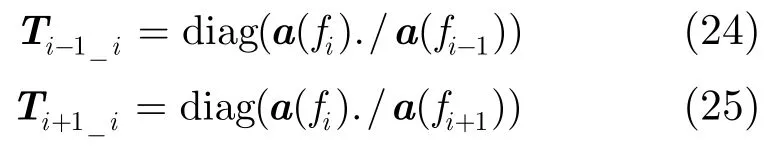
需要说明的是,我们并没有采用奇异检测算法剔除被目标污染的样本[14],而是直接用所有待测的距离单元作为样本,通过大量的样本的平均作用来减弱目标污染样本的影响,接着通过第i-1个和第i+ 1 个多普勒单元的信息来估计第i个多普勒单元的杂波加噪声谱密度矩阵,这样处理的好处是:如果用第i个多普勒单元的数据来估计自身的杂波加噪声谱密度矩阵,则存在于第i个多普勒单元的运动目标会导致自适应滤波输出的杂波剩余增加而目标信号减弱,引起虚警率提高而目标检测性能下降,但通过第i-1个和第i+1个多普勒单元的信息来估计第i个多普勒单元的杂波加噪声谱密度矩阵可以大大减弱存在第i个多普勒单元的运动目标的影响,同时这相当于把用来估计杂波加噪声谱密度矩阵的样本数增加了一倍。
在此基础上,根据第2节的结论,在方位向PRF满足Nyqiust采样定律的时候,可以通过特征矢量子空间投影的方法来设计第i个多普勒单元的杂波抑制滤波器矩阵[4]。
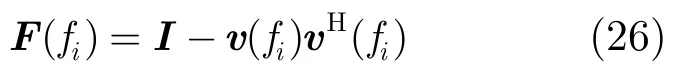
其中v(fi)表示R′(fi)最大特征值对应的特征向量。从理论上讲,该滤波器可以将杂波抑制到噪声水平。
则用于该段所有距离单元的第i个多普勒单元的滤波器可以表示为
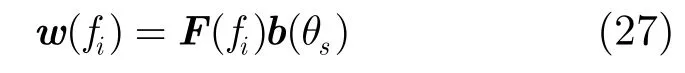
其中b(θs)表示天线指向对应的波束形成器。
4 算法仿真及分析
为了验证上述杂波加噪声谱密度矩阵估计方法的有效性,本文在计算机上进行了仿真实验,系统的仿真参数和PAMIR系统基本类似,见表1所示。这里选取了波束指向为0°(正侧视)和15°两种情况下场景的回波(假设地面后向散射系数服从高斯分布),在每个距离单元上按照一个多普勒单元对应一个方向角,在每个方位角上布置1个点目标,所以在每个距离单元上都布置了128个点,并截取了第1000-1299距离单元共300个距离单元的回波数据。

表1 仿真系统参数
在两种情况下的场景回波中都加入了幅值相同的6个动目标信息,且都位于波束指向的中心,经过距离压缩和方位向 FFT后的SNR≈20 dB,CNR≈30 dB,他们的速度和所处距离单元见表2。

表2 回波中加入的动目标信息
为了表述方便,这里把通过第i-1个和第i+1个多普勒单元的信息估计第i个多普勒单元的杂波加噪声谱密度矩阵并联合特征矢量子空间投影的方法,称为算法1,把直接通过第i个多普勒单元的所有距离单元来估计自身的杂波加噪声谱密度矩阵并对该矩阵直接求逆的方法,称为算法 2,将波束指向0°时的场景,称为场景1,将波束指向15°时的场景,称为场景2,在处理仿真回波时采用的是1DT处理算法。
把5个通道接收到的回波数据进行距离压缩和方位向FFT变换到RD域,图3(a),图3(b)分别表示了通道3接收到的场景1,场景2的RD域回波功率图,从图中可以看出6个动目标均被杂波所淹没。
图4(a)、图4(b)分别表示场景1和场景2的回波经过算法1进行杂波抑制后的功率图,从两幅图中可以看出杂波得到了有效的抑制,6个动目标信息均凸显出来,从而表明了算法1的有效性。
为了显示算法 1在处理目标污染样本时的优势,这里将算法1和算法2的处理结果进行了对比,如图5,图6所示。分别选取波束指向0°时第1个目标的距离向切面图和波束指向15°时第5个目标的距离向切面图,并考察了样本数目依次选取 300,100,50时的情况。从图5(a),图5(b)中可以看出,采用算法2进行杂波抑制后,目标的相对功率(相对噪声功率)随着样本数目的减少而降低,在图5(a)中,目标1的相对功率分别为:18.5 dB(300),14.5 dB(100),12.5 dB(50),在图5(b)中,目标5的相对功率分别为:18.8 dB(300),16.2 dB(100),12.9 dB(50)。这是因为当样本数目比较多时,含有运动目标信息的样本的影响会因较多样本数目的平均作用而被大大削弱,但是这种影响会随着样本数目的减少而逐渐显现出来。而从图6(a),图6(b)中可以看出,采用算法1进行杂波抑制后,目标的相对功率几乎不随样本数目的减少而变化,在图6(a)中,目标1的相对功率均为20 dB,在图6(b)中,目标5的相对功率均为19 dB,可见算法1有效地避免了目标污染样本的影响。
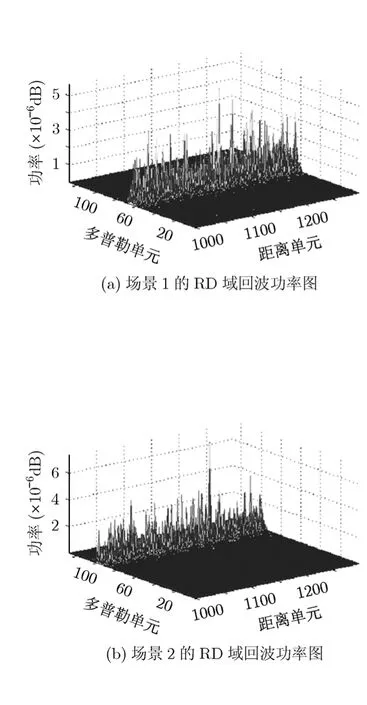
图3 通道3接收到两个场景的回波功率图
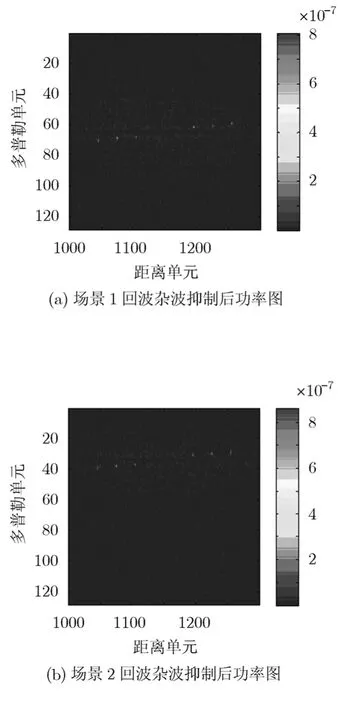
图4 采用算法1处理后回波功率图
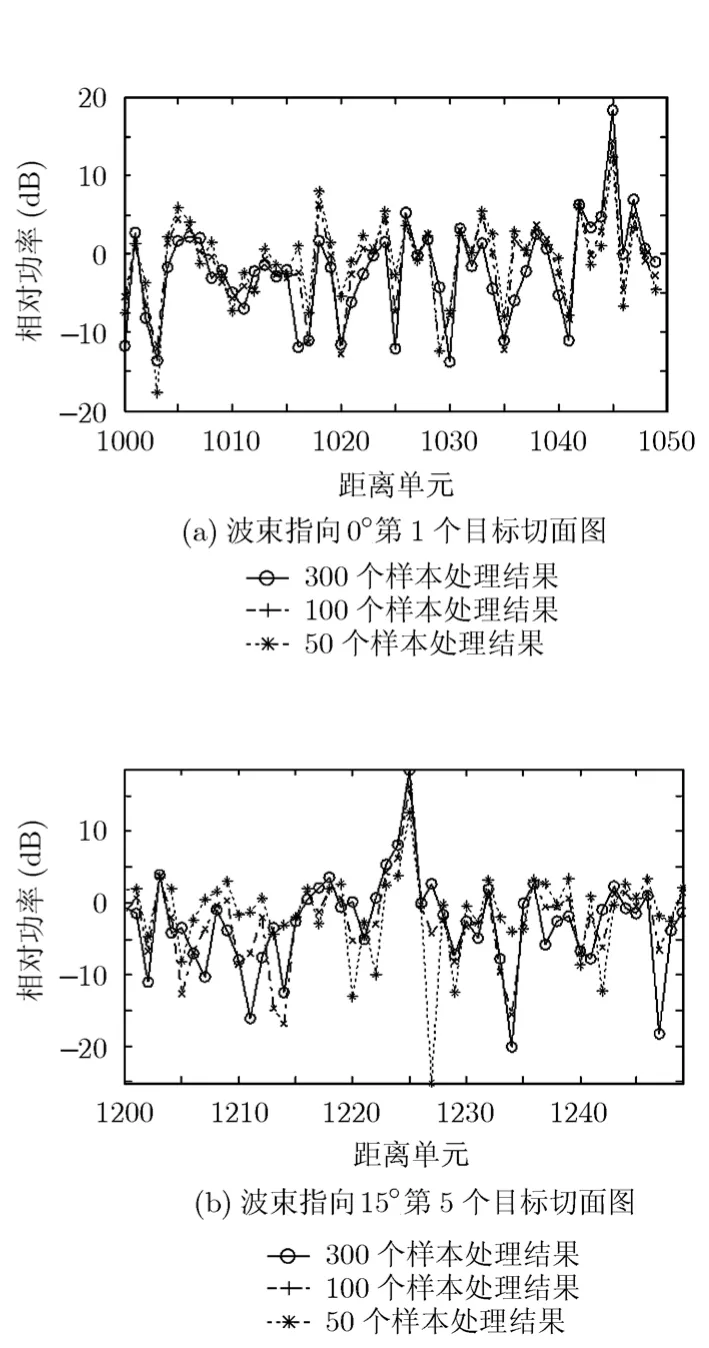
图5 算法2处理时不同样本情况下目标切面图
5 结论
本文首先证明了广域监视模式下进行杂波抑制时,如果方位向采样点数足够多,在方位向PRF满足Nyqiust采样定律时,每个多普勒单元的杂波谱密度矩阵的秩为1,然后推导了通过第k个多普勒单元的杂波加噪声谱密度矩阵来估计第j个多普勒单元的杂波加噪声谱密度矩阵的计算公式,在此基础上提出通过第i-1个和第i+1个多普勒单元的信息来估计第i个多普勒单元的杂波加噪声谱密度矩阵的方法,联合特征矢量子空间投影可以大大减弱目标污染样本对空时处理性能的影响,最后结合PAMIR系统的参数,验证了上述方法的有效性。
图6 算法1处理时不同样本情况下目标切面图
[1]Cerutti-Maori D,Klare J,Brenner A R,et al..Wide-area traffic monitoring with the SAR/GMIT system PAMIR[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(10):3019-3030.
[2]Entzminger J N,Senior J R,Fowler C A,et al..JointSTARS and GMTI:past,present and future[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(2):748-761.
[3]Cerutti-Maori D,Gierull C H,and Ender J H G.Experimental verification of SAR-GMTI improvement through antenna switching[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(4):2066-2075.
[4]Wilden H and Brenner A R.The SAR/GMTI airborne radar PAMIR:technology and performance[C].IEEE MTT-S,Anaheim,California,May 23-28,2010:534-537.
[5]Ender J H G,Berens P,Brenner A R,et al..Multi channel SAR/MTI system development at FGAN:from AER to PAMIR[C].European Conference on Synthetic Aperture Radar,Toronto,2002:1697-1701.
[6]Ender J H G.Space-time processing for multichannel synthetic aperture radar[J].Electronics&Communication Engineering Journal,1999,11(1):29-38.
[7]Ender J H G.Detection and estimation of moving target signals by multi-channel SAR[C].European Conference on Synthetic Aperture Radar,Königswinter,Germany,1996:411-417.
[8]Ward J.Space-time Adaptive Processing for Airborne Radar[M].NASA STI/Recon Technical Report N,1994:109-119.
[9]魏俊,孙进平,袁运能,等.一种基于频域 STAP处理的多通道 SAR-GMTI算法[J].系统工程与电子技术,2008,30(1):1-5.Wei Jun,Sun Jin-ping,Yuan Yun-neng,et al..New multi-channel SAR-GMTI frequency STAP algorithm[J].Systems Engineering and Electronics,2008,30(1):1-5.
[10]齐维孔,禹卫东.多载频星载MIMO-SAR系统动目标检测技术研究[J].电子与信息学报,2010,32(10):2365-2370.Qi Wei-kong and Yu Wei-dong.Research on ground moving target indication for spaceborne MIMO-SAR of multiple carrier-frequencies[J].Journal of Electronics&Information Technology,2010,32(10):2365-2370.
[11]张晓光,刘祥峰,付琨.基于 MIMO-SAR体制的空频域自适应动目标检测技术研究[J].电子与信息学报,2010,32(8):1997-2001.Zhang Xiao-guang,Liu Xiang-feng,and Fu Kun.Study on ground moving target indication of multiple input multiple output space-borne SAR[J].Journal of Electronics&Information Technology,2010,32(8):1997-2001.
[12]吴迪,朱岱寅,朱兆达.基于改进 FRACTA 算法的多通道SAR 动目标检测技术[J].电子与信息学报,2010,32(9):2201-2207.Wu Di,Zhu Dai-yin,and Zhu Zhao-da.Moving target detection for multi-channel SAR based on improved FRACTA algorithm[J].Journal of Electronics&Information Technology,2010,32(9):2201-2207.
[13]Ender J H G.Subspace transformation techniques applied to multi-channel SAR/MTI[C].IEEE International Geoscience and Remote Sensing Symposium,Hamburg,Germany,July 1999:38-40.
[14]吴建新.机载相控阵雷达STAP及目标参数估计方法研究[D].[博士论文],西安电子科技大学,2009.

