超高斯加载的稳健自适应波束形成及性能分析
邹 翔 钟子发 张 旻
(电子工程学院 合肥 230037)
(安徽省电子制约技术重点实验室 合肥 230037)
1 引言
波束形成是阵列信号处理中广泛应用的一项关键技术,如雷达、声纳、MIMO无线通信、医疗成像、麦克风语音处理等领域。传统的自适应波束形成方法假定期望信号(Signal Of Interest,SOI)的导向矢量是精确已知的,然而,实际应用中导向矢量失配误差会引起波束形成性能急剧下降,近年来涌现了几种稳健的波束形成方法来解决这种失配问题[1-5]。Li等人[1,2]对导向矢量的不确定集进行建模,通过对角加载(Diagonal Loading,DL)的方法,相当于对输出矢量增添了2-范数惩罚项,获得与该不确定集参数有关的稳健自适应算法。Vorobyov等人[3,4]分别提出了基于最坏情况性能最优(Worst Case)和基于概率约束的方法,其中最坏情况性能最优最终也可以转化为对角加载方法[3,6]。由于对角加载方法具有简单有效的优点,许多研究者对其进行了深入的研究[7-10]。
标准对角加载方法在加载电平合适时能有效地提高导向矢量不确定时波束形成器的稳健性,其对应的先验分布是高斯的,范数p=2。然而,由于实际应用中不确定性误差不仅来自于导向矢量,还来自于采样方差矩阵估计,而后者和快拍数、信噪比、干噪比、干扰个数以及信号与干扰的来波方位都有关系,这种不确定性非常难以建模,从而造成波束形成器整体性能的下降。为了实现导向矢量误差和样本方差矩阵误差的总体最优修正,通过对稳健波束形成的优化问题进行分析,本文提出了一种基于p范数的对角加载方法,p∈(1,2),用来对整个不确定性进行综合考虑,我们称之为超高斯加载的稳健自适应波束形成(Super-Gaussian Loading,SGL),文中采用遗传算法(Genetic Algorithm,GA)得到最优的p值。SGL方法把复杂的模型估计问题利用非整范数转化为相对描述简单的超高斯加载问题,避免了建模带来的估计误差,文中对p范数优化问题给出了基于凸优化的解决方案。实验结果显示,当使用范数p∈(1,2)时,SGL都比DL方法有更高的输出信干噪比;而使用最优的p时,可以获得最优的性能提高,稳健性更强。
2 超高斯加载的自适应波束形成
假设M阵元均匀线阵,接收L个窄带信号,则在时刻t阵列接收到的信号为
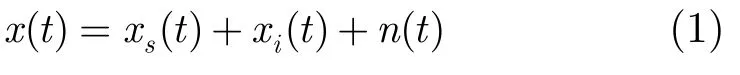
其中xs(t),xi(t),n(t)分别是统计独立的期望信号、干扰和噪声。这里xs(t)=,s0(t)是期望信号波形,a0=a(θ0)是期望信号的实际导向矢量。
自适应波束形成器的输出

其中w=[w1,…,wM]T∈CM是波束形成权值复向量,(⋅)T和(⋅)H分别代表矩阵的转置和共轭转置。
样本数据的自相关矩阵为
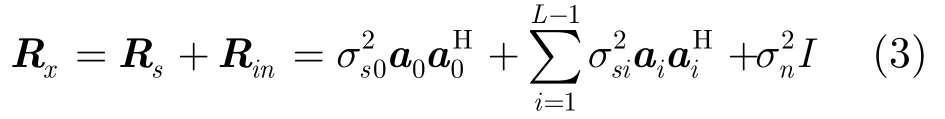
这里,分别是期望信号和第i个干扰的功率。
基于输出功率最小准则,则自适应波束形成可以写成以下优化问题:
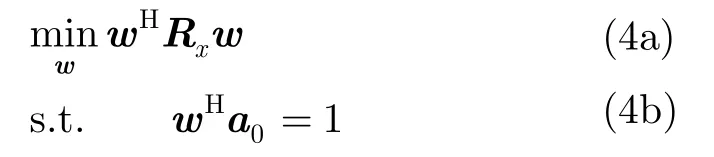
最优解是
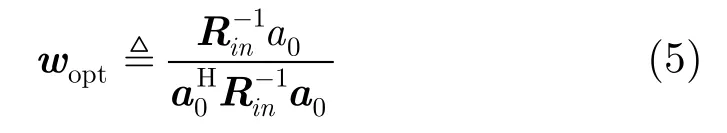
这里Rin是干扰加噪声协方差矩阵,由于在实际处理中无法得到Rin,通常用Rx的估计值来代替,即在时间上多次快拍采样对X(i)XH(i)求平均来完成,N为快拍数,令Rx的估计值为
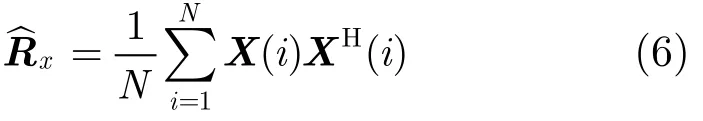
样本矩阵直接求逆方法(Sample Matrix Inversion,SMI)给出的解为
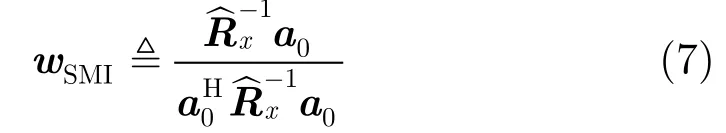
在很多情况下,无法精确得到期望信号的方向,或者期望信号的DOA在一定方位内缓慢移动,这种情况下,来波估计会存在一定的估计误差,从而导致波束形成器性能的下降。这就需要稳健的自适应波束形成算法来提高其鲁棒性,尤其当Δθ=|-θ0|处于的较小邻域内,是期望信号DOA的估计值。对角加载方法是解决此类问题的有效手段之一,其优化问题描述和解分别为
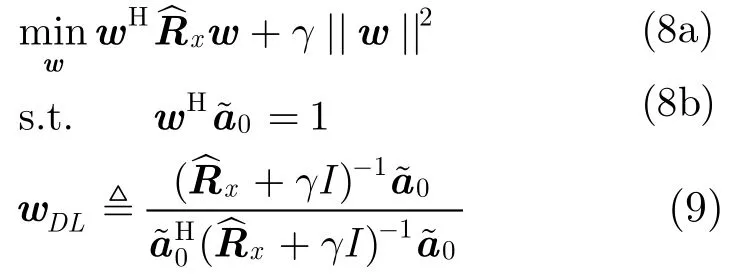
比较式(4)和式(8)就可以看出,对角加载方法不但使用代替a0,还使用代替Rx,所以对样本方差矩阵的估计误差不能够忽略。观察式(8)发现,如果使用ℓ2范数“惩罚”w,来修正导向矢量的不确定性(对应线性相乘wH,见式(4)),那么就会“过于惩罚”的不确定性(对应二次方相乘wH),由此可见使用2-范数可能不是最优的。考虑到整个波束形成器的不确定性,我们将其转化为p-范数惩罚将更为合理。

其中p-范数表示为
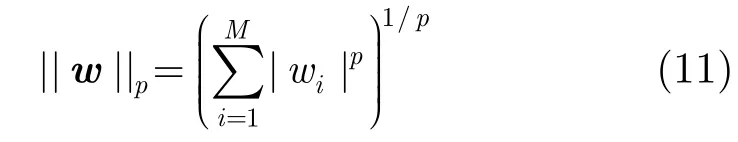
这里wi是w的第i个元素,γp是加载电平。
2.1 广义高斯分布
广义高斯分布的概率密度函数f(w)如下所示:
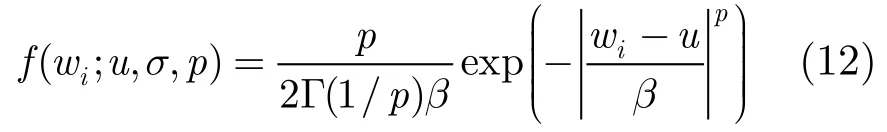
其中

这里Γ(⋅)代表Gamma函数,Γ(z)=。参数u,σ,β,p分别称为广义高斯分布的均值,标准方差,尺度参数和形状参数,尺度参数β是方差控制参数。本文情况μ=0,γp=1/βp。当p=2时,就是标准对角加载特例,其先验分布就是高斯分布。当1≤p<2,其先验分布就是超高斯的。当p变化时,γp也会跟着变化从而使得前后方差一致。例如,如果标准对角加载的加载电平为γ2,那么当使用ℓp范数时其加载电平则变化为
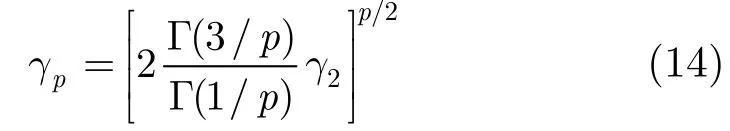
2.2 算法求解
尽管式(10)不能够通过推导来求得w的显式解,但是我们可以借鉴最差性能最优算法[3]利用凸优化来求解。根据凸优化理论,任何p>1的范数都是凸函数,所以式(10a)目标函数是关于w的凸函数。所以此优化问题可以转化成二阶锥规划的形式[11],使用内点法可以高效地求解权值w[12,13]。
2.3 最优p的确定
任意给定p,由利用2.2节方法从式(10)可以得到w,即w是p的一个函数。输出信干噪比(Signal to Noise-plus-Interference,SINR)是衡量数字波束形成算法的最重要指标之一。于是定义p为
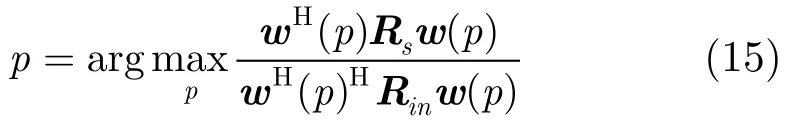
然而,实际上为我们只能得到,无法得到,它们是未知的。但通过特征分解,得到
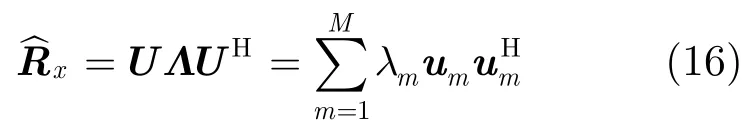
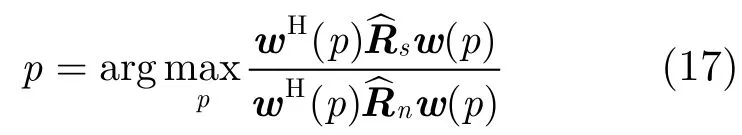
可以看出,变成了信号和干扰的方差矩阵的近似,而仅代表噪声自相关矩阵的近似。由于输出权值用来零陷干扰,w(p)在干扰子空间上的投影是很小的,所以这种置换是合理的。
遗传算法是一种基于自然遗传演化机制的高效搜索算法,由遗传算法理论得知,当选定初始种群以后,把式(17)作为适应度函数,经过若干代的进化淘汰,最后的种群应该是最优的p值群。本文设计实验采用遗传算法求取最优p的精确解。仿真实验中假设阵列为半波长均匀线阵,所加噪声为零均值的高斯白噪声,假设期望信号的方向角为0°,3个干扰,其中实验结果来自100次独立的蒙特卡洛实验。
具体求解p遗传算法包括以下5个步骤:
(1)初始化种群。选取P{p|1.000<p≤5.000},即在(1.0,5.0]区间随机产生40个个体,每个p精确到小数点三位。
(2)编码。用一个整数排列表示。设任意

其中sj∈{0,1}。由于12位可以表示0~212-1之间的数,例如1.500=(010111011100)2/1000这样,每个个体都被表示成一个12位整数列的形式。
(3)适应度评价。令
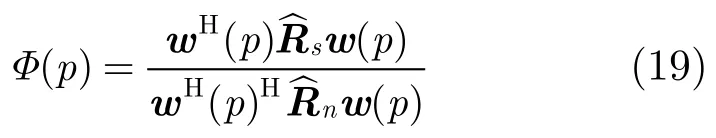
作为适应度函数,φ值越大,适应度越高。
(4)遗传操作。个体的遗传操作主要包括交叉、变异和选择。交叉采用随机单点交叉的方式,交叉概率pc取0.6<pc<0.8。变异方式为单点变异,变异概率pm取0.001<pm<0.01。对个体选择采用常用的轮盘赌的方法,由于选择、交叉、变异等操作的随机性,可能会破坏当前群体中最好的个体,所以采用最优保留策略确保最好的个体始终遗传到下一代。
最后一代输出的分布示意图如图1所示,其算术平均值为1.255。
2.4 范数p的泛化性
上节中获得的最优p是在固定参数情况下得到的,在实际情况下,参数如、信噪比(SNR)和干噪比(INR)是变化的(实际应用中阵元数基本不变),从而导致最优的p有一定的波动范围,但是通过分析式(10)得知,,都是因为变化而变化。
于是我们定义导向矢量失配误差

则ε是角度的函数,也就是说,ε是影响最优p的主要因素。如果在不同的误差情况下遗传算法给出的最优p≈1.255都有很好的性能,则说明p=1.255具有很好的泛化性,是比较理想的选择。
当固定阵元数M=10,SNR=INR=10dB时,输出信干噪比在不同误差ε情况下与p的关系如图2所示。可以发现,随着角度误差的增大,SINR的峰值在减小,但是无论误差大小如何,最大的SINR总出现在p≈1.255处。另外,通过变化信噪比和干噪比,也发现p在1.255附近一直有着最好的性能,说明p=1.255具有很强的稳健性,验证了遗传算法求解的正确性。由此可以判定,当使用对角加载方法时,最优的惩罚项不应该是2-范数的,而应该是p-范数的,p≈1.255。当使用这一范数时,总会获得比2-范数更好的输出信干噪比。
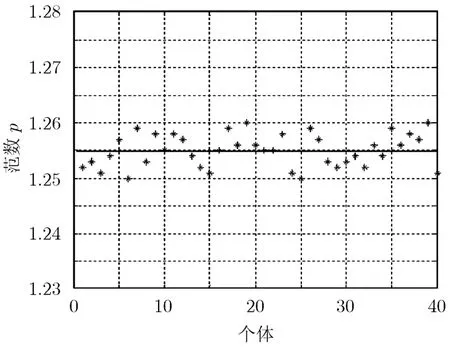
图1 最后种群的p值分布图
3 仿真实验
为了验证算法的有效性,仿真实验比较了SGL和DL算法在不同加载电平,不同快拍数、不同信噪比和不同导向矢量误差下的性能。假设阵列为半波长均匀线阵,所加噪声为零均值的高斯白噪声。假设3个干扰分别从30°,70°和-30°入射,期望信号的方向角为0°,实验结果来自100次独立的蒙特卡洛实验。
实验1实验1仿真SGL和DL两种方法在不同加载电平下的输出信干噪比SINR。此时固定SGL范数p=1.255,快拍数K=200,阵元数M=10,SNR=-5dB,INR=30dB,图3分别给出了不同观测误差下的性能比较图,可以看出尽管输出SINR随着加载电平的增大有一定的波动,但在所有的加载电平下SGL比DL有更好的输出信干噪比,高出3dB左右。
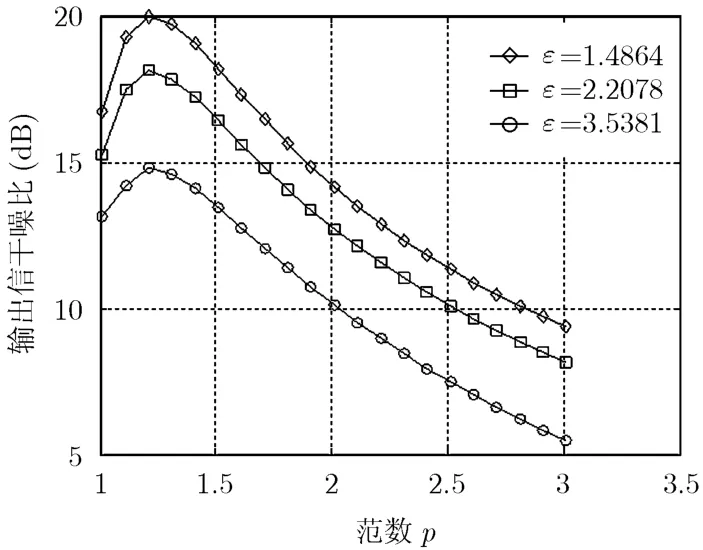
图2 输出SINR与范数p的关系曲线
实验2下面两个实验固定DL算法中的加载电平为10,相应地,SGL中的加载电平根据式(14)得到,这出于几种原因:一是目前还没有根据和观测角度就能确定加载电平的标准方法;二是从实验1可以知道,加载电平在较大的范围内波动却可以产生近似的SINR。为简便起见,本实验固定SNR=0 dB,其余条件同实验1。仿真几种算法在不同快拍数下输出信干噪比。如图4所示,从图4(a)-4(c)观测误差依次增大,可以发现,无论观测误差大小如何,在相同的快拍数条件下,SGL比DL方法的输出信干噪比高出2 dB左右。
实验3实验条件同实验1,仿真输出SINR与角度失配误差Δθ的关系。如图5,从图中可以看出,随着信号方向失配的变化,输出SINR也跟着变化,当失配的角度误差在[-3°,3°]时,SGL有较高的输出SINR。而且在仿真实验中,SGL方向图也准确指向了实际的信号方向。因此,SGL波束形成算法在信号失配情况下具有良好的稳健性。
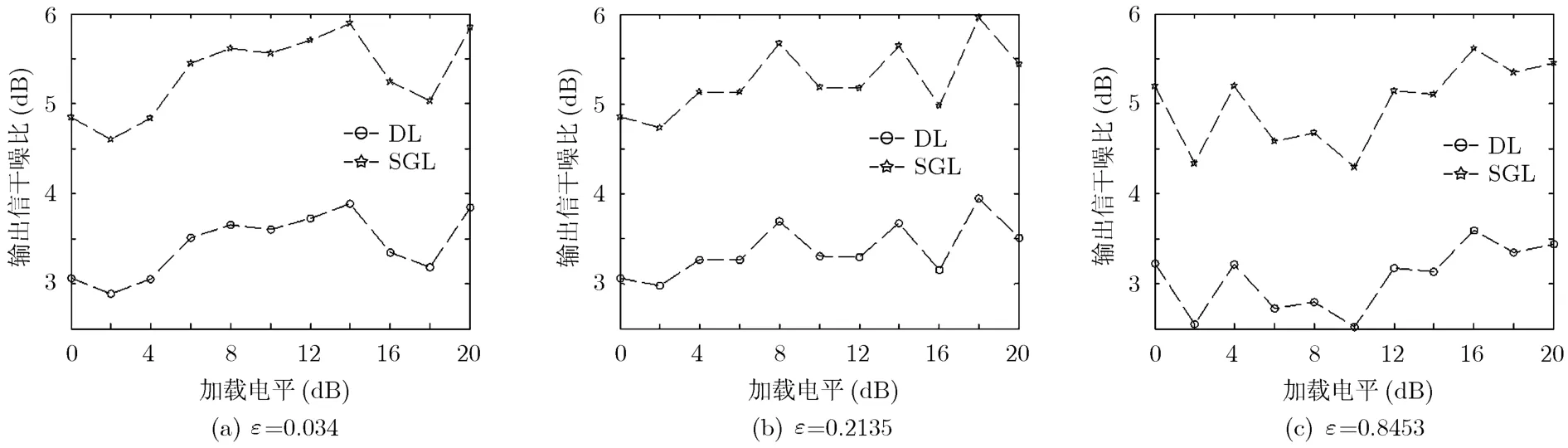
图3 输出SINR与加载电平的关系
实验4仿真几种算法在不同输入SNR情况下输出 SINR的大小,这也是衡量波束形成算法性能好坏最常用的评价方法。从图6(a)-6(c)角度观测误差Δθ依次为0.5°,1.5°,3.5°,其余实验条件同实验 1。可以发现在角度误差Δθ较小时(小于2°),SGL比Worst Case有更好或相当的性能,但是当观测误差Δθ较大时(大于3°),Worst Case在高信噪比区域比SGL方法稍好,实验3的结果也从侧面验证了这一点。几乎在任何信噪比区域,超高斯加载方法都有比对角加载方法更为优越或相当的性能,这是因为SGL利用非整范数,对导向矢量和样本方差矩阵的失配进行了综合考虑和折中,在稳健性和自适应性之间找到了平衡,从而达到总体性能的最优。

图4 输出SINR与快拍数的关系
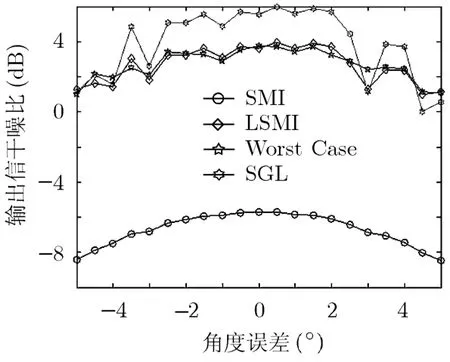
图5 输出SINR与角度估计误差Δθ的关系
4 结论
本文提出了一种超高斯加载的稳健自适应波束形成算法,其中使用的最优范数p1 .255,用来实现对角度估计误差和协方差矩阵误差的总体最优修正。文中对p范数优化问题给出了基于凸优化的解决方案,设计的一系列实验显示,提出的算法有更高的输出信干噪比,提高了稳健性和性能优势。在角度误差和加载量相同的情况下,比对角加载方法有更好的性能;在失配量较小时,稳健性也稍优于最差情况性能最优算法。
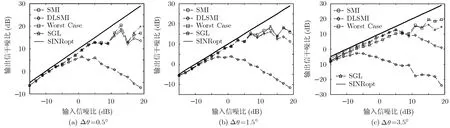
图6 几种算法的输出SINR比较
[1]Li J,Stoica P,and Wang Z.On robust capon beamforming and diagonal loading[J].IEEE Transactions on Signal Processing,2003,51(7):1702-1715.
[2]Li J,Stoica P,and Wang Z.Doubly constrained robust capon beamforming[J].IEEE Transactions on Signal Processing,2004,52(9):2407-2423.
[3]Vorobyov S A,Gershman A B,and Luo Z Q.Robust adaptive beamforming using worst-case performance optimization:a solution to the signal mismatch problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.
[4]Vorobyov S A,Chen Haihua,and Gershman A B.On the relationship between robust minimum variance beamformers with probabilistic and worst-case distortionless response constraints[J].IEEE Transactions on Signal Processing,2008,56(11):5719-5724.
[5]邹翔,张旻,钟子发.基于失配误差正交分解的稳健自适应波束形成[J].电子与信息学报,2010,32(10):2320-2323.Zou Xiang,Zhang Min,and Zhong Zi-fa.Robust adaptive beamforming based on mismatch errors orthogonal decomposition[J].Journal of Electronics&Information Technology,2010,32(10):2320-2323.
[6]刘聪锋,廖桂生.最差性能最优通用信号模型稳健波束形成算法[J].电子学报,2010,38(6):1249-1255.Liu Cong-feng and Liao Gui-sheng.Robust beamforming algorithm for general signal models using worst-case performance optimization[J].Acta Electronica Sinica,2010,38(6):1249-1255.
[7]Elnashar A,Elnoubi S M,and EI-M Ikatih A.Further study on robust adaptive beamforming with optimum diagonal loading[J].IEEE Transactions on Antennas and Propagation,2006,54(12):3647-3658.
[8]Li J,Lin D,and Stoica P.Fully automatic computation of diagonal loading levels for robust adaptive beamforming[C].ICASSP 2008,Las Vegas,Nevada,USA,March 30-April 4,2008:2325-2328.
[9]戴凌燕,王永良,李荣锋,等.基于不确定集的稳健Capon波束形成算法性能分析[J].电子与信息学报,2009,31(12):2931-2936.Dai Ling-yan,Wang Yong-liang,Li Rong-feng,et al..Performance analysis of robust capon beamforming based on uncertainty set[J].Journal of Electronics&Information Technology,2009,31(12):2931-2936.
[10]Gu Y J,Zhu W P,and Swamy M N S.Adaptive beamforming with joint robustness against covariance matrix uncertainty and signal steering vector mismatch[J].Electronics Letters,2010,46(1):86-88.
[11]鄢社锋,马远良.二阶锥规划方法对于时空域滤波器的优化设计与验证[J].中国科学E辑,信息科学,2006,36(2):153-171.
[12]Boyd S and Vandenberghe L.Convex Optimization.Cambridge University Press.Available at http://www.stanford.edu/~boyd/cvxbook.html,2004.
[13]Grant M and Boyd S.Cvx users’ guide for cvx version 1.2.http://www.stanford.edu/~boyd/cvx.html,2009.

