协作分集技术AF模式下反馈延迟随机性分析
汪三骏 黄生叶
(湖南大学信息科学与工程学院 长沙 410082)
1 引言
随着个人通信技术的发展,无线通信系统需要提供高速率的数据业务(Gbps),抗衰落技术也要求更高。多天线(MIMO)技术被认为是对抗衰落的有效方法。无线终端由于受到体积、功率、实现等因素的限制,使得多天线难以在终端实现。Sendonaris等人[1]提出的协作分集(CD)通过小区内用户的协作形成虚拟MIMO,具有提供空间分集克服多径衰落、延伸覆盖、增加系统容量等特点,是对抗无线衰落和提供空间分集的有效方法[2]。
文献[3-5]对中继放大协作分集(CD-AF)和中继解码转发协作分集(CD-DF)方式的系统性能进行了研究。中继放大协作分集是每个节点只是简单地放大和转发节点接收到的信号到目的节点,中继解码转发协作分集是每个节点解码和重新编码接收到的信号,然后转发到目的节点。CD-DF模式有助于避免错误信号扩大,而CD-AF结构简单效率高。
文献[6]基于协作分集 AF模式下,研究了源节点的排队问题和信道的自适应编码技术结合下的系统模型和平均延迟。本文在AF协作分集通信系统中结合自适应调制编码技术,以源节点发送一个数据帧到接收到目的节点的反馈信息的延迟的随机性分布为研究目标,分析了三节点协作分集网络由于发送链路以及在不同信道条件下调制编码模式不同造成的反馈延迟的随机性。引入有限状态马尔科夫信道模型分析信道的相关性,进一步研究由信道相关性造成的信道调制编码模式的相关性,最后得出反馈延迟的稳态概率分布。
2 系统模型
图1是由一个源节点S,一个目的节点D和一个中继节点R组成三节点放大中继协作通信系统(CDAF)的结构图[6],所有节点均只有一根天线,其中hd,hs,hr分别是S→D,S→R,R→D路径的衰落系数幅度,相互独立,服从Nakagami-m分布,信道噪声服从均值为0、方差为nd,ns,nr的复高斯分布。
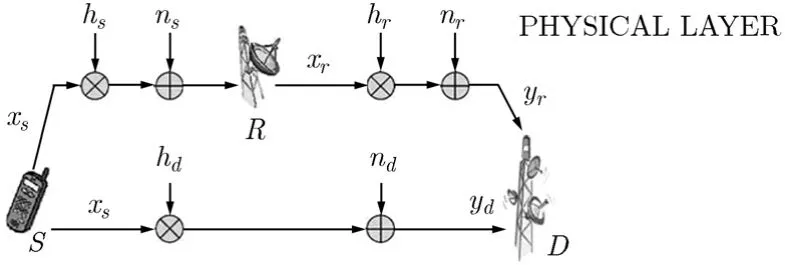
图1 CD-AF结构图
对于三节点协作分集AF模式下数据帧发送流程如下:
(1)源节点S发送数据帧以广播的形式发送,目的节点和中继节点都接收到数据帧,目的节点验证处理接收到的数据帧,如果目的节点验证数据帧正确,反馈一个ACK给源节点,发送过程结束。
(2)如果目的节点验证数据帧错误,那么就等待中继节点转发的数据帧,在接收到中继转发的数据帧之后同样对接收到的数据帧进行验证处理,如果正确,就反馈一个 ACK给源节点,如果错误,就反馈一个NACK给源节点,一次发送过程结束。
Nakagami-m分布能够比较充分地描述多径效应,Nakagami-m分布相对瑞利分布、对数正态分布、莱斯分布能更准确地与实验数据相吻合,并且具有更好的灵活性与广泛的适应性[7]。本文假设图1中3条信道的衰落系数幅度相等,信道噪声方差也相等。Nakagami分布用以下分布函数来描述接收包络大小的分布
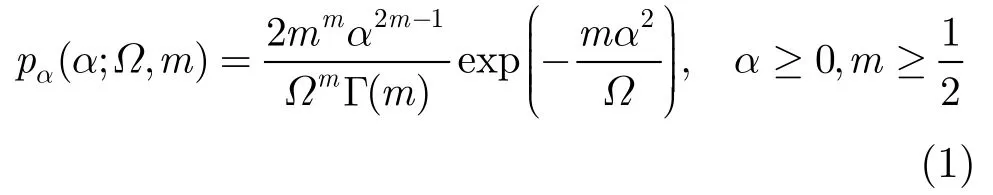
Γ(m)=是Gamma函数,瞬时的符号信噪比的概率密度函数为
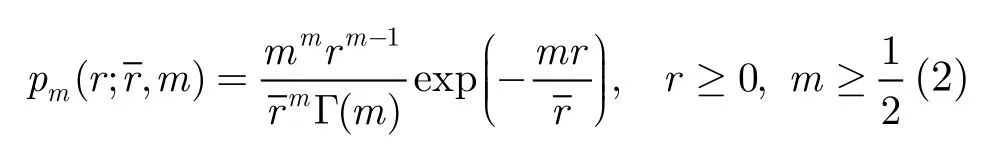
≈E{γ} 是平均接收信噪比,m(m≥ 1 /2)是Nakagami衰落参数,表示不同分集的衰落信道。假设可以采用的编码调制模式有N种,每种编码调制模式的速率为Rn(n=1,2,…,N),可将信噪比划分为N+ 1 个连续区间,区间门限为γn(n=1,2,…,N),当γn≤γ<γn+1(γ0=0;γN+1=+∞)时,选择调制编码模式n发送下一帧[8]。为了避免信道深衰落,当γ0≤γ<γ1时不发送数据时是0模式。在0模式的情况下R0=0。首先来确定信噪比的门限值,这里采用误帧率准则,根据信道编码采用卷积码时的瞬时误帧率与信噪比的关系[9]

n是调制编码模式序号,γ是接收信噪比,an,gn,γpn是在数据帧大小Ns为1080 bits时由实验拟合实际误帧率曲线的参数[10]如表1。

表1 信道编码与调制方式
在给定最大误帧率Pmax的情况下可以得到
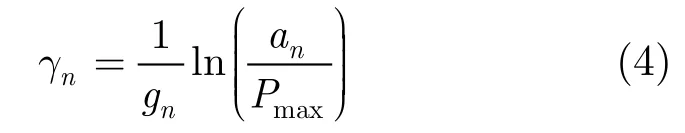
在物理层,当信噪比γ∈[γn,γn+1)时,使用编码调制模式n,瞬时信噪比落在每个区间的概率[11]为
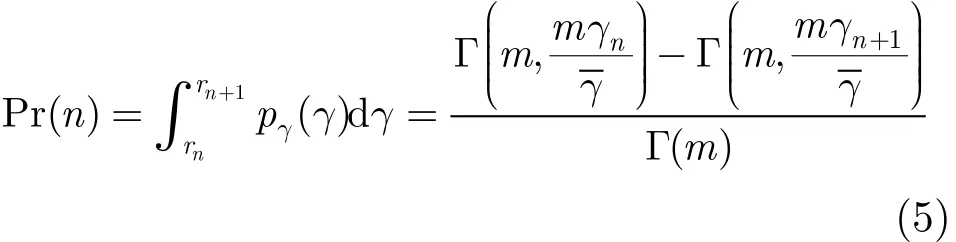
当信噪比γ∈[γn,γn+1)使用调制编码模式n时,直接链路S-D的信道平均误帧率[8]
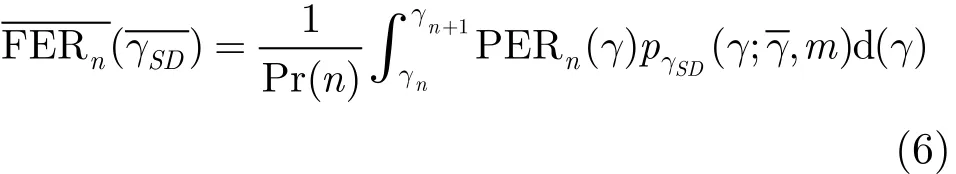
3 Markov信道模型
一般情况下,无线衰落信道是无记忆信道,但是当数据传输速率较高时,无线信道被认为是慢变的,在这种信道中传输的相邻数据帧之间的相关性就不容忽视。此时,采用传统的无记忆信道模型,引入的误差就较大,而更接近这种记忆信道的一种模型是马尔可夫信道模型,它充分利用了相邻数据帧之间的相关性来提高性能。马尔可夫信道模型输出衰落信道的基带差错序列,而不是衰落信道的包络,这样可以简化仿真过程。有限状态马尔可夫信道模型(Finite State Markov Channel,FSMC)[11,12]将接收信号的SNR量化为有限的状态,然后采用一阶有限态Markov模型实现。本文提出采用一阶FSMC模型对Nakagami-m分布衰落信道进行建模,将信道根据SNR值的大小分割为连续的几个区间,每个区间即信道的一个状态。
图2是有限状态马尔科夫信道模型,我们考虑的信道是慢衰落的情况,所以信道在相邻的时隙之间变化,信道状态超过2的转移概率为0,在文献[11-14]中有
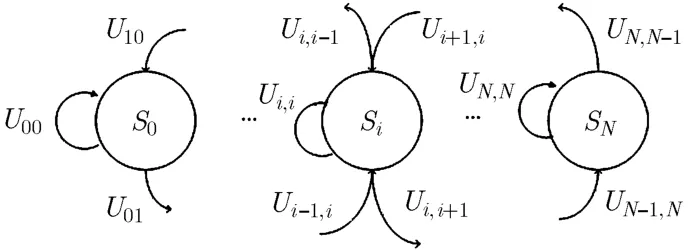
图2 有限状态马尔科夫信道模型

相邻的信道状态的转移概率可以得到[12]

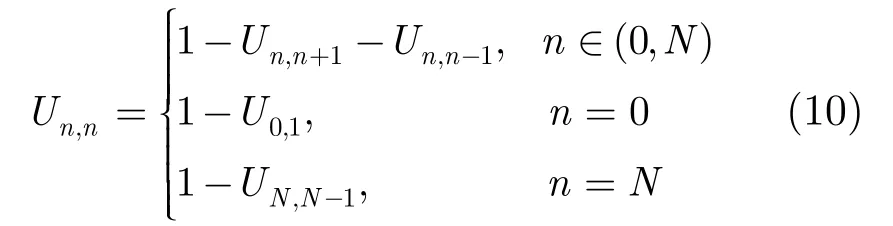
信道状态转移矩阵可表示为

4 反馈延迟分析
由第2节中系统模型AF模式下数据帧发送流程,可以得到一次数据帧发送过程的反馈延迟。当直接链路S-D数据帧传输正确时反馈延迟为

在一个时隙里信道状态不变,中继节点的调制编码模式与源节点一致,当直接链路S-D数据帧传输错误,数据帧通过中继链路S-R-D到达目的节点情况的反馈延迟为
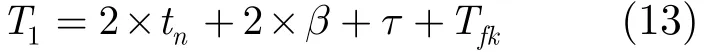
其中n代表信道编码模式,tn=Ns/Cn为传输延迟,Cn代表n模式下的传输速率,β代表传播延迟,β只与信道的物理特征有关,与信道状态无关[14,15],在协作分集通信网络中节点间距离很小(β≤10-6s)。τ代表数据帧在节点的处理时间,这和节点的计算能力相关,与信道状态无关,所以可以设定为一个常数值。Tfk是指反馈信号从目的节点反馈到源节点的时间,假设反馈信息是无错传输的(可以加入足够的冗余位来保证),反馈信号数据量很小,在高速的无线传输系统中
假设调制编码模式是N种(包含 0模式就是N+ 1种),在模式0的情况下源节点不发送数据,本文设定0模式时数据帧等待一个时隙发送,则0模式的反馈延迟为一个时隙大小(Tf),N种调制编码模式对应有2N+1种反馈延迟。在n模式下由于数据帧传输路径不同造成的两种反馈延迟的概率如下:
直接链路S-D正确传输数据帧时反馈延迟T0的概率

直接链路S-D传输数据帧错误时,目的节点接收来自中继节点放大转发的数据帧时反馈延迟T1的概率
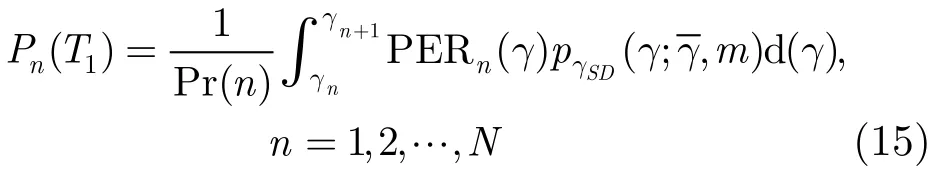
由第 3节对于信道模型的分析,得到了Nakagami-m信道状态之间的关系,我们用马尔科夫链{Sn}对信道状态进行描述,式(11)信道状态转移矩阵中任意两个状态都互通,并且对角线上元素不为0,{Sn}为一个不可约,非周期的马尔科夫链,则可知{Sn}存在稳态分布。本文中每一种信道状态对应有一种调制编码模式,N+1种调制编码模式的状态转移概率矩阵就是式(11)中的信道状态概率转移矩阵,显然N+1种调制编码模式就可以构成一个马尔科夫链{Tn},并且存在唯一的稳态分布。N种调制编码模式对应的反馈延迟的转移矩阵块为
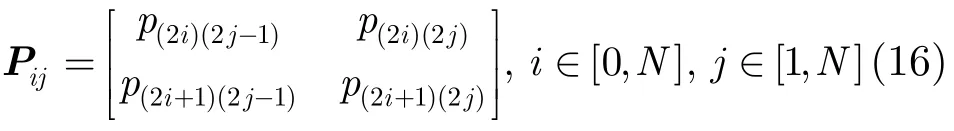
i,j分别表示调制编码模式。对于式(12)和式(13)两种反馈延迟在一次数据帧传输过程中是对立事件,则由式(11),式(14)和式(15)得到
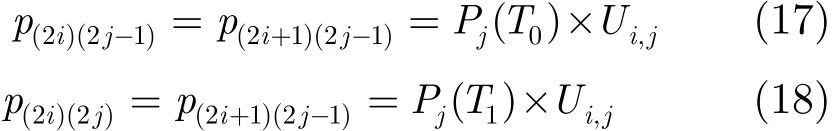
反馈延迟在0模式时,相邻时隙间调制编码模式保持不变的转移概率关系。
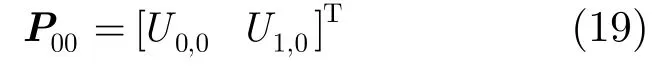
由式(8)-式(10)可得
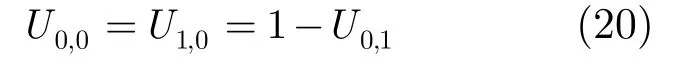
由式(16)-式(20)得到2N+1种反馈延迟的转移概率矩阵
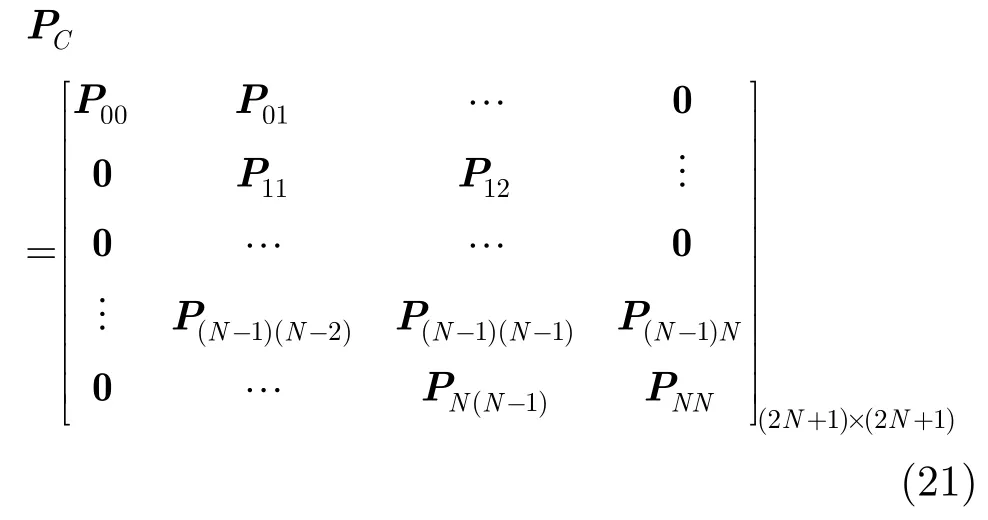
式(21)中2N+1种反馈延迟是由调制编码模式之间的转移关系得到的,每一个调制编码模式转移概率对应有两个子状态的转移关系矩阵块,由以上分析可知N+1种调制编码模式构成的马尔科夫链{Tn}存在稳态分布,则2N+1种反馈延迟存在稳态概率π={π0,π1,…,π2N)满足稳态方程:

由式(21)-式(23)得到2N+1种反馈延迟的稳态概率分布。
5 理论数值分析与仿真
对于第3节,第4节的理论推导进行数值分析和仿真比较研究。运用Matlab进行理论数值计算分析,采用蒙特卡洛仿真实验来验证理论计算的正确性,仿真时,结合文献[16]中Nakagami-m序列的构造,以及文献[17]中Nakagami-m衰落信道的仿真实现,构建三节点协作分集网络数据帧发送模型。设fd=3 Hz,Tf=2 ms ,数据帧大小Ns=1 080 bits ,信道衰落参数m=2,物理层最大误帧率Pmax=0.01,直接链路S-D平均接收信噪比取值从0 dB到40 dB时,选用表1中5种调制编码模式(N=5)进行分析研究[10]。为了描述简便,和分别表示反馈延迟是不同编码调制模式直接链路S-D正确接收到数据帧时(第1种情况)和直接链路S-D数据帧发送错误时数据帧通过中继链路S-R-D到达目的节点时的反馈延迟(第 2种情况)概率,u∈[0,5],v∈[1,5]分别表示调制编码模式。
图4是表1中5种调制编码模式下的概率分布理论计算和仿真对比曲线。可以看到在平均信噪比在2 dB,5 dB,8 dB,14 dB,21 dB时各调制编码模式对应的反馈延迟概率达到峰值。但是概率的数量级都在 1 0-4,那是由于直接链路S-D的最大误帧率Pmax=0.01较小,直接链路数据帧错误概率较小,那么通过中继链路传输数据帧反馈延迟的概率就较小。
图3和图4中的理论计算曲线与仿真曲线吻合良好,验证了本文对于AF协作分集网络中数据帧一次发送过程中反馈延迟的稳态概率分布推导分析模型的正确性。
图5是Nakagami信道的衰落参数m与的关系,实线是m取值为2时虚线是m取值为4时的分布关系比较,可以看到m增大,的概率曲线变化率增大,各种调制编码模式的反馈延迟概率峰值也变大。这是因为信道的衰落参数增加信道状态变好,直接链路S-D正确的概率变大,那么相应的增大,而就会相应变小。

图3的概率分布理论计算与仿真比较
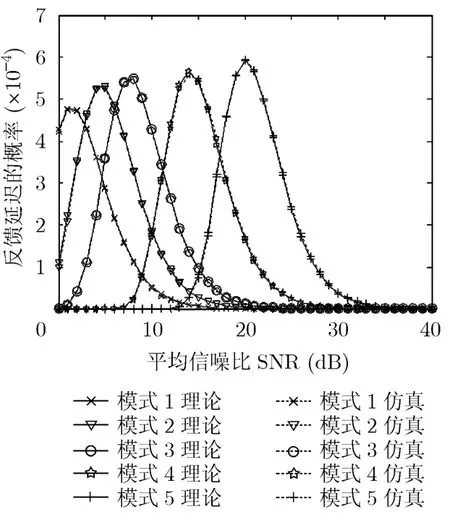
图4 的概率分布理论计算与仿真比较
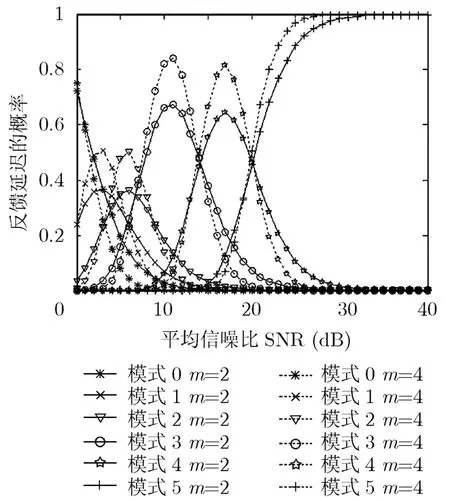
图5 信道衰落系数m与系数 的关系
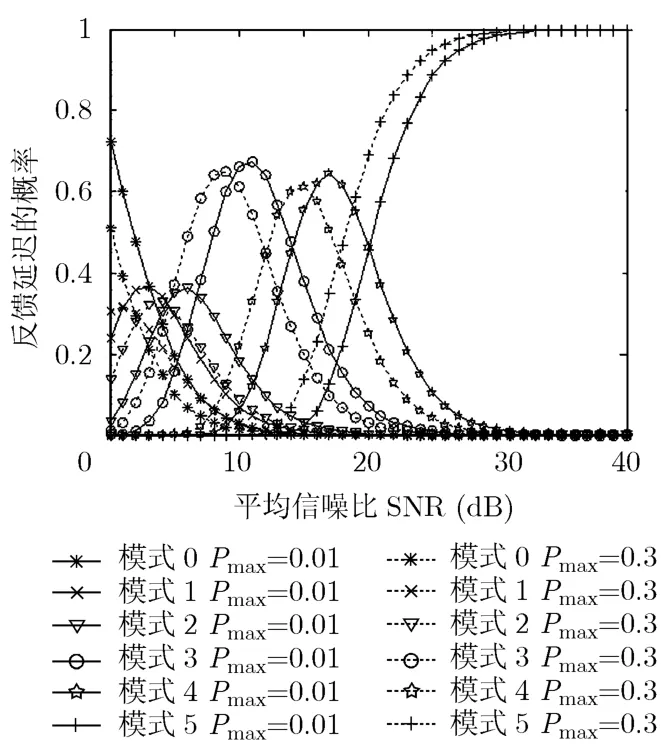
图6 最大误帧率Pmax与系的关系
6 结束语
本文介绍了协作分集技术,在协作分集三节点通信网络模型中,采用有限状态马尔科夫模型分析Nakagami-m分布衰落信道,研究了协作分集的物理层一个数据帧发送过程的反馈延迟的随机性。由于协作分集无线网络中中继节点的存在,数据帧传输路径多样性造成目的节点接收到数据帧的时间有多种,我们在协作分集网络 AF模式下简单认为是两种。在此基础上结合自适应编码调制技术分析数据帧的反馈延迟的随机性,得到反馈延迟的状态转移概率矩阵,进一步由马尔科夫链稳态方程得到反馈延迟的稳态概率,经过仿真实验结果与数值分析结果的对比,验证了推导分析模型的准确性,最后分析了信道衰落系数以及最大误帧率对于反馈延迟的影响。研究协作分集反馈延迟的随机性对于时延要求不同的无线业务的优化有重要的意义。本文研究只是针对 AF模式,在实际无线通信网络中中继节点也有数据要发送,那么源节点的数据帧在中继节点就存在排队过程[18],这对于数据帧发送的反馈延迟有影响。协作分集无线网络条件下采用DF模式时系统的性能更好,所以未来我们可以进一步研究中继节点的排队问题以及 DF模式的反馈延迟的随机性。
[1]Sendonaris A,Erkip E,and Aazhang B.User cooperation diversity-part I:system description[J].IEEE Transactions on Communications,2003,51(11):1927-1938.
[2]陈吉学,王文博.非再生中继Nakagami-m信道协同系统的性能分析[J].吉林大学学报(工学版),2009,39(1):225-228.Chen Ji-xue and Wang Wen-bo.Non-regenerative relay Nakagami-m channel collaborative system performance analysis[J].Journal of Jilin University(Engineering Science),2009,39(1):225-228.
[3]Laneman J N,Tse D N C,and Wornell G W.Cooperative diversity in wireless networks:efficient protocols and outage behavior[J].IEEE Transactions on Information Theory,2004,50(12):3062-3080.
[4]Krikidis I,Thompson J S,and McLaughlin S.On the diversity order of non-orthogonal amplify-and-forward over block-fading channels[J].IEEE Transactions onWireless Communications,2010,9(6):1860-1900.
[5]Li H and Zhao Q.Distributed modulation for cooperative wireless communications[J].IEEE Signal Processing Magazine,2006,23(5):30-36.
[6]Issariyakul T and Krishnamurthy V.Amplify-and-Forward cooperative diversity wireless networks:model,analysis,and monotonicity properties[J].IEEE/ACM Transactions on Networking,2009,17(1):225-238.
[7]Charash U.Reception through Nakagami fading multipath channels with random delay[J].IEEE Transactions on Communications,1979,27(1):657-670.
[8]Alouini M S and Goldsmith A J.Adaptive modulation over Nakagami fading channels[J].Wireless Communications,2000,13(1):119-143.
[9]Mardani M,Harsini J S,Lahouti F,et al..Joint adaptive modulation coding and cooperative ARQ over relay channels-applications to land mobile satellite communications[C].IEEE International Symposium on Wireless Communication Systems,Reykjavik,Iceland,October 21-24,2008:358-382.
[10]Liu Qing-wen,Zhou Sheng-li,and Giannakis G B.Cross-layer combining of adaptive modulation and coding with truncated ARQ over wireless links[J].IEEE Transactions onWireless Communications,2004,3(5):1746-1755.
[11]Wang H S and Moayeri N.Finite-state Markov channela useful model for radio communication channels[J].IEEE Transactions on Vehicular Technology,1995,44(1):163-171.
[12]Razavilar J,Liu K J R,and Marcus S I.Jointly optimized bit-rate/delay control policy for wireless packet networks with fading channels[J].IEEETransactionson Communications,2002,50(3):484-494.
[13]Shi Fei-jin and Yuan Dong-feng.Cross-layer combination of cooperative HARQ with AMC in wireless Ad hoc networks[C].IEEE Singapore International Conference,Guangzhou,China,November 19-21,2008:896-900.
[14]史斐谨.无线通信网络的跨层设计研究[D].[硕士论文],山东大学,2009.Shi Fei-jin.Cross-layer design of wireless communication network[D].[Master dissertation],Shandong University,2009.
[15]任孝锋,李建新.IEEE802.11WLAN中DCF延迟性能分析[J].信息工程大学学报,2009,10(2):181-183.Ren Xiao-feng and Li Jian-xin.Performance analysis of DCF delay in the IEEE802.11WLAN[J].Journal of Information Engineering University,2009,10(2):181-183.
[16]Zhang Q T.A decomposition technique for efficient generation of correlated Nakagami fading channels[J].IEEE Journal on Selected Areas in Communications,2000,18(11):2385-2392.
[17]Ma Yao and Zhang Dong-bo.A method for simulating complex Nakagami fading time series with nonuniform phase and prescribed autocorrelation characteristics[J].IEEE Transactions on Vehicular Technology,2010,59(1):29-35.
[18]Rong Bei-yu and Ephremides A.Protocol-level cooperation in wireless networks:stable throughput and delay analysis[C].Symposium on Modeling and Optimization in Mobile,Ad hoc,and Wireless Networks,Seoul,Korea,June 23-25,2009:1-10.

