形态学广义分形维数在发动机故障诊断中的应用

李 兵， 张培林， 任国全， 刘东升， 米双山

(1.石家庄军械工程学院 自行火炮教研室，石家庄 050003;2.石家庄军械工程学院 导弹机电工程教研室，石家庄 050003)

振动是发动机在运转过程中产生的必然现象，振动信号包含了发动机运行状态的丰富信息，发动机工作性能的变化可以通过振动信号表现出来，而其采集和分析不影响发动机的正常运转。因此，振动信号分析法成为对发动机进行结构、故障分析和状态监测最为广泛、也是最行之有效的方法［1]。

传统的故障诊断技术是针对振动信号的时域或频域特征来提取特征量进行故障识别的。但对于多部件、多激励的往复式发动机而言，由于其运动件多而复杂，工作条件恶劣，激励力众多且其频率范围宽广，各种激励经相应的传递及耦合均被反映在发动机表面的振动中，使得所测得的表面振动信号是极其复杂的混合信号［2，3]，用传统的理论方法去刻画这种复杂性具有很大的局限性。

分形几何为复杂信号提供了一种几何结构分析方法，它在很多领域已经有了成功的应用。在机械设备故障诊断领域中，人们也开始用分形几何方法对振动信号进行分析，并取得了一定的成果［4，5]。然而，在振动信号分析中，人们一般只考虑信号的单重分形特征，它只能从整体上反映信号的不规则性，缺乏对局部奇异性的刻画。多重分形维数能更精细的刻画信号的局部尺度行为，可以更加全面反映信号的分形特性。描述多重分形的主要方法有多重分形谱和广义分形维数两套参数体系，研究证明这两套参数体系之间存在着勒让德变换的关系，即已知一套参数即可计算出另一套参数，本文主要研究基于Renyi熵的广义分形维数的计算方法。

计算广义分形维数最常用的方法是覆盖法即盒计数法(Box-counting method)，这种方法有其不可避免的缺点，这主要是因为盒计数法采用了规则划分网格的方法，因此对分形维数的估计在某些情况下非常不稳定［6]。

针对盒计数法计算广义分形维数存在的缺点，本文提出了基于数学形态学操作的广义分形维数的计算方法，并对发动机正常、失火和气门间隙过大故障信号进行了分析，结果表明，基于数学形态学的广义分形维数可以非常有效的表征不同状态下发动机故障信号的特性。

1 多重分形维数

自从曼德尔布罗特在70年代提出分形概念以来，分形在物理、天文、地理、数学、计算机等科学领域取得了广泛的应用，并且取得了大量富有新意的成果。但是随着理论研究和应用的深入，研究者们越来越清楚地意识到，对于大多数客观存在的分形物体而言，仅用一个分形维数并不能完全刻画其结构。多重分形是定义在分形上的，由多个标量指数的奇异测度(即不存在测度密度的测度)所组成的集合。它刻画的是分形测度在支集上的分布情况，即用一个谱函数来描述分形不同层次的特征。这就是从形体的部分(小尺度)出发，根据自相似性质，研究其最终整体(大尺度)特征的理论基础。

描述多重分形的一种方法是广义分形维数，覆盖法是分形研究中最通用的方法，它既用于简单分形，也用于复杂分形。覆盖法就是用尺度为ε的相同大小的盒子对整个集合进行覆盖，所需盒子总数是N(ε)，设点落入第i个盒子的概率为Pi(ε)，对给定参数q，可计算出广义信息熵Kq(ε)的表达式为［7]

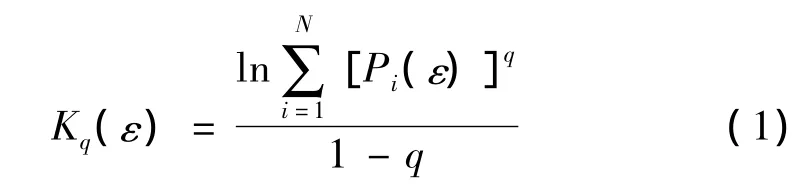
从而广义分形维数定义为

由于具有不同标度指数的子集可通过q的改变进行区分，当q=0时:

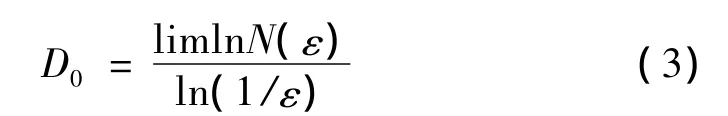
为容量维数(盒维数)。

当q=1时:

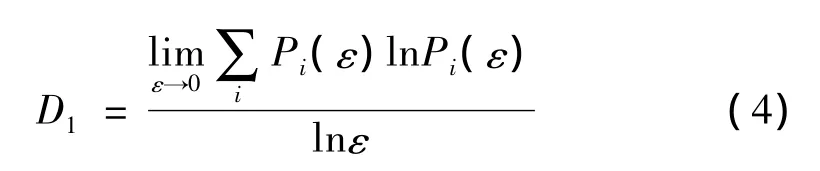
即为信息维数。

当q=2时，式(2)即为关联维数:

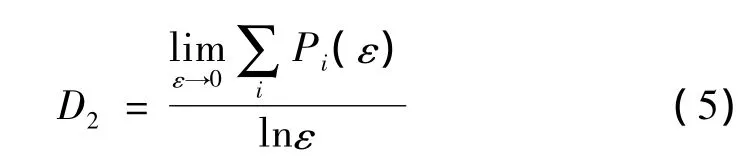
由此说明广义分形维数Dq包含了自相似分形理论涉及的大部分分形维数。

然而，由于盒维数的计算本质是对信号进行规则的网格划分，文献［8] 指出，这种规则的划分网格的方法必将会导致对所需盒子数估计的误差，从而影响分形维数估计的精度，而且误差相当可观。

为克服盒维数计算方法本质上的缺陷，必须寻找新的切入点来实现对分维数的精确估计。因此，本文提出了基于数学形态学的广义分形维数估计方法。

2 基于数学形态学的广义分形维数

数学形态学是以集合论、积分几何和拓扑学为基础发展起来的一种有别于时空域分析和频域分析的数学方法。它的基本思想是用具有一定形态的结构元素去度量和提取信号中的对应形态，以达到对信号进行分析和识别的目的。膨胀和腐蚀是数学形态学的两种基本运算，它们可以在保持信号的基本特征的前提下，去除信号中尺度上小于结构元的细节，从而得到结构简化的信号数据。这就如同在不同的尺度下观察信号，当使用尺度较小的结构元时，可以看到较多的细节如果换用尺度较大的结构元，看到的就只有粗的轮廓了。而各种分形维数估计算法的基本思想都是在不同尺度下对分形集合进行度量，而数学形态学正好为我们提供了一种在不同尺度下度量信号的数学工具［9]。所以，采用数学形态学来计算信号的分形维数应该是一个非常自然而恰当的选择。

2.1 数学形态学基本算子

数学形态学的基本运算包括腐蚀和膨胀两种算子。设f(n)和 g(m)分别为定义在 F={0，1，2，…，N －1}和 G={0，1，2，…，M －1}上的离散函数，且 N≫M。这里为f(n)输入信号，g(m)为结构元素。

f(n)关于g(m)的腐蚀定义为:

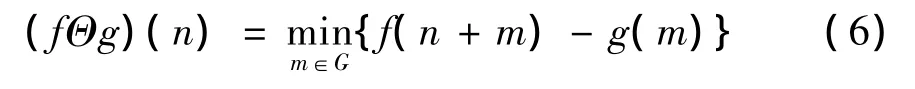
f(n)关于g(m)的膨胀定义为:

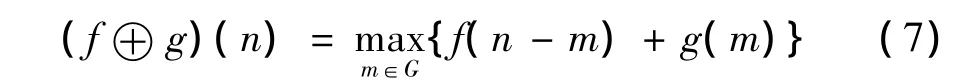
腐蚀和膨胀运算等价于离散函数在滑动滤波窗(相当于结构元素)内的最小值和最大值滤波。一般情况下，腐蚀运算减小了信号的峰值，加宽了谷域;而膨胀运算增大了信号的谷值，扩展了峰顶，关于数学形态学更加详细的理论描述可参考文献［10，11] 。

2.2 基于数学形态学的单一分形维数估计

文献［8] 提出了基于数学形态学的单一分形维数估计方法，其主要计算过程如下。

假设信号为f，g单位结构元素，定义尺度ε下的结构元为:

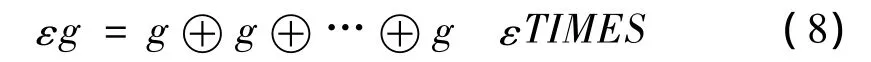
则在不同尺度ε下对信号f的膨胀和腐蚀分别为f⊕εg(n)和 fΘεg(n)。其中 ε =1，2，…，εmax，且 εmax≤N/2。

根据文献［8] 的方法，选择g为长度为3的扁平结构元素，即g={0，0，0}，选择扁平结构元素的好处是可以减少一部分计算量。

定义尺度ε对信号的覆盖面积为:

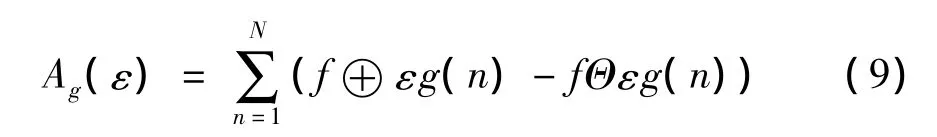
文献［8] 证明各尺度下Ag(ε)满足:

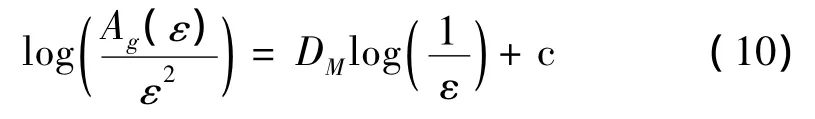
则DM可由下式求得:

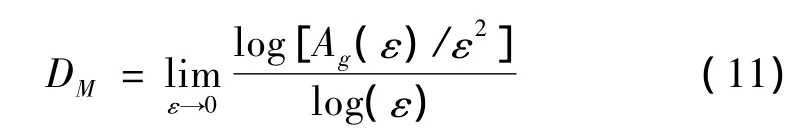
实际计算中对 log(Ag(ε)/ε2)和 log(1/ε)进行最小二乘线性拟合得到对信号分形维数DM的估计。

2.3 数学形态学的广义分形维数估计

由前述的在不同尺度ε下对信号f的膨胀和腐蚀分别为f⊕εg(n)和 fΘεg(n)，我们可以定义一个反映局部度量的分布函数ui(ε):

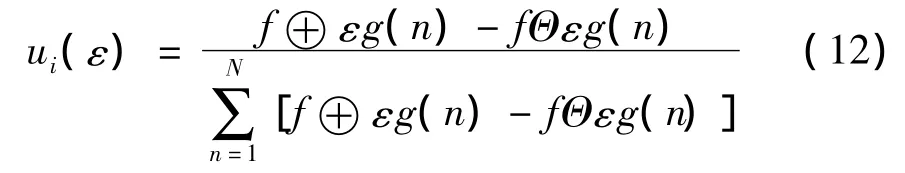
很显然，上式中的 f⊕εg(n)－fΘεg(n)表示了信号膨胀结果与腐蚀结果之间的差异，其作用就像是单个网格上所需的盒子数，分布函数ui(ε)则描述了这种差异的分布，信号在尺度上的不均匀性可以通过分布函数的高阶矩所表现出的奇异性来刻画。

对给定参数q，可计算出形态学广义信息熵Kq(ε)的表达式为:

由式(12)可以看出，基于数学形态学的网格划分是固定的，即所有尺度下的网格数均为信号的点数N(ε)=N。如果采用计盒方法计算信号的覆盖面积，Ag(ε)相当于盒子数 N(ε)与单位盒子面积 ε2的乘积，则:

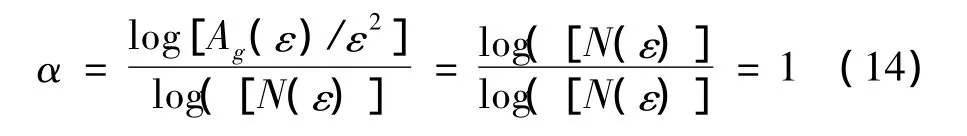
从而保证了与广义信息熵式(1)描述的一致性。

作为一个多重分形度量Kq(ε)与尺度之间必定满足如下所示的指数关系:

则基于数学形态学的广义分形维数可由下式求得:

实际计算中对Kq(ε)和log(ε)进行最小二乘线性拟合得到对广义分形维数Dq的估计。

可以证明当 q=0 时，K0(ε)= － log(Ag(ε)/ε2)，则多重分形维数Dq退化为基于数学形态学的单一分形维数。

3 发动机故障信号分析

实验在F3L912型三缸四冲程柴油机上进行，加速度传感器粘贴在第一缸缸盖处，实验在空间较大的车间内进行，计算机、电荷放大器等装置在车间里的控制间内放置。发动机故障设置为一缸失火和进气门间隙过大两种故障。实验时发动机转速为1 200 r/min，采样频率为40 kHz，采样点数为发动机一个工作周期。

图1 发动机三种状态下振动加速度信号时域波形图Fig.1 Waveform of vibration signal from engine with three states

图1为发动机在正常、失火和进气门间隙过大三种状态下的时域波形图。从图中可以看出，三种状态下缸盖振动加速度信号的时域波形具有较明显的差异。失火时，燃爆信号消失，进气门间隙过大时，进气门关闭响应明显变大。

以进气门间隙过大时的信号为例说明基于数学形态学的分形维数计算方法，图2为采用不同尺度的结构元素对信号进行形态学变换的结果。其中实线为采用尺度为20的扁平结构元、虚线为采用尺度为100的扁平结构元运算结果。

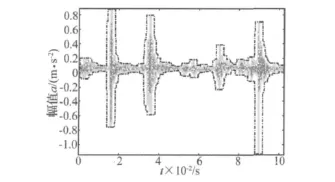
图2 发动机气门间隙故障信号及其腐蚀、膨胀图Fig.2 Dilation and erosion waveform of the vibration signal from engine with valve fault

本文选择分析信号的单位结构元素g为长度为3的扁平结构元素，即 g={0，0，0}，最大尺度为100，即εmax=100，参数q取值范围为［－20:2:20] ，然后根据2.3所描述方法计算信号的广义分形维数。图3给出了采用数学形态学操作所计算的进气门间隙过大故障信号的广义分形维数图。从图中可以看出，信号的广义分形维数Dq随q呈严格的递减，当q=0时Dq就退化为基于数学形态学的单一分形维数。

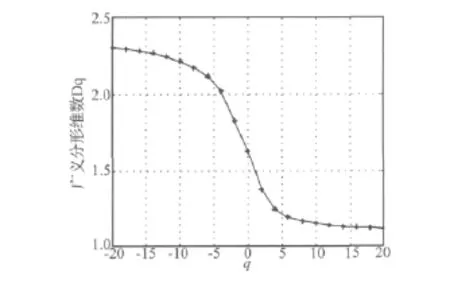
图3 发动机气门间隙故障信号的形态学广义分形维数Fig.3 Morphological generalized fractal spectrum of signal from engine with valve fault

图4 为采用数学形态学方法计算的发动机三种状态下振动信号的广义分形维数谱，每种状态取样本数为4。

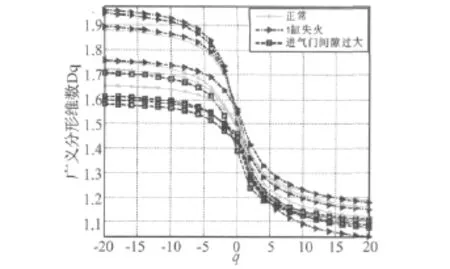
图4 发动机三种状态下信号广义分形维数(盒计数法)Fig.4 Generalized fractal spectrums of signals from three engine states using box－counting method

从图中可以看出，在q=0时即采用单一的分形维数很难将三种状态进行区分;在q＜0时三种状态的分形维数存在着很大的混叠，完全不可分;但是当q＞0，三种状态的分形维数可以进行明显的区分。这说明了采用单一的分形维数包含的信号奇异性信息十分有限，在部分情况下很难对不同状态的信号进行区分，而广义分形维数可以在不同的层次上对信号的奇异性进行分析，因此采用广义分形维数对复杂信号进行分析具有很大的优越性和必要性。

同时，本文还采用传统的盒计数法计算了发动机在三种状态下的广义分形维数。在计算中，盒子的尺度选择为［2，4，8，16，32，64，128，256，512] 个采样点。图5给出了相应的广义分形维数谱，与图4相比可以发现，盒计数法计算的广义分形维数对发动机的三种状态区分性较差，不利于对发动机故障状态进行分类。

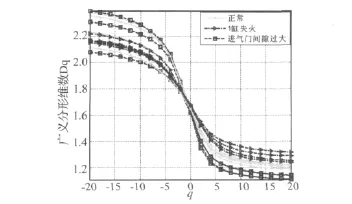
图5 发动机三种状态下信号的形态学广义分形维数Fig.5 Morphological generalized fractal spectrums of signals from three engine states

5 结论

数学形态学为数字信号处理提供了一种新的快速分析手段，本文提出了一种基于数学形态学的广义分形维数计算方法，并证明了与盒计数法计算广义分形维数的一致性。通过对实际的发动机正常、失火故障和气门间隙过大故障振动加速度信号的分析结果表明，与传统的盒计数方法相比，基于数学形态学计算方法的广义分维数估计能够更加准确的将不同状态下的发动机振动加速度信号进行区分，可以有效的用于发动机故障状态的判别。此外，数学形态学只涉及简单的加减和取大取小运算，因此与传统的盒计数方法相比，基于数学形态学的广义分形维数计算效率更高，为发动机故障特征提取和故障诊断提供了一种更为快速、有效的分析方法。

［1] Wu J D，Chen J C.Continuous wavelet transform technique for fault signal diagnosis of internal combustion engines［J] .NDT and E International，2006，39(4):304 －311.

［2] 金 萍，陈怡然，白 烨.内燃机表面振动信号的性质［J] .天津大学学报(自然科学与工程技术版)，2000，33(01):63－68.

［3] 夏 勇，张振仁，陈卫昌，等.分形维数在内燃机振动诊断中的应用［J] .振动、测试与诊断，2001，21(03):209－212.

［4] 李 娜，方彦军.利用关联维数分析机械系统故障信号［J] .振动与冲击，2007，26(4):136－139.

［5] 胥永刚，何正嘉.分形维数和近似熵用于度量信号复杂性的比较研究［J] .振动与冲击，2003，22(03):25－29.

［6] Chaudhuri BB，Sarkar N.Texture segmentation using fractal dimension［J] .IEEE Transactions on Pattern Analysis and Machine Intelligence，1995，17(1):72－77.

［7] Grassberger P.Generalized dimensions of strange attractors［J] .Physics Letters A，1983，97(6):227－230.

［8] Maragos P，Sun F K.Measuring the fractal dimension of signals:morphological covers and iterative optimization［J] .IEEE Transactions on Signal Processing，1993，41(1):108－121.

［9] Radhakrishnan P，Lian T L，Daya Sagar B S.Estimation of fractal dimension through morphological decomposition［J] .Chaos，Solitons and Fractals，2004，21(3):563 －572.

［10] Maragos P，Schafer R W.Morphological filters-PartⅠ:Their set-theoretic analysis and relations to linear shiftinvariant filters［J] . IEEE Transactions on Acoustics，Speech，and Signal Processing，1987，ASSP － 35(8):1153－1169.

［11] Maragos P，Schafer R W.Morphological filters-PartⅡ:their relationsto median，order-statistic，and stack filters［J] .IEEE Transactions on Acoustics， Speech， and Signal Processing，1987，ASSP－35(8):1170－1184.