基于进化蒙特卡洛方法的特征选择在机械故障诊断中的应用

刘晓平， 郑海起， 祝天宇

(1.军械工程学院，石家庄 050003;2.武汉军械士官学校，武汉 430075)

机械故障诊断是一个典型的模式分类问题。首先，通过安装在机械设备上的各类传感器提取该设备的运行信息。然后，利用各种信号处理方法进行分析处理，形成原始特征集。最后，将特征集作为分类器的输入，达到故障分类的目的。然而，在实际的故障诊断中，原始特征集中常常包含冗余特征，导致计算量的加大以及分类精度的降低。因此，研究如何寻找最优的特征子集，提高诊断精度是一个有重要意义的课题［1，2]。

在实际应用中，寻找最优的特征子集通常是很难的，高维数据情况下特征选择问题通常是 NP难问题。因此只能通过非穷尽搜索算法在运算效率和特征子集质量间折中考虑。遗传算法、模拟退火等非穷尽式随机搜索算法在特征选择中已有了较多的研究［3，4]。然而传统的遗传算法易于过早收敛和陷入局部极小。在模拟退火中，任何比对数下降快的降温方式都不能保证算法收敛到全局最优点，而足够慢的降温过程又导致了极低的搜索效率。

进化蒙特卡洛(EMC)［5，6]是一种基于总体的蒙特卡洛方法，它联合了遗传算法与模拟回火各自的优点。运用遗传算法中变异和交叉的思想指导马尔可夫蒙特卡洛移动，是一种具有“学习”能力的蒙特卡洛方法。研究表明，进化蒙特卡洛对于高维分布采样模拟和优化问题是非常有效的［7－9]。

将进化蒙特卡洛方法引入机械故障诊断的特征选择，采用支持向量机(SVM)作为分类决策器，Wrapper式特征子集评价标准，利用进化蒙特卡洛算法搜索最优特征子集。以滚动轴承振动信号特征选择为例，验证了方法的有效性。

1 进化蒙特卡洛算法

进化蒙特卡洛(EMC)是一种基于总体的蒙特卡洛方法，它将遗传算法中的变异和交叉运算引入到模拟回火的框架，运用变异和交叉的思想指导马尔可夫蒙特卡洛移动。它同时运行多条马尔可夫链，每一条链均与固定的温度相联系。这些链通过变异、交叉和交换操作来更新［5，6]。假设目标分布为:

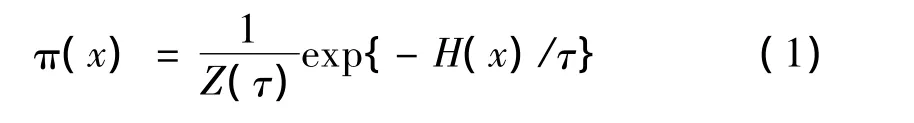
在EMC中，为了从上述目标分布中模拟抽样，首先建立N个Boltzmann分布:

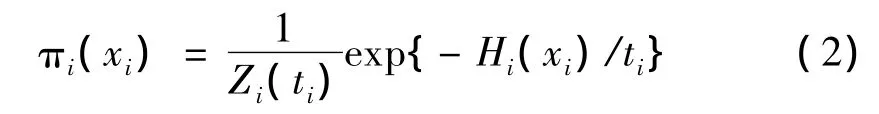
其中Zi(ti)是该分布的归一化常数。

T=(t1，t2，t3，…，tN)是 N 个给定的不同温度值，并且t1＞t2＞t3＞…＞tN=τ，这样(·)就是采样的目标分布。用xi表示从(xi)中的一个采样，x1，x2，…，xN组成一个总体X，其中N表示总体的容量，X={x1，是一个d维的向量，称为个体或染色体。在EMC中，应用的是增广状态空间X上的马尔可夫抽样。目标分布为总体的Boltzmann分布:

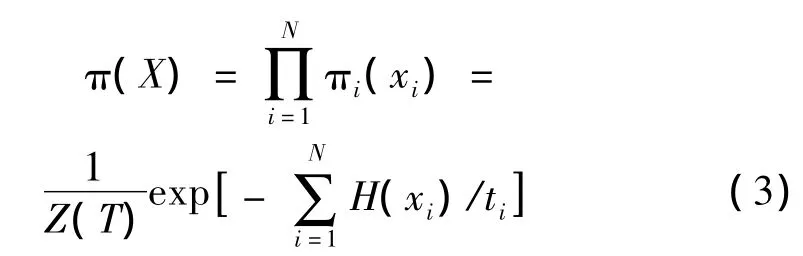
1.1 变异

在变异操作中，从当前总体X中随机选取一个染色体xk，在xk的二值序列的一个随机位置上随机改变其值，将xk变异为 yk。新的建议总体为 Y={x1，…，yk，…xN}。根据 Metropolis准则，以概率 min(1，rm)接受建议总体。在变异操作中，总体中的每个染色体都独立进行变异:

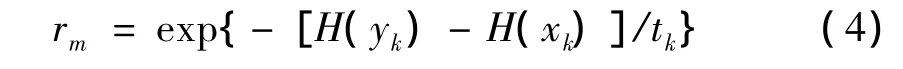
1.2 交叉

在交叉操作中，根据某种选择方式(例如随机选择或轮盘赌)，从当前总体X中选取一个染色体对xi和xj，新的后代yi和yj通过一次交叉运算获得。一个新的建议总体为 Y={x1，…，yi，…，yj，…xN}，根据 Metropolis准则，以概率min(1，rc)接受建议总体。

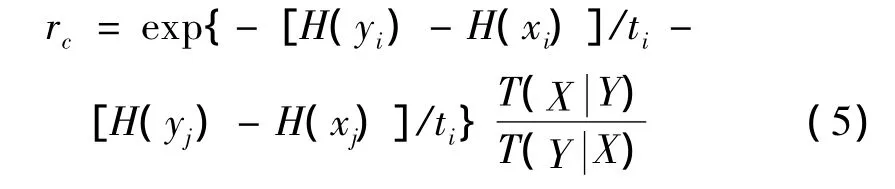
建议转移函数为:

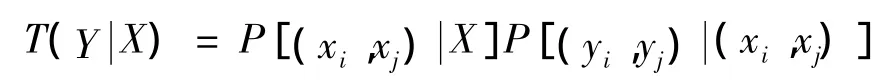
父辈染色体的选择方法如下:首先按照轮盘赌的方式以Boltzmann权重选出第一个染色体xi，即以概率选出xi。第二个染色体xj从剩余的总体中随机的选取。选中(xi，xj)的概率为:

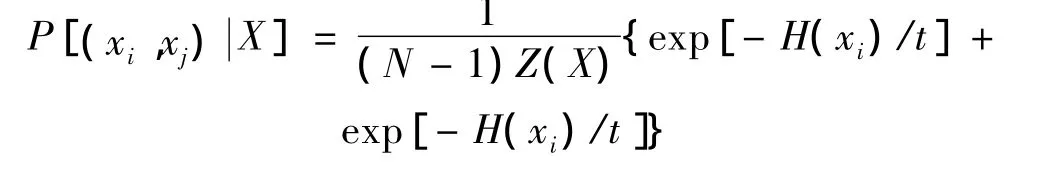
交叉运算可以选择在遗传算法中常用的1点交叉、2点交叉和均匀交叉。这些交叉都是对称的，即:

还有一种新的交叉运算:自适应交叉。在自适应交叉运算中，两个后代的产生方法如下。若xi和xj在它们的二值序列的第k个位子上的值相等，则后代yi和yj复制该值，并且独立地以概率p0改变该值;若xi和xj在它们的二值序列的第k个位子上的值不相等，则yi复制xi的值并以概率p2改变它，yj复制xj的值并以概率p1改变它。通常有0＜p0≤p1≤p2＜1，这种自适应交叉可以将一个总体好的基因型保存下来，同时算法的学习能力也加强了。在交叉操作中，通过迭代的方式约40%的染色体被选中进行交叉。

1.3 交 换

交换操作和并行回火［10]是一样的，给定当前总体X 和温度阶梯 T，(X，T)=(x1，t1，…，xN，tN)，在 xi和 xj之间进行一个交换操作但不改变温度阶梯，即初始状态为:

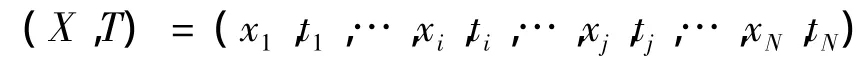
交换之后的状态为:

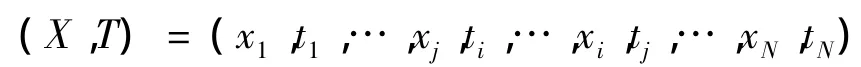
根据Metropolis准则，以概率min(1，re)接受建议总体。

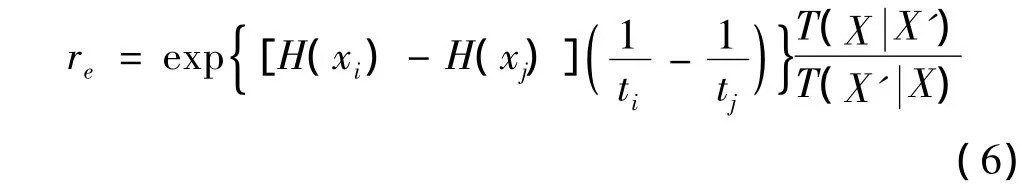
2 基于二值编码EMC的特征选择方法

特征选择的目的是从原始特征集中选择一个特征子集。这个子集对于一个评价函数来说是最优的。因此，特征选择是个最优化过程。特征选择需要解决两个问题:①特征子集的评价准则;②采用何种寻优策略来找到满足条件的最优子集。本文采用Wrapper模型，以学习算法的性能作为特征选择的评估标准。利用二值编码的进化蒙特卡洛作为搜索策略寻优特征子集。

2.1 解的表示方法

假设通过特征提取共得到了d个故障特征，那么特征集的维数为d。在特征选择问题中，一个特征要么在解中要么不在解中，因此，对解采用0和1的二进制编码。在二值编码的EMC中，每个染色体xi可用一个长度为d的0、－1二值序列表示，0表示对应的特征没被选中，1表示对应的特征被选中。

2.2 适应度函数的设计

以特征子集学习训练得到的分类错误率作为适应度函数，为了尽可能减小输入数据维数，采用如下适应度函数:

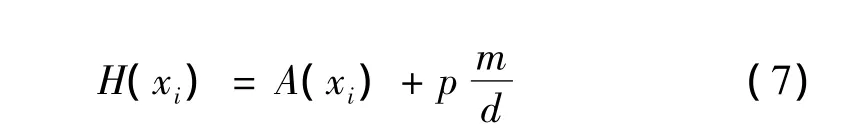
A(xi)为特征子集的分类错误率估计值;m为选中的变量数;d为原始特征数;p为调整参数，平衡最小错分率与选中特征个数。

采用交叉验证法(Cross-validation)来估计分类器的错误率。用支持向量机作为学习分类器对特征样本进行训练并估计特征集的分类错误率。支持向量机是Vapnik等人［11]根据统计学习理论提出的一种机器学习方法。统计学习理论是目前针对小样本统计估计和预测学习的最佳理论。支持向量机具有较强的泛化能力，能够收敛到全局最优，有效地克服了“维数灾难”，现已在机械故障诊断中得到广泛的应用［1，12]。

2.3 二值编码的EMC特征选择步骤

特征选择是一个优化问题，我们可以通过在特征子空间上的形式分布中抽样:

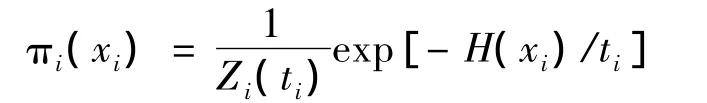
从而将优化问题转化为模拟问题。H(xi)是xi的适应度。二值编码的EMC可以用来从上述模型中进行抽样:

① 选择一个容量为N的总体X和温度阶梯T，随机初始化X;

② 计算每个染色体的适应度;

③ 以概率qm对总体进行变异，或以概率1－qm对总体进行自适应交叉;

④ 进行交换操作。在总体中随机的选取xi，以概率选取

⑤ 若算法终止准则满足，则停止。否则，返回步骤②。

3 实验结果分析

实验中采用减速机输入端6206轴承，在不影响轴承正常使用性能的情况下，分别在滚动轴承外圈和内圈加工宽为0.5 mm，深为1.5 mm的小槽来模拟轴承的局部裂纹故障。实验时测试系统为LMS多分析仪，振动传感器为B＆K4508，采用两路传感器采集信号，测点1位于轴承座，测点2位于齿轮箱体上。采样频率为8 192 Hz。分别在输入轴转速为600 r/min和1 200 r/min两种工况下进行采样，每种工况重复采样40次，实验中轴承共有3种工作状态:① 正常;② 外圈故障;③ 内圈故障。选择一半数据进行训练，其余数据用于测试。在训练阶段采用5折交叉验证。

对每一组轴承原始振动信号数据分别从时域统计、EMD分解提取特征。选取无量纲参数峰值因子、斜度因子、波形因子、脉冲因子、裕度因子及峭度因子等6个时域统计量为特征参数。使用EMD方法对原振动信号进行分解［12]，选择包含有用信息的前8个本征模式分量进行研究。分别计算各本征模式分量的能量，得到8个能量值，对本征模式分量矩阵进行奇异值分解，得到8个奇异值。

将上述提取的特征进行归一化处理。用x={β1，β2，…，βi，…，βd}表示原始特征集，每个测点信号依次提取上述时域特征、能量值、奇异值等22个特征，这样两路传感器共提取44个故障特征，x的维数就为44。图1～图4分别为其中一组外圈、内圈故障时的振动信号及EMD分解。

EMC的初始设置为:初始种群数N=20，温度在10和0.5 之间等间隔分布，变异率 qm=0.15，p0=0.02，p1=0.06，p2=0.1，最大迭代次数为 1 000。

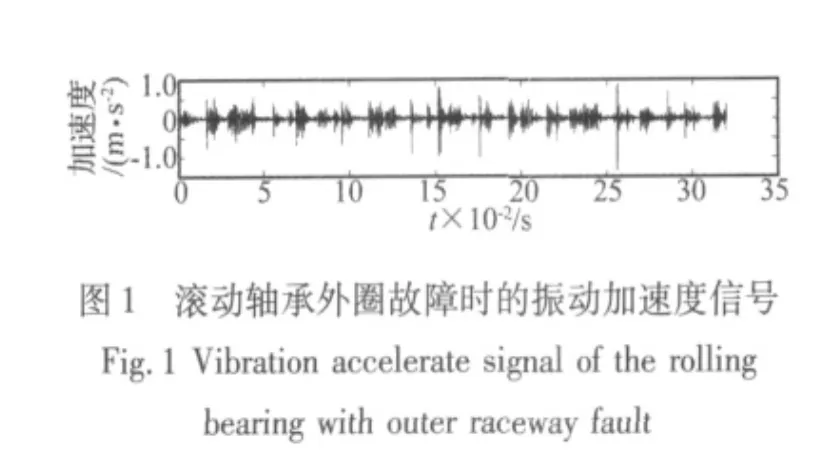
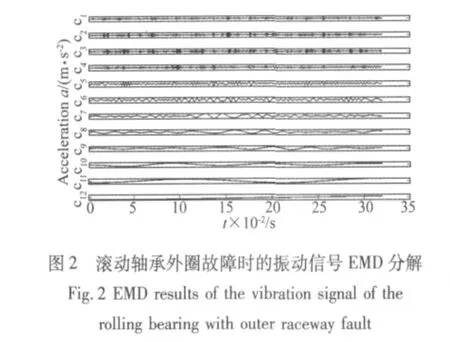
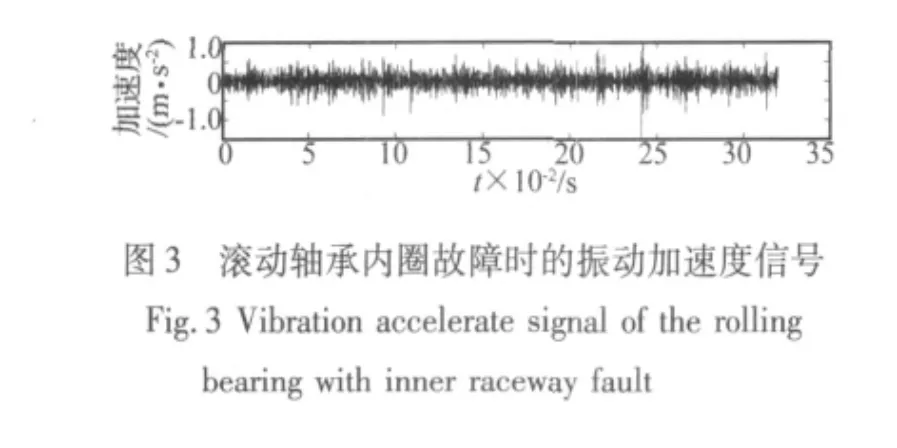
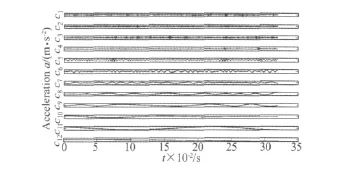
图4 滚动轴承内圈故障时的振动信号EMD分解Fig.4 EMD results of the vibration signal of the rolling bearing with inner raceway fault

图5 为外圈故障时各个特征被选择的概率。最后找到6个特征，寻优特征子集的维数为6，它们被选择的概率均大于0.8，分别是测点1的斜度因子、峭度因子、前两个IMF能量值及奇异值。图6为内圈故障时各个特征被选择的概率。最后找到7个特征，寻优特征子集的维数为7，它们被选择的概率均大于0.7，分别是测点1的斜度因子、峭度因子、第2、3个IMF能量值及前三个奇异值。

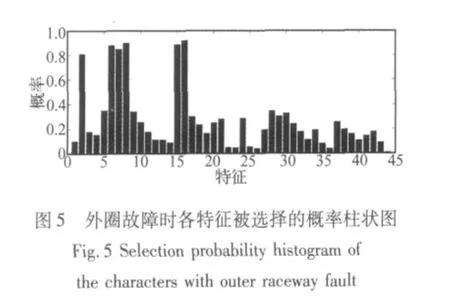
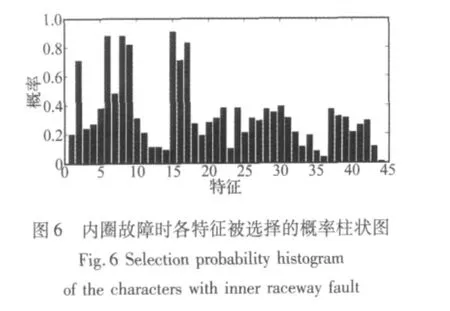
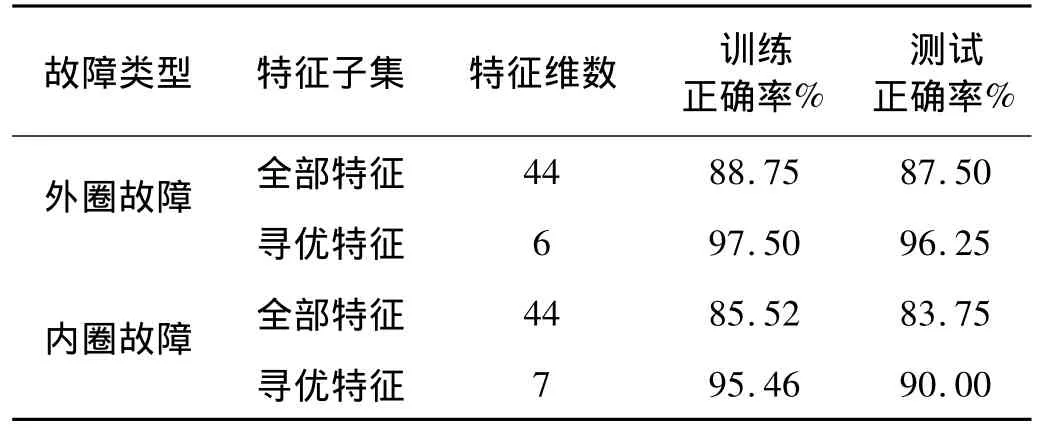
表1 不同特征子集SVM分类结果Tab.1 Classification results of SVM with different feature subset

为检验该方法的有效性，使用SVM分类器对原始特征集和优化子集的分类性能进行比较，结果如表1所示。由表1可知，经EMC算法搜索到的优化特征子集提高了SVM的分类精度。同时，经过特征选择后，大大降低了SVM输入向量的维数及其复杂度，提高了SVM的训练效率。

4 结论

针对在机械故障诊断中，由于原始特征集中冗余特征的存在，影响了诊断性能和效率，将进化蒙特卡洛方法引入机械故障诊断的特征选择，采用二值编码的EMC作为搜索策略从模型中进行抽样，利用特征子集对SVM分类性能的影响作为特征集的评价标准。实验表明，该方法能够从原始特征集中找到优化特征子集，提高故障诊断精度和效率。

［1] 王新峰，邱 静，刘冠军.基于灵敏度分析的支持矢量机特征选择［J] .机械工程学报，2006，42(4):122－126.

［2] 潘宏侠，黄晋英，毛鸿伟，等.基于粒子群优化的故障特征提取技术研究［J] .振动与冲击，2008，27(10):144－147.

［3] Wang X F，Qiu J，Liu G J.New feature selection method in machine fault diagnosis［J] .Chinese Journal of Mechanical Engineering，2005，18(2):251－254.

［4] Lin SW，Lee Z J，Chen SC，et al.Parameter determination of support vector machine and feature selection using simulated annealing approach ［J] .Applied Soft Computing，2008，8:1505－1512.

［5] Liang F，Wong W H.Evolutionary monte carlo:applications to cpmodel sampling and change point problem［J] .Statistica Sinica，2000，10(2):317－342.

［6] Liang F，Wong W H.Real-parameter evolutionary monte carlo with applications to bayesian mixture models［J] .Journal of the American Statistical Association，2001，96(454):653－666.

［7] Liang F，Wong W H.Evolutionary monte carlo for protein folding simulations［J] .Journal of Chemical Physics，2001，115(7):3374－3380.

［8] Goswami G，Liu J S，Wong W H.Evolutionary monte carlo methods for clustering［J] .Journal of Computational and Graphical Statistics，2007，16(4):1 －22.

［9] Goswami G，Liu J S.On learning strategies for evolutionary monte carlo［J] .Stat Comput，2007，17:23 －38.

［10] Wang C M，Hyman J D.Allon percus，russel caflisch.parallel tempering for the traveling salesman problem［J] .International Journal of Modern Physics C，2009，20(4):539－556.

［11] Vapnik V.Statistical learning theory［M] .New York:Wiley，1998.

［12] 程军圣，于德介，杨 宇.基于内禀模态分解奇异值分解和支持向量机的故障诊断方法［J] .自动化学报，2006，32(3):476－480.