钢纤维混凝土动态抗拉强度的实验研究

王 林，胡秀章，黄焱龙，李永池

(中国科学技术大学 近代力学系，合肥 230027)

诸如岩石、混凝土、陶瓷等材料，它们的抗拉强度远小于其抗压强度，具有明显的拉压不等性。如混凝土材料，其抗拉强度仅为抗拉强度的 0.07 ～0.11［1]，这也就导致了混凝土材料在承受远小于其抗压强度时经常出现拉伸破坏而无法充分发挥材料强度。另外，混凝土层裂(spalling)是混凝土建筑物或地下工事等遭遇爆炸等冲击荷载时的一种常见破坏现象。早年Komlos［2]、Takeda 与 Tachikawa［3]采用直接拉伸测试技术对混凝土材料的抗拉强度进行了实验研究。采用圆盘劈裂实验技术，Cowell［4]、Wakabayashi［5]等的实验结果表明混凝土材料的抗拉强度随应变率增加而提高。John［6]采用动态劈裂方法得出混凝土动态抗拉强度为准 静 态 时 的 4.8 倍。 Mellinger 与 Birkimer［7]、Birkimer［8]、McVay［9]、Ross［10]和 Antoun［11]等采用层裂测试实验技术对混凝土材料的动态抗拉强度进行了研究。作为一种广泛使用的高强度建筑材料，研究钢纤维混凝土材料的抗拉性能，尤其是其在动态荷载作用下的抗拉强度，对提高材料使用效率、充分发挥材料强度具有十分重要的工程意义。

1 钢纤维混凝土长杆层裂实验

1.1 试件配合比与基本力学性能

3种不同钢纤维体积率混凝土配合比见表1，配料中，水泥为洛阳中和“香山“牌PO425普通硅酸水泥;粗骨料为洗净连续粒级碎石，最大骨料粒径为10mm;细骨料为洗净伊河河沙，细度模数2.3，为中沙，颗粒级配属于级配Ⅱ区;所用拌和水为饮用自来水;减水剂为安徽精汇化工的SM高效减水剂;钢纤维为赣州大业金属纤维有限公司0213型微钢纤，纤维直径d=0.2 mm，长度l=15 mm(长径比l/d=75)。为了解材料的基本力学性能，我们进行了立方体抗压强度和圆盘劈裂实验，钢纤维体积率Vf=0、0.75%和1.50%试件立方体抗压强度依次为 62.7 MPa、66.7 MPa 和 68.6MPa，劈裂强度依次为 3.9 MPa、5.5 MPa 和 6.3 MPa，其中，立方体抗压强度实验加载应变率为 3.0×10－5s－1，劈裂强度实验加载应变率为1.0 ×10－6s－1。

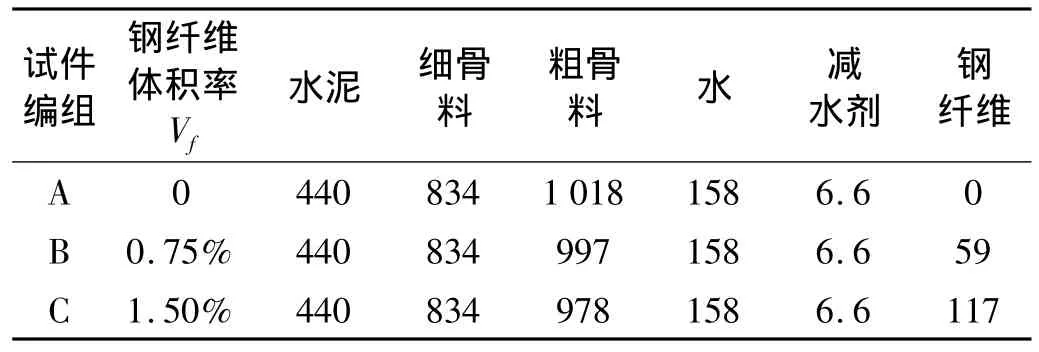
表1 钢纤维混凝土配合比(kg/m3)Tab.1 Mix proportion of SFRC(kg/m3)

1.2 实验原理

Díaz-Rubio在文献［12] 中提出了一种用于测试陶瓷和金属材料动态抗拉强度的方法。如果在有限长杆一端输入压缩应力波，该应力波沿杆向前传播在自由面反射为一反向的拉伸应力波后，入射压缩波与反射拉伸波相互作用，在邻近自由面附近产生相当高的拉应力，当此拉应力达到材料的动态抗拉强度，便在此处发生层裂现象而破坏。

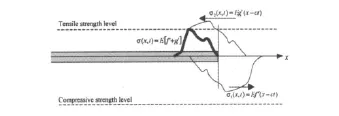
图1 应力波在自由端反射Fig.1 Reflection of a wave in free end

由一维应力波理论可知波的运动方程为:

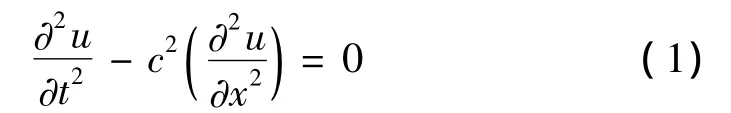
其中:u为质点位移;t为时间;x为质点长度坐标;c为纵波波速。积分式(1)可得微分方程的解:

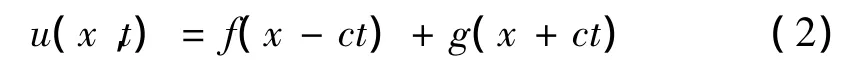
其中:f(x－ct)为沿x轴正向的应力波;g(x+ct)为反向应力波。

质点应变由下式直接求得:

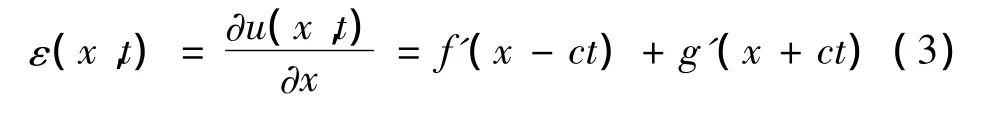
考虑到脆性材料抗拉强度远小于其抗压强度，因而可假定有线弹性应力－应变关系，即:

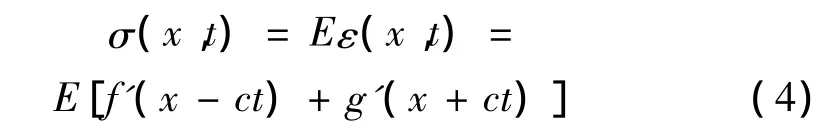
假设弹性压缩波沿着一半无限长杆向前传播，此时，函数f为压缩应力波，函数g为零(即没有反射波)。对于有限长杆，在自由端须满足σ=0的应力边界条件，因而有:

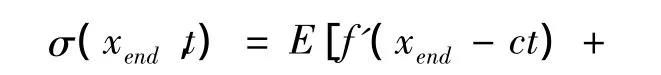
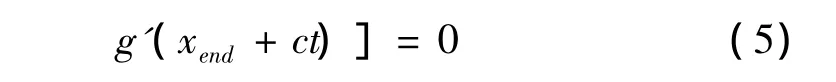
即:

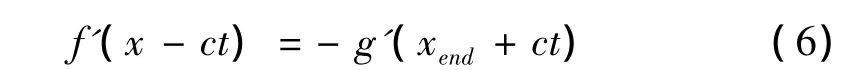
式(6)表明，在自由端压缩应力波反射一波形相同方向相反的拉伸应力波。

压缩波在自由端反射形成拉伸波只是一个前提，能否发生层裂还要取决于是否满足某种动态断裂准则［13]。这里我们采用最大拉应力瞬时断裂准则，按此准则，一旦拉应力σt达到或者超过材料的动态抗拉强度 σt，d，即 σt≥σt，d时，材料即发生断裂而破坏。

需要强调指出的是，该方法包含两个假定:① 材料为线弹性力学行为，即具有很小的拉压比(抗拉强度/抗压强度)，这样混凝土材料在承受压缩脉冲时不会发生破坏;② 一维应力波有效，此处半无限长杆的前提并非是必须的。只要长径比足够大，即可近似为一维应力波，其运动方程便可由式(1)表示［14，15]。

1.3 实验描述

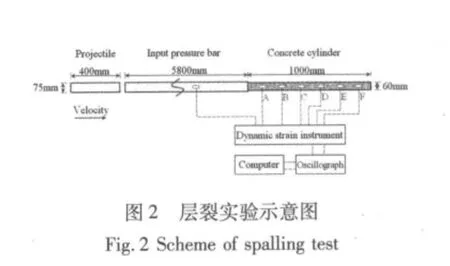
我们对三种体积率钢纤维混凝土试件进行了层裂实验研究，试件为Φ60 mm×1 000 mm(l/d=16.7)的杆状试件。实验在炮兵学院先进材料动力学实验室Φ75 mmSHPB实验系统上进行，示意图如图2。实验系统由子弹、入射杆和混凝土杆试件组成，通过调整支座，使得子弹、入射杆和混凝土试件轴线位于同一直线上。杆弹由高压气体驱动撞击入射杆，产生的压缩应力波沿杆向前传播到达入射杆/试件界面，部分应力波进入混凝土试件，应力波在试件自由端反射形成拉伸应力波，当杆中拉伸应力超过混凝土动态抗拉强度时，试件即产生层裂(图3)，子弹撞击速度为6.23 m/s－11.28 m/s。为记录应变信号，沿试件表面相隔一定间距对称粘贴应变片(图4)，用以消除试件表面因裂纹、孔洞等缺陷对应变信号造成的影响。

2 实验结果及分析

文献［12] 指出该方法只适用于陶瓷或金属等小尺寸试件，对于混凝土材料，必须考虑试件因大直径引起的波形弥散和幅值衰减现象。图5为试件不同位置处应力波形，可以看出，波形的几何弥散效应并不明显，在此，我们忽略了波形的几何弥散效应。但应力沿杆长存在幅值衰减，此处我们定义应力衰减系数α，表示相距一定距离应力幅值的衰减程度。

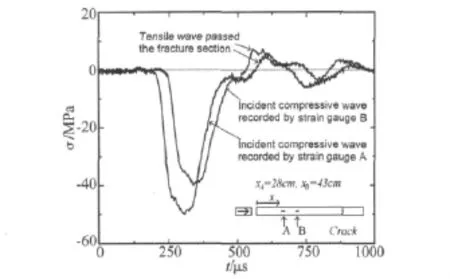
图5 不同位置实测应力波形Fig.5 Signal recorded by the strain gauge

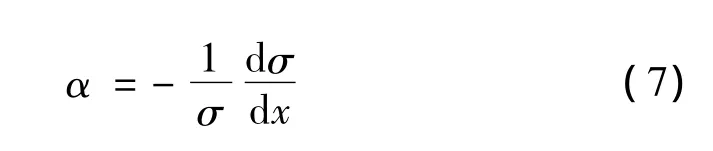
积分式(7)可得应力幅值沿杆长的衰减规律:

其中:σ0为试件入射端的应力幅值;x为与试件入射端距离。文中，我们认为压缩应力波与拉伸应力波具有相同的衰减系数α。

由应变片实测信号可以得到A、B、C三组试件其衰减系数 α 分别为0.721 0/m、0.524 2/m 和 0.473 6/m，进而可以推算出试件入射端的应力幅值σ0。由实际测得的试件中的弹性纵波波速C0可以确定混凝土的弹性模量E(，A、B、C三组试件的弹性模量依次为 31.56 GPa、39.27 GPa 和44.13 GPa。按一维弹性波的理论，我们对试件自由端附近的入射压缩波和反射拉伸波相互作用进行计算，得到不同时刻试件自由端附近的应力分布(图6)，其中，水平轴为距离脉冲入射端的距离，曲线为各时刻自由端附近的应力分布，图中直线近似为不同时刻拉应力峰值点的连线［12]，由实验后测得的层裂位置便可得到该处的最大拉应力为19.50 MPa，层裂发生的时刻为 394 μs。

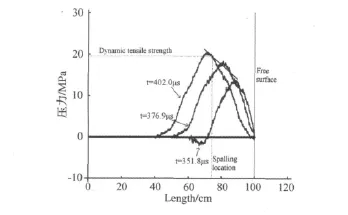
图6 动态抗拉强度确定Fig.6 The determination of dynamic tensile strength

应变率可由层裂位置处的应力得到:

其中:断裂时间t为拉伸应力波产生与层裂发生的时间间隔。

图7为本次实验钢纤维混凝土在不同应变率下的动态抗拉强度(具体数据见表2)，其强度随应变率增加而提高，是一种典型的应变率敏感材料。对于混凝土材料层裂强度的应变率效应，可以采用如下解释:低应变率时，在拉应力作用下，试件内裂纹沿着材料强度最弱的砂浆和砂浆/骨料界面扩展并相互贯通，使得试件破坏，其抗拉性能取决于砂浆和砂浆/骨料界面的强度，与骨料强度关系不大;高应变率时，材料变形过快，砂浆和骨料/砂浆界面中的裂纹来不及扩展，裂纹穿过强度相对较高的骨料扩展，此时，骨料强度对材料的抗拉性能贡献增大，表现出较高的抗拉强度。另外，钢纤维混凝土的动态抗拉强度要明显高于素混凝土，表明了钢纤维对材料抗拉性能的增强和改善作用。通过观察层裂断面，我们发现钢纤维是拔出型而非拉断型破坏。采用环境扫描电镜，我们对拔出钢纤维进行了微观形貌分析，图8为钢纤维微观扫描图像。相比于未使用的钢纤维，拔出的钢纤维表面残留大量水泥胶体，正是这层特殊的粘结层能将作用于混凝土基体上的荷载传递给纤维，两者协同受力。钢纤维混凝土试件层裂破坏时，除砂浆、砂浆/骨料界面和骨料中的裂纹扩展，拔出钢纤维还需克服钢纤维与砂浆粘结的剪滞力，因而需要消耗更多的能量，整体表现为材料动态抗拉强度的提高。

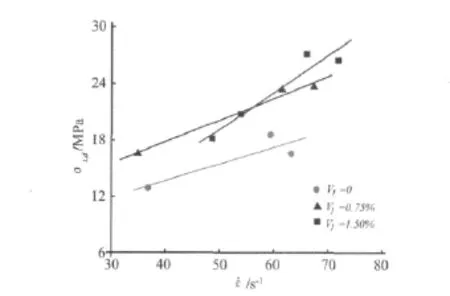
图7 动态抗拉强度应变率效应Fig.7 Strain rate effect of dynamic tensile strength

图8 钢纤维微观扫描图Fig.8 Micro scanning image of steel fiber

为比较不同钢纤维体积材料动态抗拉强度对应变率的敏感性，我们采用动态增强因子(dynamic increase factor，DIF)来表征其应变率效应，定义为动态抗拉强度与准静态抗拉强度的比值，即:

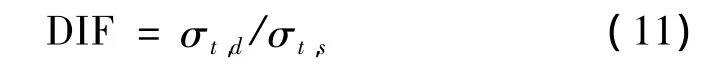
其中:σt，d为动态抗拉强度;σt，s为参考应变率准静态抗拉强度。

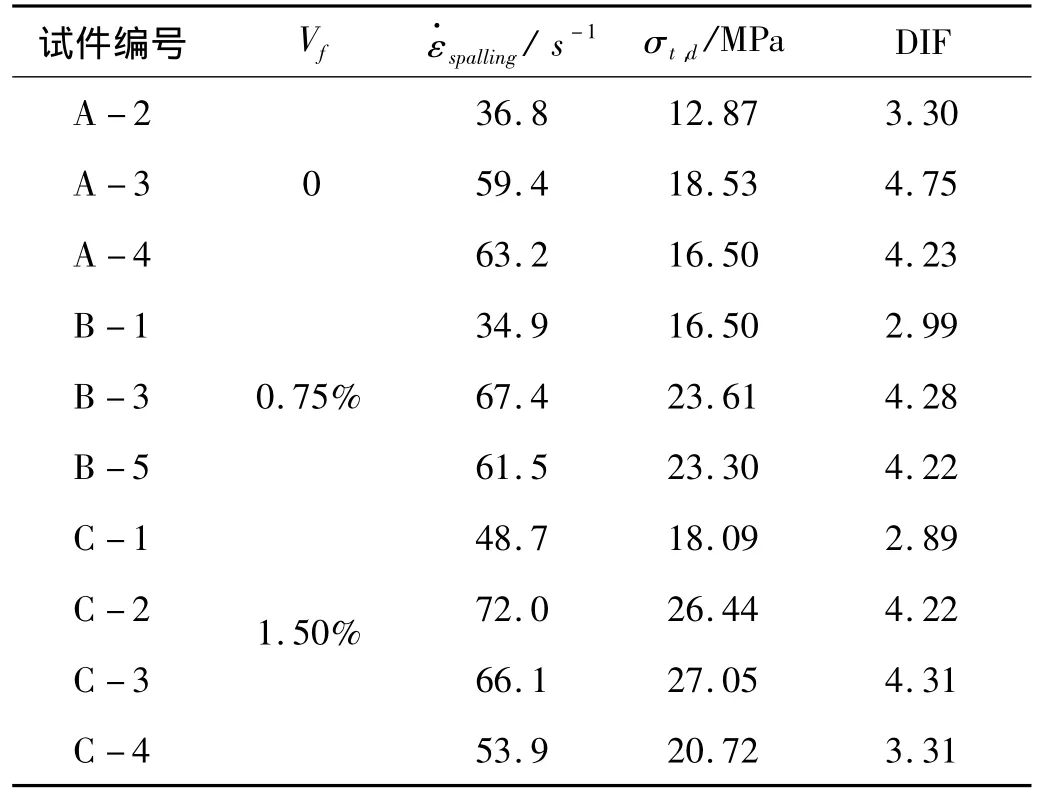
表2 钢纤维混凝土动态抗拉强度Tab.2 Dynamic tensile strength of SFRC

衡量材料的应变率效应就需选定一个参考应变率，此应变率下，DIF=1。美国材料与试验协会(American society for testing and materials，ASTM)建议混凝土准静态抗拉强度的加载率为100 psi/min－200 psi/min(0.7 MPa/min －1.4 MPa/min)，折合平均应变率为2.8×10－7s－1－1.3 ×10－6s－1;欧洲混凝土学会 CEB 将参考应变率取为 3.6 ×10－7s－1－1.7 × 10－6s－1。参照Malvar［16]的建议，我们将准静态应变率取定为 1.0 ×10－6s－1，前文中劈裂实验的应变率选定即基于此。图9为动态增强因子DIF随应变率关系图，可以看出，素混凝土抗拉强度的应变率效应最明显，表现为在相同应变率下其动态增长因子DIF最大，而钢纤维体积率为1.5%的混凝土对应变率最不敏感，这与材料强度越高(一般以立方体抗压强度进行衡量)，其应变率效应越不明显的结论［16]相一致。

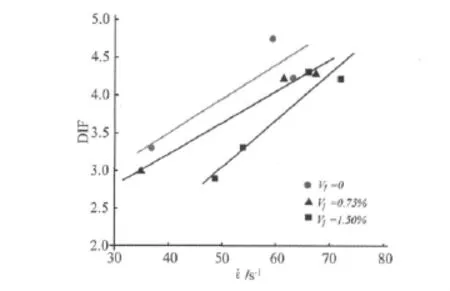
图9 DIF应变率效应Fig.9 Strain rate effect of DIF

3 讨论

基于线弹性力学行为和一维应力波的基本假定，我们采用Φ75 mm大直径SHPB实验系统对钢纤维体积率Vf=0、0.75%和1.50%的三种混凝土材料进行了一维杆状试件的层裂实验研究，通过计算试件表面粘贴应变片所记录的应力信号获得了材料的动态抗拉强度，结果表明钢纤维混凝土动态抗拉强度随着应变率的增加而提高，具有明显的率敏感性，其应变率效应与材料强度有关，表现为材料强度越高，其应变率效应越不明显。本文为测试诸如陶瓷、岩石和混凝土等脆性材料动态抗拉强度提供了一种有效方法。通过对层裂面拔出的钢纤维进行微观扫描，分析了钢纤维改善混凝土抗拉性能的机理。

文中我们并未对压缩应力波引起的材料损伤演化进行考虑，但已有研究表明，对于幅值不高的入射压缩波，试件内部的初始损伤也会发生演化［17]，因而，本文的实验结果具有一定的近似性。另一方面，对于最大拉应力瞬时断裂准则是否适用于钢纤维混凝土材料亦未作进一步的验证，这些都有待后续的实验予以研究。

［1] Metha PK.混凝土结构、特性和材料［M] .上海:同济大学出版社，1988.

［2] Komlos K.Factors affecting the stress-strain relation of concrete in uniaxial tension［J] .ACI J.，1969，66(2):111－114.

［3] Takeda J，Tachikawa H.Deformation and fracture of concrete subjected to dynamic load［C] //Proc.of the Int.Conference on Mech.Behavior of Materials，Concrete and Cement Paste，Glass and Ceramics，Kyoto，Japan，1971，4:267 －277.

［4] Cowell W L.Dynamic propertiers of plain portland cement concrete［D] .Tech.Rep.No.R447，U.S.Naval Civ.Engrg.Lab.，Port Hueneme，Calif.，1966.

［5] Wakabayashi M，Nakamura T，Yoshida N，et al.Dynamic loading effects on the structural performance of concrete and steel materials and beams［C] //Proc. Seventh World Conference on Earthquake Enngrg.，Istanbul，Turkey，1980，6(3):271－278.

［6] John R，Antoun T，Rajendran A M.Effect of strain rate and size on tensile strength of concrete［C] .Proceedings，1991 APSTopical Conference on Shock Compression of Condensed Matter，Williamsburg， VA， Elsevier Science Publishers，1992:501－504.

［7] Mellinger F M，Birkimer D L.Measurement of stress and strain on cylindrical test specimens of rock and concrete under impact loading［R] .Technical Report 4 －46，U.S.Army Corps of Engineers， Ohio River Division Laboratories，Cincinnati，Ohio，April 1966，71.

［8] Birkimer D L.Critical normal fracture strain of portland cement concrete［D] .University of Cincinnati，1968.

［9] McVay M K.Spall damage of concrete structures［D] .U.S，Army Corps of Engineers， Waterways Experiment Station，1988.

［10] Ross C A，Thompson P Y，Tedesco J W.Split-hopkinson pressure-bar tests on concrete and mortar in tension and compression［J] .ACI Materials Journal，1989，86(5):475－481.

［11] Antoun T H.Constitutive/failure model for the static and dynamic behaviors of concrete incorporating effects of damage and anisotropy［D] .The University of Dayton，Dayton，Ohio，1991.

［12] Gálvez D F，Rodríguez P J，Sánchez G V.The spalling of long bars as a reliable method of measuring the dynamic tensile strength of ceramics［J] .International Journal of Impact Engineering 2002，27:161－177

［13] 王礼立.应力波基础［M] .北京:国防工业出版社，2005.

［14] Kolsky H.Stress waves in solids［M] .New York:Dover Publications Inc.，1963.

［15] Johnson W.Impact strength of materials［M] .London:Arnold，1972.

［16] Malvar L J，Crawford J E.Dynamic increase factors for concrete［C] //Twenty-Eighth DDESB Seminar Orlando，FL，1998.

［17] 胡时胜，王道荣.冲击载荷下混凝土材料的动态本构关系［J] .爆炸与冲击，2002，22(3):242－246.