基于独立分量分析与希尔伯特－黄变换的轴承故障特征提取

唐先广， 郭 瑜， 丁彦春

(昆明理工大学 机电工程学院，昆明 650093)

现代滚动轴承故障监测与诊断中多采用多测点、多通道同步采集方式。原始采集信号易受到无关振源所产生振动的干扰，各传感器采集的信号常为多振动源信号相互调制后的混合信号。同时，此类信号大多数为非平稳信号。如何从该类信号中提取出故障特征信息，在滚动轴承故障特征提取中显得尤为重要［1]。

独立分量分析(Independent components analysis，ICA)是随着盲源分离问题(Blind source separation，BSS)的研究而发展起来的一种新方法，其可实现对混合信号中具有统计独立性的信号分量进行有效分离。希尔伯特－黄变换(HHT)是一种自适应信号时频分析方法，其包含经验模式分解(Empirical mode decomposition，EMD)分解和Hilbert边际谱求解过程。对信号进行HHT后可以得到信号能量完整、精确的时频分布，进一步可以得到信号的Hilbert边际谱，实现机械故障的准确诊断［2]。在 HHT的实际应用中，受到采样频率，边界效应，当信号之间的频率比和能量比超出一定值时，易受其他振源高能量的干扰，尤其是与滚动轴承早期故障类似的冲击振源，表现为能量相对比例大的调幅叠加信号。一方面，EMD往往无法分解出正确的本征模式函数(Intrinsic mode function，IMF)［3]，另一方面，Hilbert变换也不能准确分离出具有调幅且能量相对大的信号［4]。在基于HHT的故障特征提取中，无论哪一种情况发生都可能影响对机械故障的准确诊断。本文采用ICA与HHT结合的方法以提高HHT的机械故障特征提取能力。

1 ICA简介

近年来，ICA在机械振动特征提取中按源分离方面得到广泛研究与发展［5－6]。其基本思想可解释为:设计一个逆线性变换矩阵W对N个观测信号X=［x1(t)，x2(t)，…进行变换，并根据源信号独立性原则确定分离准则或目标函数，当选取的逆变换矩阵使目标函数达到最大或最小值时，则变换后可得到相互统计独立的M个源信号S=［s1(t)，s2(t)，…，sM(t)]T，进而实现在源信号S和混合矩阵A都未知的情况下从观察信号分离出相互统计独立的源信号的目的。若 N≥M，则可表示为［7]:

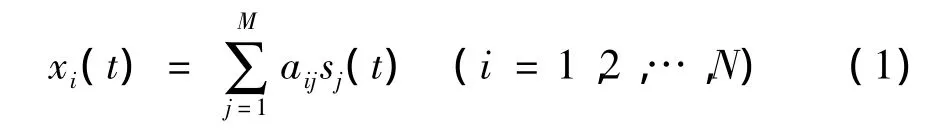
或以矩阵形式简化为:

求解线性混合分离矩阵W使:

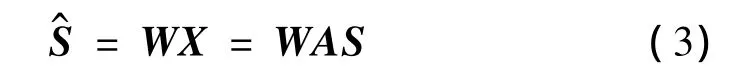
实际应用中，测量数据往往会有过学习和数据中的噪声干扰，ICA中需要对测量数据进行预处理［7]，如时间滤波、去均值、白化等。ICA因分离准则或目标函数的不同，存在多种不同的算法。本文采用基于近似负熵最大化的 FastICA［8]算法。

2 HHT简介

HHT是近年来发展起来的一种信号自适应时频分析方法。其基本思想是通过EMD，将信号分解成一系列近似单频率成分的本征模式函数IMF;对每个本征模式函数进行Hilbert变换，可以得到每个本征模式函数的瞬时频谱，由于经验模式分解是完备的，因此，将各个IMF的瞬时频谱组合起来，就可以得到整个信号的频谱［9]。HHT的首要步骤是对信号进行EMD分解。

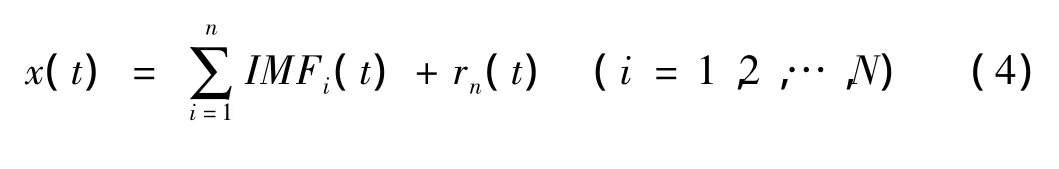
对任意信号x(t)其EMD过程可表示为［9] :式中，分量 IMF1，IMF2，…，IMFn分别为信号频率从高到低的成分，每个IMF必须满足如下两个条件:一是整个信号时间序列中，极值点的个数与过零点个数相同或最多相差一个，二是由极大值和极小值点确定的上下包络线均值为零;rn(t)为余项。不难看出，EMD的本质为信号的分频带滤波［9]，EMD依据不同的频率信号在时间特征尺度上的不同，通过“筛”的过程将任意信号分解成若干的IMF及余项的和。由于滚动轴承振动信号的主要信息在高频段，前几个IMF分量包含了原始信号的主要信息［10]，研究中选取了前3个IMF进行分析已有效的包含滚动轴承的故障信息。Huang曾指出，HHT对于非线性、非平稳信号的分析比其它时频分析方法能更好地反映信号的物理意义。对于任意一个IMFi(t)时间序列，其 Hilbert变换 yi(t)定义［11]如下:

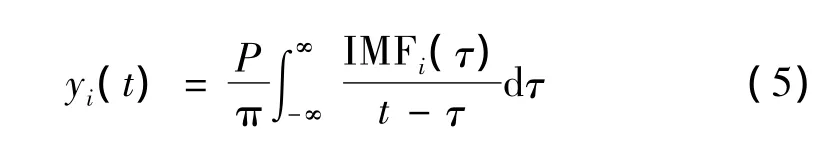
其中P为Cauchy主值，一般可取P=1［11]。信号xi(t)的解析信号zi(t)表示为:

瞬时频率的定义:

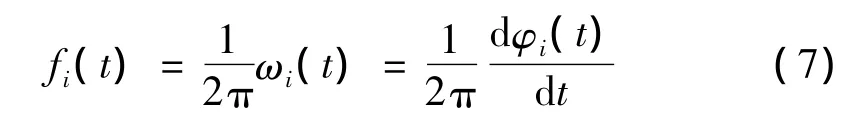
其中:Hilbert变换实际上是信号IMFi(t)和时间t的倒数1/t的卷积，因此，Hilbert变换能够突出信号IMFi(t)局部特征［11]。在应用HHT时存在一个比较突出的问题为所谓的端点效应问题。国内外文献表明可以通过包括基于神经网络的数据延拓、极值点延拓法和基于AR模型的时间序列线性预测方法［9]等可改善端点效应。本文研究中采用在长数据段中的简单的端点数据舍弃法。

3 HHT-ICA方法

图1 基于HHT和ICA对滚动轴承的故障特征提取方法框图Fig.1 Schematic of the faults features extraction on rolling element bearing based on HHT－ICA

其基本步骤为:首先采用EMD方法把采集得到的原始振动信号分解为IMF分量，选取前3阶IMF分量(对应原信号中的高频成分)，再利用带通滤波和Hilbert变换获得信号的包络波形，随后对此包络波形进行ICA分离，得到包络波形中包含的各独立分量，最后通

基于HHT和ICA对滚动轴承的故障特征提取方法框图如图1所示:过FFT分别得到各独立分量的包络谱，从而实现对原混合信号中干扰成分和故障成分的分离，获得对滚动轴承故障的准确诊断信息。值得注意的是，本方法中结合HHT和ICA的各自优点，首先利用HHT中的EMD来实现对原始振动信号的分频带滤波，并选取高频带IMF作为后续的分析对象，从而衰减原始振动信号中低频IMF的影响，而后经共振解调提取的包络信号。由于滚动轴承包络提取使用的共振区频率较高(通常数千赫兹以上)，可有效减少低频干扰(如:偏心、不平衡等引起的振动)的影响，而能到达高频共振区的信号通常为冲击振动和白噪声，对应的独立振源数目有限，更容易满足ICA算法在实际应用要求混合信号观测数目不少于独立源数目(N≥M)的条件(参见本文第1节)。

值得指出的是，近来，文献［3] 提出了一种用ICA消除EMD分解后各IMF之间信息混淆问题，该方法首先采用EMD将原始采集信号分离成若干IMF，再以各IMF分量作为输入采用FastICA进行去除IMF混淆分离，最后选择FastICA中某一输出量进行时频分析，进而实现滚动轴承的故障特征提取。但实际应用中，由于通常源信号数目事先未知且较多，而测点数量有限，不易满足通常ICA算法中要求观测数目不少于独立源数目(N≥M)的条件，因而可能导致不能得到包含主要故障信息的独立分量，而本方法采用包络波形作为ICA输入有效减少了振源数目，因此可弥补文献［3] 中提出方法的不足，更适合于对滚动轴承故障特征的准确提取。

4 仿真试验分析

本文采用对具有较大能量的两脉冲信号源的分离过程，模拟验证ICA在HHT分析中的降噪作用。仿真数据生成公式如下:

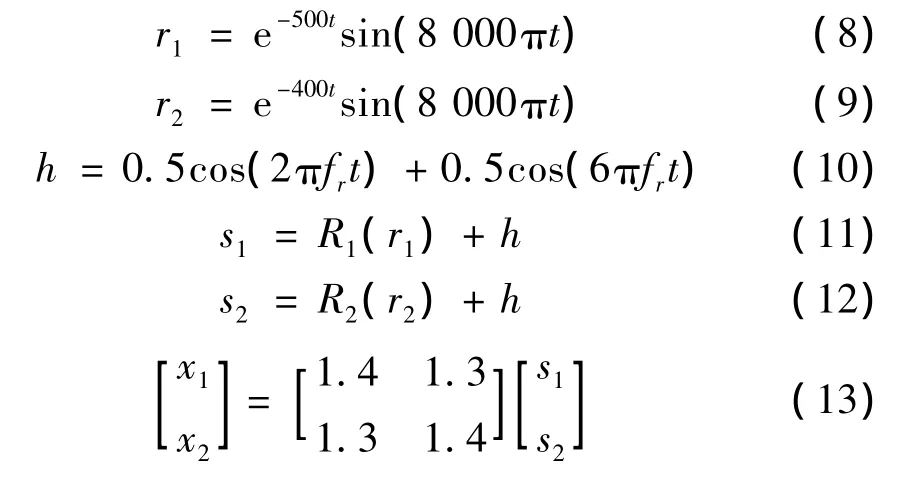
简化为:

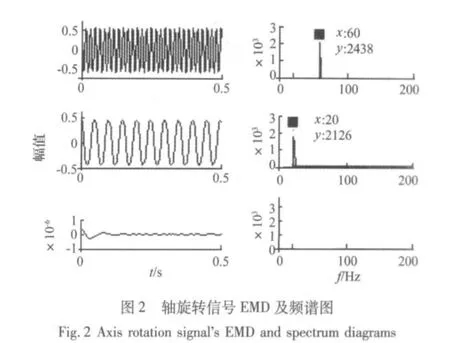
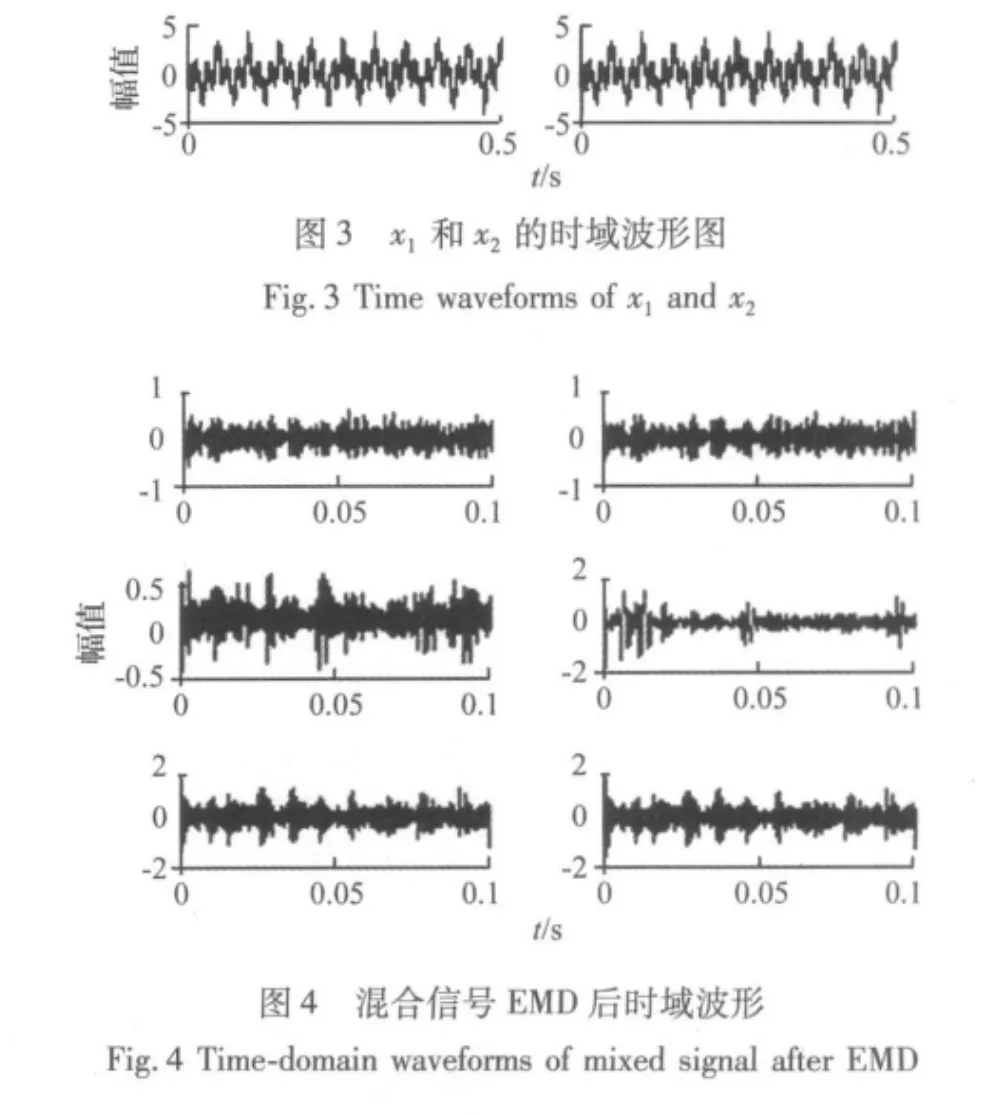
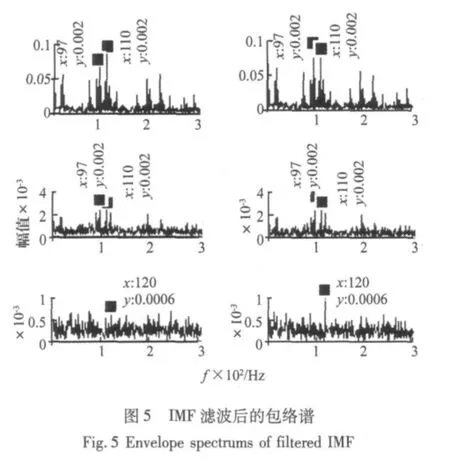
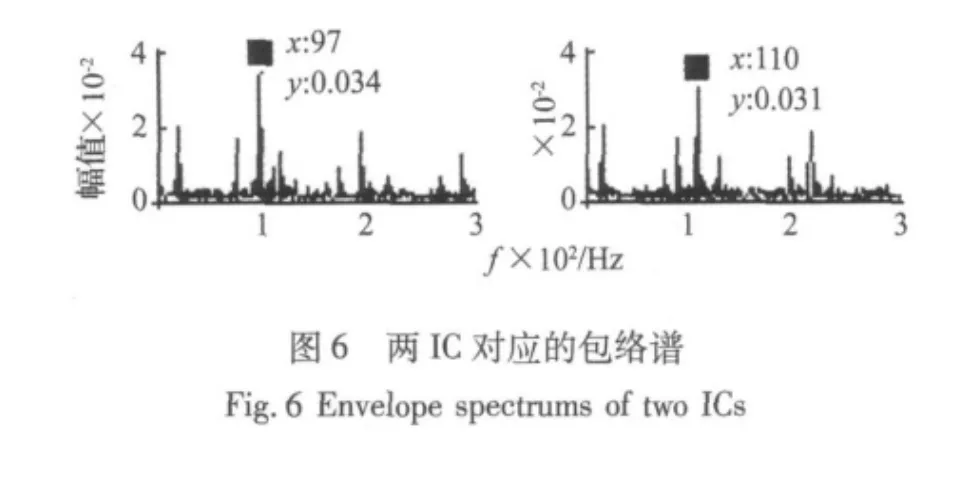
式中，h表示模拟轴旋转频率相关低频振动，其中fr=20 Hz(对应转速1 200 r/min)，经EMD后时域波形图和频谱图(如图2 所示)，表明该信号中低频信号已被EMD准确分离。r1和r2为模拟系统固有频率衰减信号;R1(r1)是以r1为主周期(频率为110 Hz，幅值为1)的周期滚动轴承故障仿真信号;R2(r2)是r2为主周期(频率为97 Hz，幅值为1)的其它振源仿真信号;s1和s2经混合矩阵B后得到混合信号x1和x2(如图3所示)。x1和x2分别经EMD后时域波形如图4所示(每列表示前3个IMF)，再对所有IMF以带通滤波器(带宽为3 500 Hz～4 500 Hz)后经Hilbert得到的包络谱如图5所示，不难看出EMD分离出的IMF包络谱中仍然含有97 Hz、110 Hz等频率及其倍频，这表明传统的HHT方法对多振源混合信号中的冲击干扰并不能实现准确分离。若以EMD的输出信号作为ICA的输入，对混合信号的包络波形进行FastICA分解后得到的其中两个独立分量对应的包络谱如图6所示，从图中可清晰观察到对应于冲击源信号s1和s2的频率成分，这表明本文提出的方法实现了对混合观察信号x1和x2的准确分离。仿真试验结果表明在传统的HHT方法对多振干扰信号分离失效的情况下，ICA可有效克服传统的HHT方法对多源干扰信号的分离能力的局限性，从而实现强干扰下对滚动轴承故障特征信号的有效提取。

5 试验信号分析

为验证本方法的可行性，本文以QPZZ－II型旋转机械振动及故障模拟试验台为测试对象，进行了滚动轴承外圈和内圈故障试验研究，下面以外圈故障试验为例进行论述。试验基本参数为，外圈故障轴承型号:N205，安装轴转速:1 200.16 r/min(对应的转轴回转频率为20 Hz)，数据采集设备:NI PXI－1042Q，3通道采集，采样频率:40 kHz，传感器采用CA－YD－1875TNC加速度传感器，灵敏度:100mV/g，安装位置:轴承座。试验中采用JZ－Ⅰ型激振器产生频率分别为92 Hz、110 Hz、132 Hz的方波对轴承座进行激振作为外部强干扰源，本文以132 Hz方波激振频率实测数据分析为例说明本方法的有效性。采用与仿真数据分析方法相同的分析步骤，对采集数据通过低频截止频率为2 300 Hz，高频截止频率为3 000 Hz的带通滤波后时域波形，如图7所示。

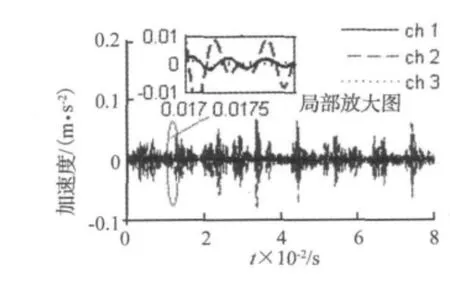
图7 采集信号时域波形图Fig.7 Data acquisition waveforms from 3 channels

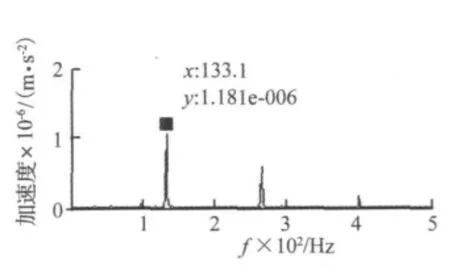
图8 分离出的激振器干扰分量包络谱图Fig.8 Envelope spectrum of the separated IC corresponding to the exciting vibration from vibrator

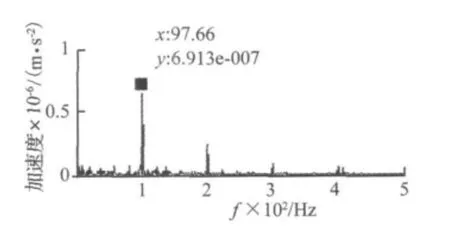
图9 分离出的滚动轴承外圈故障分量包络谱图Fig.9 Envelope spectrum of the separated ICcorresponding to the vibration from the fault of inner race

对3通道采集信号进行EMD分解，得到各IMF波形，以每通道EMD分解的3组IMF由Hilbert提取包络波形后作为输入，再经FastICA运算后的HHT分量输出，频谱分析分别得到含有133.1 Hz及其倍频的包络谱(如图8所示)和含有频率为97.66 Hz及倍频的频谱如图9所示。由前述可知，图8中的133.1 Hz频率及其倍频大约与施加的激振器激振频率一致，故可判定为激振器振动产生。图9中的97.66 Hz及其倍频对应滚动轴承外圈故障理论特征频率(由文献［12] 通过计算可知轴承外圈理论计算一阶径向故障振动频率约为97 Hz)。由此可见，本文方法实现了滚动轴承外圈故障特征在外部强干扰条件下的准确提取。值得指出的是:与仿真试验分析结果一致，上述试验数据用传统的HHT方法也不能实现对上述故障信号和干扰信号进行有效分离，由于篇幅限制，此处不再列出。

6 结论

仿真和实验结果表明，ICA为HHT在故障特征提取和诊断中提供了更为广泛的应用范围。本方法不仅能有效解决直接EMD分解过程中各IMF分量相互混叠而不能准确分离的不足，同时，利用提取的包络波形作为ICA输入可有效减少信号中的振源数目，使后续ICA分离条件更容易在工程应用中得到满足。ICA和HHT技术的结合，对实现强干扰条件下滚动轴承的故障特征提取和诊断具有较好的应用价值。

［1] 黄 仁.机械制造过程的工况监测与故障诊断［M] .西安:西安交通大学出版社，1991.

［2] Huang N E.Shen Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J] .Proceeding of the Royal Society of London Series A－Mathematical Physical and Engineering Sciences，1998，454:903－995.

［3] 陈建国，张志新，郭正刚，等.独立分量分析方法在经验模式分解中的应用［J] .振动与冲击，2009，28(1):109－111，130.

［4] Tang X G，Guo Y，Ding Y C，et al.Application of independent component analysis in rolling element bearing［C] //.Proc of the 2010 MIMT，January 22－24，2010:74－78.

［5] Guo Y，Tan K K.Order－crossing removal in Gabor order tracking by independent component analysis［J] .Journal of Sound and Vibration，2009，325(1 －2，7):471 －488.

［6] Guo Y，Tan K K.High efficient crossing－order decoupling in Vold－Kalman filtering order tracking based on independent component analysis［J] .Mechanical Systems and Signal Processing，2010，24(6):1756－1766.

［7] Hyväerinen A.Independent component analysis［M] .John Wiley ＆ Sons，2001.

［8] Hyväerinen A.Fast and robust fixed－point algorithms for independent component analysis［J] .IEEE Transactions on Neural Networks，1999，10(3):626 －634.

［9] 于德介，程军圣，杨 宇.机械故障诊断的Hilbert－Huang变换方法［M] .北京:科学出版社，2006.

［10] 杨 宇，于德介，程军圣.基于EMD的奇异分解技术在滚动轴承故障诊断中的应用［J] .振动与冲击，2005，24(2):12－16.

［11] 褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法［M] .科学出版社，2009:109－125.

［12] 陈 进.机械设备振动监测与故障诊断［M] .上海:上海交通大学出版社，1997:98－102.