辐板刚度、阻尼及齿面摩擦对齿轮振动特性的影响
古成中,吴新跃,张文群
(1.91663部队,青岛 266012;2.海军工程大学 船舶与动力学院机械工程系,武汉 430033)
齿轮啮合所产生的振动对机械系统的性能、寿命以及环境造成的不利影响,已经引起了广泛关注。国内外专家学者对此作了大量的研究探索,并取得了一些成果[1-4]。齿面摩擦、齿侧间隙、啮合时变刚度等因素使得齿轮系统具有强非线性。在齿轮非线性动力学方面,国内外学者已经进行了大量的研究[5-9]。但这些研究主要集中在齿轮啮合刚度和齿侧间隙方面,鲜有关于齿面摩擦,及齿面摩擦与啮合刚度耦合方面研究。Velex[10]和 Vaishya 等[11]利用油膜理论建立了齿面摩擦模型,分析了各齿轮参数对单自由度系统性能的影响。Singh等[12]将齿面摩擦简化为库伦摩擦,研究了齿面摩擦力的周期特性。但这些模型基本都将啮合轮齿等效为单对轮齿啮合,不能全面反应齿面的实际摩擦情况。
由于薄辐板具有质量轻、缓振效果好等优点,使其广泛应用于航空航天、军工造船等行业。但是辐板厚度的降低必然会增加轮毂和齿圈之间的扭转变形,降低齿轮传递系统的稳定性。辐板刚度设计不合理可能会增加齿轮传动系统的振动,甚至会使齿轮传动系统失稳。在辐板上增加阻尼材料可以降低齿轮振动,增强齿轮传动系统的稳定性,因此对辐板阻尼的研究具有非常重要的理论意义和实用价值。前人的研究主要集中于辐板厚度和布置等对齿轮振动的影响[13-15],很少有关于辐板阻尼的研究。刘海霞和王三民等[16]研究了辐板对齿轮振动特性的影响,但是他们用平均啮合刚度代替轮齿的实际啮合,而且忽略了齿面摩擦力矩的影响,不能有效地呈现辐板阻尼、时变啮合刚度和齿面摩擦力矩之间的非线性耦合关系。
本文综合考虑轮齿时变啮合刚度、齿面摩擦力矩和辐板阻尼等因素,以单对齿轮啮合为例,建立了齿轮传动系统的三维非线性模型。讨论了这种显含时间变量的强非线性微分方程组的数值解的计算方法,结合Runge-Kutta法的原理,通过Simulink完成数值仿真模型的建立,求出了强非线性时变微分方程组的数值解。
1 啮合刚度的时变性
为了保证齿轮传递的平稳性,要求其重合度ε>1,一般取值范围为1~2,这就使得齿轮啮合过程中出现单齿啮合和双齿啮合的交替出现,从而使得齿轮副啮合刚度发生突变。文献中通常用将轮齿啮合刚度简化为矩形波,仅考虑单齿与双齿啮合交替时产生的突变,而忽略了轮齿自身刚度随啮合点的移动而产生的变化。这种处理方法存在较大误差,不能准确的体现齿轮啮合情况。
本文采用 Cai[17]模型的直齿轮进行刚度计算公式。Cai提出的啮合刚度的计算公式所得到的结果与试验结果比较一致,在工业设计范围内具有足够的精度,各符号说明如下:ki(t):第i个啮合齿轮副的啮合刚度(N/μm);ε:重合度;ni:主动齿轮、从动齿轮的转速(r/min),(i=p,g);m:齿轮模数;zi:主动齿轮、从动齿轮的齿数(i=p,g);β0:节圆上的螺旋角(°);b:有效齿宽(mm);tz:啮合周期,tz=60(ni·zi)(s);h:全齿高,h=2.25 m;ωi:齿轮副的啮合角速度,ωi=2πni/60;y1,y2:齿高修正系数。齿轮副啮合刚度函数近似表达式为:
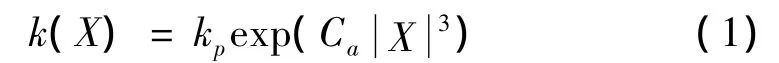
X表示作用线上,从啮入点到啮出点的啮合位置,X的原点位置在啮入点。
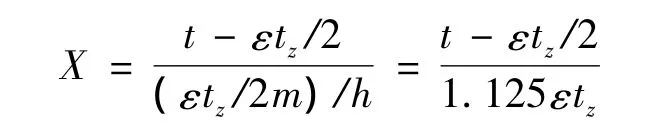
其中:
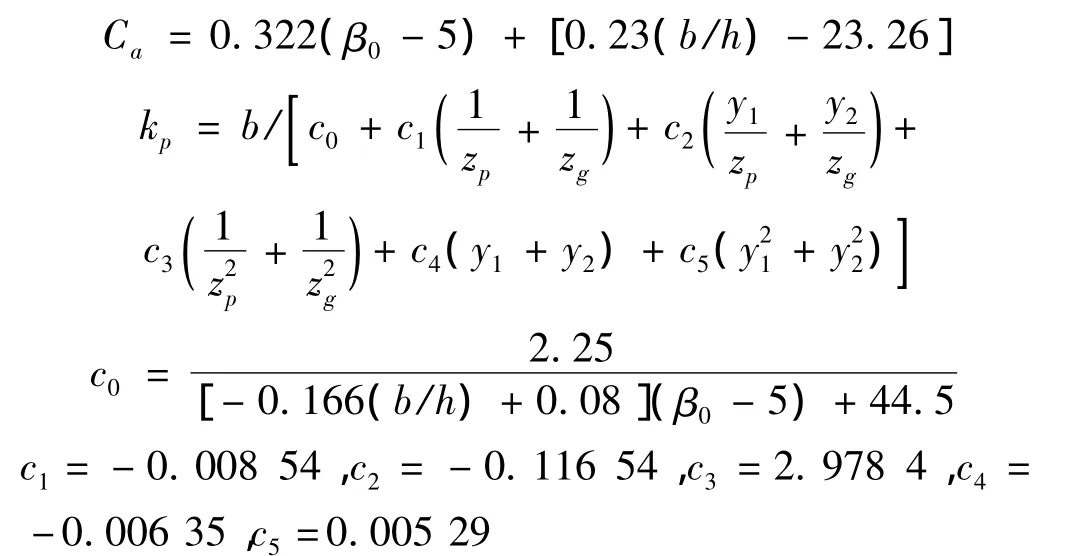
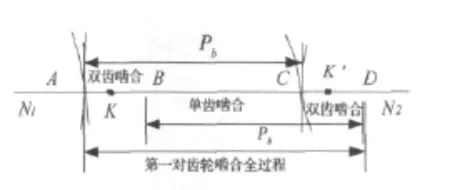
图1 啮合区间示意图Fig.1 Sketch of gear meshing section
设齿轮副在A开始啮入,沿着啮合线N1N2移动至D点啮出,由图1可知AB和CD为双齿啮合区,BC为单齿啮合区,齿轮副整个啮合过程啮合点的移动距离为AD。齿轮啮合周期tz=2π/zpωp,所以啮合点在啮合线上移动一个基节Pb所需时间t2=tz;重合度1<ε<2,由重合度定义知ε=AD/Pb,所以整个齿轮副啮合所需时间 t3=εtz,t1=(ε -1)tz。
将齿轮啮合情况在时间上进行展开,如图2所示,取第一对齿轮副开始啮入的时间t0=0,由啮合周期的定义可以知道,第二对齿轮开始啮合时t2=tz,第三对齿轮开始啮合时t4=2tz,以此类推。
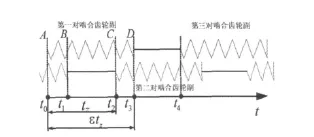
图2 啮合刚度分析Fig.2 Stiffness of gear meshing
可以将齿轮副在时间域分成两组:奇数对齿轮副和偶数对齿轮副。从图2中可以发现这两对齿轮都是以2tz为间隔周期出现,奇数对齿轮副啮合在t0到t3的刚度为k(t),在t3到t4之间没有齿轮副参加啮合,故其啮合刚度为0,所以奇数对齿轮副啮合刚度以2tz为周期的周期函数,可表示为:
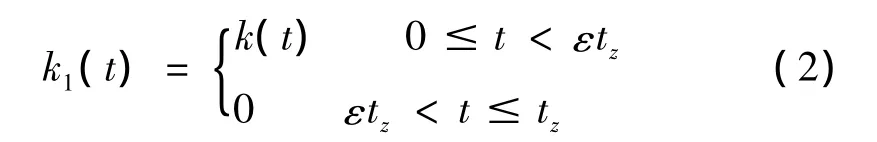
对于偶数对齿轮副,在t0=0是已经有齿轮副正处于啮合状态,该齿轮副已经移动至C点位置,又其周期特性于奇数对齿轮副类似,故其啮合刚度可表示为:
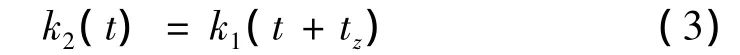
齿轮副啮合刚度数值仿真结果如图3所示,图中k1表示奇数对齿轮副啮合刚度,k2表示偶数对齿轮副啮合刚度,k1+k2为综合啮合刚度。从图中可以发现,如果将齿轮副的时变啮合刚度简化成平均刚度或矩形波,会有较大的误差,影响模型特性分析的真实性。
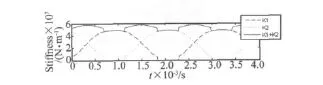
图3 齿轮副啮合刚度Fig.3 Stiffness of gear pair
2 摩擦因素的非线性
齿面摩擦按照润滑状态可分为三类:① 完全弹流润滑状态,即油膜比厚系数λ>3;② 混合润滑状态,1≤λ≤3;③ 边界润滑状态,λ<1。在前人的研究中,针对各种润滑状态都有相应的摩擦系数经验公式,其中以Buckingham半经验公式应用最为广泛[18]。
本文以Buckingham半经验公式为基础,根据齿轮啮合的实际情况对其加以改进,方便了齿轮动力学的求解。Buckingham半经验公式:
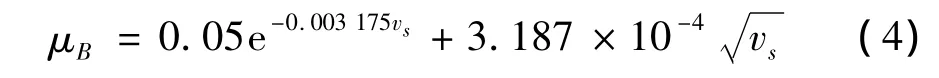
其中vs为轮齿相对滑动速率,可表示为时间t的函数:
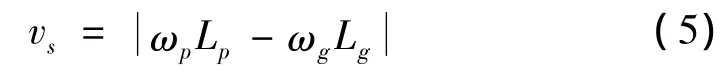
其中Lp、Lg分别为主、从动齿轮齿面渐开线曲率半径:
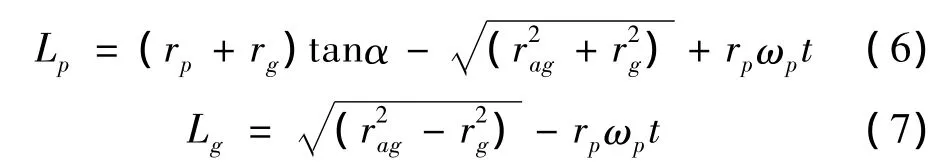

图4 齿轮啮合示意图Fig.4 Sketch of gear meshing
其中参数含义如图4所示。相互啮合的齿面在节圆前后的相对滑动速度相反,而且齿面啮合力也会随着啮合点的移动而变化,所以摩擦力在节圆处会发生方向突变。取奇数对齿轮副开始进入啮合时间为起点,结合式(4)~(7),可以将齿面摩擦系数表示为时间的函数。
另外,齿面摩擦只会在啮合齿面产生,如图4所示,采取和啮合刚度相同的处理方法,将齿轮分成两组,每组摩擦系数都是以2tz为周期的周期函数,改进后的齿面摩擦系数公式为:
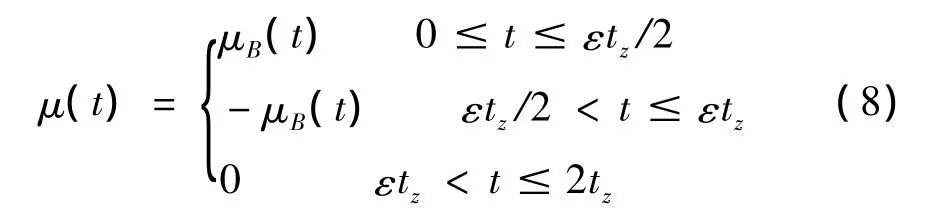
设齿轮副啮合力为Fi(t),则该对齿轮副的齿面摩擦力对主、从动齿轮产生的力矩分别为:
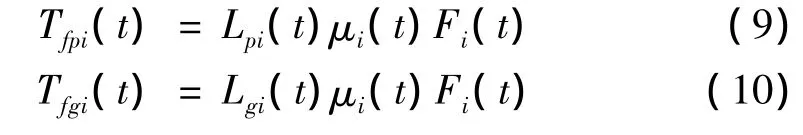
由前面分析可以知道,对于重合度1<ε<2的齿轮而言,其齿面啮合由奇数对和偶数对组成,所以主、从动齿轮所受到的摩擦力矩分别为:
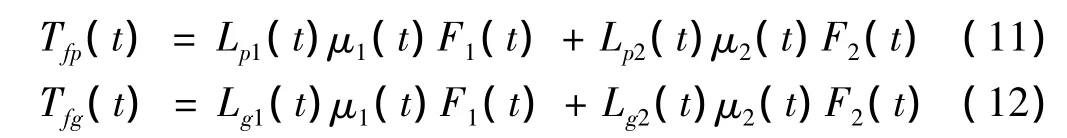
其中力臂 Lp1(t)=Lp(t)、Lg1(t)=Lg(t)、Lp2(t)=Lp(t+tz)、Lg2(t)=Lg(t+tz),摩擦系数 μ1(t)= μ(t)、μ2(t)=μ(t+tz),各齿轮副的啮合力 F1(t)=k(t)s(t)、F2(t)=k(t+tz)s(t),动态传递误差 s(t)=rpθp- rgθg- e(t)。
3 齿轮动力学模型
论文采用集中参数法建立了齿轮系统传动系统扭振动力学模型,具体参数见图5,其中kw为辐板扭转刚度、cw为辐板扭转阻尼系数。由于各啮合齿轮副在同一时刻的啮合刚度不同(见图3),所以载荷在齿轮副之间非均匀分配,而且各齿轮副齿面摩擦力的摩擦力臂不同。轮齿本身的粘性阻尼比齿面摩擦系数小很多,为了更突出齿面摩擦对系统的影响,这里忽略轮齿自身阻尼,根据牛顿第二定律和虎克定律可得到该齿轮传动系统的动力学模型为:
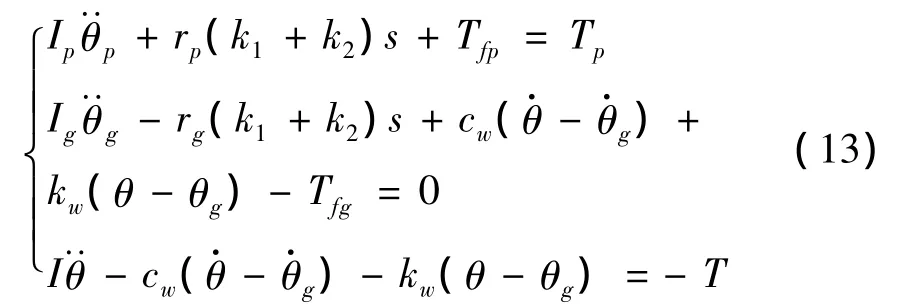
式中 k1、k2、Tfp和 Tfg分别由式(2)、式(3)、式(9)和式(10)求得,动态传递误差 s=rpθp- rgθg-e(t)。为了凸显齿轮系统的振动特性,引入广义坐标:x1=rpθprgθg、x2=θ- θg,代入式(13),消除刚性位移,得到:
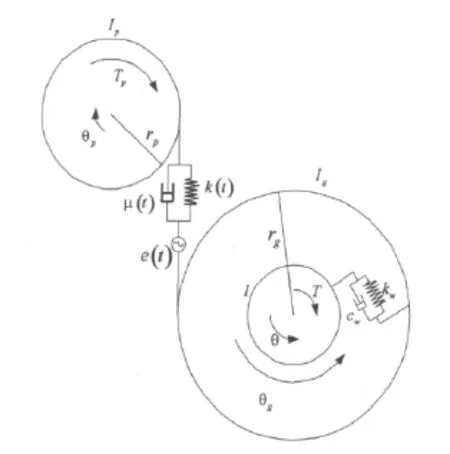
图5 齿轮传动系统动力学模型Fig.5 Dynamic model of gears transmission system

4 齿轮动力学模型的数值仿真
前面所建立的含辐板阻尼、时变啮合刚度和齿面摩擦的齿轮系统非线性动力学模型,从性质上来讲,属于耗散的连续动力系统。对此类系统的数学描述即推导的微分方程,在求解方法上可分为解析法,数值仿真法和模拟仿真法。
齿轮副在啮合过程中,齿面摩擦力的大小和方向都发生周期性的变化,而且与齿侧间隙、辐板阻尼、时变刚度等非线性因素强耦合,使齿轮传动系统表现出复杂的非线性振动特性,一般的解析或半解析分析方法很难得到理想的结果,本文采用数值仿真的方法进行研究。
目前通用软件只能解决常微分方程组问题,对于显含时间t的非线性变微分方程组的解法还很不成熟。论文中采用4~5阶自适应变步长的Runge-Kutta法,通过增加方程组维数的方法将变系数微分方程转化为常系数微分方程组,从而求得该齿轮动力学模型的数值解。
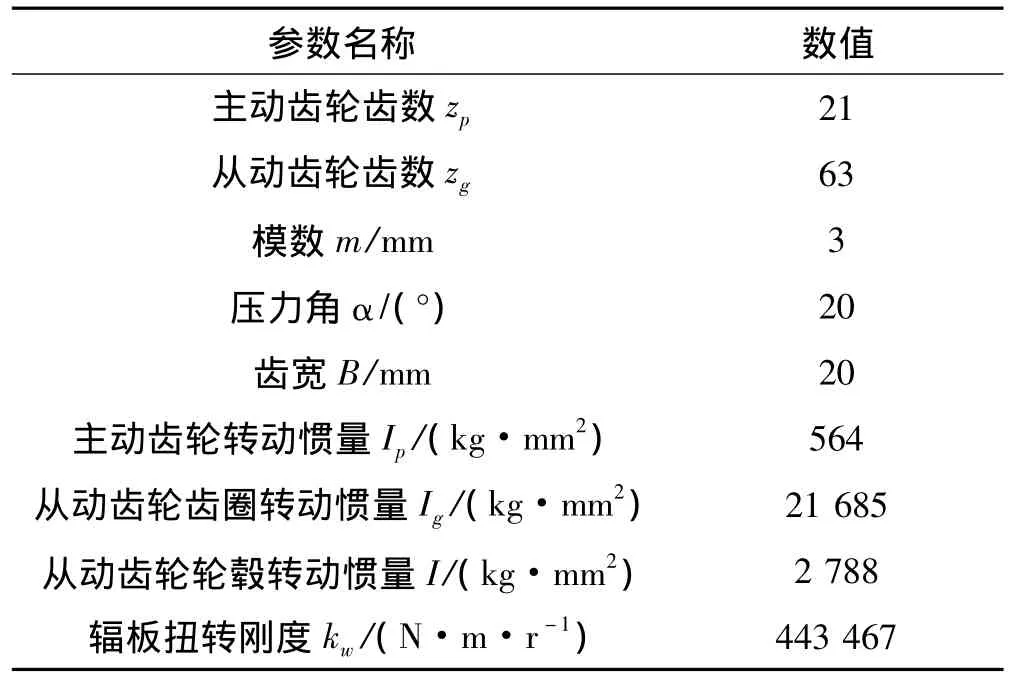
表1 齿轮系统参数Tab.1 Parameters of example gear system
齿轮系统的主要参数如表1所示,其中各质量、转动惯量、刚度是通过UG软件计算求解。
首先研究齿轮辐板阻尼cw对齿轮副振动的影响,如图 6所示,时间单位为 s,综合角位移单位为mm·rad,综合角速度单位为mm·rad/s,下同。在将齿轮辐板视为理想刚体时,其振幅约为0.6 mm;当考虑辐板刚度和阻尼时,在相同载荷激励下,齿轮副振幅降低到0.15 mm。这说明辐板的刚度和阻尼对齿轮副的振动有非常显著的影响,合理的降低辐板刚度对齿轮传动系统的减振效果明显。从相图对比可以看出:忽略齿轮辐板刚度时传动系统近似周期运动,当齿轮辐板有一定刚度时传动系统的运动规律为拟周期运动,在实际的算例中发现随着阻尼的增加,齿轮传动系统运动相轨迹带宽越宽,相轨迹收敛速度越快。这说明辐板阻尼的提高不仅能够降低齿轮副振动,而且还可以增强齿轮传动系统的稳定性。
图7为辐板在不同的齿面摩擦下的振动情况,(a)图中将齿面摩擦系数视为定值ch=0.1,(b)图是按照前面推导的齿面摩擦的非线性公式计算。由图可知(a)、(b)两种情况下,辐板振动的主波形基本相同,频率与齿轮副振动相同;但是考虑齿面摩擦的时变非线性因素时,辐板振动的高阶谐波的振幅明显变大,这说明齿面摩擦的时变非线性特征加剧了齿轮辐板的振动情况。另外,在定摩擦系数的情况下,辐板振动的相轨迹为一定宽度的曲线带,辐板作拟周期运动;在时变非线性摩擦力矩的作用下,辐板振动的相轨迹是以不重复且非闭合的曲线充满相图,此时辐板振动呈现混沌特征,并可能出现分岔现象。
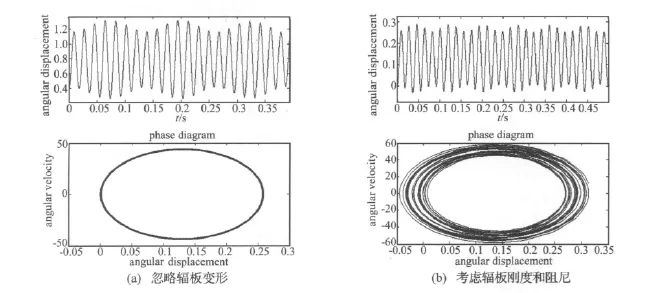
图6 齿轮副振动Fig.6 Gear pair vibration
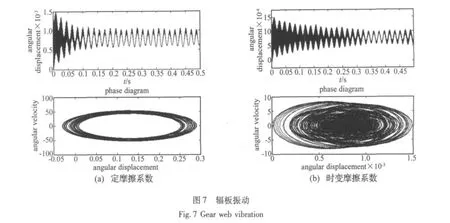
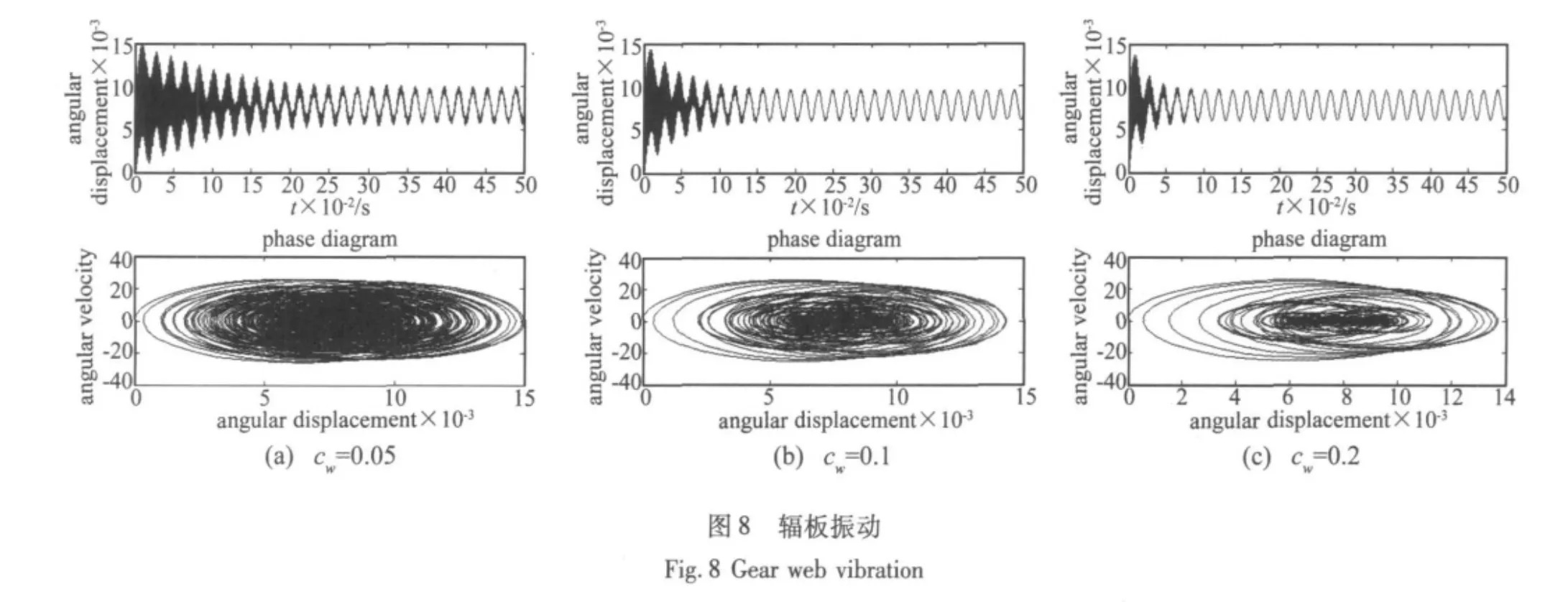
图8为齿轮辐板在各阻尼情况下的振动特性,从图中可以发现辐板阻尼对辐板振动主波形没有影响,但随着阻尼的增加,各高阶谐波被抑制的程度和速度都显著增加;而且从相图看,随着辐板阻尼的增加,其振动相轨迹收敛速度越快。这表明辐板阻尼不仅能够有效地抑制辐板振动,而且还可以提高齿轮传动系统的稳定性。
5 结论
本文建立了考虑齿轮时变啮合刚度、实际齿面摩擦、齿侧间隙非线性及齿轮辐板刚度和阻尼的齿轮系统三自由度强非线性振动模型。该模型的数学形式为显含时间变量的强非线性微分方程组,在模型中考虑了载荷在各轮齿之间的实际分配情况。与前人所建立的模型相比,本模型考虑因素更全面,更符合实际情况,能更准确、全面的体现齿轮传动系统的振动特性。考虑多种非线性因素的耦合能够更接近于齿轮实际的振动情况,但这种强非线性的变微分方程组的求解很困难。本文通过增加方程组维数的方法将变系数微分方程转化为常系数微分方程组,分别利用4~5阶自适应变步长的Runge-Kutta法编程和Simulink的4、5阶定步长法对方程组进行求解,两者得到的结果基本相同,并且与王基等人[19]的研究结论吻合。
通过对齿轮三自由度强非线性振动模型的数值仿真可得到以下几点结论:
(1)通过降低齿轮辐板刚度,可以有效地缓解齿轮副振动。但是随着辐板刚度的降低,齿轮副的运动特性将由周期运动逐渐向拟周期运动转变,甚至会出现混沌现象,影响齿轮传动系统的工作稳定性。
(2)通过增加辐板阻尼的方法,可以显著地提高齿轮副相轨迹的收敛速度,增强系统的稳定性,可以弥补由于辐板刚度降低而引起的不稳定因素。所以综合设计齿轮辐板刚度和阻尼,可以有效地降低齿轮副的振动,该研究具有广泛的应用前景。
(3)时变齿面摩擦因素的引入,增加了齿轮系统的激励,并且产生了复杂的非线性耦合。这使得辐板振动的高阶谐波的幅值明显增加,并且产生了混沌现象,甚至会出现分岔。因此,现在迫切需要加强对齿面摩擦的研究,这对提高齿轮传动系统工作可靠性、降低系统振动有着至关重要的作用。
(4)辐板阻尼主要抑制辐板振动的高阶谐波,随着阻尼的增加其对辐板高阶谐波的抑制效果越明显;并且随着阻尼的增加,辐板振动相图轨迹收敛速度越快,系统稳定性越好。
[1] Andersson A.An analytical study of the effect of the contact ratio on the spur gear dynamic response[J] .ASME Journal of Mechanical Design,2000,122(12):509-514.
[2] Choi ST,Mau SY.Dynamic analysis of geared rotor-bearing systems by the transfer matrix method[J] .ASME Journal of Mechanical Design,2001,123(12):562-568.
[3] Parker R G,Agashe V,Vijayakar SM.Dynamic response of a planetary gear system using a finite element contact mechanics model[J] .ASME Journal of Mechanical Design,2001,122(9):304-310.
[4] Wang J,Howard I.Finite element analysis of high contact ratio spur gears in mesh[J] .ASME Journal of Tribology,2005,127(7):469-483.
[5] Ohue Y,Yoshida A.New evaluation method on gear dynamics using continuous and discrete wavelet transforms[J] .ASME Journal of Vibration and Acoustics,2003,125(7):274-281.
[6] Lin J,Parker R G.Mesh stiffness variation instabilities in two-stage gear systems[J] .ASME Journal of Vibration and Acoustics,2002,124(1):68-76.
[7] He S,Rook T,Singh R.Construction of semi analytical solutions to spur gear dynamics given periodic mesh stiffness and sliding friction functions[J] .ASME Journal of Mechanical Design,DET2008/PTG -122601,130(12):1 -9.
[8] 陆 波,朱才朝,宋朝省,等.大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J] .振动与冲击,2009,28(4):76-80.
[9] 郭 磊,郝志勇,蔡 军,等.汽车变速箱齿轮传动系动力学振动特性的研究[J] .振动与冲击,2010,29(1):103-107.
[10] Velex P, Cahouet V. Experimental and numerical investigations on the influence of tooth friction in spur and helical gear dynamics[C] .Proceedings of the 2000 ASME Design Engineering Technical Conferences,DETC2000/PTG-14430:1-10.
[11] Vaishya M,Houser R.Modeling and analysis of sliding friction in gear dynamics[C] .Proceedings of the 2000 ASME Design Engineering Technical Conferences,Baltimore,USA,2000:601-610.
[12] Blankenship G W,Singh R.A comparative study of selected gear mesh force interface dynamic models[C] .Proceedings of the 6th ASME International Power Transmission and Gearing Conference,USA,1992.
[13] Marunic G.Rim stress analysis of thin-rimmed gear[J] .Key Engineering M materials,Advances in Fracture and Damage MechanicsVI,2007:141 -144.
[14] Al-shyyab A,Kahraman A.Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method:period-one motions[J] .Journal of Sound and Vibration,2005,279:417-451.
[15] Ambarisha V K, Parker R G. Nonlinear dynamics of planetary gears using analytical and finite element models[J] .Journal of Sound and Vibration,2007,302:577 -595.
[16] 刘海霞,王三民,范叶森,等.辐板阻尼对齿轮传动的非线性动力学特性影响研究[J] .机械科学与技术,2009,28(7):965-970.
[17] Cai Y.Simulation on the rotational vibration of helical gears in consideration of the tooth separation phenomenon(A new stiffness function of helical involutes tooth pair)[J] .ASME Journal of Mechanical Design,1995,117(9):460-468.
[18] Buckingham.Analytical mechanics of gears[M] .New York:Dover,1949.
[19] 王 基.引入摩擦和间隙的齿轮传动系统非线性动力学研究[D] .武汉:海军工程大学,2006.

