基于小扰动方程的直升机前飞LQR控制律设计与仿真

谌 昱，杨小龙，王先炜

(中国直升机设计研究所，江西景德镇 333001)

0 引言

以线性二次型调节器为基础的最优控制是20世纪50年代末发展起来的设计控制系统方法。这种方法具有计算简单、便于调整等优点，且得到的最优控制律是状态变量的线性函数，可以利用反馈方法构成闭环控制，在工程上易于实现，已经成为当今控制领域较为主要的设计方法之一［1］。

本文以小扰动方程下的某型直升机模型为被控对象，采用输出反馈LQR技术设计了该型直升机的前飞控制律，并以计入了直升机各执行器后的模型和前飞控制器构成全数字闭环仿真系统进行仿真。结果表明，所设计的前飞控制律控制效果良好，满足性能指标要求。

1 问题描述

1.1 直升机小扰动模型及前飞控制性能指标

直升机状态方程如下:

在小扰动状态下，可建立直升机基于非线性模型的小偏差线性化模型，其状态空间表达式如下［2］:

式中，ΔX∈R9为系统状态变量，Δδ∈R4为控制输入，Y表示输出量。其中，Δu，Δv，Δw分别表示直升机沿机体x，y，z轴的线速度变化量;Δθ，Δφ，Δψ分别表示直升机俯仰角、滚转角和偏航角变化量分别表示直升机俯仰角速度、滚转角速度和偏航角速度变化量。Δδe，Δδa，Δδr，Δδc分别表示旋翼纵向周期变距、横向周期变距、尾桨桨距以及旋翼总距变化量。

由于直升机工作的不稳定性，纵向通道、侧向通道、航向通道以及总距通道之间存在耦合。而在小扰动状态下，为了方便工程设计与分析，忽略纵侧通道之间的耦合作用，将式(2)状态方程分解为纵向状态方程和侧向状态方程。

纵向状态方程如下:

侧向状态方程如下:

系统在获得数据分片后，对分片进行哈希计算，得到每个分片的哈希值后，与之前原数据存储在智能合约中的哈希值进行比对、验证。如果哈希值相同，则系统返回数据未被改动；反之，则提醒用户数据已经被篡改。另外，考虑到分布式存储的容错性，如果出现部分分片丢失，只要丢失的分片数量小于系统数据冗余分片数量，系统仍然能够还原数据源文件，具体如图8所示。

在式(4)和式(5)中，各符号的定义同式(2)。

该型直升机的前飞控制律稳态性能指标是:在设定的单位阶跃激励下，直升机沿机体x轴线速度变化|Δu|≤1 m/s，稳定时间3s到5s，无超调。其他参数 Δv，Δw，Δθ，Δφ，Δψ 也要求变化不大和有较快的稳定时间。

1.2 LQR最优控制器原理

系统(1)二次型目标函数如下:

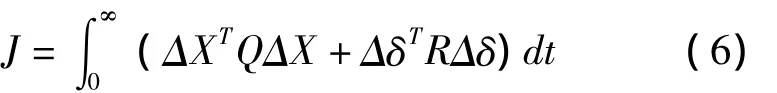
式中，Q，R称为加权矩阵，且Q为9×9维半正定矩阵，R为4×4维正定对称矩阵。最优控制就是寻求控制作用Δδ，如图1所示，使目标函数(6)最小。应用极小值原理，可以求出最优控制作用为Δδ=KΔX=-R-1BTPΔX。其中，P为代数Riccati方程ATP+PA-PBR-1BTP+Q=0 的正半定解［1］。特别的，由于系统(2)的9个状态变量也是系统的输出量，所以状态反馈和输出反馈是等价的。

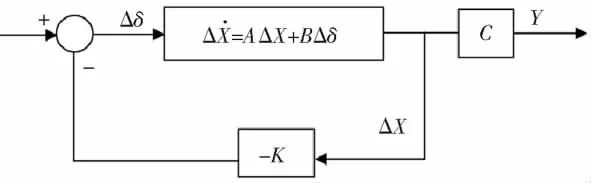
图1 最优控制结构图

因此求解系统(2)线性二次型最优控制律的步骤为:先确定加权阵Q和R，然后求解Riccati方程半正定解P，如果该解P是存在的，即可得到最优控制律Δδ=-KΔX。MATLAB控制系统工具箱中提供了解决线性二次型最优控制问题的命令。其中lqr命令能一次性解出Riccati方程半正定解P和反馈增益矩阵K，命令lqr调用格式如下:

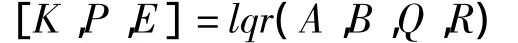
式中，K，P，A，B，Q，R 意义同上，E 为A-BK 的特征值。

1.3 Q，R 的选择原则［3］

Q，R的选择无一般规律可循，一般取决于设计者的经验，常用试行错误法，即选择不同的Q，R代入计算比较结果而确定，这是LQR设计方法的不足之处。这里仅提供几个选择的一般原则:

1)Q，R都是对称矩阵，Q为半正定矩阵，R为正定矩阵。

2)通常选用Q，R为对角线矩阵，实际应用中，通常将R值固定，然后改变Q的数值，反馈增益矩阵在经过仿真后比较确定。

3)Q的选择不唯一。这表明当得到的控制器相同时，可以有多种Q值的选择，其中总有一个对角线形式的Q。

2 前飞控制律设计方案

本节采用输出反馈LQR方法设计该型直升机的前飞控制律。首先需要说明的是，本文使用的直升机小扰动模型是考虑了直升机各个执行通道后的模型。其次，为了调试方便，本文对纵向前飞控制律和侧向前飞控制律分别进行了设计。最后进行全面小扰动状态方程的全数字闭环仿真验证(图2)。在纵向前飞控制律设计中，最优控制律设计中的A，B，Q，R，K 依次对应于 Alon，Blon，Qlon，Rlon，Klon;在侧向前飞控制律设计中，最优控制律设计中的A，B，Q，R，K 依次对应于 Alat，Blat，Qlat，Rlat，Klat。各符号定义在第一节中已有说明。

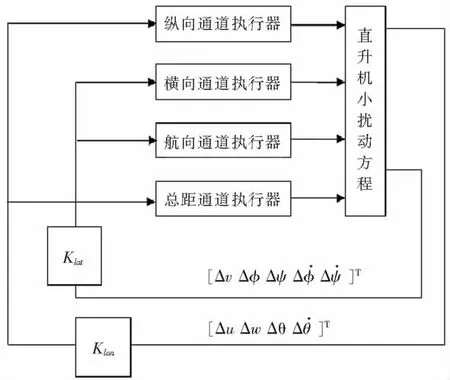
图2 全数字闭环仿真系统结构图

仿真中，适当调整加权矩阵 Qlon和 Rlon，Qlat和Rlat，以得到合适的反馈增益矩阵Klon和Klat，保证前飞控制性能良好。

3 前飞控制律数字仿真验证

首先，选取该4吨型直升机在低高度、前飞速度22m/s、前进比μ=0.1状态下的状态矩阵A、控制矩阵B和单位阵C，建立小扰动模型。然后，利用MATLAB命令设计调试直升机纵向和侧向前飞控制律，并得到全数字闭环仿真系统(图2)。最后，分析直升机在阶跃信号激励后的响应。图3为直升机沿x轴线速度变化量，图4为沿y轴线速度变化量，图5为沿z轴线速度变化量，图6为俯仰角θ变化量，图7为滚转角φ变化量，图8为偏航角ψ变化量的响应曲线。

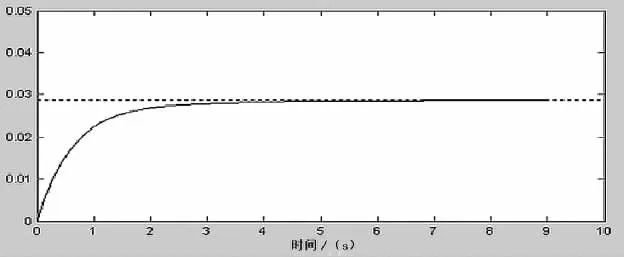
图3 沿x轴线速度变化量

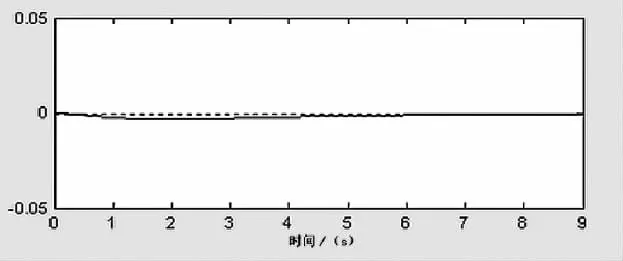
图4 沿y轴线速度变化量

图5 沿z轴线速度变化量

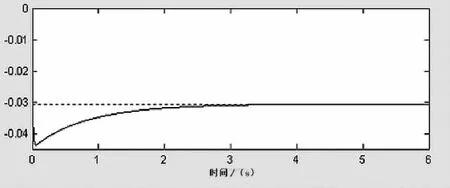
图6 俯仰角θ变化量

图7 滚转角φ变化量

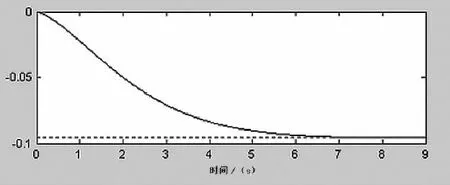
图8 偏航角ψ变化量

从图3可以看出，直升机沿机体x轴线速度变化Δu稳态值不超过0.03m/s(Δu＜1m/s)，无超调，且在靠近5s时就趋于稳定。直升机沿机体y轴线速度基本无变化，Δv≈0，见图4。直升机沿机体z轴线速度有一个很小的下垂量后很快地稳定，稳态值对z轴线速度影响也很小，见图5。从图6、图7、图8可以看出，直升机的俯仰角、滚转角、偏航角的调整过程也是比较理想的，在调整过程中，俯仰角、滚转角、偏航角的最大偏移量依次为 -0.047rad、-0.023rad、-0.09rad，都比较小，而且稳定时间都在7s之内。

综上所述，本文设计的LQR前飞控制律满足提出的稳态性能指标，而且能够保证机体y轴线速度、机体z轴线速度、俯仰角、滚转角、偏航角调整后基本保持不变，控制效果良好。

4 结束语

本文基于直升机的小扰动方程，利用线性二次型最优控制器设计方法设计了某型直升机前飞控制律。以该直升机模型和设计的前飞控制器构成全数字闭环仿真系统进行仿真验证。结果表明，该前飞控制律达到了前飞控制稳态性能指标，而且能够保证其他参数基本不变，控制效果良好。同时，由于是基于状态反馈设计的前飞控制律，容易实现工程应用。

［1］金国龙，王娟.线性二次型最优控制器的MATLAB实现［J］.青岛职业技术学院学报，2004，17(1):36-37.

［2］王庢玉.直升机飞行控制系统［M］.北京:蓝天出版社，1990.

［3］薛定宇.控制系统计算机辅助设计［M］.北京:清华大学出版社，1999.