基于红外热像仪测温原理的物体表面发射率计算

吴燕燕，罗铁苟，黄 杰，郭 芳

(中国直升机设计研究所，江西景德镇 333001)

0 引言

红外热像仪是一种将高于绝对零度物体辐射的不可见表面热转换为可视图像，进而生成热像图和温度值的设备，不仅能获得被测物体表面热场分布的清晰图像，而且还可得出精确的温度测量值。红外热像仪温度测量的准确性受被测表面的发射率、环境温度、大气温度、大气衰减率、太阳辐射等的影响，其中发射率的影响最为突出。物质表面的发射率不仅取决于物质的内在性质，同时还取决于物质表面的物理状态、光滑程度等，这些因素使得发射率的测量很复杂，所以如何确定被测表面的发射率已成为红外热像测温技术中的一个主要课题。

根据不同的测量原理，通常将发射率测量方法分为量热法、反射计法、辐射能量法和多波长测量法等，但每种测量方法各有自己的优缺点，测量的对象也不一样，如量热法中的瞬态量热法只能测量导体材料，稳态量热法只能测量全波长半球发射率，不能测量光谱或定向发射率;反射计法中的热腔反射计法不适用于高温测量，激光偏振法只能测量光滑表面的材料发射率。虽然确定发射率有多种方法，但在实际应用中实现方法比较复杂或费用高。本文从红外热像接收的有效辐射着手，获得两种计算发射率的方法。

1 红外热像仪测温原理

热像仪是靠接收被测物体表面的辐射来确定被测物体的温度。根据红外热像仪的测温原理可知，实际测量时，热像仪接收到的有效辐射包括三部分:目标自身辐射、环境反射辐射和大气辐射，如图1所示。热像仪通常工作在2～5μm或8～13μm两个波段，探测器在工作波段上积分入射的辐射能，并把它转化为一个与能量成正比的电信号。热像仪测温的通用基本公式为［2］:

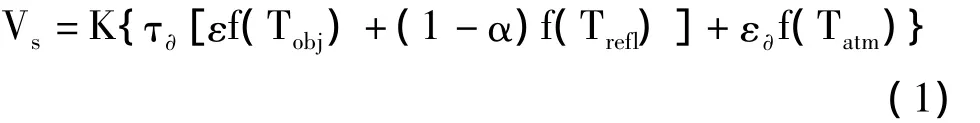
式中:Vs为电压信号，K为常数，τ∂为大气透射率，ε∂为大气发射率 ε∂=1-τ∂，ε为物体表面发射率，α为物体表面吸收率，Tobj为物体表面温度，Tatm为大气温度，Trefl为反射环境温度。

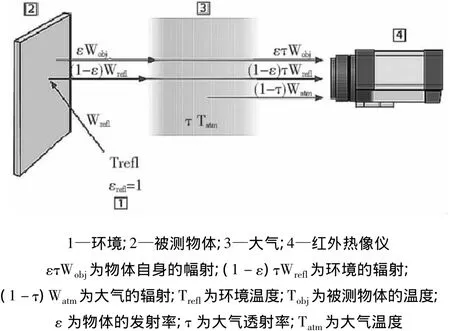
图1 热像仪测量物体温度时接收的有效辐射示意图

根据普朗克辐射定律，将公式(1)进行推导变换，可获得公式(2)［2］:

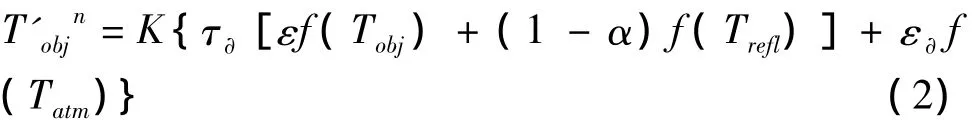
公式(2)进行变化可得公式(3):

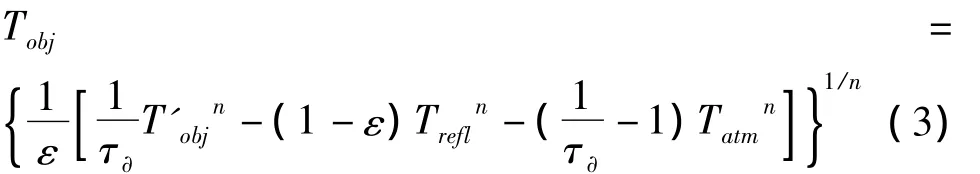
公式(3)为计算灰体表面真实温度的计算公式，当近距离测量或室内测量时，τ∂=1。公式(2)、(3)中的T'obj为热像仪测量物体温度。

当使用不同波段热像仪时，n的取值是不同的，这一点尤其要注意，其中在2～5μm时，n=9.2554，在8 ～13μm 时，n=3.9889。

2 物体表面发射率的计算

各种物质表面的发射率(也称辐射率、黑度系数等)是表征物质表面辐射能力的物理量，是一项重要的热物性参数。用红外热像仪进行测温时被测物体的发射率必须设置准确，否则测出的温度值误差较大，最高可达19%。在短波测量时发射率设定不准所造成的误差比长波测量时的误差要小，如当发射率误差为10%时，0.9μm工作波长的热像仪的测量误差为2%，而8～14μm工作波长的热像仪将形成7% 的测量误差［1］。可见发射率的设置是否准确直接影响测量结果。以下两种方法是从红外热像接收的有效辐射着手获得发射率，简单实用，其测量发射率装置如图2所示。

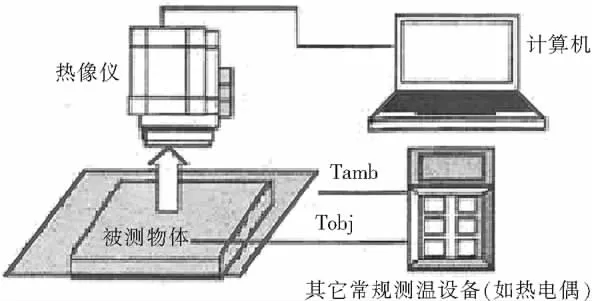
图2 测量发射率装置示意图

由计算灰体表面真实温度的计算公式可得公式(4):

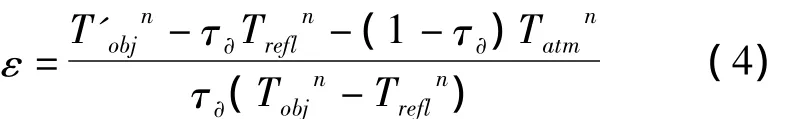
由式(4)可以看出ε与大气透射率、环境温度、大气温度、物体的真实温度、热像仪测量的温度有关。在红外成像时，大气透射率计算的精度会影响红外成像的可信度。大气透射率可通过多种方式获得，如分子吸收的波带模型法、lowtran法、表格法等。当前国内外在对红外成像中的大气透射率进行计算时，大多采用仿真程序调用lowtran并根据实测数据线性拟合透射率计算机公式。

公式(4)中T'obj的测量方法不同，决定了ε的计算方法不同。测量T'obj的有两种方法:

1)将热像仪的ε设置不同的值，对T'obj进行多次测量(三次以上)。

将式(4)进行变换可得:

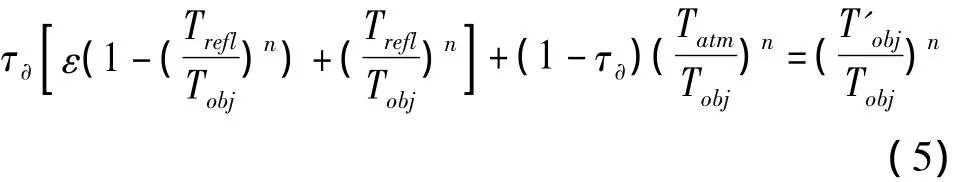
令y=f(ε)，对公式(5)进行变换拟合，可得:

通过红外热像仪测量的数据计算出a和b，由于实际计算出的a值很小，ax小于0.01且比y小一个数量级，所以可忽略不计，由此可得出发射率的计算公式:

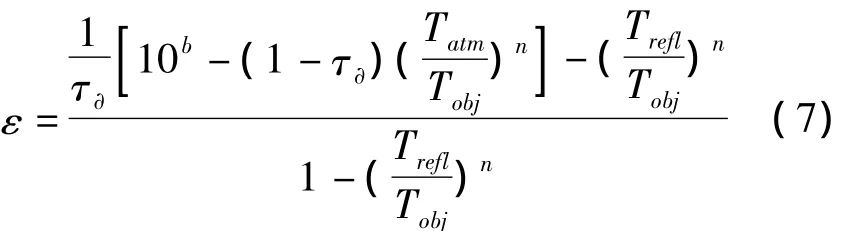
实验方法和步骤:

① Tobj、Trefl、Tatm可利用常用的测温装置测量得到，温度测量精度0.01℃;

②依实际测试环境参数，利用Lowtran7.0计算得到大气透射率;

③将热像仪的发射率ε设为多个不同值(不少于3个)，测出对应的T'obj;

④ 利用 Matlab 将测得的 T'obj、Tobj、Trefl、Tatm数据进行曲线拟合，得出a、b;

⑤将b代入式(7)可得出物体的发射率。

此方法对液体、固体、气体发射率的测量计算均适用。由于对T'obj进行多次测量，减小了测量误差。对测量数据T'obj、ε进行曲线拟合的计算量比较大，工程应用中可采用Matlab进行曲线拟合，得出a、b。

2)将热像仪的ε设置为1，对T'obj只进行一次测量。

若将热像仪的ε设置为1，则公式(2)进行变换可得公式(8):

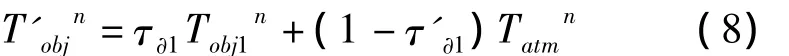
将公式经过变换为公式(9)，此式即为计算发射率的公式。

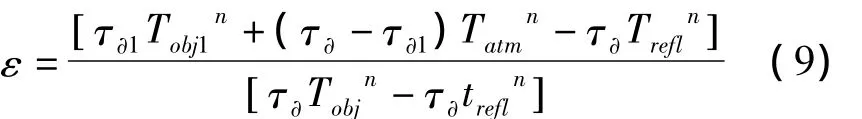
方法二的实验方法和步骤与方法一的相同，只是将ε设置为1，此方法适用于固体和液体发射率的测量，对Tobj、Trefl，Tatm的准确性要求很高。为了测量结果的准确性，要求目标温度与环境温度有一定的温差。

根据以上公式，利用VC编写计算发射率的计算程序，程序界面见图3。

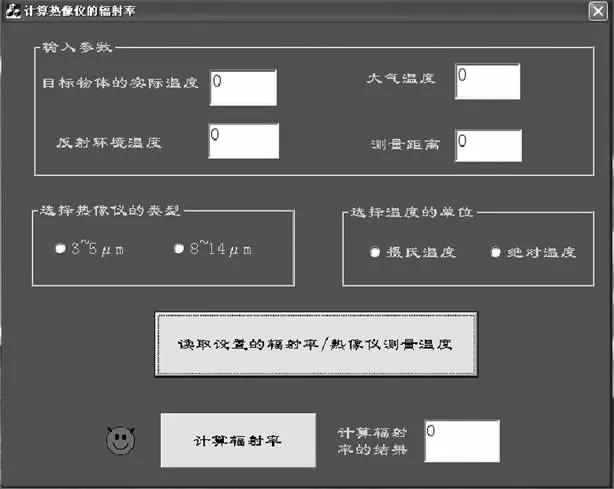
图3 计算程序界面

3 实验过程及结果分析

3.1 实验过程

1)利用方法一进行实验

本项实验在室内进行，设置热像仪的ε=1，对T'obj进行一次测量。实验对象为皮肤、水、纸(深蓝色)、白纸、沙子(潮湿)，实验过程中采用Therma-CAM S65型热像仪，光谱范围为(7.5～13μm);热电偶或热电阻测量目标物体的温度和环境温度，认为环境温度即为大气温度，其温度值为20℃。

2)利用方法二进行实验本项实验均在室内进行，将热像仪的ε设置不同的值，对T'obj进行多次测量(三次以上)。

实验一的测量对象是液压散热器风扇的出口温度，即风扇出口空气温度。实验过程中采用ThermaCAM S65型热像仪;热电偶或热电阻测量目标物体的温度和环境温度，认为环境温度即为大气温度。

实验二的测量对象是空调出口温度。实验过程中采用两种类型的热像仪:ThermaCAM S65型热像仪，光谱范围为(7.5 ～13μm)，ThermaCAM S550 型热像仪，光谱范围为(3～5μm);温度计测量目标物体的温度和环境温度，认为环境温度即为大气温度。以上两项实验均在室内进行。

以上实验的步骤见第2节，实验环境的湿度为65%，测量距离1.5m。

3.2 结果分析

方法一:适合固体和液体发射率的测量，不适合气体发射率的测量，测量参数少，测量方法简单，而且参数测量的精度要求高，所以此方法容易扩大误差。由于是在室内进行测量，被测对象的实际发射率与ε=1相差不大，所以当设置ε=1时热像仪测量的温度与实际温度相差不是很大。从表1可知计算的发射率与参考发射率基本相等。

方法二:适合于固体、液体和气体发射率的测量，测量参数比方法一多，测量方法简单，对参数测量的精度要求不是很高，从表2或表3可知，由于设置了不同的发射率，这样容易消除系统误差。此方法中曲线拟合的计算量比较大。

从结果数据看出，环境温度与目标温度相差较小时，误差明显增大，方法二测量温度的误差小于方法一测量温度的误差，具体热像图见图4、图5。

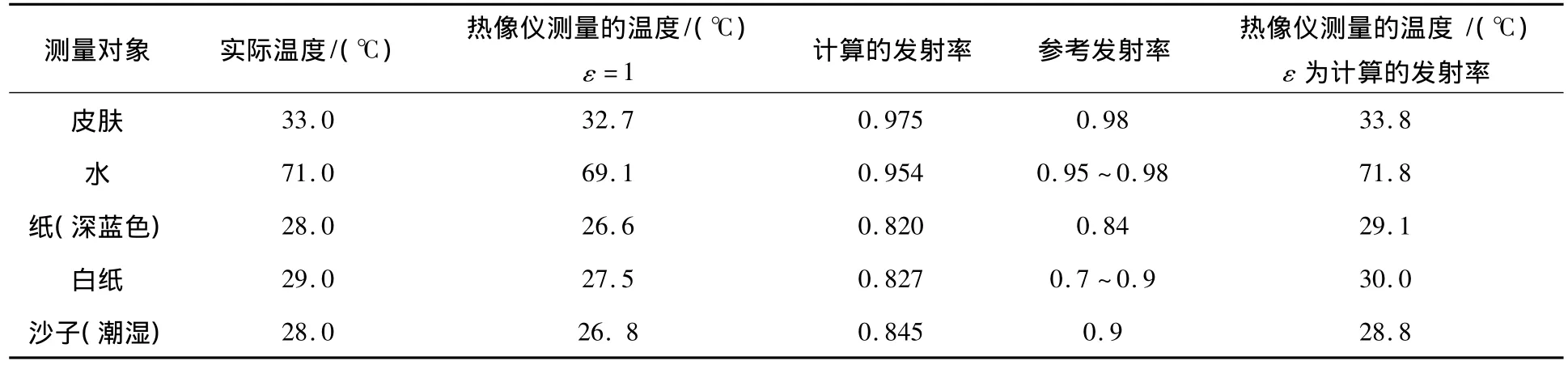
表1 方法一的实验结果

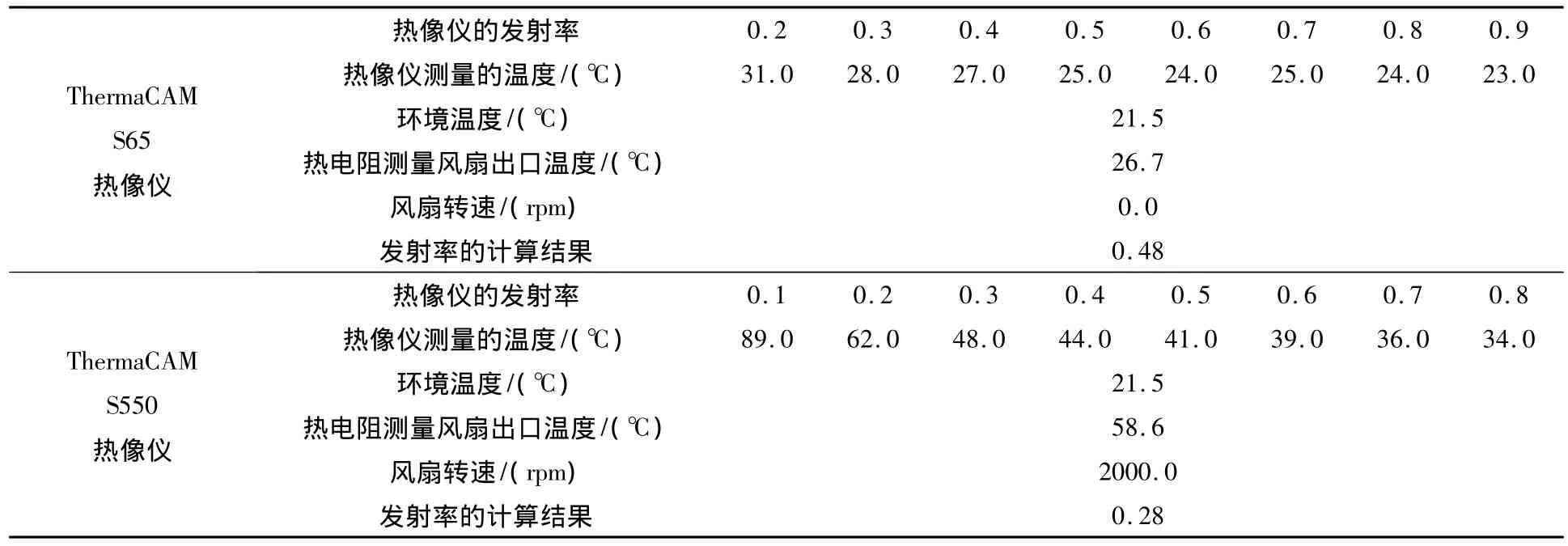
表2 方法二的实验结果(滑油风扇出口温度)

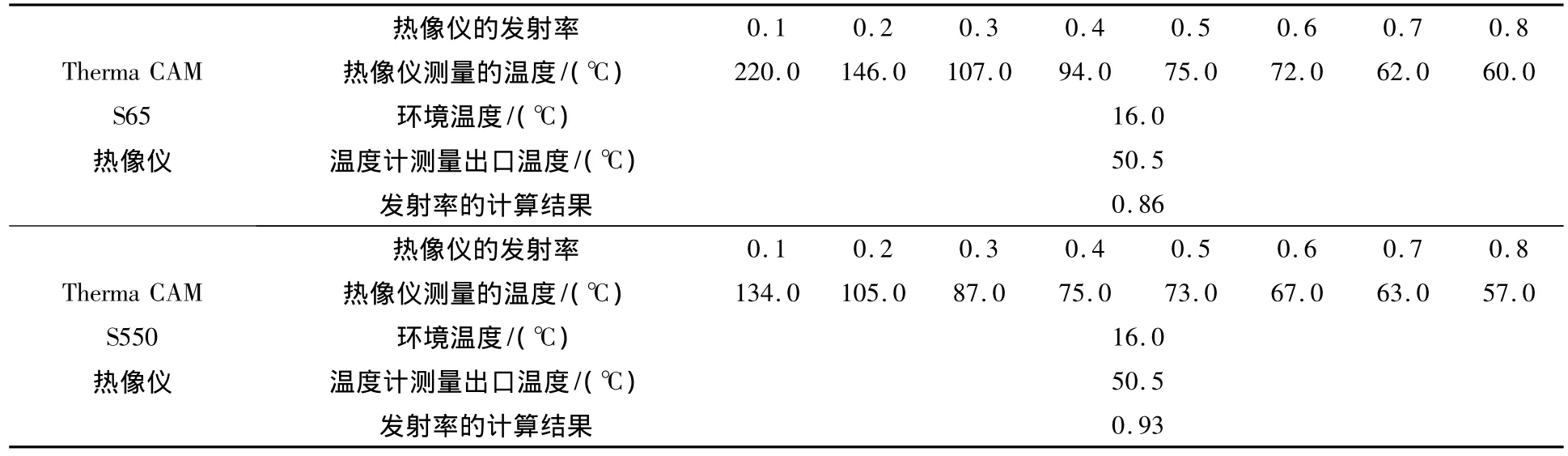
表3 方法二的实验结果(空调出口温度)

图4 空调测温热像图

4 结束语

本文从热像仪的测温原理着手，得出热像仪的测温公式，通过对测温公式进行变换，获得计算发射率的方法，所提出的计算方法简单可行，在工程实际中容易实现。

图5 散热器测温热像图

［1］董其国，编.红外诊断技术在电力设备中的应用［M］.北京:机械工业出版社，1998.

［2］杨立.红外热像仪测温计算与误差分析［J］.红外技术，1999，(4):20-24.

［3］吴晗平.红外辐射大气透射率的工程理论计算方法研究［J］.光学精密给出，1998，6(4):35-43.

［4］刘景生.红外物理［M］.北京:兵器工业出版社，1992.

［5］张鸣平，等.夜视系统［M］.北京:北京理工大学出版社，1993.