一类含有多重非线性项的双重退化抛物型方程组正解存在性

葛岩岩,王 建＊＊,庞润宏

(1.中国海洋大学数学科学学院,山东青岛266100;2.东宁电业局,黑龙江牡丹江157200)

一类含有多重非线性项的双重退化抛物型方程组正解存在性

葛岩岩1,王 建1＊＊,庞润宏2

(1.中国海洋大学数学科学学院,山东青岛266100;2.东宁电业局,黑龙江牡丹江157200)

本文主要讨论了含有内部源和非线性边界流耦合的双重退化非线性抛物型方程组解的整体存在和爆破性质,在合理的假设下,通过比较原理得到该方程组的所有正解整体存在的充分必要条件。

双重退化抛物型方程组;全局存在性;爆破;内部源;非线性边界流

0 引言

本文主要考虑下面含有非线性内部源和边界流的双重退化抛物型方程组:

其中ni,q11,q12,q21,q22>0,mi,pi>1(i=1,2)。抛物方程组(1)来源于人口动力学,化学反应,热传导等数学模型中。特别地,这类方程组经常用来描述在多方条件下与位移速度的切向张力幂相关的多孔介质中的非稳定流。此时,方程组(1)称为非牛顿多方渗流方程组[1-3],当mi,pi>1(i=1,2)时,方程组具有双重退化性。另外,非线性边界条件物理上可以解释为一种非线性辐射定律[4]。

近几年,许多人研究了带有非线性边界条件的一些抛物问题的解的整体存在性和爆破性[5-9]。

在文献[5]中G.Acosta和J.D.Rossi研究了高维非退化情形下解的整体存在性和爆破性,此即方程组(1)中mi,pi=1(i=1,2),x∈Ω情形。在文献[6]中, Song和Zheng考虑了下面的拟线性抛物方程组:

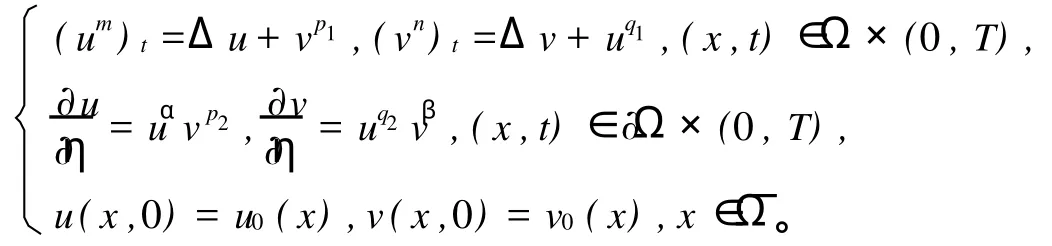
S.Wang[7]和J.Zhou,C.L.Mu[8]分别研究了不含局部源的非牛顿多方渗流方程组的非线性边值问题和含局部源的非牛顿多方渗流方程组的Dirichlet边值问题。在文中作者证明了解局部存在性并且得到了所有正解整体存在及在有限时间内爆破的性质主要依赖于初值以及α β和mn(p-1)(q-1)的关系。

最近,Wu和Gao[9]研究了下面带有非局部源的发展的p-Laplace方程组:

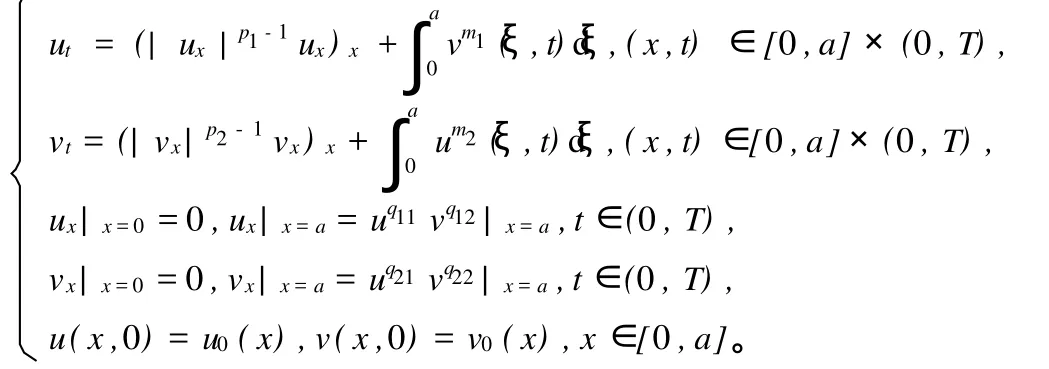
作者在文中得到了所有正解整体存在的充分必要条件为:

m1m2≤1,p1p2q12q21≤(1-p1q11)(1-p2q22),

m1p2q21≤1-p2q22和m2p1q12≤1-p1q11。

受到文献[9]的启发,本文研究了方程组(1)的解的整体存在性以及爆破性质,并给出解的性质依赖于相关参数p1,p2,q11,q12,q21,q22,m1,m2,n1,n2之间的关系。

本文主要结果如下。

定理1 问题(1)的所有正解整体存在的充分必要条件是n1n2≤1,n1p2q21≤1+(1-m2)p2-p2q22,n2p1q12≤1+(1-m1)p1-p1q11和p1p2q12q21≤[1+(1-m1)p1-p1q11][1+(1-m2)p2-p2q22]。

定理2 如果下列不等式之一成立,

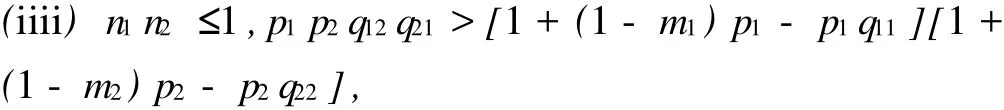
则问题(1)的所有正解在有限时间内爆破。

1 预备知识

问题(1)的解的局部存在性的证明是标准的,可参见文献[1-3]和文献[9]。

2 定理的证明

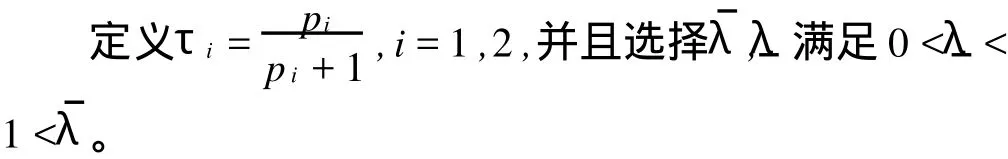
引理1 如果n1n2≤1,p1p2q12q21≤[1+(1-m1)p1-p1q11][1+(1-m2)p2-p2q22],n1p2q21≤1+(1-m2)· p2-p2q22并且n2p1q12≤1+(1-m1)p1-p1q11则问题(1)的所有正解整体存在。

证明 设

由l1,l2,d,l满足的条件以及比较原理可知(u,v )是(1)的上解,这也意味着(1)的解整体存在。

引理2 对于n1n2>1,则问题(1)的所有正解在有限时间爆破。

证明 由简单的证明可知存在ki>0,i=1,2,使得

[1] Kalashnikov A S.Some problems of the qualitative theory of nonlinear degenerate parabolic equations of second order[J].Russ Math Surv, 1987,42(2):169-222.

[2] Vazquez J L.The porous medium equations:Mathematical theory [M].Oxford:Clarendon Press,2007.

[3] Wu Zhuoqun,Zhao Junning,YinJingxue,et al.Nonlinear diffusion equations[M].River Edge:NJ:World Scientific Publishing Co,2001.

[4] Filo J.Diffusivity versus absorption though the boundary[J].Journal of Differential Equations,1992,99(2):281-305.

[5] Acosta G,Rossi J D.Blow-up versus global existence for quasilinear parabolic systems with a nonlinear boundary condition[J].Z Angew Math Phys,1997,48(5):711-724.

[6] Song Xianfa,Zheng Sining.Blow-up analysis for a quasilinear parabolic system with multi-coupled nonlinearities[J].J Math Anal Appl, 2003,281(2):739-756.

[7] Wang Shu.Doubly nonlinear degenerate parabolic systems with coupled nonlinear boundary conditions[J].J Differential Equations,2002,182 (2):431-469.

[8] Zhou Jun,Mu Chunlai.Global existence and blow-up for non-newton polytropic filtration system coupled with local source[J].Glasgow Math J,2009,51(1):39-47.

[9] Wu Xuesong,Gao Wenjie.Global existence and blow-up of solutions to an evolution p-Laplace system coupled via nonlocal sources[J].J Math Anal Appl,2009,358(2):229-237.

Abstract: This paper studys the global existence and blow-up of solutions of doubly degenerate parabolic system coupled with local source and nonlinear boundary flux.Under appropriate hypotheses,by a weak comparison principle,necessary and sufficient conditions on the global existence of all positive solutions are obtained.

Key words: doubly degenerate parabolic system;global existence;blow-up;local source;nonlinear boundary flux

AMS Subject Classifications: 35A01;35B51;35B44;35D30

责任编辑 朱宝象

Existence of Positive Solutions for A Class of Doubly Degenerate Parabolic System with Multi-Coupled Nonlinearities

GE Yan-Yan1,WANGJian1,PANG Run-Hong2
(1.School of Mathematical Science,Ocean University of China,Qingdao 266100,China;2.Dongning Electric Power Bureau,Mudanjiang 157200,China)

O175.26

A

1672-5174(2011)06-125-05

国家自然科学基金项目(10371050);高校基本科研业务费青年教师科研专项基金项目(201113008)资助

2010-06-30;

2011-03-23

葛岩岩(1987-),女,硕士生。E-mail:geyanyan19871987@163.com

E-mail:pdejwang@163.com