转移矩阵未知时带乘性噪声系统的自适应滤波算法
褚东升,刘 祺,张 玲
(中国海洋大学工程学院,山东青岛266100)
转移矩阵未知时带乘性噪声系统的自适应滤波算法
褚东升,刘 祺,张 玲
(中国海洋大学工程学院,山东青岛266100)
针对带乘性噪声系统状态转移矩阵未知的情况,提出1种在线性最小方差意义下的系统参数和状态联合滤波算法。以迭代方式获得模型参数和系统状态的递推估计:首先,利用之前时刻的状态估计值,根据投影定理,对系统未知参数即系统状态转移矩阵作出估计;其次,利用已得到的系统参数估计值,获取当前时刻的状态滤波。计算机仿真结果表明了算法的有效性。
乘性噪声;转移矩阵;自适应滤波;线性最小方差估计
自Kalman滤波方法提出以来,在信号估计领域取得了众多的理论成果,并在空间技术、通讯、导航等许多领域得到了广泛应用[1-3]。但在使用Kalman滤波解决实际问题时的1个很大限制是必须预先知道模型的参数或其统计性质,如系统初始值、各模型参数矩阵、噪声的统计特性等。而实际中这些参数往往是未知的,或近似已知的,或部分已知的:这常常导致大的状态估计误差,甚至会使滤波器发散[1]。因此,对自适应Kalman滤波的研究十分必要。另外,在许多实际观测过程中,如石油地震勘探、通讯工程、语音处理等,往往需要考虑系统的时变性、非线性畸变、能量衰减等各种复杂甚至不确定因素。这些因素在数学上可以近似归结为乘性噪声[4]。此类估计问题的难点在于,由于乘性噪声的引入,系统量测方程不再是线性的。近年来,这种带乘性噪声系统的滤波问题已经引起人们的极大关注[4-8]。
目前,针对不带乘性噪声随机线性系统的自适应滤波算法的理论与应用研究已经取得了较丰富的成果[9-14],其中,文献[11]讨论了当系统模型矩阵、噪声方差矩阵和初值向量中含有未知参向量时的线性估计。文献[12]讨论了状态空间规范形式下转移矩阵与控制矩阵含有未知参数时的参数估计和联合滤波。文献[13]给出了一种将未知参数作为扩展状态,借助非线性滤波对状态空间模型进行线性化处理,并利用扩展Kalman滤波对模型转移矩阵进行估计的方法。但该方法只适用于转移矩阵为单常数的情况,且是在不带乘性噪声的条件下进行的。文献[14]给出了控制矩阵和初值含未知参向量时情况下的估计公式,并给出了严格的证明。
在带乘性噪声系统自适应滤波的研究上,文献[6]提出了1种参数和状态预报估计的两段互耦式算法,并以石油勘探领域中的地震道模型为例,对其参数辨识方法进行了详细推导。文献[17]对带乘性噪声系统在乘性噪声及其统计参数未知的情况下,基于极大似然准则,提出了1种分块组合优化估计算法。
本文将针对带乘性噪声系统,研究状态转移矩阵的递推估计方法及其系统状态滤波。
1 问题描述
对于带乘性噪声的离散随机系统,其状态空间表达的一般形式是:
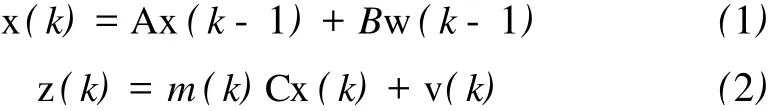
其中x(k)为n维状态向量,z(k)为q维观测向量, w(k)为h维动态噪声,v(k)为q维观测噪声。A∈Rn×n为未知状态转移矩阵,B∈Rn×n、C∈Rq×n分别为相应维数的常值矩阵;m(k)为一维乘性噪声。对任意整数k≥0,j≥0,满足以下假设条件:
假设1 E{w(k)}=0,E{w(k)wT(j)}=Q(k)δkj;
假设2 E{v(k)}=0,E{v(k)vT(j)}=R(k)δkj;
假设3 E{m(k)}= ̄m,E{[m(k)- ̄m][m(j)- ̄m]T}= σ(k)δkj;
假设4 E{x(0)}=0,E{x(0)xT(0)}=S(0);
假设5 {m(k)}、{w(k)}、{v(k)}及{x(0)}相互统计独立。
2 一类线性模型的线性最小方差估计算法
古典最小二乘法是最为常用的参数辨识方法,且在一定条件下,加权最小二乘估计即等价于线性最小方差估计[13]。下面利用这种等价关系,以引理的形式给出一类线性模型的线性最小方差估计算法。
引理1[13]对于如下线性模型:
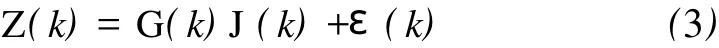
其中Z(k)为量测向量,G(k)为相应维数的已知矩阵, J(k)为未知参向量,ε(k)为随机噪声向量且ε(k)相互独立即E{ε(k)}=0,E{ε(k)εT(j)}=V(k)δkj。
有J(k)的线性最小方差无偏估计为:

本文将在以上引理的基础上,对系统(1)和(2)中的未知转移矩阵A进行估计,并利用所得结果计算系统状态滤波值。
另外,在估计系统转移矩阵时,需要用到上一时刻系统状态滤波值,因此,在这里以引理的形式不加证明的给出带乘性噪声系统的滤波递推式。
引理2[4]满足假设条件1~5的系统(1)和(2),有如下在线性最小方差意义下的状态滤波递推算法:
状态滤波估计
^x(k)=^x(k/k-1)+K(k)(z(k)- ̄mC^x(k/k-1))
增益矩阵
K(k)= ̄m(k)P(k/k-1)CTR-1L(k)
新息方差阵
RL(k)=R(k)+ ̄m2CP(k/k-1)CT+σ(k)CS(k)CT
状态相关矩阵
S(k)=A(k/k-)S(k-1)AT(k/k-1)+BQ(k-1)BT
滤波误差方差阵为
P(k)=P(k/k-1)- ̄mK(k)CP(k/k-1)
状态一步预测
^x(k/k-1)=A(k/k-1)^x(k/k-1)
一步预测误差方差矩阵
P(k/k-1)=A(k/k-1)P(k-1)AT(k/k-1)+BQ(k-1)BT
初始值^x(1/0)=0,P(1/0)=S(0)。
3 带乘性噪声系统状态转移矩阵未知时的自适应滤波算法
下面利用之前给出的2个引理,给出线性最小方差意义下,状态转移矩阵的递推估计算法。定理 考虑系统(1)、(2),若系统满足假设条件1~5,则有系统状态转移矩阵在线性最小方差意义下的如下递推估计算法。

证明 首先,对(1)式进行改写:

其中,Vec(A)是对矩阵A按列向量依次排成的向量,即矩阵向量化运算[15]。
将(8)式代入(2)式得

其中,“⊗”即为矩阵的Kronecker乘积运算[15]。
在(9)式中,令H(k)=mT(k)x(k-1)=m(k)x(k-1)
根据投影定理[16]有

其中^x(k-1)由引理2的状态滤波递推式得到。
将(10)式代入(9)式得

为证明方便,令
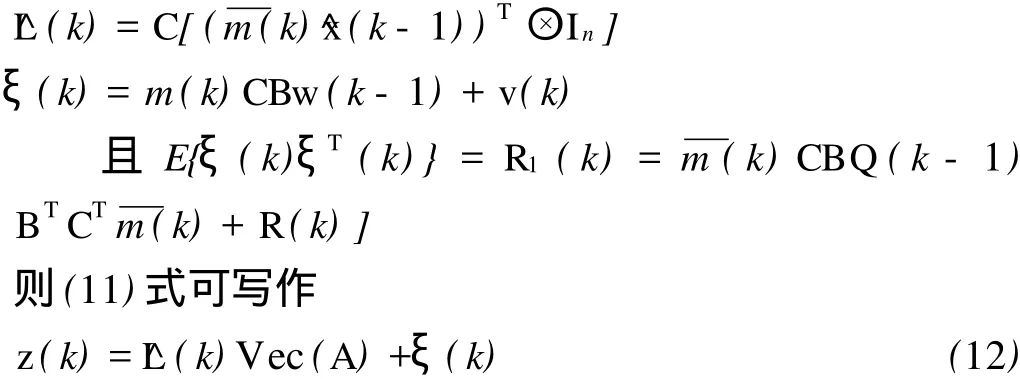
其中,^L(k)已知,Vec(A)为未知参向量,ξ(k)为噪声向量。
将(12)式与(3)式类比,由(4)式可得未知参向量Vec(A)的线性最小方差无偏估计如下:
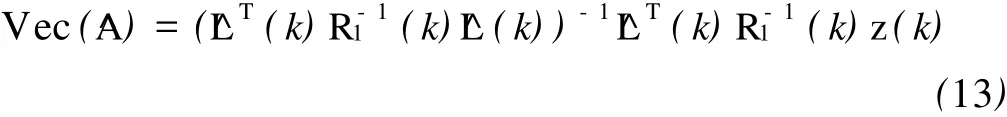
为方便利用计算机计算,将(13)式化作像Kalman滤波那样逐步递推的形式[11]
取k=1,2,…,n,合并写作

此即(5)式。
用(20)式替换(17)式中相关项,即得(7)式。
至此,定理证毕。
将由以上定理得出的转移矩阵估计值代入引理2,即可对(1)和(2)式所描述的带乘性噪声系统进行状态滤波估计,得到的滤波值用于下一时刻对状态转移矩阵的估计运算,即两者互为条件。如此递推下去,即得到系统状态滤波与状态转移矩阵的迭代滤波算法。
4 数值仿真
针对(1)和(2)式所描述的带乘性噪声系统模型,作者对本文提出的转移矩阵未知情况下的状态滤波算法进行了大量的仿真研究,并且下面以状态向量为二维的系统为例,给出仿真结果。各参数设置如下:
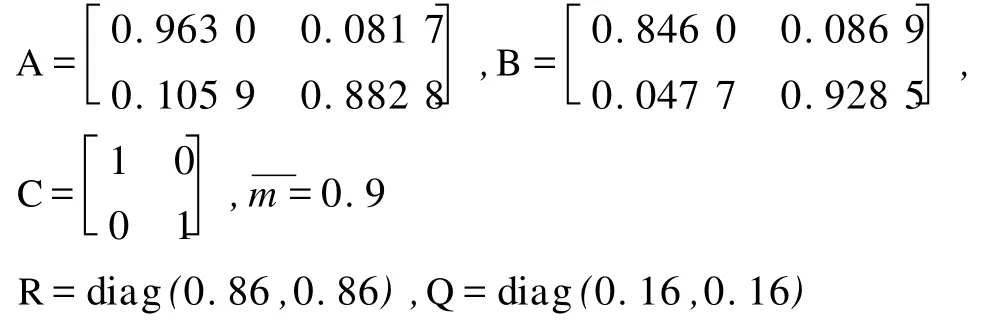
图1 二维状态转移矩阵各元素估计值Fig.1 The estimate of the elements of the transfer matrix
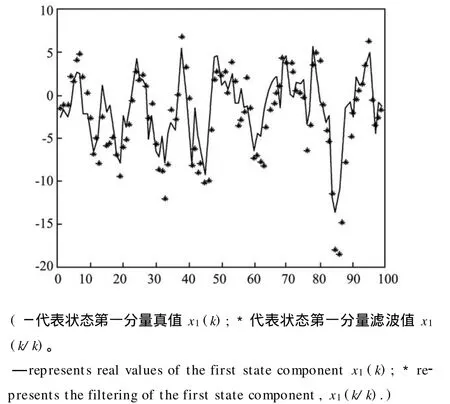
图2 状态第一个分量的滤波Fig.2 The filtering of the first state component
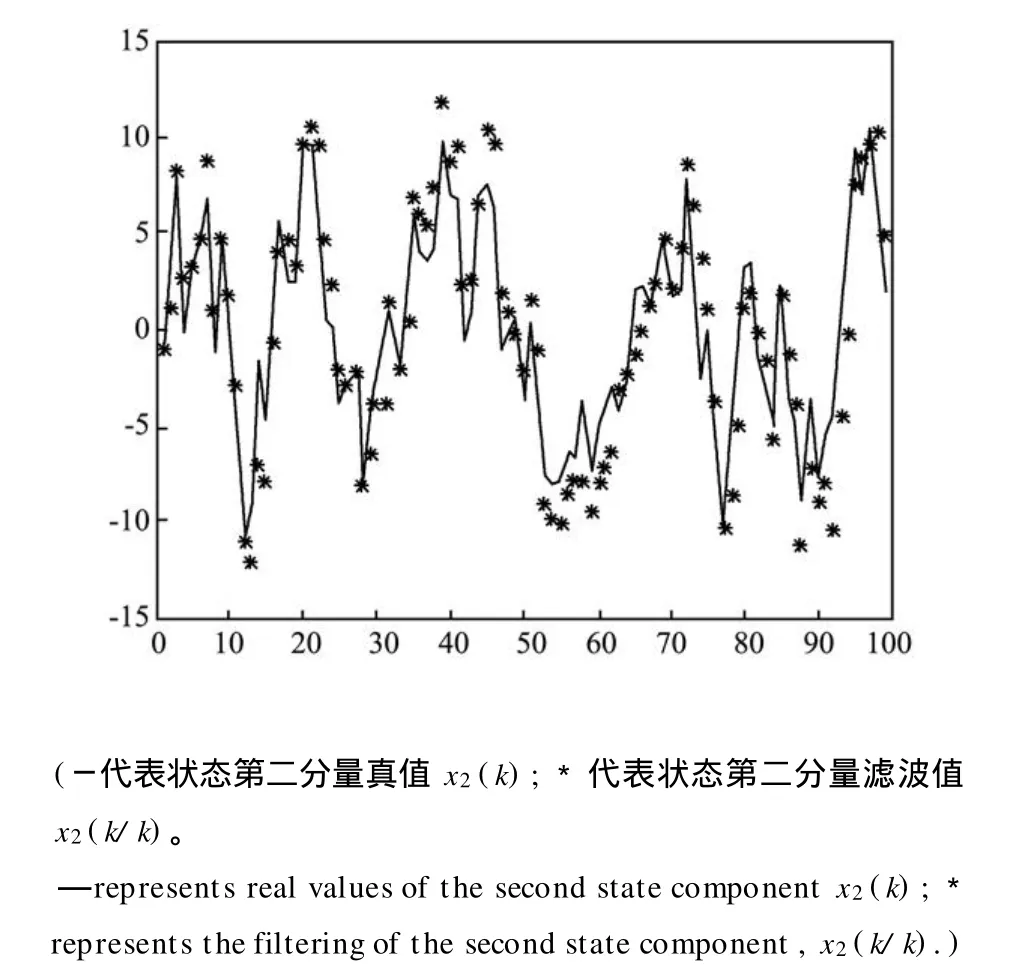
图3 状态第二个分量的滤波Fig.3 The filtering of the second state component
在每一时刻,基于上一时刻的滤波结果,估计当前时刻转移矩阵,并利用所得估计值,对系统当前时刻状态进行滤波估计。仿真效果如图1~3所示。图1中,对转移矩阵的估计很快趋于稳定,为便于更清晰的进行观察,在这里只取前一半时刻的估计结果。
5 结语
本文针对1种转移矩阵未知情况下的带乘性噪声系统,在其状态滤波估计的基础上,给出了转移矩阵在线性最小方差意义下的估计算法,并将算法化作了便于计算机实现的递推形式,实现了系统状态滤波与状态转移矩阵之间的迭代估计,从而形成了带乘性噪声系统在状态转移矩阵未知情况下的1种自适应滤波算法。仿真结果表明了算法的有效性。
[1] Lewis F L,Xie L,Popa D.Optimal and robust estimation:with an introduction to stochastic control theory[M].NY:CRC Press,2008.
[2] Fan Wang,V Balakrishnan.Robust Kalman filters for linear timevarying systems with stochastic parametric uncertainties[J]. IEEE Trans on Signal Processing,2002,50(4):803-813.
[3] 付梦印,邓志红,阎莉萍.卡尔曼滤波理论及其在导航系统中的应用[M].北京:科学出版社,2010.
[4] Rajasekaran P K,Satyanarayana N,Srinath M D.Optimum linear estimation of stochastic signals in the presence of multiplicative noise[J].IEEE Trans Aerosp Electron Syst,1971,AES-7 462-468.
[5] Chow B S,Birkemeier W P.A recursive estimator that uses data in blocks with application to time invariant systems with multiplicative noise[C].USA:Proc IEEE Int Symp Circuits and Syst, 1987:98-101.
[6] 褚东升.带乘性噪声系统的估计理论与应用[D].哈尔滨:哈尔滨工业大学,1994.
[7] Primbs J A.Stochastic receding horizon control of constrained linear systems with state and control multiplicative noise[C].New York:2007 American Control Conference,2007:4470-4475.
[8] 褚东升,张征.带乘性噪声的一类非线性系统的滤波算法[J].中国海洋大学学报:自然科学版,2006,36(4):569-572.
[9] Shiuh-Ku Weng,Chung-Ming Kuo,Shu-Kang Tu.Video object tracking using adaptive Kalman filter[J].Journal of Visual Communication and Image Representation,2006(6):1190-1208.
[10] Dimitris G,Manolakis,Vinay K,et al.Statistical and Adaptive Signal Processing[M].Beijing:Tsinghua University Press, 2003.
[11] Nahi N E,Knobbe E J.Optimal liner recursive estimation with uncertain system parameters[J].IEEE Transactions on Automatic Control,1976(4):263-266.
[12] 丁峰,谢新民.系统参数和状态联合估计[J].控制与决策, 1994,9(3):223-225.
[13] 中国科学院数学研究所概率组.离散时间系统滤波的数学方法[M].北京:国防工业出版社,1975.
[14] 汪咬元.量测方程中合有参向量的递推滤波[J].系统工程学报,1995,72-84.
[15] 王松桂.线性模型的理论及其应用[M].合肥:安徽教育出版社,1999.
[16] 邓自立.最优估计理论及其应用[M].哈尔滨:工业大学出版社,2005.
[17] 张文林,褚东升,侯永海.带乘性噪声系统的极大似然最优估计算法[J].青岛海洋大学学报,1999,29(2):332-338.
Abstract: In the sense of linear minimum-variance,this paper develops a corresponding recursive algorithm for stochastic linear systems with multiplicative noise whose transfer matrix is unknown.That is to say,estimations of parameters and states are obtained by the way of iteration.First,according to projection theorem,the system parameters are estimated by the using of the state estimation of previous moment.Then,based on the estimation of the system parameters,the optimal filtering of the current moment is obtained.Simulations are illustrated to show the validity of the algorithms.
Key words: multiplicative noise;transfer matrix;adaptive filtering;linear minimum-variance estimation
责任编辑 陈呈超
Adaptive Estimation Algorithm for Systems with Multiplicative Noise and Unknown Transfer Matrix
CHU Dong-Sheng,LIU Qi,ZHANG Ling
(College of Engineering,Ocean University of China,Qingdao 266100,China)
TP31
A
1672-5174(2011)06-115-05
国家自然科学基金项目(60704023)资助
2010-10-26;
2010-12-16
褚东升(1956-),男,教授。E-mail:chuds@yahoo.cn

