新五维超混沌Lorenz 系统

柳 妮

(四川文理学院物理与工程技术系，四川 达州 635000)

1963年，美国气象学家Lorenz构造了著名的混沌Lorenz系统模型，开创了科学家研究混沌的先河.继 Lorenz后，研究者构造出了混沌Rossler系统、混沌Chua电路系统、混沌Chen系统、混沌Lü系统和混沌Liu系统等著名的三维自治混沌系统，并且将这些系统广泛应用于保密通信、控制工程、生物工程等领域.然而，这些三维自治混沌系统只有一个正的Lyapnov指数，其动力学行为不足够复杂，吸引子结构比较简单.随着计算机的高速发展，短期预报、神经网络预测等攻击方法的进步，三维混沌系统在信息安全、保密通信等工程中的应用，其优势越来越遭到削弱.近年来，许多研究者把目光集中在能产生两个正的Lyapunov指数的四维超混沌系统研究上，出现一大批新的超混沌系统，例如超混沌Lorenz系统、超混Rossler系统、超混沌 Chen系统、超混沌 Liu系统和超混沌 Qi系统［1－15］及其电路实现等.

从现有文献看，四维超混沌系统主要是在原有三维混沌系统基础上添加线性或非线性控制项来构造不同的超混沌系统.这些四维超混沌系统中，许多系统的特征参数使系统处于混沌状态范围远远大于使之处于超混沌状态的范围，且可能出现混沌和超混沌区域交替的现象.而在判断系统是否处于混沌状态的诸多方法中，只有李雅普诺夫指数法可以区分系统是处于混沌状态还是超混沌状态，其它的方法如功率谱法、庞加莱截面法等不能区分系统是处于混沌状态还是超混沌状态.如果一个系统处于超混沌状态的参数范围过小，那么它在外界影响下，较容易得到混沌信号，而不容易区分所得到的信号是混沌的还是超混沌的.因此，最近研究的主要目标是扩大系统处于超混沌状态的参数范围［11－12］，研究方法是改变三维系统到四维系统中加入的控制器的类型和调整不同参数，这些方法局限于四维系统，由于系统参数甚多，要得到超混沌状态范围广的参数十分不易.本文针对已有方法的不足，通过增加维数的方法，尝试构造出五维超混沌Lorenz系统，力求达到:1)扩大系统处于超混沌状态的特征参数范围;2)尽量减小或者除去系统处于混沌状态的参数范围，避免混沌与超混沌交替出现;3)从分岔图看，力求完美呈现出系统从稳定到周期、拟周期、混沌和超混沌状态的演化过程.

1 新超混沌Lorenz系统描述

文献［16］给出了一个三维超混沌Lorenz系统，系统方程为:

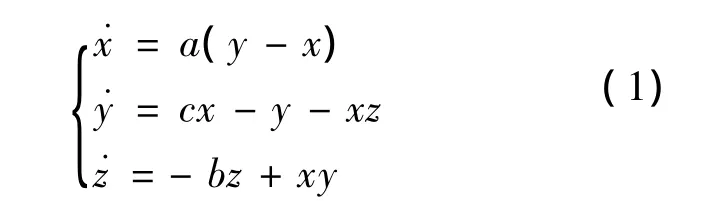
我们在系统(1)上加入一个非线性反馈控制器w到第一个方程，再加入一个线性状态控制器u到第二个方程，构成一个新的五维自治系统，以期扩大系统处于超混沌状态的范围，突显系统从平衡点到周期轨道再到拟周期、混沌和超混沌的过程.具体动力学系统方程为:

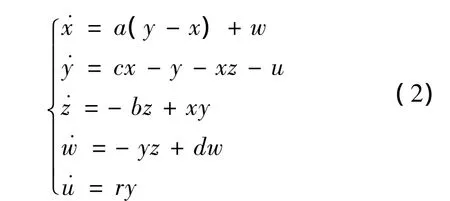
2 系统耗散性分析和系统平衡点分析

2.1 系统耗散性分析

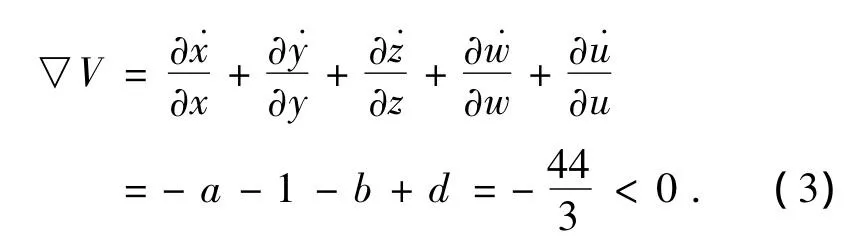
对系统(2)，有所以系统(2)是耗散系统，并且以指数速率收敛，当t→∞ 时，包含系统轨线的每个小体积元以指数速率收缩到0，最终系统所有的轨线将被限制在一个体积为0的极限点集上，并且它的渐近动力学行为会被固定在一个吸引子上，这说明混沌和超混沌吸引子存在.

2.2 系统平衡点分析

系统(2)的平衡状态方程为

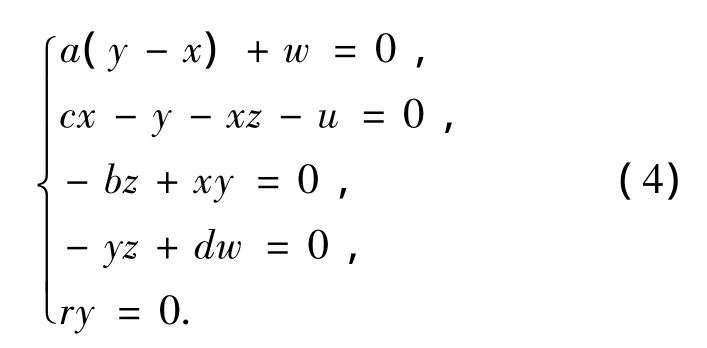
解方程组(4)可得系统唯一平衡点 S0(0，0，0，0，0)与系统的参数 a，b，c，d，r都无关.系统在平衡点S0处线性化系统(2)得到对应的Jaccobi矩阵为

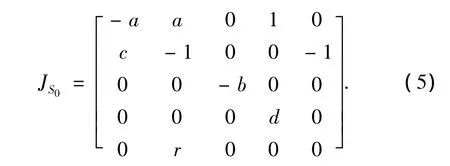
其特征值方程为

(λ +b)(d- λ)［λ3+(a+1)λ2+

(a-ac+r)λ +ar］ =0

由Routh－Hurwitz定理可知:当r＞2970时，系统将稳定于S0点;当r＜2970时，S0点是不稳定平衡点，系统可能产生混沌、超混沌吸引子、拟周期运动状态或周期运动状态.

3 系统分岔分析

众所周知，在已有混沌方法中只有Lyapunov指数方法可以准确判定系统是处于混沌还是超混沌，因此假设系统(2)的Lyapunov指数分别为λLi(i=1，2，3，4，5)且满足 λL1＞ λL2＞ λL3＞λL4＞λL5，由稳定性理论可知:λL5＜λL4＜λL3＜λL2＜λL1＜0时，系统处于稳定点;当λL5＜λL4＜λL3＜λL2＜λL1=0时，系统处于周期状态;当λL5＜λL4＜λL3＜0和λL2=λL1=0时，系统处于拟周期状态;当λL5＜λL4＜λL3＜0，λL2=0，λL1＞0和λL5+λL4+λL3+λL2+λL1＜0时，系统处于混沌状态;当λL5＜λL4＜0，λL3=0，λL2＞0，λL1＞0和λL5+λL4+λL3+λL2+λL1＜0时，系统处于超混沌状态.我们采用Wolf相空间重构法和四阶龙格－库塔法计算系统(2)的5个lyapunov指数，取系统初始值为(1，1，1，1，1)，固定系统参数 a=10，b=，c=28，d=-1，调整参数r的范围为0＜r≤35，系统随着参数r变化的lyapunov指数谱和状态x对应的分岔图如图1(a)所示.

根据图1(b)和图1(c)所示，可以得出系统(2)随参数r变化的动力学行为如下:当0＜r＜28时，系统具有2个正的Lyapunov指数，即λL1，λL2＞0，系统处于超混沌运动状态;当28＜r＜50时，系统处于拟周期运动状态;当50≤r＜2970时，系统处于周期轨道;当r＞2970时，系统处于平衡点.

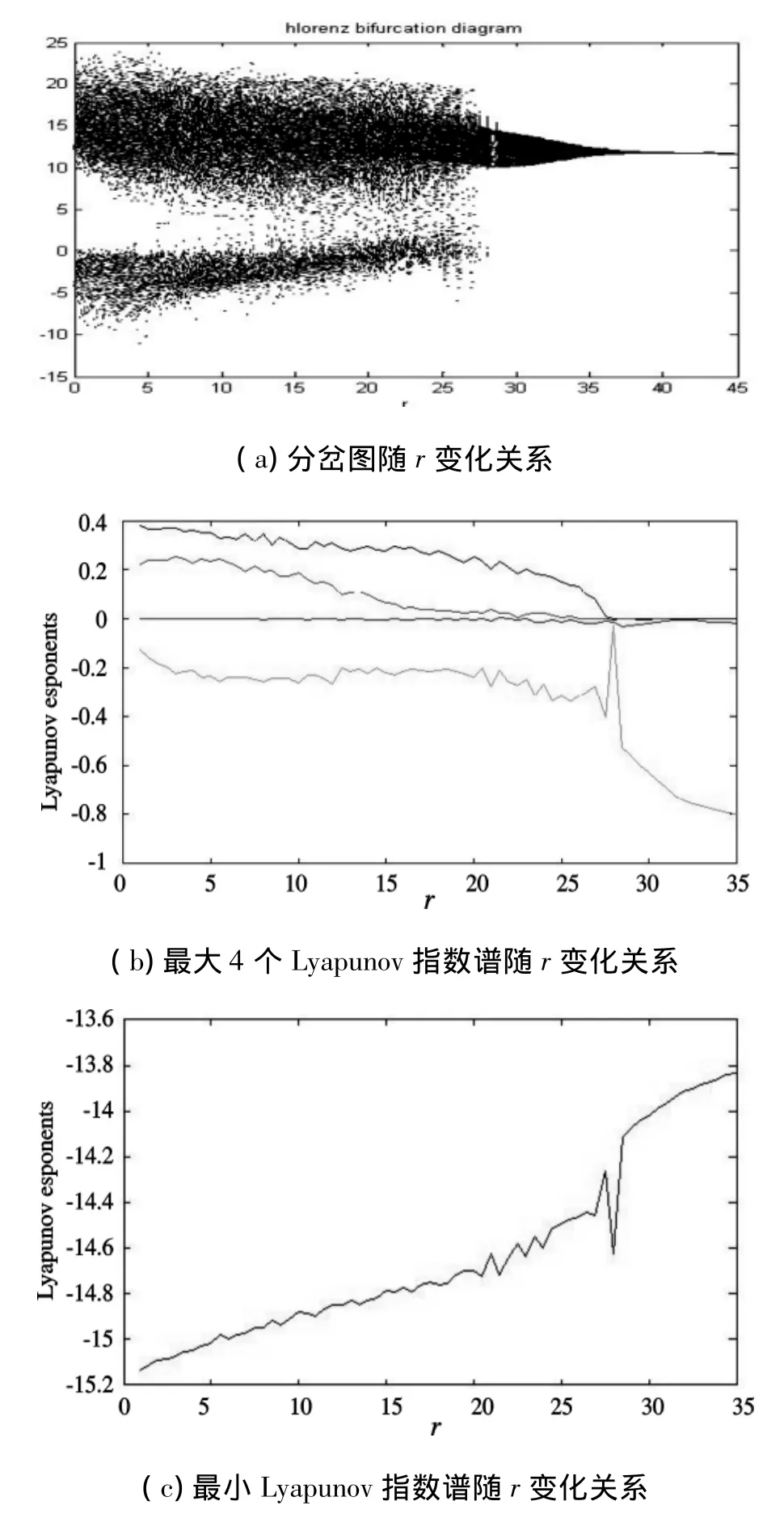
图1 当 a=10，b=8/3，c=28，d= －1，0 ＜r＜35时，系统(2)的分岔图和Lyapunov指数谱

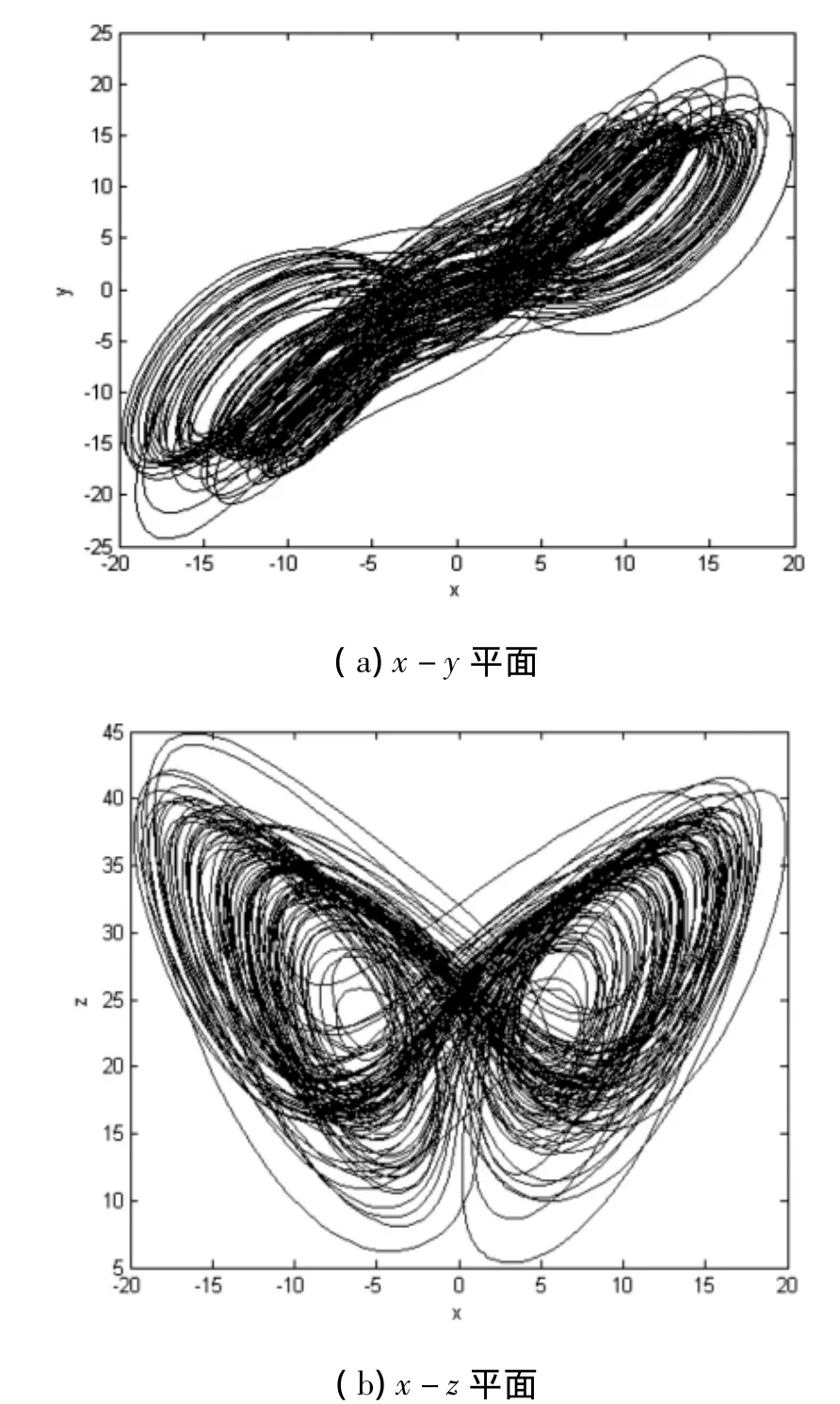
图2 当 a=10，b=8/3，c=28，d= －1，r=10 时系统(2)处于超混沌状态时的相轨迹图

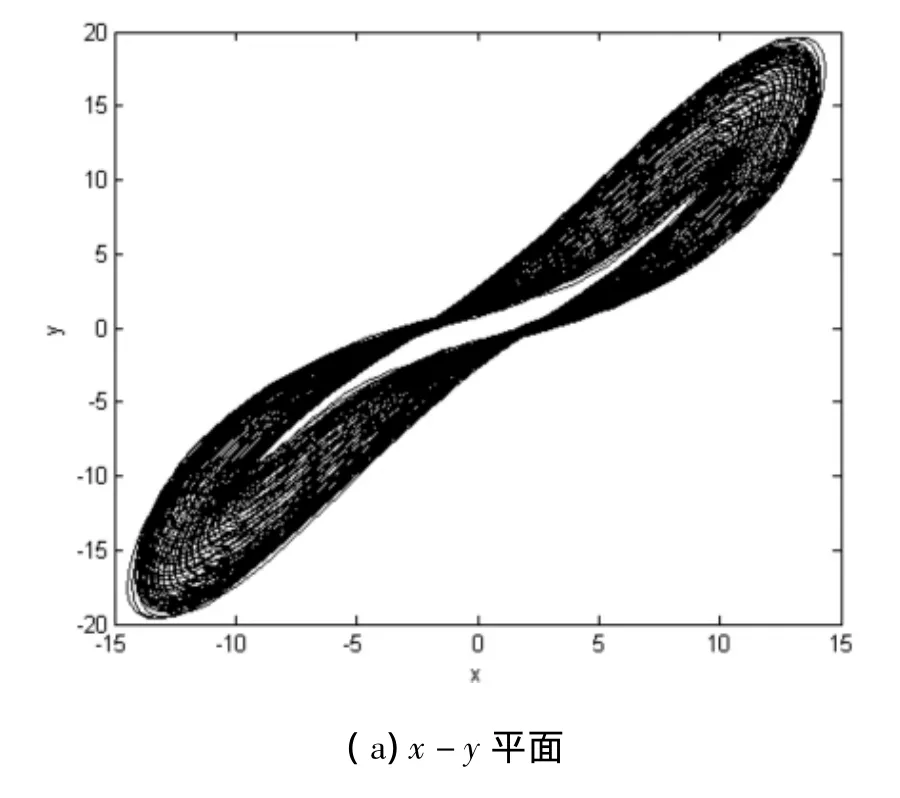
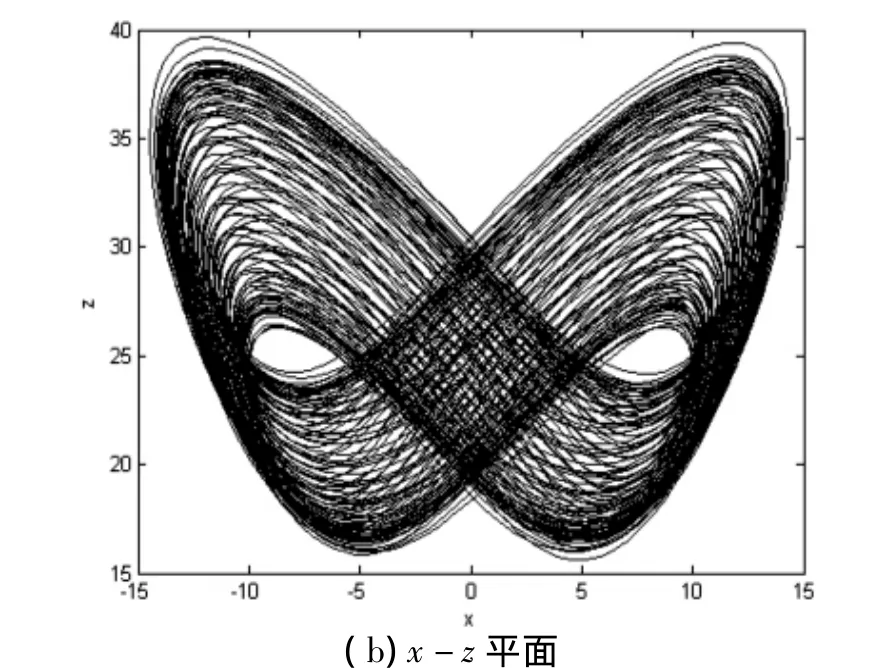
图3 当 a=10，b=8/3，c=28，d= －1，r=30 时系统(2)处于拟周期状态时的相轨迹图

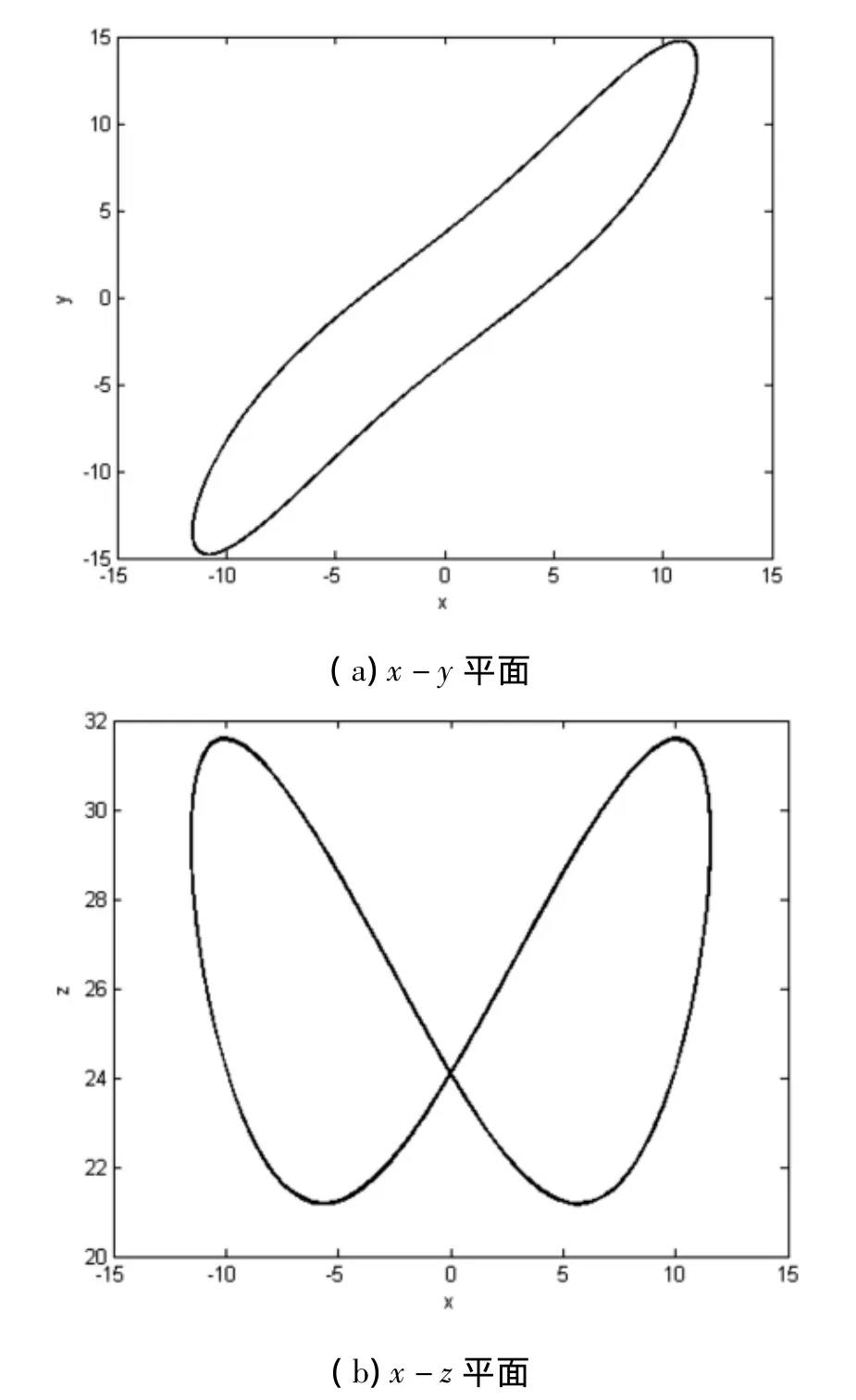
图4 当 a=10，b=8/3，c=28，d= －1，r=52 时系统(2)处于周期状态时的相轨迹图

4 结语

本文在四维自治动力学系统中加入线性反馈控制器构造出五维自治超混沌动力学系统，通过对系统的动力学耗散性、平衡点性质和分岔行为等分析发现:1)五维超混沌系统具有很宽的使系统处于超混沌状态的特征参数范围，仅有很小的参数范围使系统处于混沌状态，在实际应用中可以避免系统误差产生的混沌信号和超混沌信号而难以区分的困难;2)系统从平衡点到周期状态、拟周期状态、混沌状态，进而到超混沌状态，过程十分明显，没有出现互相交替的现象，是一个完美的动力学演变过程，处于拟周期状态的参数范围较大;3)这种方法对其它要产生较宽超混沌范围和较小的混沌范围的系统具有一定的借鉴意义.

［1］QiGuoyuan，Michael Antonie van Wyk.On a new hyperchaotic system ［J］.Physics Letters A，2008，372(1):124－136.

［2］Qi Guoyuan，Du Shengzhi，Chen Guanrong，etal.On a four－dimensional chaotic system［J］.Chaos Solitons ＆Fractals，2005，23(10):1671 －1682.

［3］Hu Guosi.A hyperchaotic system with a four－ wing attractor［J］.International of Modern Physics C，2009，20(2):323－335.

［4］Yang Qigui，Zhang Kangming，Chen Guanrong.Hyperchaotic attractors from a linearly controlled Lorenz system［J］.Nonlinear Analysis，2009，10(12):1601 －1617.

［5］Wang Guangyi，Zhang Xun，Zheng Yan，et al.A new modified hyperchaotic Lü system［J］.Physica A，2006，371(2):260－272.

［6］Dong Enzeng，Chen Zaiping，Chen Zengqiang，et al.A novel four－wing chaotic attractor generated from a three－dimensional quadratic autonomous system［J］.Chinese Physics，2009，18(7):2680 －2689.

［7］Wang Faqiang，Liu Chongxin.Hyperchaos evolved from the Liu chaotic system［J］.Chinese Physics，2006，15(5):963－969.

［8］Wang Jiezhi，Chen Zengqiang，Yuan Zhuzhi.The generation of a hyperchaotic system based on a three－dimensional autonomous chaotic system ［J］.Chinese Physics，2006，15(6):1216 －1225.

［9］周平，危丽佳，程雪峰.只有一个非线性项的超混沌系统［J］.物理学报，2009，58(8):5201 －5208.

［10］王繁珍，齐国元，陈增强.一个四翼混沌吸引子［J］.物理学报，2007，56(6):3137 －3144.

［11］刘明华，冯久超.一个新的超混沌系统［J］.物理学报，2009，58(7):4457 －4463.

［12］贾红艳，陈增强，袁著祉.一个大范围超混沌系统的生成和电路实现［J］.物理学报，2009，58(7):4469－4476.

［13］唐良瑞，李静，樊冰.一个新四维自治超混沌系统及其电路实现［J］.物理学报，2009，58(3):1446－1455.

［14］Zhou Ping，Cao Yuxia，Chen Xuefeng.A new hyperchaos system and its circuit simulation by EWB［J］.Chinese Physics，2009，18(4):1394 －1398.

［15］王兴元，王明军.超混沌Lorenz系统［J］.物理学报，2009，56(9):5136 －5141.

［16］Lorenz E N.Chaotic Lorenz system ［J］.Atmos.Sci，1963，20(1):130 －137.

［17］Yan ZY.Hyperchaotic Chen systems［J］.Appl.Math.Comp.，2005，168(6):1239.

［18］Rossler O E.A new hyperchaotic systems［J］.Phys.Lett.A，1978，7(2):155.