超声换能器焦区内软组织背散射信号频移与散射子粒径的相关性研究
马 浪 郭建中 刘 波 朱铮宇
(陕西师范大学应用声学研究所 陕西省超声学重点实验室,西安 710062)
引言
传统的B型超声成像利用软组织超声背散射射频信号的幅度包络信息,没有充分地利用与组织微观结构有关的频率和相位特征信息。许多学者致力于利用超声背散射回波信号的频率和相位信息进行软组织微结构特征的研究,利用超声背散射信号的功率谱估计软组织超声特征散射子粒径、衰减系数等超声特性参数[1-9];Konofagou等发现当软组织发生应变时,其超声特征散射子出现的聚集或分开现象会导致超声背散射信号的频谱中心上偏移或下偏移,并且利用频谱中心偏移估计了软组织的应变[10]。
当生物软组织发生变异后,组织的衰减系数、弹性特性以及超声特征散射子的粒径和数浓度等都相应会发生变化。本研究针对聚焦超声源,以生物软组织超声背散射信号的传输模型为基础,研究组织超声背散射信号中心频率的偏移量与散射子粒径之间的相关性,探索影响频移量的组织特性参数和换能器参数之间的联系。通过计算机模拟实验,分析组织的衰减系数和超声特征散射子的数浓度以及聚焦超声换能器的中心频率、带宽和聚焦特性等参数对背散射信号频移量的影响。利用超声背散射信号中心频率的偏移量,估计软组织超声特征散射子的粒径等与频率有关的超声散射参数,探寻此项技术在生物软组织生理病理诊断中的应用。
1 传输模型及频移量估计方法
在非均匀结构生物软组织中,超声特征散射子的有效尺寸远小于或相当于超声波波长时,则会发生散射现象,散射波的强度与散射子的粒径有关,随着散射子粒径与波长比值的增大而加强。散射也是引起超声波在组织传播过程中衰减的重要因素之一,衰减系数与频率大致成线性增长的关系,组织的作用就相当于一个低通滤波器[11]。声信号在组织中传播时,由于组织对超声波的衰减、吸收等作用,信号中心频率会发生偏移。频谱偏移方法由Ophir等在1982年提出并应用于软组织,频谱中心已被广泛地应用于多普勒频移、衰减和背散射的测量中。1997年Quan等利用频谱偏移方法估计地震波的衰减[12];他得安等提出用背散射信号频谱中心频率的偏移量来评价松质骨的健康状况,并且通过实验得出,当松质骨表观密度增大时,背散射信号的中心频率向低频方向移动,随着年龄的增大,中心频率的位置越接近于发射超声换能器的中心频率[13]。
1.1 传输模型
对于弱聚焦超声换能器信号源,只考虑横向波的衍射影响,忽略束轴波的衍射,超声波被视为平面波入射的模型,探头的横向分辨率比较差,限制了超声诊断成像系统的分辨力和精确度。Bigelow等考虑了超声聚焦源,假设通过焦区的速度势场是稳定的三维高斯分布,忽略多次散射(即Born近似),得出随机分布的单个散射子背散射信号的电压幅度谱(收发换能器在同一位置处)可表示为[1-2]
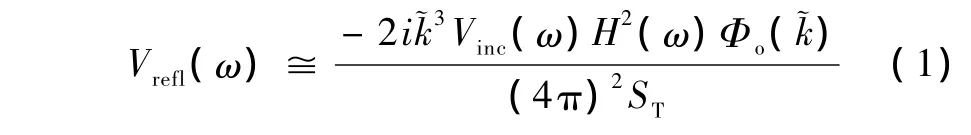
式中,ω是角频率,是超声波沿传播路径的有效复波数,ST是发射换能器的孔径面积,Vinc(ω)是用来激励发射换能器的电压项,H(ω)是换能器的频率响应函数为

式中,积分区间V’是焦区内使超声波散射的散射子分布区域,→’是球坐标系中的空间位置坐标(此球坐标系的原点在焦点处),γ(’)为密度和压缩的局部混合扰动,是表述焦区声场强度的几何衰减,其表达式为
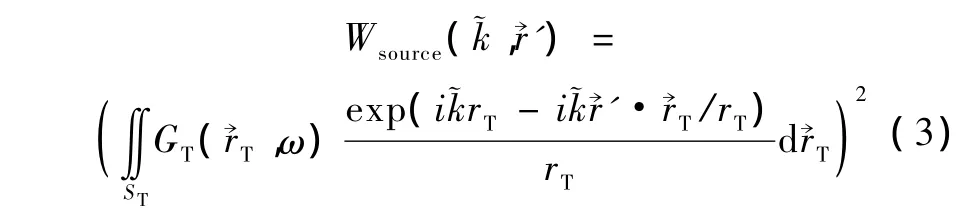
则总背散射信号的电压幅度谱就是对上述单个散射子背散射信号电压幅度谱的叠加,可表示为[2]
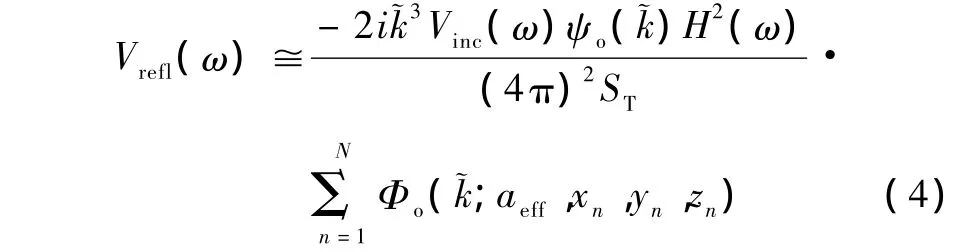
式中,N为总散射子的个数,aeff是散射子的有效平均散射半径,xn、yn、zn是散射子的位置坐标(此坐标系的原点在焦点处,z轴与束轴平行,收发换能器在z>0的区域)。
1.2 中心频率及其偏移量
假设入射超声信号为高斯型的脉冲信号,幅度谱为
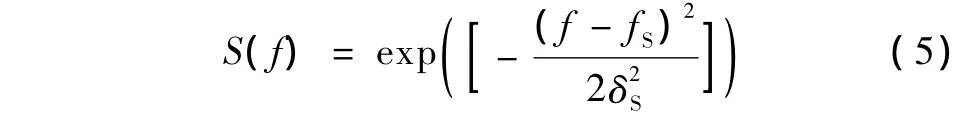
式中,f为频率,fS为入射信号的中心频率,δS2为入射信号的高斯分布方差,其中,入射信号的中心频率定义为[12]
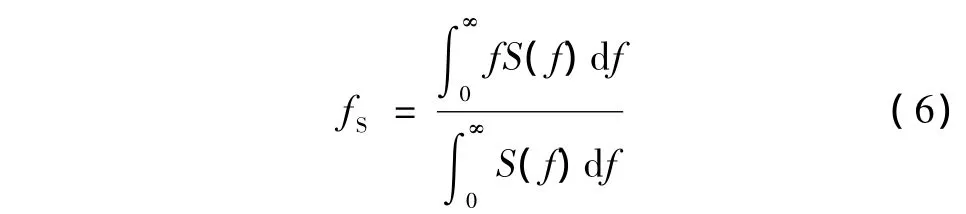
入射信号的高斯分布方差定义为
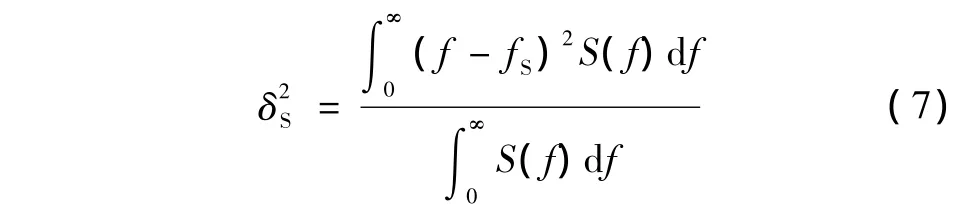
接收信号也为高斯型分布的信号,但幅度和中心频率发生了变化,其幅度谱为[12]
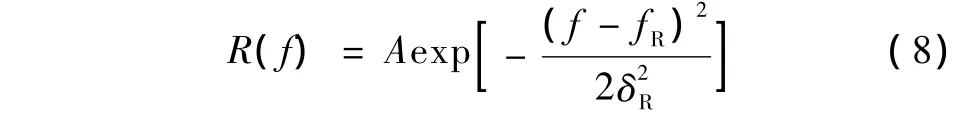
式中,A是接收信号的幅度,fR为接收信号的中心频率,δR2为接收信号的高斯分布方差,其中,接收信号的中心频率定义为[12]

接收信号的高斯分布方差定义为
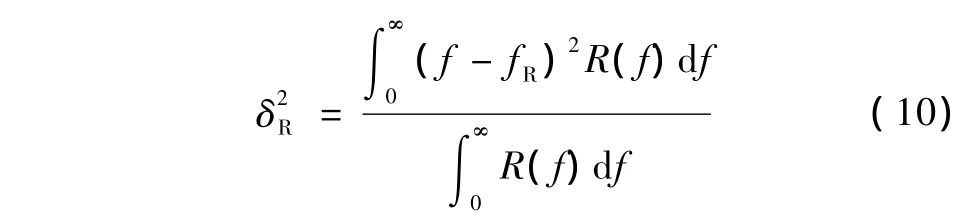
由此可得,接收信号的中心频率偏移量可表示为[12-13]
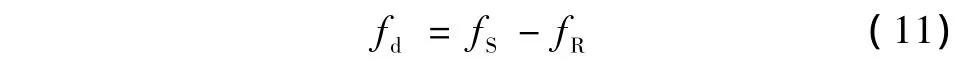
1.3 频移量估计方法
根据散射模型式(4)和中心频率的定义式可将焦区内软组织超声背散射信号的中心频率表示为
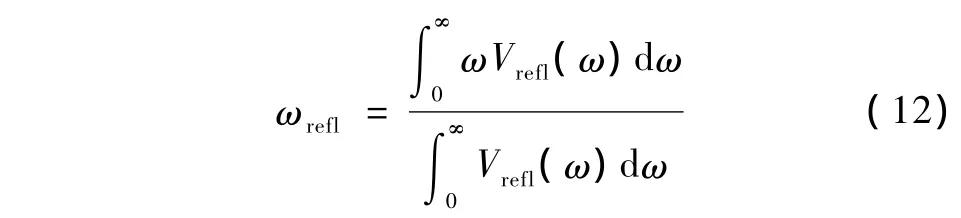
由于检测系统的传输响应也是导致超声信号中心频率发生偏移的因素之一,为了提高频移量估计的精确度,本研究在频谱估计中,从背散射信号频谱中除去检测系统传输响应对中心频率偏移的影响。检测系统传输响应由置于水中且与聚焦超声换能器焦平面平行的刚性平面板的反射回波信号中得到,刚性平面板反射回波信号的电压幅度谱为[1]
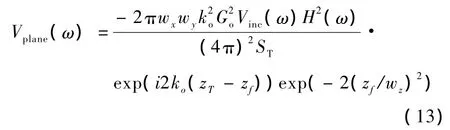
式中,ko是超声波在水中传播时的波数,wx,wy,wz是接收速度势场在焦区内的等效高斯尺寸,Go为焦区速度势场的几何增益值,zT是刚性平面板到发射换能器的距离,zf是刚性平面板到焦平面的距离。
检测系统传输响应的中心频率可表示为
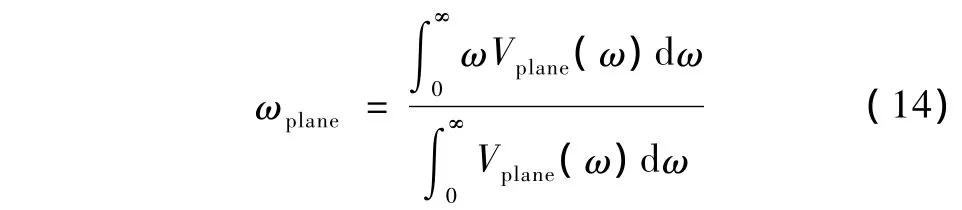
则焦区内软组织超声背散射信号中心频率的偏移量可表示为
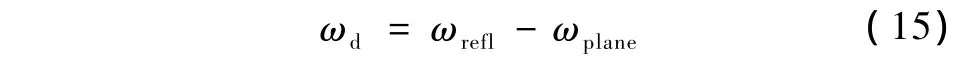
2 模拟实验方法
模拟实验过程中,组织的超声背散射信号由式(4)产生,假设为高斯散射,则对于同质组织的单个高斯散射子,Φo()可表示为[2]
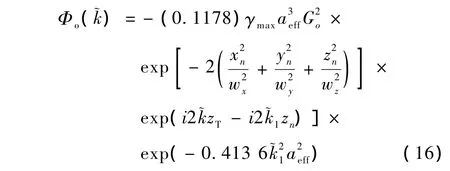
式中,γmax为γ的最大值,~1是超声波在组织中传播时的复波数。
假设超声换能器的频率响应为零频时响应为零的瑞利分布函数,即
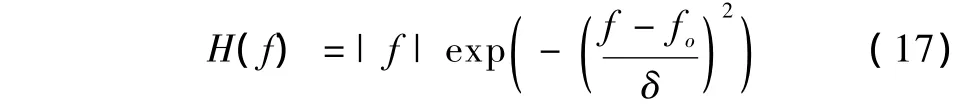
式中,fo表示换能器的中心频率,δ表示其带宽,图1是换能器的频率响应曲线。球形聚焦换能器远场的聚焦特性(f-number)由fN=F/(2a)来表征,其中,F是焦长,a是孔半径;fN越小,聚焦越强,反之聚焦越弱。
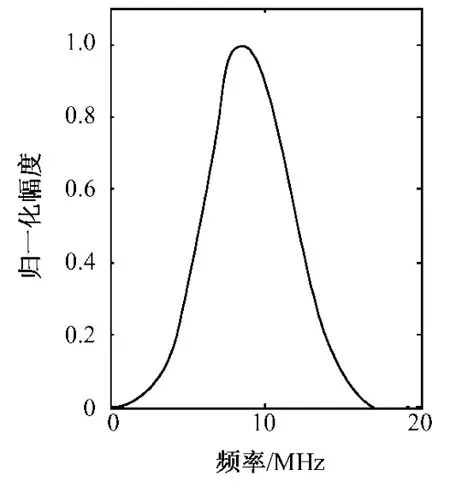
图1 换能器的频率响应曲线Fig.1 The frequency response curve of launch transducer
检测系统传输响应由式(13)产生,选择参考刚性板的位置在焦平面处,即zf=0。wx,wy,wz和Go取:wx=wy=0.87λfN;wz=6.01λ(fN)2;Go=a2/(2F)[14];λ为超声波波长。模拟过程中,假设焦长F=5cm,采样频率为50MHz,组织的差异可用有声速度、衰减系数以及密度等参数来区别,水中的声速度取为1 540m/s,水的密度为1.0g/cm3。在研究每一种参数条件下,组织超声背散射信号中心频率的偏移量与散射子粒径之间的相关性时,散射子的有效平均散射半径aeff的范围为5~55μm,为了保证模拟结果的准确性,对每一种半径aeff,由式(4)模拟10次背散射信号,然后采用统计的方法计算出平均中心频率,再根据式(15)从平均中心频率中除去检测系统传输响应的影响,即为该半径散射子相对应的频移量。
2.1 组织的衰减系数对背散射信号频移量的影响模拟
分别选择软组织为肌肉、肝和脂肪,其特性参数如表1所示,换能器的中心频率和带宽分别为8MHz和4MHz,fN=4,散射子数浓度为25/mm3。
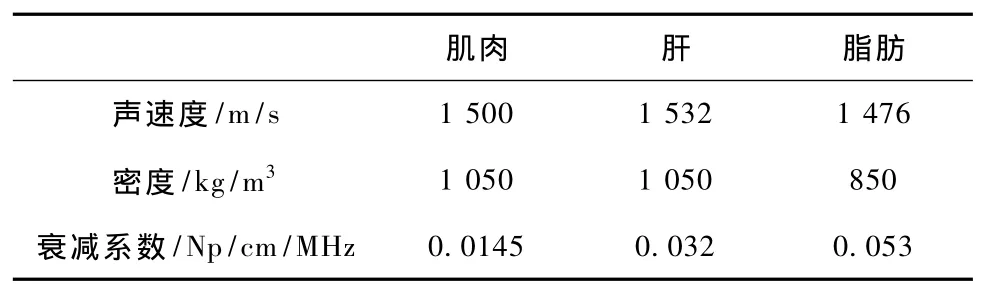
表1 组织的特性参数[15-17]Tab.1 Property parameters of tissues
2.2 换能器的中心频率、带宽和聚焦性对背散射信号频移量的影响模拟
组织参数选择为肝组织,散射子数浓度仍为25/mm3。在模拟换能器的中心频率对背散射信号频移量的影响时,换能器的带宽为4MHz,fN=4,中心频率分别选择了6、8、10MHz;在模拟换能器的带宽对背散射信号频移量的影响时,换能器的中心频率为8MHz,fN=4,带宽分别选择了2、4、6MHz;在模拟换能器的聚焦特性对背散射信号频移量的影响时,换能器的中心频率和带宽分别等于8MHz和2MHz,fN分别选择了1、2和4。
2.3 散射子的数浓度对背散射信号频移量的影响模拟
组织参数仍选择为肝组织,换能器的中心频率和带宽分别等于8MHz和2MHz,聚焦性fN=4,分别模拟了散射子数浓度等于25/mm3、55/mm3和85/mm3时的频移量随散射子粒径的变化情况。
3 结果与分析
3.1 组织的衰减系数对背散射信号频移量的影响
图2是发射脉冲的中心频率为8MHz,带宽为2MHz时发射脉冲、检测系统传输响应和背散射信号的模拟结果。从幅频特性图2(a)(右)可看出发射脉冲的中心频率为8MHz、3dB带宽为2MHz;根据图2(b)(左)可以看出,检测系统传输响应与发射脉冲相比其时间上有延时,相位有所变化,其功率谱图2(b)(右)的中心频率也有所变化。图3是软组织的衰减系数对背散射信号频移量的影响模拟结果,可以看出,软组织超声背散射信号中心频率的偏移量随散射子粒径aeff的增大而增加,近似呈线性增长的关系。当组织的衰减系数不相同时,背散射信号的频移量也不同,衰减系数越大的组织,背散射信号的频移量也越大。
由于生物软组织对超声信号的传输效应相当于一个低通滤波器,组织的衰减系数越大,就相当于滤波器的截止频率越小,如图4所示。图4是三种不同衰减系数的组织对超声信号传输效应的等效低通滤波和带宽为4MHz、中心频率为8MHz的换能器发射超声信号的归一化幅频特性,fd1、fd2和fd3分别是超声信号经过衰减系数为0.014 5Np/cm/MHz、0.032Np/cm/MHz和0.053Np/cm/MHz的组织散射以后中心频率的偏移量。分析图4不难得出,fd1<fd2<fd3,所以,组织的衰减系数越大,背散射信号中心频率的偏移量也越大。另外,由于散射波的强度随着散射子粒径与波长比值的增大而加强,散射加强,衰减增大,所以,频移量会随着散射子粒径的增大而增加。
3.2 换能器的中心频率、带宽和聚焦特性对背散射信号频移量的影响
图5是换能器的中心频率、带宽和聚焦特性对背散射信号频移量的影响模拟结果。图6为发射换能器不同参数时背散射信号频移量的比较。可以看出,发射换能器的中心频率越大,背散射信号的频移量也越大。图6(a)是衰减系数为0.032Np/cm/MHz的组织对超声信号传输效应的等效低通滤波和带宽为4MHz,中心频率分别为6、8、10MHz的换能器发射超声信号的归一化幅频特性,fd4、fd5和fd6分别是中心频率为6、8、10MHz的换能器发射超声信号经过衰减系数为0.032Np/cm/MHz的组织散射以后中心频率的偏移量。分析图6(a)可得:fd4<fd5<fd6,既换能器的中心频率越大,背散射信号的频移量也越大。
由图5(b)可知,相同带宽时,频移量随散射子粒径aeff的增大而增加;散射子粒径相同时,频移量随换能器带宽的增加而增大。图6(b)中是衰减系数等于0.032Np/cm/MHz的组织对超声信号传输效应的等效低通滤波和中心频率为8MHz、带宽分别等于2、4、6MHz的换能器发射超声信号的归一化幅频特性,fd7、fd8和fd9分别是带宽等于2、4、6MHz的换能器发射超声信号经过衰减系数为0.032Np/cm/MHz的组织散射以后中心频率的频移量。由fd7<fd8<fd9可知,换能器的带宽越宽,背散射信号的频移量越大。
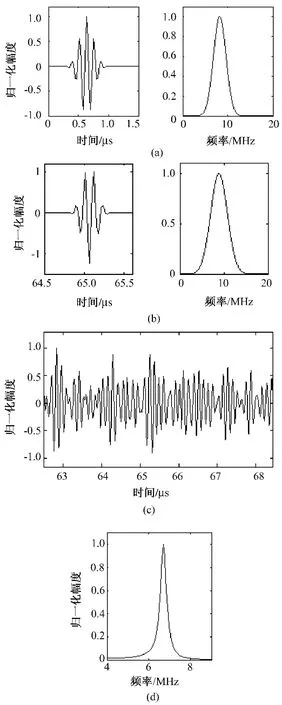
图2 发射脉冲、检测系统传输响应和背散射信号的模拟结果。(a)发射时域脉冲(左)及其归一化幅频特性(右);(b)检测系统传输响应(左)及其归一化幅频特性(右);(c)背散射信号时域图;(d)背散射信号的功率谱Fig.2 The simulation results of launch pulse,transmission response of detection system and backscattered signal.(a)launch pulse in time(left)and its normalized amplitude of frequency spectrum(right);(b)transmission response of detection system(left)and its normalized amplitude of frequency spectrum(right);(c)backscattered signal in time domain;(d)power spectrum of backscattered signal
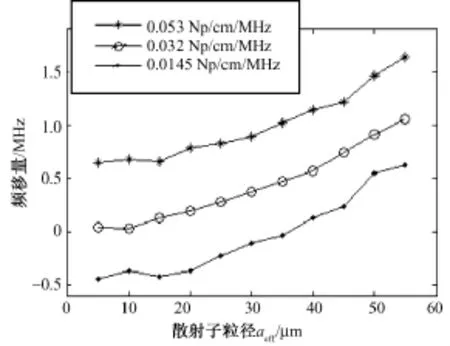
图3 不同衰减系数组织的背散射信号频移量随散射子粒径的变化Fig.3 The frequency offsets of backscattered signals from tissues versus scatterer size when tissues have different attenuation coefficients
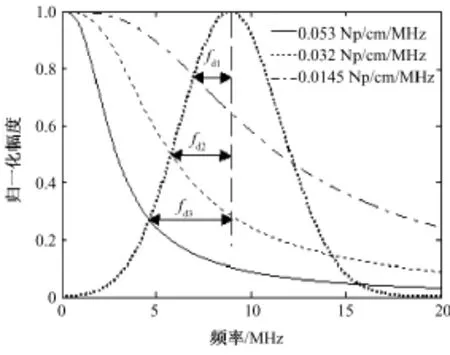
图4 不同衰减系数组织的背散射信号频移量比较(其中fd1、fd2和fd3分别是衰减系数为0.014 5、0.032、0.053Np/cm/MHz时的频移量)Fig.4 The comparison of frequency offsets of backscattered signals when tissues have different attenuation coefficients(fd1、fd2andfd3are the frequency offsets when attenuation coefficient is 0.014 5、0.032、0.053Np/cm/MHz,respectively)
由图5(c)可知,聚焦特性fN比较小时,背散射信号的频移量随散射子粒径的变化起伏比较大,二者的变化关系比较复杂;fN比较大时,背散射信号的频移量与散射子粒径接近线性关系。这可能是由于超声波衍射效应的影响,当聚焦特性fN比较小时,换能器的聚焦性比较强,衍射效应的影响显著,从而导致频移量起伏变化,当fN比较大时,换能器的发射声场接近平面波,超声波没有比较显著的衍射效应。
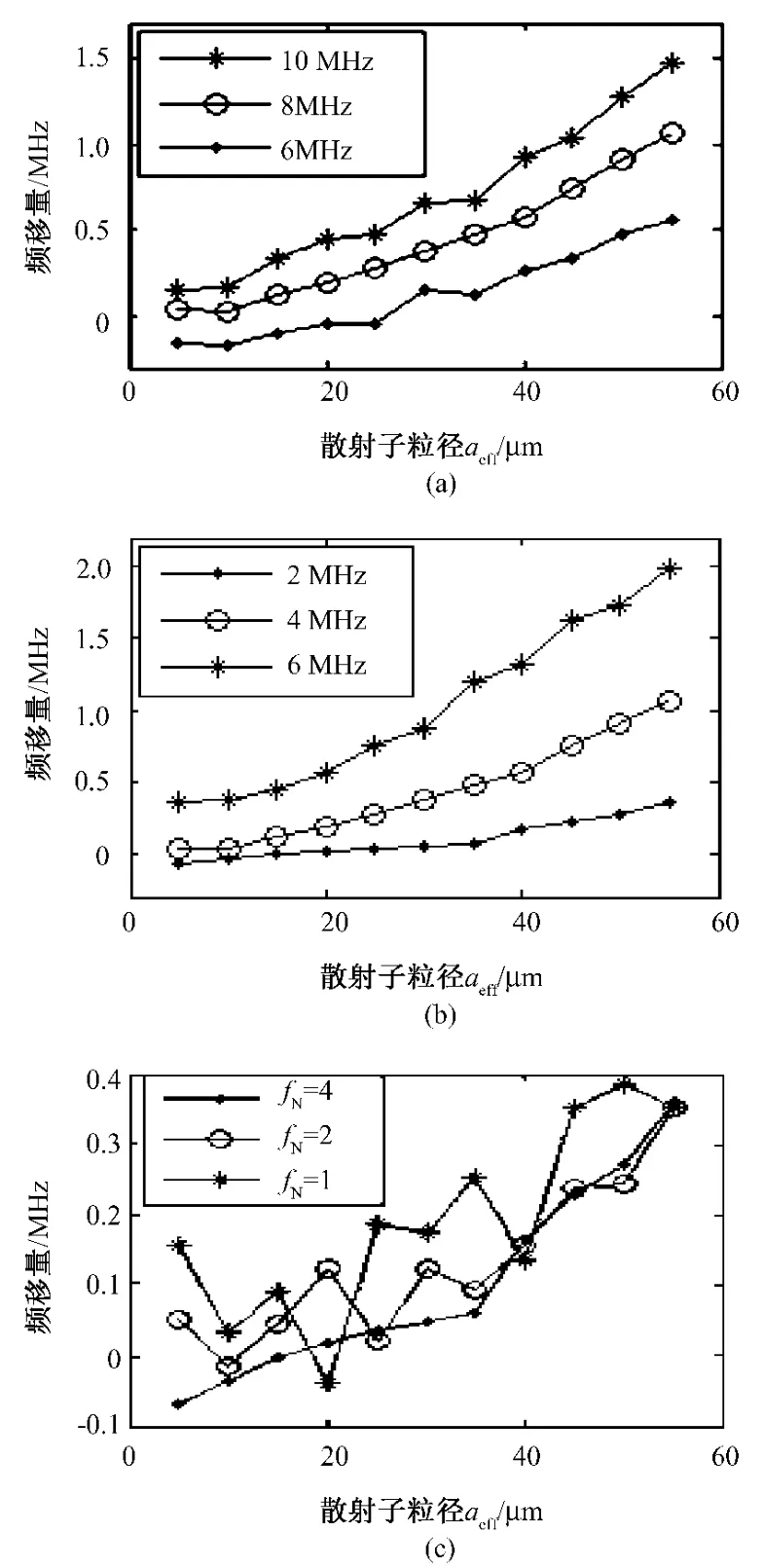
图5 发射换能器的参数不同时背散射信号的频移量随散射子粒径的变化。(a)不同中心频率;(b)不同带宽;(c)不同聚焦特性Fig.5 The frequency offsets of backscattered signals from tissues versus scatterer size when the launch transducer has different parameters.(a)different central frequencies;(b)different bandwidths;(c)different focal properties
3.3 散射子的数浓度对背散射信号频移量的影响图7是散射子的数浓度对背散射信号频移量的影响模拟结果。可以得出,在三种不同散射子数浓度的情况下,组织超声背散射信号中心频率的偏移量相接近。所以,背散射信号中心频率的偏移量不受散射子数浓度的影响。但在模拟过程中发现,不同散射子数浓度的情况下,背散射信号的功率谱幅度有变化,功率谱幅度随散射子数浓度的增大而增大。
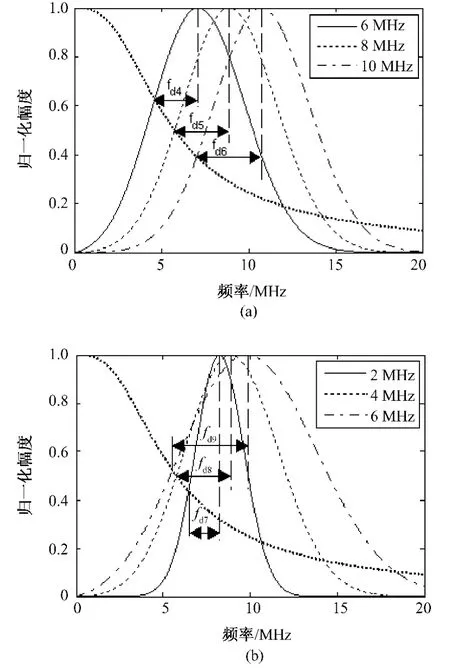
图6 发射换能器不同参数时背散射信号频移量的比较(其中,fd4、fd5和fd6分别是中心频率为6、8、10MHz时的频移量,fd7、fd8和fd9分别是带宽为2、4、6MHz时的频移量)。(a)不同中心频率;(b)不同带宽Fig.6 The comparison of frequency offsets of backscattered signals when launch transducer has different parameters(fd4、fd5andfd6are the frequency offsets when central frequency is 6、8、10MHz,respectively;fd7,fd8andfd9are the frequency offsets when bandwidth is 2、4、6MHz,respectively).(a)different central frequencies;(b)different bandwidths
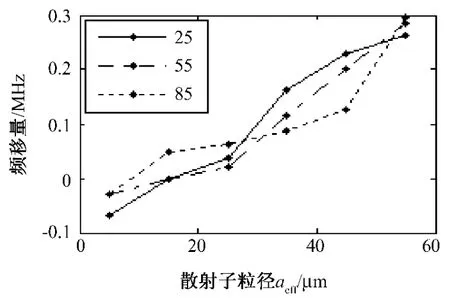
图7 散射子数浓度分别为25、55、85/mm3时,背散射信号的频移量随散射子粒径的变化Fig.7 The frequency offsets of backscattered signals versus scatterer size with concentration of scatterers is 25、55 and 85/mm3,respectively
4 讨论和结论
从生物软组织超声背散射信号的传输模型出发,以聚焦超声源的离散型散射模型为理论基础,假设入射信号和散射信号都为高斯型分布,通过理论分析和模拟实验,研究了聚焦超声换能器焦区内软组织超声背散射信号中心频率的偏移量与组织超声特征散射子粒径的相关性,分析了组织特性参数和换能器的参数对频移量的影响,利用超声背散射信号中心频率的偏移量估计软组织超声特征散射子的粒径等与频率有关的超声散射参数,探寻此项技术在生物软组织生理病理诊断中的应用。模拟结果表明:
1)超声换能器焦区内生物软组织超声背散射信号中心频率的偏移量随超声特征散射子粒径的增大而增加,近似呈线性增长的关系,中心频率随超声特征散射子粒径的增大而向低频方向移动。因此,聚焦超声换能器焦区内超声特征散射子粒径与中心频率的偏移量有一定的关联,这样就有可能通过超声特征散射子粒径参数的研究来表征软组织的生理病理特性。
2)频移量与组织的衰减系数、聚焦超声换能器的中心频率、带宽等有关,这些参数越大,频移量也越大。散射子的数密度、聚焦超声换能器的聚焦性等参数对频移量的影响不大。可见,不能只通过频移量来探讨软组织超声特征散射子的数密度进行组织定征,而且研究频移量时可以不考虑换能器的聚焦参数。
3)当生物软组织出现异常变化时,组织的衰减系数、弹性特性以及超声特征散射子的粒径和数浓度等都相应地会发生变化,软组织超声背散射射频信号中心频率的偏移量随之发生变化,可以综合考虑焦区特性、频移量等超声参量来对组织发生异常进行表征。
实验结果还表明,对于聚焦超声换能器,当聚焦性比较大时,超声波的衍射效应影响显著,使得超声诊断成像系统的分辨力和精确度变差;对于弱聚焦超声换能器,虽然没有超声波显著的衍射效应,但探头的横向分辨率比较差,也限制了超声诊断成像系统的分辨力和精确度;所以,在实际应用中,应该根据对分辨力和精确度以及穿透深度等方面的要求而选择换能器的聚焦性。
由于模型建立过程中用到了一些近似和假设条件,实际生物软组织及其变异组织对超声信号传输效应的差异规律仍然需要继续研究,需通过大量的临床统计实验,探讨正常与变异组织超声传输频移量的差异规律。
[1]Bigelow TA,O’Brien WD.Scatterer size estimation in pulse echo ultrasound using focused sources:Theoretical approximations and simulation analysis[J].J Acoust Soc Am,2004,116:578-593.
[2]Bigelow TA.Estimating the medical ultrasoundin vivopower spectrum[D].Illinois:University of Illinois at Urbana-Champaign,2004.
[3]Oelze ML,Zachary JF,O’Brien WD.Characterization of tissue microstructure using ultrasonic backscatter:theory and technique for optimization using a Gaussian form factor[J].J Acoust Soc Am,2001,112(3):1202-1211.
[4]Oelze ML,O’Brien WD.Method of improved scatterer size estimation and application to parametric imaging using ultrasound[J].J Acoust Soc Am,2002,112(6):3053-3063.
[5]Oelze ML,O’Brien WD,Blue JP,et al.Differentiation and characterization of rat mammary fibroadenomas and 4T1 mouse carcinomas using quantitative ultrasound imaging[J].IEEE Trans on Medical Imaging,2004,23(6):764-771.
[6]Ghoshal G,Oelze ML.Improved scatterer property estimates from ultrasound backscatter using gate-edge correction and a pseudowelch technique[J].IEEE Transactionson Ultrasonics,Ferroelectrics and Frequency Control,2010,57:2828-2832.
[7]Hafez ZT,Wirtzfeld LA,Battles A,et al.Estimating scatterer properties in rat fibroadenomas using various mathematical form factors[C]//Proceedings of the 2009 IEEE Ultrasonics Symposium.Rome:IEEE,2009:294-297.
[8]King MR,Anderson JJ,Herd M-T,et al.Ultrasonic backscatter coefficients for weakly scattering,agar spheres in agar phantoms[J].The Journal of the Acoustical Society of America,2010,128:903-908.
[9]陈启敏,郭建中.软组织深层超声回波信号解卷处理和提高分辨率的研究[J].中国生物医学工程学报,1999,18(2):130-137.
[10]Konofagou EE,Varghese T,Ophir J.Spectral estimators in elastography[J].Ultrasonics,2000,38:412-416.
[11]万明习.医学超声学[M].西安:西安交通大学出版社,1992:35-45.
[12]Quan Y,Harris JM.Seismic attenuation tomography using the frequency shift method[J].Geophysics,1997,62(3):895-905,410.
[13]他得安,王威琪,汪源源,等.评价松质骨状况的一种背散射频谱方法[J].声学技术,2007,26(3):406-410.
[14]Bigelow TA,O’Brien WD.“Scatterer size estimation in pulse echo ultrasound using focused sources:Calibration measurements and phantom experiments[J].J Acoust Soc Am,2004,116:594-602.
[15]Lyons ME,Parker KJ.Absorption and attenuation in soft tissues II-experimental results[J].IEEE Trans on Ultrasonics,Ferroelectrics and Frequency Control,1988,35(4):511-521.
[16]Parker KJ,Lyons ME.Absorption and attenuation in soft tissues I-Calibrations and error analysis[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1988,35(2):242-252.
[17]Goss SA,Frizzell LA,Dunn F.Ultrasonic absorption and attenuation in mammalian Tissues[J].Ultrasound Med & Biol,1979,5:181-186.

