基于解剖自适应的非局部先验贝叶斯PET图像重建

路利军 马建华 黄 静 毕一鸣 刘 楠 陈武凡

（南方医科大学 生物医学工程学院医学信息研究所，广州 510515）

引言

正电子发射成像（positron emission tomography，PET），是一种非介入的定量研究活体功能活度的临床工具。由于低空间分辨率和系统固有噪声，PET重建是一个病态问题［1］。统计图像重建方法，比如最大似然（maximum likelihood-expectation maximization，ML-EM），能够更好地考虑系统模型的物理效应，而且能够针对探测数据和噪声的统计特性建立数学模型，其迭代重建的图像质量要优于传统的以滤波反投影（filtered back projection，FBP）方法为代表的解析重建算法。然而，ML-EM方法在迭代过程中会伴随着图像质量退化而导致棋盘效应，从而导致非收敛的迭代过程［2］。此病态问题可以通过贝叶斯方法有效地求解［3-4］。基于贝叶斯理论，先验知识可以对原始的重建进行正则化，先验通常反映图像的局部平滑特性，然而在不同的解剖结构之间，放射性活度分布具有很大的变化，使得正则化先验很难满足图像的整体特性，所以如何有效地利用解剖组织和器官之间的放射性浓度变化，对于图像重建有重要的意义［5］。

常用的二次先验（quadratic membrane prior，QMP）是在一个局部邻域内，像素值的平均效应对重建图像起到正则化作用，在抑制噪声的同时，会对边缘细节产生过平滑效应［3］。为克服QMP的缺点，许多具有边缘保持作用的非二次先验，如Huber先验［6］，依据一个局部邻域内的像素灰度差，自适应决定对每个像素的正则化程度。然而，Huber先验会产生块状的平滑区域。与传统先验相比，在PET图像重建中引入高分辨率解剖信息的方法已有广泛研究［7-9］。然而，解剖图像并不能区分具有相同密度的正常组织和病变组织，几乎不能提供器官代谢活度信息，特别是病灶代谢活度信息，缺乏足够的信息来指导功能突变区域的重建［10］。所以，如何有效地利用不包含病灶边缘的解剖先验知识来指导PET图像重建，仍是一个具有挑战性的问题。

2005年，Buades和他的同事提出一种新的非局部均值（nonlocal means）滤波方法用于图像滤波［11-12］。基于非局部思想，一种非局部先验（nonlocal prior，NLP）被引入贝叶斯PET图像重建中［13］。非局部先验比传统局部先验，如二次先验和Huber先验，在图像噪声抑制和边缘保持方面具有更好的效果。然而，此先验对于参数h敏感，参数h控制相似性函数的衰减，通常设定为经验值，并且在迭代过程中对整幅图像只用一个参数。显然，一个固定的h来描述图像的边缘和结构特征是不准确的。由文献［11-12］可见，参数h是一个与噪声相关的量，然而对于低信噪比的PET图像，很难找到一种有效的噪声估计方法。基于PET图像的放射性活度在同一解剖区域是同质分布的，仅包含极少的由病灶引起的突变信号，通过引入解剖区域信息，可以在PET图像的每一个解剖区域有效地估计噪声。通过建立噪声与参数h的关系，非局部先验的参数h可以在每一个解剖区域自适应地达到最优，以保持重建图像边缘，并提高病灶对比度。实验证明，所提出的解剖自适应的非局部先验可以获得优质的PET图像。

1 方法与背景

1.1 PET统计模型

采用已广泛应用于发射计算机断层成像技术（包括PET和SPECT）的线性Poisson统计模型，即在探测数据服从Poisson分布的假设下，PET统计模型可描述为［15］

式中，yi为第i对探测器探测到的来自发射扫描的光子数据，N为探测器对的数目，fj为第j个重建像素点处的同位素分布，M为待重建图像像素的总个数，ri为在发射扫描中第i对探测器总共探测到的随机计数和散射计数，A=｛aij｝为系统矩阵，aij为为在理想条件下图像像素j被探测器对i探测到的几何概率。ci为扫描时间的校准系数、探测器的效率、衰减系数和死时间的校正系数的综合值。

PET重建的目标就是在已知测量数据y=［y1，y2，…，yN］T，系统矩阵A，c=［c1，c2，…，cN］T和r=［r1，r2，…，rN］T的情况下，重建出未知的同位素分布图像f=［f1，f2，…，fM］T，其中T表示矩阵的转置。

基于贝叶斯理论，由探测数据y得到PET图像f的最大后验估计，可以表示为

式中，P（y|f）是似然分布，P（f）是马尔可夫（MRF）先验分布。

常用的先验是吉伯斯（Gibbs）分布形式，有

式中，Z为正火常数或配分函数，U（f）为MRF先验能量，Uj（f）为图像f在像素点j处的能量函数值，β为控制MRF先验对于图像重建的影响程度。

求解式（2）的解f等同于求解使对数最大后验概率最大的的值，即

1.2 局部先验

传统上某像素点j处的Gibbs先验能量方程Uj（f），通常是该像素点与其邻域Nj内逐点差分为自变量的势能函数v（·）的简单加权和，即

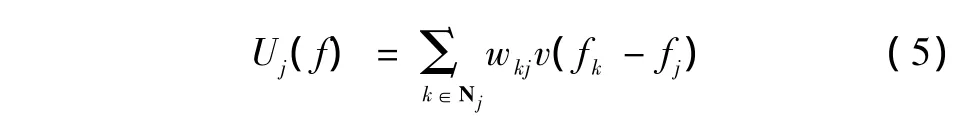
式中，权值量wkj为表征图像中像素点k和j间相互关系的正常数。一般设定wkj与像素点k、j之间的距离Dkj成反比。

通常，势能函数v的不同设计将直接导出不同的先验。当选择v（t）=t2/2时，则先验为QMP；当选择时，则为Huber先验，δ为参数。

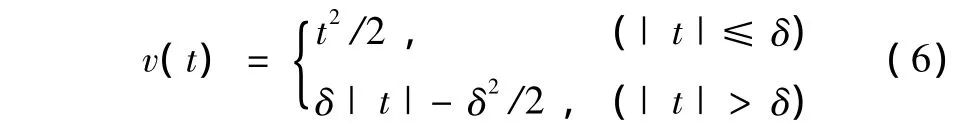
1.3 解剖先验

一个基本的假设是：PET图像的放射性活度分布在一个给定的解剖区域内是平滑的，只在不同组织结构之间会有明显的边缘。在此基础上，解剖先验被引入统计迭代重建过程中，用来指导PET图像重建。最常用的方法就是通过解剖边缘信息来计算二次先验的权值，记为AMAP［7，16］。式（5）中的权值量wkj，对于像素k和j属于不同的解剖区域，wkj=0；对于像素k和j属于相同的解剖区域，wkj=1/Dkj。这样，在不同解剖区域之间，平滑先验不做惩罚，可以有效地保持不同器官边缘的代谢浓度突变。

1.4 解剖自适应的非局部先验

基于非局部均值图像去噪，一种非局部先验已被用于贝叶斯PET图像重建［13］，定义为

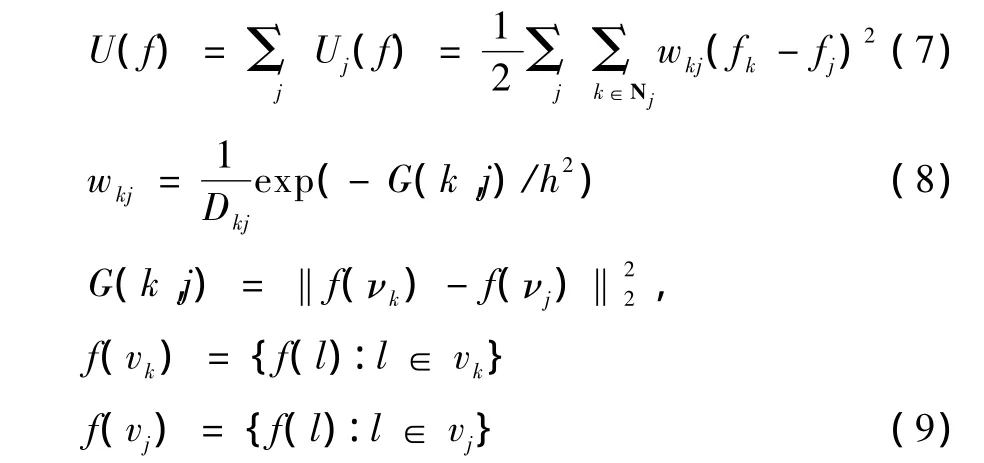
式中，Nj为以像素点j为中心的搜索邻域；wkj用于刻画像素k和j之间的相似性测度，用分别以像素k和j为中心的相似邻域vk和vj间的相似性函数计算。G（k，j）表示两相似邻域vk和vj间的L2距离，参数h控制相似性函数的衰减。

式（8）中参数h对权值量wkj的计算是极为重要的，在非局部先验中，参数h通常设定为经验值。显然，对于PET图像重建在整个迭代过程中只用一个参数h是有问题的。由文献［11-12］可知，参数h是一个与噪声相关的量，然而对于低信噪比的PET图像，很难对于整幅图像进行噪声估计。根据文献［14］，由于放射性浓度在单一的解剖区域是局部平滑，并且图像的结构不会发生大的变化，所以在每一个解剖区域的噪声标准差可以根据像素值的局部统计特性计算。因此，将解剖图像的区域信息引入PET图像中，提出参数h估计方法，有

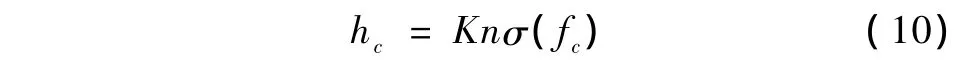
式中，c表示PET图像f中解剖区域的类型，hc表示图像f中区域c的h值，n表示相似邻域vk和vj的大小，σ（fc）表示图像f中区域c的噪声标准差，K为一个尺度参数。

由于PET图像的放射性浓度在不同解剖区域之间会有明显变化，因此将所提出的解剖自适应的非局部权值定义为

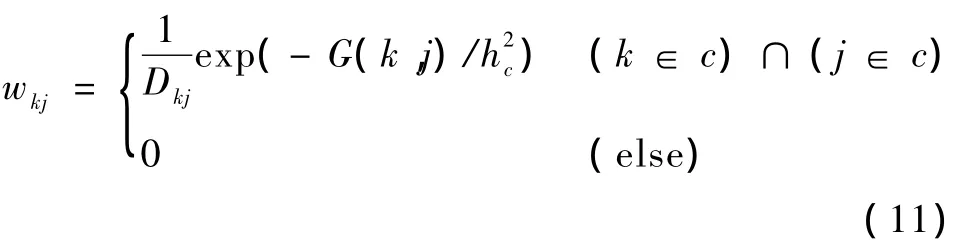
式中，如果像素k和j属于同一解剖区域，权值量wkj分别用以像素k和j为中心的相似邻域vk和vj间的相似性函数计算；如果像素k和j不属于同一解剖区域，则权值量wkj为0。通过实验发现：当hc远小于nσ（fc）时，不能有效地抑制图像噪声；当hc等于nσ（fc）时，会对重建图像产生过平滑效应。在实验中，选择K=0.5，选取FBP重建结果作为所有重建的初始值，期望随着每一步迭代正则化的作用，对每一个解剖区域c，图像标准差σ（fc）减小，h由一个初始值收敛到一个常数值。

2 两步式联合估计重建策略

步骤1：参数hc和权值量wkj更新，有

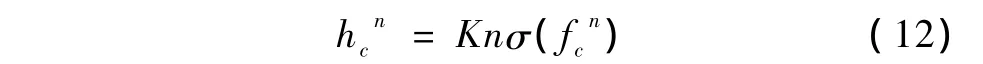
式中，hcn为图像f中区域c在第n步迭代中的h值，σ（fcn）为图像f中区域c在第n步迭代中的噪声标准差。

将与区域和迭代步数相关的hcn代入式（11），基于式（9）～式（11）计算wkj。

步骤2：图像更新。

固定步骤1得到的wkj后，经（4）式最大化计算得到重建图像f，可以采用抛物线替代坐标上升（paraboloidal surrogate coordinate ascent，PSCA）算法［17］进行迭代求解。PSCA算法可以看作OSL（one step late，OSL）算法的一种，其基本思想是将复杂的统计重建优化问题转化为易于求解的优化问题，具有收敛速度快、易于应用的特点。算法的收敛性难以给出严格的证明［2］，但在整个迭代过程中至少可以收敛到某局部最优值。

3 仿真实验

3.1 仿真Zubal体模实验

PET图像采用大小为128像素×128像素的改进Zubal体模，如图1（a）所示。软组织和肺区的衰减系数分别为0.095cm-1和0.03cm-1［18］。设计3个大小3像素×3像素的病灶：病灶1和3都在软组织区域内，病灶3靠近边缘，病灶1位于软组织区域中，病灶2位于左肺区。黄线划定7像素×7像素的区域，分别表示肺区和软组织区的背景。解剖图像采用不带病灶的Zubal体模，像素取值为0～0.095，如图1（b）所示。从图中可以看出，在解剖图像中并没有与功能图像相应的病灶边缘。病灶、软组织、肺区的相对活度比为4∶2∶1，像素取值范围为0～8。PET探测数据模拟中，光子总计数为9×105，探测数据服从泊松分布，其中模拟延迟随机计数ri占总计数的10％（忽略散射作用），同时设定校正系数ci为服从标准差等于0.3的log-normal随机变量。转换概率矩阵A对应于一个平行带状积分的几何模型，此二维模型表示一个180°的均匀区域里、有128个径向取样和128个角采样的系统，由Fessler等人提供的ASPIRE软件系统生成［19］，所有程序均在Intel（R）Pentium（R）4 2.80GHz双核处理器、2GB内存的PC机上实现。

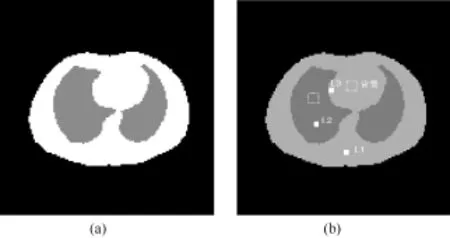
图1 仿真体模。（a）改进的Zubal体模（软组织中白线圈定的区域作为病灶1和病灶3的背景，肺区中白线圈定的区域作为病灶2的背景）；（b）用于AMAP和AANLP重建的解剖先验Fig.1 Simulated phantom.（a）modified Zubal phantom（The region defined by the white dotted line in the soft tissue is as the background region of lesion 1 and lesion 3，while the region in lung is used for lesion 2）；（b）the anatomical prior used in reconstructions with AMAP and AANL prior

3.2 图像重建及评价

采用基于QMP、Huber、NLP和AANLP的MAP算法，对探测数据进行重建。为评价重建过程中解剖边缘信息的作用，还采用AMAP进行重建。为加快收敛，所有重建算法都采用FBP重建结果作为初值，迭代步数选取150步。采用归一化均方根误差（normalized root mean square error，NRMSE）作为偏差的度量，采用归一化的标准差（normalized standard deviation，NSD）作为噪声的度量，则NRMSE定义为

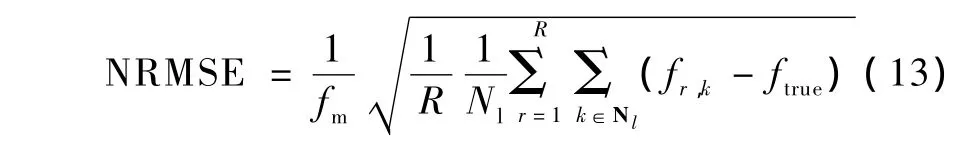
式中，ftrue为体模图像中感兴趣区域的真实像素值，fm为ftrue的均值，Nl是感兴趣区域的像素个数，R为随机数据的数目，fr，k为第r次随机数据中第k个像素值，则NSD定义为

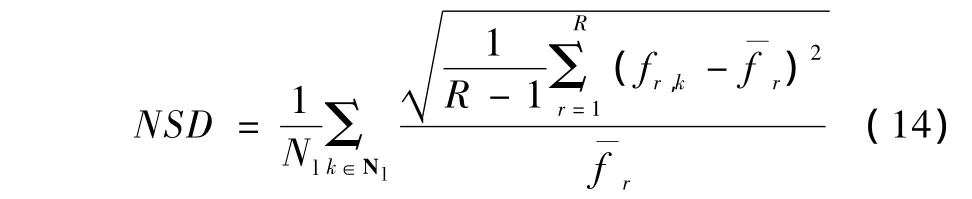
式中，fr，k的r和k定义与式（13）相同，r为像素k在r次重建中的均值。

为量化评价重建PET图像中病灶和正常背景区域对比度恢复水平，计算对比度恢复比（contrast recovery ratio，CRR）。R次随机数据重建的平均对比度定义为

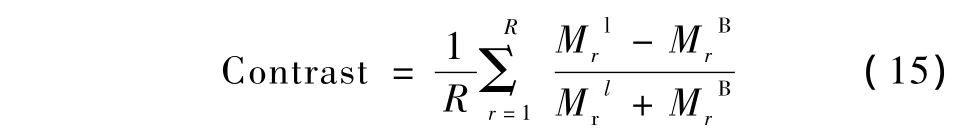
式中，Mrl与MrB分别为在r次随机数据中病灶l与背景B的平均灰度值。

CRR通过重建图像与体模图像对比度的比值计算。

4 结果

图2为对Zubal体模的重建图像。对于所有重建，设定β=1.5；对于NLP重建和AANLP重建，Nj设定为11像素×11像素，vk和vj设定为7像素×7像素。图2（a）为FBP重建，含有大量噪声。在图2中（b）～（d）分别对应于QMP重建、AMAP重建和Huber先验重建，（e）～（g）分别为对应于一个固定的β选取不同的h值进行NLP重建。图2（h）为AANLP重建，可以有效地保持病灶边缘结构。与其他方法相比，提出的方法具有更好的视觉效果。

在AANLP重建中，对于不同的β值，可得到参数h随迭代次数的函数，见图3。可以看到，对于不同的惩罚参数β，h收敛到不同的值，惩罚参数β与参数h成反向关系。这是由于随惩罚参数增大，每一步迭代中的正则化对图像影响较大，图像噪声可以得到有效抑制。比较图3中的（a）和（b）可以看到，对于相同的惩罚参数β，在不同的解剖区域，参数h收敛到不同的值。

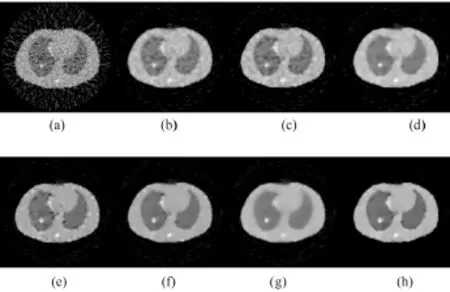
图2 重建图像。（a）FBP重建；（b）QMP重建；（c）AMAP重建；（d）Huber重建，δ=0.2；（e）NLP重建，h=0.8；（f）NLP重建，h=1.2；（g）NLP重建，h=2；（h）AANLP重建Fig.2 Reconstructed images.（a）FBP；（b）QMP Re；（c）AMAP Re；（d）Huber Re，δ=0.2；（e）NLP Re，h=0.8；（f）NLP Re，h=1.2；（g）NLP Re，h=2；（h）AANLP Re

图4描绘出病灶NRMSE与背景NRMSE的曲线：30次随机模拟数据，β取值区间为［0.01，0.1，0.2，0.5，1.0，1.5］；在NLP重建与AANLP重建中，Nj设定为11像素×11像素，vk和vj设定为7×7。对于病灶1和病灶2，QMP重建和AMAP重建有相似的表现；对于病灶3，AMAP重建由于利用了解剖边缘信息，比QMP重建具有更小的NRMSE。整体来说，Huber重建要优于QMP重建和AMAP重建。从图4中可以看到，NLP重建当h=0.8时，惩罚参数β调整，对重建结果影响不大；当h在1.2～1.6之间时，可以达到最低的病灶NRMSE与背景NRMSE；而当h＞1.6以后，随着β增大，在抑制背景噪声的同时，病灶NRMSE也急剧上升。在AANLP重建中，其曲线特性近似于NLP重建中h=1.2时的曲线特性，在病灶NRMSE方面更具鲁棒性，较NLP重建，QMP重建和AMAP重建可以取得更小的病灶NRMSE与背景NRMSE。

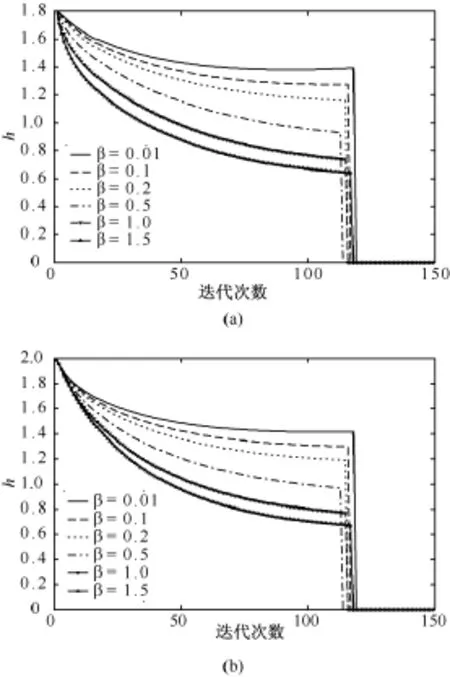
图3 AANLP重建中，对于不同的β值，参数h在不同区域随迭代次数的函数。（a）肺区；（b）软组织区Fig.3 The automatically estimated parameterh from AANLP reconstruction isplotted asa function of iteration for differentβvalue in different regions.（a）lung region；（b）soft tissue region

图5描绘出病灶CRR与背景NSD的曲线：30次随机模拟数据，β取值区间为［0.01，0.1，0.2，0.5，1.0，1.5］；在NLP重建与AANLP重建中，Nj设定为11像素×11像素，vk和vj设定为7像素×7像素。对于病灶1和病灶2，由图5（a）可以看到，QMP重建和AMAP重建在整个惩罚参数β范围内有相似的表现；对于病灶3，由图5（c）可以看到，当惩罚参数β逐渐增大到正常范围时，AMAP重建比QMP重建具有更高的病灶CRR。同时可以看到，Huber重建在整体上要优于QMP重建和AMAP重建。从图5（a）（c）可以看到，对于低对比度的病灶1和病灶3，NLP重建中当h=0.8时，并不能有效地抑制噪声，惩罚参数β调整，对重建结果影响不大；当h在1.2～1.6之间时，可以稳定地得到较大的病灶CRR，同时能有效地抑制背景区域的噪声；而当h＞1.6以后，随着β增大，在抑制噪声的同时，病灶CRR也急剧下降。在AANLP重建中，其曲线特性近似于NLP重建中h=1.2时的曲线特性，在病灶背景对比度方面更具鲁棒性。同时，可以从图5（c）看到，在AANLP重建中，病灶3的CRR要略优于NLP重建中病灶3的CRR，这是由于病灶3的边缘正好与解剖边缘重合，AANLP重建利用了解剖边缘。对于高对比度的病灶2，不同参数的NLP重建和AANLP重建具有相似的曲线特性。所以，笔者提出的AANLP重建较NLP重建，在病灶CRR方面具有更好的鲁棒性；较QMP重建，AMAP重建和Huber重建有更高的病灶背景对比度。

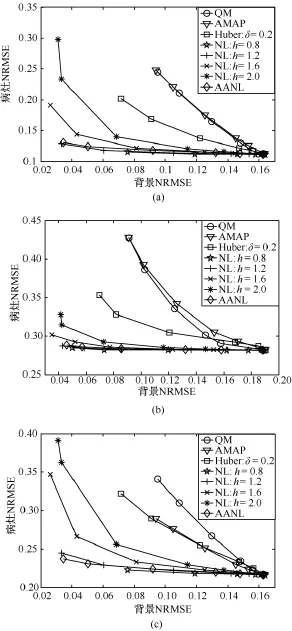
图4 病灶NRMSE与背景NRMSE的曲线。（a）病灶1；（b）病灶2；（c）病灶3Fig.4 The NEMSE of lesion versus the NRMSE of the background for all the reconstruction algorithms.（a）Lesion 1，（b）Lesion 2，（c）Lesion 3

5 讨论和结论

本研究提出了一种解剖自适应的非局部先验，将解剖信息引入到图像重建中。解剖信息的利用包含两个方面：一是解剖图像的边缘信息用来指导PET图像在边缘处的放射性活度值，二是解剖图像的区域信息用来估计非局部先验在每一个区域的参数h值。图像重建采用两步式联合估计：首先，对当前PET图像的每一个解剖区域，根据局部统计特性自适应的估计参数h，计算非局部先验权值；然后，进行图像更新。实验表明，本研究提出的AANLP重建，可以得到较NLP重建更优的结果。

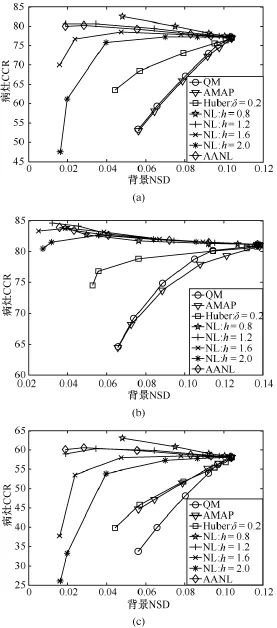
图5 病灶CCR与背景NSD的曲线。（a）病灶1；（b）病灶2；（c）病灶3Fig.5 The CCR of lesion versus the NSD of the background for all the reconstruction algorithms.（a）Lesion 1；（b）Lesion 2；（c）Lesion 3

在本研究中，所提出的AANLP重建算法亦可以看做是OSL算法的一种形式，其算法的收敛性难以给出严格的证明，所以并不能保证收敛到一个全局最大值。但是可以看到，算法至少可以收敛到一个局部极大值，AANLP重建可以很好地抑制背景噪声，保持边缘，并且具有最高的病灶背景对比度。提出的参数h估计方法，除参数K外，还与相似性计算窗宽有关；对于不同相似性计算窗宽进行实验，得到病灶NRMSE与背景NRMSE的曲线。实验表明，所提出的方法在不同的窗下均可以有效地自适应估计参数h。存在的问题是研究基于一个基本的假设，即放射性活度在同一解剖区域是同质分布的，且实际的解剖结构会远比仿真的Zubal体模复杂。对于PET图像，某些解剖区域内放射性活度是异质分布的，在解剖区域内的标准差估计会有偏差，从而引起参数h的偏差。所以，找到一种更有效的PET图像标准差估计方法是今后研究的重点。对于解剖结构较为复杂的CT图像，准确的分割方法也是本方法应用的关键。另外，进一步的研究工作包括对本方法进行临床数据的评价。

［1］Rahmim A，Zaidi H.PET versus SPECT：strengths，limitations and challenges［J］.Nucl Med Commun，2008，29（3）：193-207.

［2］Lange K.Convergence of EM image reconstruction algorithms with Gibbs smoothness［J］.IEEE Trans Med Imaging，1990，9（4）：439-446.

［3］Geman S，Geman D.Stochastic relaxation，Gibbs distribution，and the Bayesian restoration of images［J］.IEEE Trans Patt Analy and Mach Intell，1984，26（2）：721-741.

［4］Li SZ.Markov Random Field Modeling in Image Analysis［M］.Tokyo：Springer-Verlag，2001.

［5］Gindi G，Lee M，Rangarajan A，et al.Bayesian reconstruction of functional images using anatomical information as priors［J］.IEEE Trans Med Imaging，1993，12（4）：670-680.

［6］Chlewicki W，Hermansen F，Hansen SB，et al.Noise reduction and convergence of Bayesian algorithms with blobs based on the Huber function and median root prior［J］.Phys Med Biol，2004，49（20）：4717-4730.

［7］Comtat C，Kinahan PE，Fessler JA，et al.Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels［J］.Phys Med Biol，2002，47（1）：1-20.

［8］Bowsher JE，Johnson VE Turkington TG，et al.Bayesian reconstruction and use of anatomical a priori information for emission tomography［J］.IEEE Trans Med Imaging，1996，15（5）：673-686.

［9］Bruyant PP，Gifford HC Gindi G，et al.Numerical observer study of MAP-OSEM regularization methods with anatomical priors for lesion detection in/sup 67/Ga images［J］.IEEE Trans Nucl Sci，2004，51（1）：193-197.

［10］Vogel WV，Oyen WJ，Barentsz JO，et al.PET/CT：Panacea，redundancy，or something in between?［J］.J Nucl Med，2004，45（1 suppl 1）：15S-24S.

［11］Buades A，Coll B and Morel JM.A non-local algorithm for image denoising［C］//Proceedings of IEEE Comp Vis and Pattern Rec.San Diego：IEEE，2005，2：60-65.

［12］Buades A，Coll B，Morel JM.A review of image denoising algorithms，with a new one［J］.Multiscale Model Simul，2006，4（2）：490-530.

［13］Chen Yang，Ma Jianhua，Feng Qianjin，et al.Nonlocal prior Bayesian tomographic reconstruction［J］.J Math Imaging Vis，2008，30（2）：133-146.

［14］Chan C，Fulton R，FengDD，etal.Regularized imge reconstruction with an anatomically adaptive prior for positron emission tomography［J］.Phys Med Biol，2009，54（24）：7379-7400.

［15］Sheep LA，Vardi Y.Maximum likehood reconstruction for emission tomography［J］.IEEE Trans Med Imaging，1982，1（2）：113-122.

［16］LipinskiB，Herzog H，Rota KE，et al.Expectation maximization reconstruction of positron emission tomography images using anatomical magnetic resonance information［J］.IEEE Trans Med Imaging，1997，16（2）：129-136.

［17］Fessler JA，Erdogan H.A paraboloidal surrogates algorithm for convergent penalized-likelihood emission reconstruction［C］//In Proceedings of IEEE Nuc Sci Symp.Toronto：IEEE，1998，2：1132-1135.

［18］Meikle SR，Hutton BF，Bailey DL，et al.Accelerated EM reconstruction in total-body PET：potential for improving tumor detestability［J］.Phys Med Biol，1994，39（10）：1689-1704.

［19］Fessler JA.Aspire 3.0 user’s guide：A sparse reconstruction library［R］.Communication＆ Signal Processing Laboratory Technical Report No.293，1998.