基于邻域信息和高斯加权卡方距离的脊椎MR图像分割

郑 倩 卢振泰* 陈 超 冯前进 陈武凡*（南方医科大学医学图像处理重点实验室，广州 5055）（南方医科大学中医药学院外科骨科教研室，广州 5055）

引言

随着社会老龄化和工作压力日益增大，各种脊椎疾病（如椎间盘退化、椎间盘突出、椎管狭窄症等）困扰着各个年龄段和各种职业的人群，成为影响公共健康的几大顽疾之一。脊椎的毗邻结构上下交错，外科医生需要具有良好的方位感，精确地知道椎体的形状，因为对椎体的形状识别是提高手术精度、降低手术风险的关键一步。图像分割是提取图像中特殊组织的定量信息所不可缺少的手段，也是可视化实现的预处理步骤和前提［1］。分割后的图像被广泛用于三维重建、图像配准、组织容积的定量分析和计算机辅助手术导航系统等方面。

描述人体脊椎生理解剖结构的常见成像方式有计算机断层扫描（CT）和磁共振成像（MRI）。CT密度分辨率高，骨骼、皮肤等不同类型组织之间的灰度差异较大，用区域生长法可以很好地分割出脊椎CT图像中的椎体。MRI因软组织对比度变化和射频场非均匀性等因素的影响，增加了分割出椎体的难度。

传统的分割算法往往陷入非全局最优而导致分割结果比较差，如水平集方法［2］、活动轮廓方法［3］、K-均值（K-means）算法等［4］。基于图论的图像分割技术是一种新的图像分割技术，是一种无监督图像分割技术，不需要初始化。该方法将图像映射为带权无向图，将图像分割问题转换为图的最优划分问题；它利用剪切准则得到图像的最佳分割，是一个全局准则，得到的是全局最优解。该分割技术也是一种点对聚类方法，近年来在国际上的图像分割领域和数据聚类中表现出了良好前景。Julio等提出了基于归一化割（normalized cuts）的MRI椎体分割技术［5］，利用了一种概率统计特征——局部灰度直方图，需要反复实验调节一个合适的尺度参数，只能处理T1加权图像；由于没有利用邻域的空间信息，分割精度不高，甚至会因图像中椎体与周围组织的对比度不高而使分割结果偏差极大。

由于成像技术存在噪声和各向异性因素的影响，图像中同一解剖组织结构的像素点灰度值会发生很大变化，仅用单个像素灰度值这一特征并不能准确描述一幅图像，因此利用邻域灰度信息这个特征来描述一幅图像，从而引入了图像的空间结构信息。在此特征基础上，提出了一种新的相似度矩阵构造方法——基于邻域信息和高斯加权的卡方距离，并利用Zelnik等提出的局部收缩方法来自适应地调整尺度参数［6］，实现二维椎体的准确分割。即使在有噪声影响的情况下，该算法也能够快速、准确地分割出椎体，对于正常及病变椎体，所提出的算法分割出的椎体轮廓都光滑、清晰。作为一种一般性的分割方法，该算法可以拓展到其他器官的分割中。

1 基本理论

1.1 图论的基本理论

基于图论的图像分割方法的基本原理如下：对于一幅输入的图像或一个特征点集，建立一个带权的无向图G=（V，E），其中节点vi∈V表示图像像素，边（vi，vj）∈E连接节点vi和vj。每条边有一个相应的非负权重ω（vi，vj），表示相邻节点vi和vj的相似程度。在图像分割中，边的权重表示两个像素间的近似关系，如灰度、颜色、位置或其他局部分布的差别。然后，在所建立的图上利用割集准则对图中的节点进行划分，进而完成对图像的分割。

割集准则直接影响到分割结果的优劣，最早提出的割集准则是最小割集准则（minimum cut）［7］。将图像映射的无向图的节点分割为互不相交的k个部分A1，…，Ak，且A1∪…∪Ak=V，则切的代价函数为

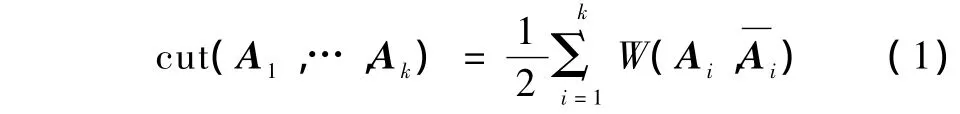
Shi等提出了归一化割算法［8］，同时利用归一化割集准则，实现对原图像的分割。归一化割集准则不仅使子图之间的相似度最小，而且令划分成的各个子图（区域）的内部相似度最大，同时避免了划分的区域出现歪斜（即偏向小区域）分割。切的代价函数为

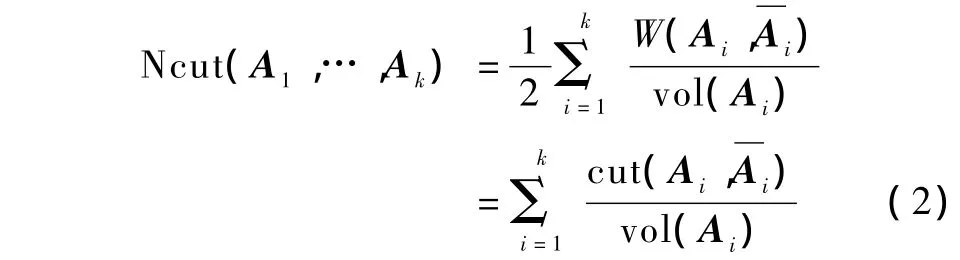
Ng等提出了NJW算法［9］，该算法和Normalized cuts一样，都是基于归一化分割准则，其唯一的不同是构造的拉普拉斯矩阵为L=D-1/2WD-1/2，克服了Shi算法在各个簇的簇内总度数assoc（Ai）=vol（Ai）-cut（Ai，i）差别大时效果不理想的缺点，稳定性更好，是最常用的谱分割算法之一。

2 基于邻域信息和高斯加权卡方距离的脊椎MRI分割

在基于图论的图像分割中，最重要的是构造相似度矩阵，即如何度量两点之间的距离并选择合适的尺度参数。本研究首次将NJW算法用到脊椎MRI图像分割中，并且在算法中构造了一种新的相似度矩阵——基于邻域信息的高斯加权卡方距离，同时引入局部收缩思想，提高椎体分割的准确性。

2.1 构造相似度矩阵

2.1.1 基于邻域信息和高斯加权的卡方距离

在基于图论的分割算法中，如何构造相似性矩阵是一个研究热点。NJW算法构造相似度矩阵时，仅仅考虑了单个像素的灰度值，如果同一组织结构上像素灰度值变化大或器官周围灰度值相近，就会导致错误的聚类和分割结果。因此，引入图像的结构特征，用邻域内所有像素的灰度值来代替单个像素的灰度值，利用高斯函数进行加权。图像中两个节点（像素点）vi和vj之间的卡方距离表示为

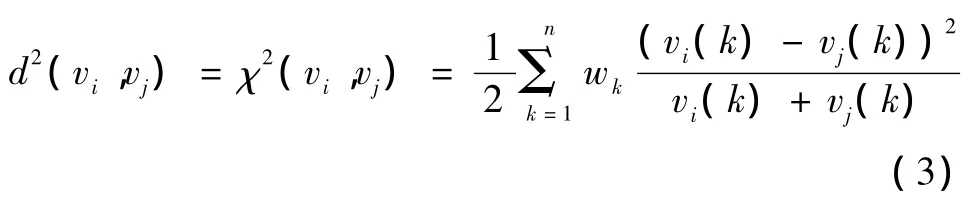
式中，vi（k）表示某节点5像素×5像素邻域内第k个像素点的灰度值，wk是特征权重。特征权重wk根据一定的先验信息赋值，离该节点距离较近的像素特征权重较大；相反，离该节点距离较远的像素特征权重较小。利用高斯核函数分别为该像素邻域内的25个像素赋予特征权重，从而将邻域信息融合在一起，更好地描述了两个像素点的相似性。

2.1.2 局部收缩

NJW算法在构造相似性矩阵时，需要一个尺度参数σ，以来控制两个样本点vi和vj之间的距离对相似度矩阵W的影响，从而构造出合适的相似度矩阵，提高聚类的性能和分割结果的准确性，而算法是根据K-means的聚类效果（即能否给出最紧凑的聚类）来决定合适的尺度参数的。因此，在找到合适的参数前，必须反复地进行特征值分解和K-means的迭代，且需要人工调整才能最终收敛到最优解。由此可见，该算法具有局限性，且计算量比较大。

局部收缩并不是为整个样本集选择一个尺度参数σ，而是为每一个样本点vi选择一个σi，将样本点vi到vj的距离表示为d（vi，vj）/σi。其中，σi=d（vi，vK），vK是样本点vi的第K个近邻。在实验中，一般选取K=7，这是一个经验值，因为此时算法的聚类效果最佳。

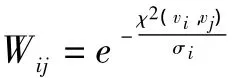
2.2 分割方法

在研究中，分割方法对所有实验的所用图像进行了各向异性的扩散滤波。在构造新的相似度矩阵的基础上，提出了基于图论的归一化分割优化准则的二维椎体分割算法，结合数学形态学，实现了椎体二维（2D）分割及显示。本方法在实现过程中，聚类数C=35（在分割其他的器官时，可做相应调整），需要人工用鼠标选择要显示的椎体，其中的参数不需要调节，就可以得到准确的分割结果。

本算法流程如图1所示，包括7个步骤。

步骤1：在2D MRI脊椎的图像上，由手工点选需要显示的椎体；

步骤2：对图像进行各向异性扩散滤波［10］；

步骤3：利用2.1中的方法，构造相似度矩阵；

步骤4：计算NJW算法中提出的拉普拉斯矩阵；

步骤5：找到拉普拉斯矩阵最大的C个特征值；

步骤6：对前C个特征向量用K-means进行聚类，得到图像的聚类结果；

步骤7：用数学形态学修整分割椎体的边缘，得到分割后椎体图像和椎体边缘图像。

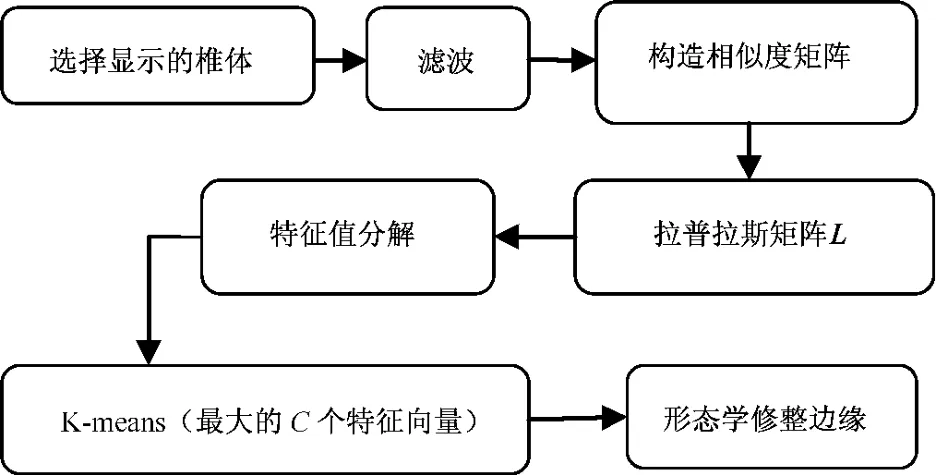
图1 算法流程Fig.1 Block diagram for the proposed algorithm

3 实验方法

实验数据为4组有代表性的2D矢状面T1加权和T2加权MR图像，大小为512像素×512像素。为了验证算法的有效性和可行性，将该算法和传统的NJW算法［9］做了定性分析。临床专家的手动分割结果作为金标准，定量地分析本算法的精确性。计算像素重叠数，即手工分割和本研究自动分割算法的交集；假阴性像素个数，即被自动分割方法遗漏的椎体像素数；假阳性像素个数，即自动分割方法错误划分为椎体的像素数；覆盖率，即像素重叠数除以自动分割像素数，并将其作为评价标准。由于NJW算法在选择合适的尺度参数时需要反复实验，而本算法只需要一次实验，具有明显的优势，故不对比算法执行时间。作为一种一般性的分割方法，本算法还可拓展到其他器官的分割中，用了3组MR脑肿瘤数据进行实验验证。

实验硬件环境为处理器Intel Core Duo（2.53GHz）、内存2GB，软件环境为Windows 7操作系统，所用工具软件为Matlab2008a和Visual Studio 2008。

4 结果

4.1 实验1

患者椎体正常，椎体毗邻组织与椎体灰度相近（T1加权图像）。

NJW算法：用每个像素的特征值（本实验中采用灰度值）且不用局部收缩来进行脊椎MRI的椎体自动分割实验，实验结果如图2（a）所示，白色实线是分割椎体的轮廓。从实验结果可知，在椎体和毗邻组织接触处灰度相近，造成了过分割现象（如图2（a）黑色箭头所示）；而在分割其他椎体时，出现欠分割现象（如图2（a）白色箭头所示）。

本算法：考虑像素点的邻域信息，利用高斯函数，对该5像素×5像素邻域内像素点的25个灰度值进行加权，结合局部收缩进行脊椎MR图像的椎体自动分割实验，结果如图2（b）所示，白色实线是分割椎体的轮廓。即使在灰度值相近的区域，该算法也能准确的分割出椎体，光滑且清晰，克服了NJW算法中的过分割和欠分割现象，分割椎体轮廓和椎体形状较为接近。

手动分割算法：图2（c）为临床专家手动分割脊椎MRI的椎体实验结果，白色实线是分割椎体轮廓。手动分割结果作为金标准，验证本研究改进算法分割椎体的准确性和有效性。从表1可知，本算法和手动分割算法较为接近。

4.2 实验2

患者椎体正常，椎体周围毗邻组织与椎体灰度差异较大（T2加权图像）。

脊椎MRI图像中，患者椎体未发生形变，椎体周围毗邻组织与椎体差异较大，这类脊椎MRI图像较容易分割，实验结果如图3所示。NJW算法有一定的过分割现象（如图3（a）黑色箭头所示），而本算法能准确分割出椎体，光滑且清晰，克服了NJW算法中的过分割现象，分割椎体轮廓和椎体形状较为接近。从表1可知，本算法和手动分割算法较为接近。

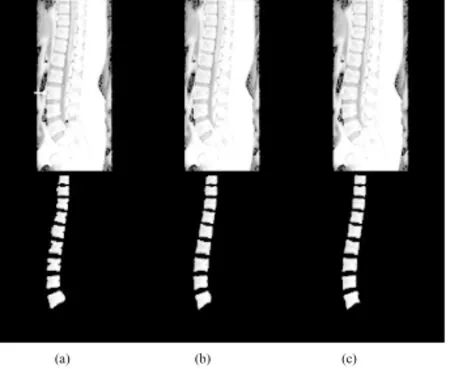
图2 分割的椎体轮廓（上）和分割的椎体（下）。（a）NJW算法；（b）本算法；（c）手动分割Fig.2 The contours（upper）and the segmentations of the vertebral bodies（bottom）.（a）NJW algorithm；（b）the proposed algorithm；（c）manual segmentation

图3 分割的椎体轮廓（上）和分割的椎体（下）。（a）NJW算法；（b）本算法；（c）手动分割Fig.3 The contours（upper）and the segmentations of the vertebral bodies（bottom）.（a）NJW algorithm；（b）the proposed algorithm；（c）manual segmentation

4.3 实验3

患者椎体正常，扫描到一块椎体的椎弓根（T2加权图像）。

患者的椎体正常，由于患者扫描位置的不同，该类矢状面MRI图像不仅扫描到了椎体，其棘突等与椎体连接的部分也被扫描到（如图4（a）中黑色箭头所示）。NJW算法不能把棘突分割出来，而本算法能准确分割出椎体，光滑且清晰，克服了NJW算法中的欠分割现象，分割椎体轮廓和椎体形状较为接近。从表1可知，本算法和手动分割算法较为接近。

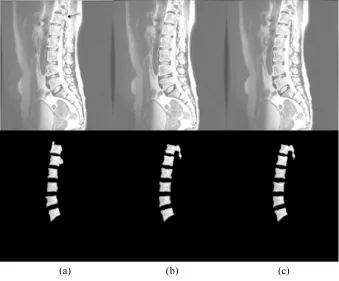
图4 分割的椎体轮廓（上）和分割的椎体（下）。（a）NJW算法；（b）本算法；（c）手动分割Fig.4 The contours（upper）and the segmentations of the vertebral bodies（bottom）.（a）NJW algorithm；（b）the proposed algorithm；（c）manual segmentation

4.4 实验4

患者椎体病变，椎体退行性改变，椎间盘突出（T2加权图像）

随着年龄的增大，脊椎也会发生病变，如椎体退行性改变（图5（a）中黑色箭头所示），椎间盘突出（图5（a）中白色箭头所示）。由于成像技术的影响，图5椎体上还有亮斑。此类脊椎MR图像的分割结果稍微变差，NJW算法不能准确地分割出退行性改变的椎体；即使椎体形状发生变化，本算法也能较为准确地分割出脊椎，光滑且清晰，分割椎体轮廓和椎体形状较为接近。从表1可知，本算法和手动分割算法较为接近。

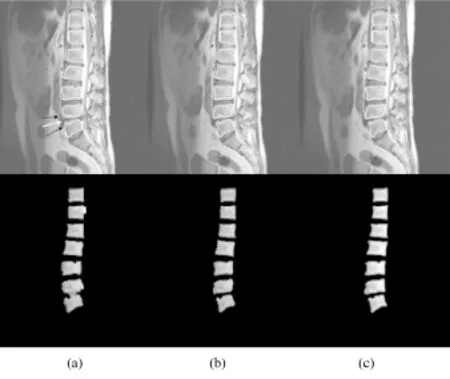
图5 分割的椎体轮廓（上）和分割的椎体（下）。（a）NJW算法；（b）本算法；（c）手动分割Fig.5 The contours（upper）and the segmentations of the vertebral bodies（bottom）.（a）NJW algorithm；（b）the proposed algorithm；（c）manual segmentation

为了客观评价本算法的可行性，表1列出了手动分割算法和本研究提出的自动分割算法的比较结果。

表1 手动和所提出的自动分割算法比较Tab.1 The comparison between the manual segmentation and the proposed algorithm

作为一种一般性的分割方法，本算法还可拓展到其他器官的分割中，图6为3种不同算法分割的脑部肿瘤，NJW算法分割的脑部肿瘤边缘不光滑。图7为本算法用于3张不同患者的脑部肿瘤分割图。

4 讨论和结论

基于图论的图像分割技术是一种新的分割技术，在医学图像的处理领域还处于初步研究阶段。NJW算法构造相似度矩阵时，仅仅用单个像素的特征值，不足以很好地描述一幅图像，并且需要做大量的实验，以得到合适的尺度参数，提高分割精度。当一幅图像的像素分布在不同的尺度空间时，即使在获得一个合适的尺度参数的情况下，也得不到理想的分割效果。正如实验结果所示，对于椎体和毗邻组织灰度相近的图像和椎体发生退行性形变的图像，其分割效果不理想，椎体不能准确地分割出来，在轮廓处出现了过分割和欠分割现象。

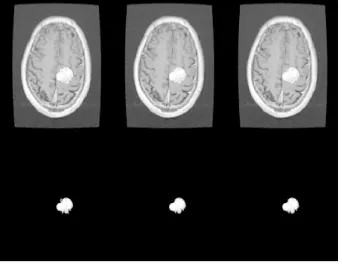
图6 分割的脑部瘤轮廓（上）和分割的肿瘤（下）。（a）NJW算法；（b）本算法；（c）手动分割Fig.6 The contours（upper）and the segmentations of the brain tumors（bottom）.（a）NJW algorithm；（b）the proposed algorithm；（c）manual segmentation

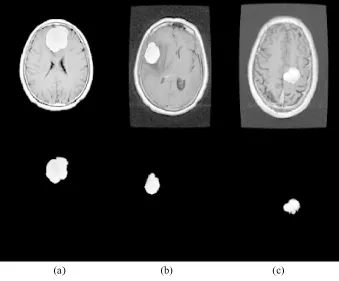
图7 本算法的脑部肿瘤分割结果。（a）患者1；（b）患者2；（c）患者3Fig.7 The segmentations of the brain tumors（the proposed algorithm）.（a）Patient 1；（b）Patient 2；（c）Patient 3

笔者提出的算法充分考虑到了像素周围邻域对每个像素点的影响，引入了空间结构信息，把邻域信息根据经验以一定的特征权重结合到一起，即用高斯函数加权的χ2距离，度量两个像素节点的相似度大小，从而构造了一个新的相似度矩阵，提高了聚类和分割的结果。在选择尺度参数时，本算法引入了局部收缩思想，自动地为每一个像素点赋一个尺度参数，使得算法自适应于图像分割，即使当一幅图像的像素分布在不同的尺度空间时，算法仍具有自适应调节性。正如实验结果所示，在自动分割脊椎MR图像的椎体时，对椎体和毗邻组织灰度相近的图像、脊柱侧凸、手术后椎间盘变形、移位等图像仍有很好的分割结果，鲁棒性强。作为一种一般性的分割方法，可以拓展到其他组织的分割中。

脊椎MR图像的分割一直是个难点，其基于邻域信息和高斯卡方距离的椎体MR图像分割方法分割的椎体轮廓和手动分割较为接近，且不需要反复调整参数，准确的分割结果对于图像配准、图像检索、脊椎畸形的分析、器官定位和相关疾病的辅助诊断具有重大的应用价值。

［1］吴剑，肖汝，吴建华.脊椎图像分割和配准的研究进展［J］.中国康复理论与实践，2010，16（02）：130-133.

［2］Baillard C，Hellier P，Barillot C.Segmentation of brain 3D M R images using level sets and dense registration［J］.Medical Image Analysis，2001，5（3）：185-194.

［3］Kass M，Witkin A，Terzopoulos D.Snakes：active contour models［J］.International Journal of Computer Vision，1987，1（4）：321-331.

［4］Kanungo T，Mount D，Netanyahu N，et al.An efficient kmeans clustering algorithm：analysis and implementation［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2002，24（7）：881-892.

［5］Gamio J，Belongie S，Majumdar S.Normalized cuts in 3D for spinal MRI segmentation［J］.IEEE Trans on Medical Imaging，2004，23（1）：36-44.

［6］Zelnik ML，Perona P.Self-tuning spectral clustering［C］//Weiss Y，Scholkopf B，Platt J.，eds.Advances in Neural Information Processing Systems（NIPS）.Cambridge：MTT Press，2004：1601-1608.

［7］Wu Zhenyu，Leahy R.An optimal graph theoretic approach to data clustering：theory and its application to image segmentation［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，1993，15（11）：1101-1113.

［8］Shi Jianbo，Malik J.Normalized cuts and image segmentation［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2000，22（8）：888-905.

［9］Ng A，Jordan M，Weiss Y.On spectral clustering：analysis and an algorithm［C］//Weiss Y，Scholkopf B，Platt J，eds.Advances in Neural Information Processing Systems（NIPS）.Cambridge：MTT Press，2002：857-864.

［10］Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，1990，12（7）：629-639.