Affymetrix基因芯片原始数据噪声分析与应用

金圣华 刘学军 张 礼（南京航空航天大学 计算机科学与技术学院，南京 2006）

2（淮阴工学院 计算机工程学院，淮安 223001）

引言

随着人类基因组计划的完成，使人类及其他多种生物的核苷酸构成得以测序。科学家们研究的重点转为分析这些基因的功能以及基因之间的相互关系，希望通过认识基因互相作用的机理来揭示生命的奥秘，进而延长人类的寿命，提高人类的生活质量。为了研究基因之间复杂的调控关系，近10多年来，人们采用高通量的方法，在基因组水平上大规模测量基因的表达水平。基于杂交技术的基因芯片［1-2］以其高度并行化、多样化、微型化和自动化的特征快速地发展起来，在生命科学以及生物医学领域得到广泛应用。目前，对基因表达数据的分析主要分为两个步骤：基因芯片实验的原始数据分析为每个基因计算一个表达值，也称为探针级别数据分析；后续分析以此作为输入数据，进行多种目的的分析工作，如寻找差异基因、聚类、分析调控网络等。因此，原始数据分析的准确程度，对后续分析起着至关重要的作用。

基因芯片技术出现的时间较长，技术相对成熟，但是采用基因芯片进行基因表达水平测量存在一个主要的问题：由于实验中非特异性杂交的存在，使得实验结果包含较高噪声，影响了基因表达水平的计算。过去几年的研究表明，可以采用各种数学模型对噪声来源进行模拟，以便有效去除噪声对后续数据分析的影响。本研究使用目前使用较为广泛的美国Affymetrix公司制备的基因芯片GeneChip®，对原始实验数据进行分析研究。首先，利用Affymetrix公司提供的一个标准的拉丁方spike-in数据集［3］，分析原始数据的噪声特征，研究芯片的物理结构和噪声之间的关系，归纳出相应的表示方式，将此对应关系应用到目前一个先进的计算基因表达水平的概率模型mmgMOS中［4］；最后采用拉丁方spike-in实验数据集及一个真实的老鼠胚胎数据集［5］，对改进的mmgMOS模型进行实验验证。实验结果显示，考虑了芯片物理结构和数据噪声的关系，可以有效地提高mmgMOS方法对基因表达水平计算的精度和效率。

1 基因芯片实验原理

基因芯片是在一个方形的固体平面上固定大量称之为探针的短序列，探针与基因或基因的产物等在一定条件下发生杂交反应。芯片实验是从生物样本中提取mRNA，将mRNA逆转录成cDNA，然后与芯片上的探针进行杂交，把配对后的芯片进行冲洗、扫描，得到探针水平的原始数据。目前，广泛使用的芯片主要是美国Affymetrix公司的寡聚核苷酸基因芯片。Affymetrix公司使用原位合成的方法，设计了独特的PM-MM探针方案：每一个基因在芯片上对应一个或几个探针组，每个探针组又由十几对25mer的探针对组成，每探针对包括两个探针，其中一个是完全匹配（PM，perfect-match）的探针，另一个是序列中间有一个碱基错配（mis-match，MM）的探针［2］。每个探针组在实验结果中，PM和MM探针的荧光灰度值代表所对应基因的表达水平。根据杂交原理，探针理论上只与样本中碱基互补的mRNA单链进行杂交，这种绑定称为特异性杂交（specific hybridization）。但是，实际实验中与探针序列不完全匹配的mRNA样本序列也可能与该探针杂交绑定，称为非特异性杂交（non-specific hybridization）。GeneChip®中MM探针的引入，是为了测量对应PM探针的非特异性杂交信号。

2 标准拉丁方spike-in实验数据集

该数据集由美国Affymetrix公司提供，以便研究和比较探针级别数据分析方法。采用HGU-133基因芯片，含有42个spike-in基因、14组标靶浓度下重复3次的实验数据，以拉丁方实验模式得出的数据。数据集中每个基因芯片为712×712矩阵，包含506 944个探针，一共有22 300个探针组。第一组实验的样本浓度顺序为0、0.125、0.25、0.5、1、2、4、8、16、32、64、128、256、512皮摩尔（pM），以后每组实验轮转一下浓度顺序。例如，第二组实验的样本浓度顺序为0.125、0.25、0.5、1、2、4、8、16、32、64、128、256、512、0pM。14组已知转录组浓度的信息表提供了14个相关探针组的真实表达水平值，从而成为评价不同基因表达水平算法性能的标准。

图1 在Affymetrix HGU-133 spike-in数据集中，204563_s_at探针组有11个探针对其实验结果和样本浓度的对应关系（实线代表PM探针的对数灰度值，虚线代表MM探针的对数灰度值）Fig.1 The logarithm of the intensities for the 11 probe pairs related to probe-set 204563_s_at in Affymetrix HGU-133 spike-in dataset versus the logarithm of transcript concentration（The solid lines represent PM intensities and the dotted lines represent MM intensities）

3 原始数据噪声特征分析

在spike-in数据集中，随机选取一个spike-in探针组204563_s_at，其样本浓度和探针灰度值之间的关系见图1。该探针组有11个探针对，实验浓度为0、0.125、0.25、0.5、1、2、4、8、16、32、64、128、256、512pM。

由实验结果可知，当样本的浓度增大时，PM和MM探针的灰度值都随之增加，这意味着PM和MM探针均测量到对应基因的特异性杂交信号，但PM探针的灰度增加要比相应的MM探针的灰度大；当样本浓度降低时，同一探针对的PM和MM的灰度是很接近的，少部分MM探针的灰度值大于PM探针的灰度值。有研究者发现，这部分探针对应整个数据集的10％～30％［6］。另外，探针灰度值和样本浓度并不总是成线性关系，特别在低浓度的时候。这是由于样本浓度较低时，探针灰度值中测得的特异性杂交信号较少，非特异性杂交和背景噪声对实验结果影响较大，所以对基因表达水平的计算比较困难。由以上分析可知，MM探针也测量到对应基因的真实信号，因此进行以下假设，有

式中：pm和mm分别为PM和MM探针在实验结果中对应的图像灰度值，代表待测相应基因的该mRNA片段的转录水平；s为特异性杂交信号，即与PM探针完全匹配的杂交信号；b为非特异性杂交信号和背景噪声。

有学者通过实验验证，相比非特异性杂交信号，特异性杂交信号的背景噪声比较小，可以忽略，也可预先去除［11］。在式（1）中，系数Φ∈（0，1）。该假设允许MM探针也测量到部分特异性杂交信号，这与图1观测到实验结果是相符的。同时假设，绑定在MM探针上的特异性杂交信号小于PM探针上的特异性杂交信息。当样本浓度较大时，由于探针灰度中的特异性信号较大，所以可将此时的非特异性杂交信号和背景噪声忽略不计，则式（1）可近似为

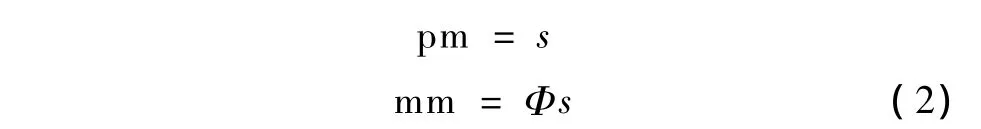
此时，可认为log2mm≈log2Φ+log2pm或Φ≈mm/pm。当样本浓度较大时，log2pm与log2mm曲线近似平行，之差即为log2Φ。由图1还可发现，每个探针对应的log2Φ大小不尽相同，希望能够找到不同探针所对应的Φ，以便得到MM探针上测量到的特异性杂交信号的比例。

有研究者发现，Affymetrix基因芯片探针中央核苷酸序列和相应MM探针与PM探针灰度比值存在一定关系［7-8］。根据GeneChip®设计原理，PM和MM两个探针结构上的差别仅是中央一个核苷酸是错配的。从spike-in数据集中，提取浓度值大于64pM的spike-in基因所对应的探针灰度值，得到探针中央一个核苷酸对应的MM探针灰度与PM探针灰度比值分布的直方图，如图2所示。由于提取数据所对应的样本浓度较高，所以可以忽略非特异性杂交和背景噪声的影响，该直方图可以近似给出Φ的分布情况。从图2中可以发现，中央核苷酸C和G的Φ分布较相似，这意味着探针中央一个核苷酸所对应的Φ分布不惟一，因此选取探针中央3个核苷酸来研究核苷酸序列和Φ之间的关系。从spike-in数据集中提取浓度值大于64pM的基因表达值，得到探针中央3个核苷酸所对应的Φ分布情况，图3显示了部分分析结果。从图3中可以看出，Φ在大部分情况下小于1，这说明大部分MM探针的灰度值小于PM探针的灰度值，并且Φ的分布因核苷酸组合的不同而明显不同，表明Φ的分布与中央3个核苷酸序列具有一定相关性。

图2 样本浓度值大于64 pM的探针中央一个核苷酸对应MM探针灰度与PM探针灰度的比值直方图Fig.2 The histogram of the ratio ofmm/pm with identical middle nucleotide within the probe-pairs PM and MM probes are from the sample concentrations are greater than 64 pM

4 对探针级别数据分析算法的改进

根据Affymetrix基因芯片原始数据的噪声特性，人们设计了很多模型来计算基因的表达值。传统方法主要有MBEI［9］、RMA［10］和GCRMA［11］等，能够较为准确地计算出基因表达水平，但是大部分仅计算出表达值而不能提供表达值的置信区间给后续分析。而概率模型在处理基因原始表达数据时［12］，不仅能给出每个基因的表达值，而且还能给出每个表达值的置信度，为后续分析提供更多信息，如BGX［13］、gMOS［14］和mmgMOS。其中，BGX考虑到了MM探针上也测量到特异性杂交信号，但是BGX通过MCMC方法来估计模型中的参数，因此计算效率比较低，特别是对于低表达值的基因，需要更多次的迭代。gMOS和mgMOS这两个模型，利用最大似然估计参数的方法，提高了计算速度，但是只针对单个芯片，假设芯片之间没有相关性，并且没有考虑MM探针上也测量到了真实信号，这显然是不合实际的。mmgMOS模型结合BGX模型和mgMOS模型的优点［15］，同时考虑了相同的探针在不同芯片上具有同样的相关性。该模型假设

图3 样本浓度值大于64pM的探针中央3个核苷酸对应MM探针灰度与PM探针灰度比值直方图Fig.3 The histogram of the ratio of mm/pm with identical middle three nucleotides within the probe-pairs.PM and MM probes are from the sample concentrations are greater than 64 pM

式中，pmgjc和mmgjc分别表示芯片c上探针组g的第j个PM和MM探针对的灰度值，sgjc表示特异性杂交信号，bgjc表示非特异性杂交信号和背景噪声。该模型是将每个芯片上最小探针灰度值近似作为背景噪声［11］，在应用式（3）之前，将其从PM和MM探针灰度中去除，故经过背景噪声矫正，bgjc仅表示非特异性杂交信号。式（3）中Φ∈（0，1），表示MM探针上也测量到了一部分特异性信号。但是，该模型假设所有探针对具有相同的Φ系数值，没有考虑到不同探针灰度值对应的Φ是不同的。其中，Φ的求解采用MAP估计与其他参数进行交替迭代，计算效率较低。

通过对原始数据的分析，发现不同核苷酸序列对应不同的MM探针灰度与PM探针灰度的比值（Φ≈mm/pm）。对于探针中央3个核苷酸的64种组合形式，求出每种组合所对应的Φk值，k对应探针中央3个核苷酸的组合情况。将此对应关系嵌入到mmgMOS中，得到新模型mmgMOSⅡ，有

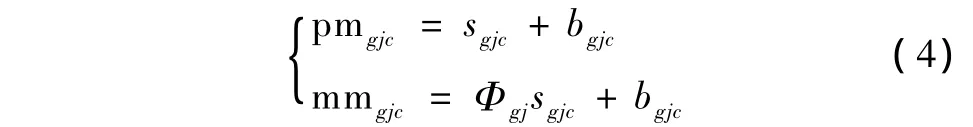
式中，Φgj是和每个探针组中的每个探针对应，取值为中央3个核苷酸的64种可能组合所对应的MM探针灰度与PM探针灰度比值之一，同类芯片可以共享该值，表示绑定在该芯片上的每个MM探针特异性杂交信号的比例。

利用此模型，可以消除实验中MM探针测量到的真实信号对基因表达水平计算带来的影响，从而提高基因表达水平计算的准确率。其中，Φgj不参与模型的求解，可以通过对实验数据的预处理而近似得到，消除了原来mmgMOS模型中反复迭代求解的过程，提高了计算的效率。

5 实验结果分析

为了验证mmgMOSⅡ模型在计算效率和计算精度两方面的性能，分别采用spike-in数据集以及一个真实的老鼠胚胎数据集。除了与mmgMOS方法进行比较外，因传统方法MBEI同样能输出基因表达水平的置信区间，故也与该方法进行比较。MBEI采用Affy软件包中的实现代码，mmgMOS采用Bioconductor中puma软件包的实现代码［16］，mmgMOSⅡ是在mmgMOS的实现基础上进行修改。

5.1 计算精度

5.1.1 Spike-in数据集上的性能比较

对spike-in数据集处理，mmgMOSⅡ采用了样本浓度大于64pM的探针灰度值计算Φk值，mmgMOS对所有探针共享的Φ进行优化计算，MBEI仅使用PM探针灰度值来计算。图4显示了42个spike-in基因利用不同方法求出的基因表达值和样本浓度之间的对应关系，采用的数据为每个条件下选取3次重复实验中的1次测量值。随着样本浓度的增大，得到的基因表达水平对应增大，图4中每条曲线的斜率理论上为1。然而，在样本浓度较低的情况下，由于mmgMOSⅡ和mmgMOS计算得到的部分基因表达值小于1，使得对数表达值为负值。而MBEI只使用PM探针灰度值，因此没有负表达值，得到较高的基因表达水平。取浓度范围为2、4、8、16、32pM，得基因表达值和样本浓度的比值如图4中的Slope所示。可以看出，mmgMOSⅡ和mmgMOS得到的平均斜率相比于MBEI更接近于1，而mmgMOSⅡ相对于mmgMOS结果略优越。

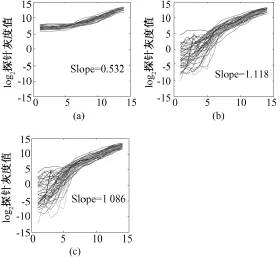
图4 42个Spike-in基因在Spike-in数据集上利用不同方法求出的基因表达值和样本浓度值之间的对应关系。（a）MBEI；（b）mmgMOS；（c）mmgMOSⅡFig.4 Curves of logarithm of gene expression values obtained from different methods，for the 42 spike-in genes in the spike-in data set spike-in against the log transformation of transcription concentrations.（a）MBEI；（b）mmgMOS；（c）mmgMOSⅡ

5.1.2 老鼠胚胎数据集上的性能比较

利用GEO（the Gene Expression Omnibus）数据库中老鼠胚胎的真实数据集，进一步验证mmgMOSⅡ的性能。老鼠胚胎数据集使用Affymetrix Mouse Genome 430 2.0基因芯片，用来判断Oct4估测基因在老鼠早期胚胎中从单细胞到多细胞阶段变化过程的规律。这个数据集包括4个实验条件，每个条件下有3个重复芯片，每个芯片上包含45 037个探针组。4个条件由测试实验和对照实验两部分组成，其中测试实验包括注射了Oct4和Ccna2两个部分，而对照组对应着没有注射的两部分。在Oct4实验条件下，总共有42个基因被选择出来进行反转录酵素-聚合酵素连锁反应（qr-PCR）实验，qr-PCR实验证明32个差异基因对应芯片上的93个匹配的探针组。用这93个显著差异的探针组作为判断标准，比较不同基因表达水平计算方法得到的处理结果。其中，寻找差异基因处理的方法全部采用PPLR［17］，该方法不但采用基因表达水平测量值来寻找差异基因，同时还利用了基因表达水平的置信区间，更好地利用了原始数据中的丰富信息。mmgMOSⅡ分别选取PM探针灰度值大于512和1 024的实验数据来预计算Φk。为了使不同的处理结果可以互相做比较，分别选取不同α水平值。这里的α没有特殊的意义，只是保证每种方法找到的总差异基因个数为1 254个。

表1中显示了不同方法找到的与93个PCR实验验证的差异探针组一致的差异基因数。对于MBEI+PPLR方法，测得与qr-PCR数据一致的探针组为33个，其一致率为35.5％；对于mmgMOS+PPLR方法，测得与qr-PCR数据一致的探针组为38个，其一致率为40.9％；对于mmgMOSⅡ+PPLR方法，在Φk的计算选取PM探针灰度值大于512和1 024的两种情况下，均检测到40个，其一致率为43.0％。实验结果表明，在真实数据集的处理中，mmgMOSⅡ能够比mmgMOS及传统方法MBEI显著降低原始数据中噪声的干扰。

表1 老鼠胚胎真实数据集的检测结果Tab.1 Results on the real mouse embryo dataset

5.2 计算效率

为了验证mmgMOSⅡ的计算效率，比较了mmgMOS和mmgMOSⅡ对不同数据集的处理时间。表2列出两种方法在不同数据集上的计算时间，计算平台为双核CPU，主频2.60GHz，2.0GB内存，Windows XP操作系统。

从表2中可以看出，mmgMOSⅡ的计算效率比mmgMOS明显提高。这是由于mmgMOS需要经过多次反复迭代，才能找到最后的优化值Φ，所以耗时比较长，特别是如果初始值的设置明显偏离最后的优化值，迭代的次数越多，耗时越长。在实验中，根据先验知识设置Φ初始值为0.171，spike-in数据集Φ的最后优化值为0.161 8，老鼠胚胎数据集Φ的最后优化值为0.118 04，老鼠胚胎数据集的芯片个数少于spike-in数据集，但是老鼠胚胎数据集却比实际spike-in数据集多耗费了近5h。这主要是由于该数据集Φ初始值偏离最终的优化值较大。在实际采用mmgMOS处理真实数据时，由于Φ的初始值很难确定，故通常引起较长的计算时间。而在mmgMOSⅡ中，利用预处理得到的探针中3个核苷酸序列和Φ的对应关系，可大大缩短计算时间，提高了计算效率。

表2 mmgMOSⅡ和mmgMOS在老鼠胚胎数据集和spikein数据集上的计算时间（单位：h）Tab.2 The computation time（in hours）ofmmgMOSⅡandmmgMOS on the spike-in data set and the mouse embryo dataset

6 结语

本研究分析了Affymetrix基因芯片原始数据的噪声特点，利用基因芯片探针的核苷酸序列和相应MM探针与PM探针灰度比值存在的对应关系，改进mmgMOS模型中的参数Φ的计算，最后通过spike-in标准数据集和老鼠胚胎真实数据集进行验证。实验结果证明mmgMOSⅡ能够提高原模型以及传统方法对非特异性杂交信号的处理能力。在实际采用mmgMOSⅡ处理真实数据集时，可采用灰度值较高的探针数据近似预估计Φ，避免了原方法中的参数迭代优化过程，有效提高了模型的计算效率。

［1］Schena M，Shalon D，Davis RW，et al.Quantitative monitoring of gene expression pattterns with a complementary DNA microarray［J］.Science，1995，270（5235）：467-470.

［2］Lockhart DJ，Dong H，Byrne MC，et al.Expression monitoring by hybridization to high-density oligonucleotide arrays［J］.NAT Biotechnol，1996，14（13）：1675-1680.

［3］Cope LM，Irizarry RA，Jaffee HA，et al.A Benchmark for Affymetrix GeneChip Expression Measures［J］，Bioinformatics，2004，20（3）：323-331.

［4］Liu Xuejun，MiloM，Lawrence DN，etal.A tractable probabilistic model for Affymetrix probe-level analysis across multiple chips［J］.Bioinformatics，2005，21（18）：3637-3644.

［5］Foygel K，Choi B，Jun S，et al.A novel and critical role for oct4 as a regulator of the maternal-embryonic transition［J］.PLOS ONE，2008，3（12）：e4109.

［6］Chudin E，Walker R，Kosaka A，et al.Assessment of the relationship between signal intensities and transcript concentration for Affymetrix GeneChip arrays［J］.Genome Biology，2001，3（1）：0005.1-0005.10.

［7］Naef F，Magnasco MO.Solving the riddle of the bright mismatches：Labeling and effective binding in oligonucleotide arrays［J］.Phys Re.E，2003，68（1）：011906.1-011906.4.

［8］Zhang L，Miles MF，Aldape KD.A model of molecular interactions on short oligonucleotide microarrays［J］.Nature Biotechnology，2003，21（7）：818-821.

［9］Li C，Wong W.Model-based analysis of oligonucleotide arrays：Expression index computation and outlier detection［J］.Proc Natl Acad Sci USA，2001，98（1）：31-36.

［10］Irizarry RA，Hobbs B，Collin F，et al.Exploration，normalization，and summaries of high density oligonucleotide array probe level data［J］.Biostatistics，2003，4（2）：249-264.

［11］Wu Zhijin，Irizarry RA，Gentleman R，et al.A model-based background adjustment for oligonucleotide expression arrays［J］.J AM Stat Assoc，2004，99（468）：909-917.

［12］Pearson R，Liu Xuejun，Sanguinetti G，et al.Puma：A bioconductor package for Propagating Uncertainty in Microarray Analysis［J］.BMC Bioinformatics，2009，10（1）：211-221.

［13］Hein，Anne-Mette K.BGX：a fully Bayesian integrated approach to the analysis of affymetrix genechip data［J］.Biostatistics，2005，6（3）：349-373.

［14］Milo M，Fazeli A，Niranjan M，et al.A probabilistic model for the extraction of expression levels from oligonucleotide arrays［J］.Biochem.Soc.Trans，2003，31（6）：1510-1512.

［15］Liu Xuejun，Lin KK，Andersen B，et al.Including probe-level uncertainty in Model-based gene expression clustering［J］.BMC Bioinformatics，2007，8（98）.98-106.

［16］Rattray M，Liu Xuejun，Sanguinities G，et al.Propagating uncertainty in Microarray data analysis［J］.Brief Bioinform，2006，7（1）：37-47.

［17］Liu Xuejun，Milo M，Lawrence ND，etal.Probe-level measurement error improves accuracy in detecting differential gene expression［J］.Bioinformatics，2006，22（17）：2107-2113.