大膨胀比火箭发动机喷管流动分离与气动弹性分析①

胡海峰，鲍福廷，蔡 强，刘 旸

(西北工业大学航天学院，西安 710072)

0 引言

目前的运载助推级动力系统，为了发挥发动机的性能潜力，采用的喷管膨胀比越来越大。大膨胀比的喷管在地面试车及发动机的起动和关机过程中，都会产生气流分离现象。气流分离模态的转涙，导致在瞬变状态下喷管内三维气流的分离流动常呈现复杂的非轴对称性，可能引发喷管侧向载荷。严重的喷管侧向载荷会造成喷管震动、发动机使用寿命缩短、喷管结构破坏等后果。

美国的J2S发动机、航天飞机主发动机(SSME)、俄罗斯的RD-120发动机、欧洲的Vulcain发动机和日本的LE-7等发动机的研制过程中，均遇到了较严重的喷管侧向载荷问题。国外对大膨胀比的喷管性能分析计算开展了大量研究，并取得了很多有用结论。文献［1］对喷管分离流试验结果进行分析归纳，给出了判别分离流的经验公式;文献［2-3］对分离流产生的侧向载荷进行了分析仿真;文献［4-6］对影响分离流各个分离模式进行了数值仿真及实验对比分析研究;文献［7］对分离流下的喷管热性能进行了探讨;文献［8］开展了分离状态下喷管气动响应的理论探索;文献［9］对某型喷管开展了分离模式下结构气动响应的试验研究;文献［10-12］开展了分离条件下喷管流固耦合数值模拟。

本文以某大膨胀比喷管二维轴对称简化模型为分析对象，采用数值模拟方法研究其分离模式，分析在瞬变状态下喷管结构的气动弹性响应，讨论了喷管瞬态下径向位移分布。侧向载荷在三维状态下能够预示，为二维简化三维的分析提供基础，并为后续三维深入分析侧向载荷及喷管结构气动弹性响应提供支持。

1 研究对象与方法

1.1 研究对象

本研究选取VAC公司的Volvo S1喷管为研究对象［6］。该喷管为最大推力喷管，其扩张段内型面满足Rao-Shmyglevsky方程:

几何构型见图1，几何参数见表1。

图1 喷管基本构型简图Fig.1 Basic nozzle geometry sketch

表1 计算几何结构基本参数Table 1 calculation geometry data

1.2 流场数值计算方法

本文采用SA湍流模型，求解直角坐标系下二维稳态雷诺时均N-S方程。这是由于该模型相对于一般的两方程湍流模型，对逆压梯度下的分离流动有着更为准确的模拟。该湍流模型对壁面网格节点的要求更为严格。因此，采用结构化网格，壁面网格局部加密，保证第一层网格的y+接近于1，并保证在有粘性影响的近壁面区域(Rev＜200)内，至少有10个单元网格，网格均匀过渡。对N-S湍流时均方程，采用耦合隐式求解;对各参数的离散，采用二阶精度的迎风格式。为准确描述理想气体各物性，数值计算中根据经验多项式进行定压比热容计算，气体粘性系数由三系数的Sutherland定律给定。Sutherland定律具体形式为

式中 T0为参考温度，取为273.11 K;S为等效温度，取为110.56 K;μ0为 T0时的参考粘性系数，取为1.716×10-5kg/(m·s)。

1.3 网格无关性验证

分离流对网格密度有很强的依赖性，本文在计算获得稳态解的基础上，对网格进行加密对比计算结果。当网格加密后，计算结果不发生变化，即认为计算得到的收敛解与网格无关。本文在保证壁面y+接近1的前提下，计算得到收敛解，然后对网格加密，适当调整网格间距。为区别比较，本文在流向及垂直流向方向(径向)加密。本文列举燃烧室总压与环境背压比值(NPR)为14、16两种工况进行对比分析。表2所示为具体的喷管区域给出网格的分布及总网格数，外流场网格数据未列举。

表2 NPR=14、16时计算模型网格数Table 2 Grid disributions when NPR=14，16

图2、图3分别为NPR=14、16时，计算2组不同疏密条件下得到的稳态收敛解中喷管壁面压力分布与试验数据的对比曲线。由图2、图3可直观看出，计算结果和试验结果吻合较好。在网格加密后，壁面压强分布和之前相对较稀疏网格比较基本没有变化。说明在计算过程中，得到的稳态收敛解和网格无关，基本揭示了真实的喷管内部流动。

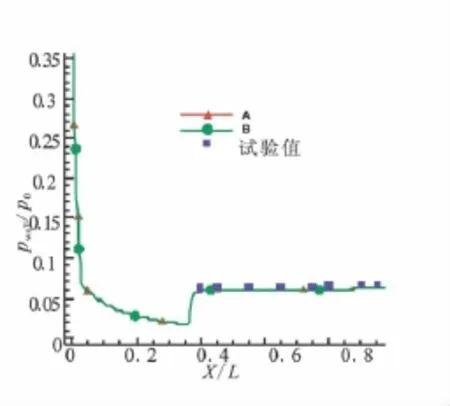
图2 NPR=14下不同网格类型下喷管壁面压力分布线Fig.2 Nozzle wall pressure when NPR=14

图3 NPR=16下不同网格类型下喷管壁面压力分布线Fig.3 Nozzle wall pressure when NPR=16

1.4 流场结构分析

该数值模拟部分对 NPR 分别为 8、10、12、14、16.4、21、25、30、35、40、45、50 等 12 种工况，按照上述的数值方法进行仿真分析。每个工况均以上一计算结果为初值。结果表明，入口压强由高到低不同工况下，喷管流场先后出现2种不同的激波分离模态:自由激波和受限激波分离，如图4所示。2种不同激波分离模态下，喷管内流场及压强分布情况等呈现不同特点。图4中，a为马赫盘;b为斜激波;c为受限激波;d为内激波。

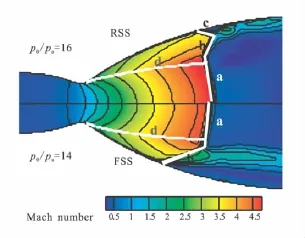
图4 自由激波和受限激波简图Fig.4 Schematic illustrations of FSS and RSS

1.4.1 自由激波(FSS)

图4所示自由激波结构简图中，喷管内的气流由壁面分离后，向外延伸流出喷管，由于喷管膨胀比较大，喷管内气流处于过膨胀状态，燃烧室总压与环境背压之比较小，导致在喷管内部出现激波。但由图4可看到，气流经过正激波a及斜激波b后，在内部形成马赫盘，壁面的气体分离后，未附着在壁面上。同时，随燃烧室总压的提高，喷管内部的激波往喷管出口移动，但在激波前，流场的参数基本不变。

图5为燃烧室在自由激波模态下喷管扩张段的壁面压强分布曲线。由图5可看出，在自由激波模式下，壁面出现分离后，压强经过激波迅速上升到环境压强大小。

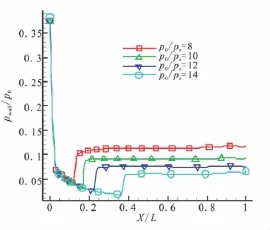
图5 自由激波阶段喷管壁面压强分布Fig.5 Profile of the pressure distributionsalong the nozzle wall

1.4.2 受限激波(RSS)

图4所示受限激波结构简图中，分离后的激波附着到了喷管壁面，形成一个附着回流区。

图6所示为燃烧室在受限激波模态下，喷管扩张段的壁面压强分布。

图6 受限激波阶段喷管壁面压强分布Fig.6 Distributions of the pressure along nozzle wall during the RSS model

由图6可看出，壁面压强同样首先随气流膨胀逐渐降低，在分离点由于分离斜激波的作用，壁面压强迅速升高到一个相对稳定压强(图6中所示平台区域)。与自由激波分离不同的是短暂分离后，气流再次附着到壁面。由于再附着激波的强烈作用，在再附着点壁面压强急剧升高到超过环境压强。此后，壁面压强通过一系列逐渐减弱的波动，最终回落到略低于环境压强，直到喷管出口。这种逐渐减弱的压强波动是由于激波的反射特性造成的。再附着激波有反射离开壁面的趋势，这种趋势的强弱由激波的强弱决定，由此造成气流在远离和靠近壁面之间反复，在受限区域内形成了菱形激波串，进而引起壁面压强的波动。

上述两种不同的分离模态下，每种分离激波模态喷管内部都会产生一道内激波(图4中d曲线)。这道内激波源于喷管抛物线型面起始点。最大推力喷管的设计方法，决定了喷管型面在这一点为二阶不连续点，是一个流动不稳定点，容易产生激波。图4流场结构示意图表明，这道内激波将在很大程度上决定中心区激波的形态。中心区流场正激波后的涡流具有推动流动向壁面发展的趋势。当流体朝向壁面流动的动量达到一定程度时，便产生了分离再附着现象。

1.5 流固耦合分析计算

本文基于计算流体力学(CFD)和计算结构动力学(CSD)的时域耦合仿真方法，分析喷管流固耦合气动弹性问题。通过非定常计算流体力学求解器，直接计算喷管壳体在任意时刻的非定常载荷，包括热和气动力，在时域内推进结构运动方程，给出喷管壳体结构的详细时间响应历程。

根据流场和结构两个独立域求解的时间同步推进技术，文献［13］将CFD/CSD耦合分为全耦合、紧耦合、松耦合3种方式。本文采用松耦合，其流体计算与结构计算在时间上耦合基本逻辑见图7。

在流场计算方面，通过前述方法计算N-S方程;在结构场计算方面，求解结构静力学平衡方程。

流固耦合计算关键在于流固交界面的处理［14］，流固交界面上数据需双向交互。流场对固体区域的作用，包括力的作用等载荷。计算时，在一个时间步内，首先计算流场，然后将流场的作用通过流固交界面加载到固体区域，计算出固体的温度场和应力应变，如果变形较大，则改变流固界面。基于无限插值(transfinite interpolation)的变形网格技术方法，重新生成计算区域的网格，进行下一个时间步的计算。具体如图8所示。

图7 CFD/CSD松耦合结构示意图Fig.7 CFD/CSD loose coupled structure

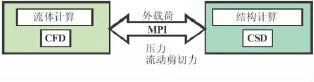
图8 流固耦合表面数据交互Fig.8 Data exchanged of the FSI interface

为了提高计算效率，采用并行化的MDICE［15］并行计算环境，遵照MPI(Message Passing Interface)规范，实现计算过程中各不同模块数据在不同进程间的数据传递。CFD/CSD松耦合的具体流程见图9。

图9 CFD/CSD松耦合程序流程示意图Fig.9 Flow chart of the CFD/CSD loosely coupled

计算喷管壳体应力分布时，首先求解在外力作用 下应变的分布，再通过应力和应变的关系，求解应力的分布。外力和应变之间的关系，通过虚功原理建立平衡方程。假设是作用在喷管壳体计算单元上的外力，通过虚功原理建立壁面的力学平衡方程。节点虚位移为则外力所做的功为

2 仿真结果分析

计算中，取喷管壳体壁厚为等厚度，具体材料属性及厚度如表3所示。模拟喷管入口压力为3 MPa的瞬态起动工况，分析该过程中喷管壳体的气动响应问题。

图10所示为发动机工作起动阶段不同时刻流场速度云图和喷管壳体径向位移变形云图显示。由图10可看出，在喷管起动过程中，壳体在内压作用下沿径向出现变形微小变形，在1×10-6m量级水平。分析可能的原因为燃烧室内3 MPa压强偏低，喷管壁厚11 mm较厚，同时2 ms作用时间极短，导致径向形变较小。同时，不同时刻壳体径向位移最大的也不是在壳体的末端。随喷管内部压强的建立，喷管不同部分的变形不尽相同。由云图显示部分可看出，在喷管收敛段部分，由于其压强较高，导致该段变形较大。

表3 喷管壳体材料数据Table 3 Property of the nozzle case material

图10 不同时刻喷管内部流场和喷管壳体结构变形云图Fig.10 Contour of the flow inside nozzle and deformation of nozzle case at different times

图11所示为喷管壳体末端的径向位移随时间的变化曲线。可看出，在喷管起动阶段，末端变形位移最大，随喷管内部流场建立，在端点的位移逐渐退化为震荡变形。但由图示幅值可看到，在模拟时间内，位移均为负值，模拟仿真的时间较短，仿真时间段内未形成周期变化。图示端点位移振荡并非是周期性，这是因为在燃烧室室压3 MPa条件下，喷管内分离状态为受限激波，分离条件下的气流再附着到壁面，再分离再附着循环，直至气流流出喷管，在附着区域内压强出现变化，导致其壁面受力复杂，最终表现为结构振荡。

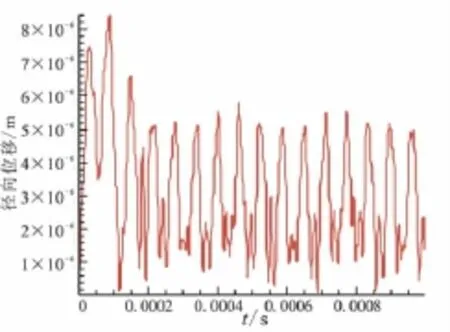
图11 喷管端点径向变形随时间变化曲线Fig.11 Point at the end of the case radial direction deformation vs the time

3 结论

(1)对于本文计算的给定喷管构型，在燃烧室与喷管出口压强之比(NPR)变化过程中，喷管内出现了自由激波和受限激波2种分离模态。不同的分离模态，导致喷管壁面承受不同的压力分布。

(2)在对流动的分析基础上，结合CFD/CSD耦合分析方法，分析了分离情况下喷管壳体的气动弹性问题。结果表明，在起动过程中，随喷管内部压强建立，喷管不同部分出现不同的结构变形。在喷管扩张段，其承受的压力较高、变形较大，喷管扩张段端点部分变形随时间并非严格意义上的周期变化。这主要是因为在受限分离下，壁面的压力出现波动。本文为后续详细分析侧向载荷提供基础。

值得指出的是喷管内部的流动较为复杂，分离状况下产生的侧向载荷通常表现为非对称性。因此，为详细揭示分离条件下结构响应，需开展三维分析。

［1］Frey M，Hagemann G.Status of flow separation pre-diction in rocket nozzles［C］//34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference ＆ Exhibit，Cleve-land，Oh，USA，July 13-15，1998.

［2］Kurt B Smalley，Andrew M Brown and Joseph Ruf.Flow separation side-loads excitation of rocket nozzle FEM［C］//48th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Con.，Honolulu，Hawaii，USA.A-pril 23-26，2007.

［3］刘亚冰，王长辉，许晓勇.喷管分离流动与侧向载荷定常数值模拟［J］.航空动力学报，2008，23(11):2115-2118.

［4］Emanuele Martelli，Francesco Nasuti，Marcello Onofri.Numerical calculation of FSS/RSS transition in highly overexpanded rocket nozzle flows［J］.Shock Waves，2010，20:139-146.

［5］Vincent Lijo，Heuy Dong Kim，Toshiaki Setoguchi，et al.Numerical simulation of transient flows in a rocket propulsion nozzle［J］.International Journal of Heat and Fluid Flow，2010，31:409-417.

［6］Jan Östlund.Flow processes in rocket engine nozzles with focus on flow separation and side-loads［R］.TRITA-MEK Technical Report，2002:9.

［7］王艺杰，鲍褔廷，杜佳佳.固体火箭发动机喷管分离流流动数值模拟及实验研究［J］.固体火箭技术，2010，33(4):406-408.

［8］Pekkari L O.Aeroelastic analysis of side load in supersonic nozzles with separated flow［C］//30th AIAA/ASME/SAE/ASEE Joint Propulsion Conference June 27-29，1994/Indianapolis，IN.AIAA 94-3377.

［9］Dr Andrew M Brown，Joseph Ruf，Darren Reed，et al.Characterization of side load phenomena using measurement of fluid/structure interaction［R］.AIAA 2002-3999.

［10］Lefrancois E.Numerical validation of a stability model for a flexible over-expanded rocket nozzle［J］.Int.J.Numer.Meth.Fluids.2005，49:349-369.

［11］Zhang S J ，Fuchiwaki T.Aeroelastic coupling and side Loads in rocket nozzles［C］//38th Fluid Dynamics Conference and Exhibit 23-26 June 2008，Seattle，Washington，AIAA 2008-4064.

［12］Luciano Garelli.Fluid-structure interaction study of the start-up of a rocket engine nozzle［J］.Computers ＆ Fluids，2010，39:1208-1218.

［13］Hurka J，Ballman J.Elastic panels in transonic flow［R］.AIAA 2001-2722.

［14］Lv X，Zhao Y，Huang X Y，et al.A matrix-free implicit unstructured multigrid finite volume method for simulating structural dynamics and fluid-structure interaction［J］.Journal of Computational Physics，2007，225:120-144.

［15］CFD-F ASTRAN V2009.0 user manual［M］.ESI CFD inc.