装备制造业绿色度评估技术研究*
尹望吾,魏吉双
(长沙理工大学 汽车与机械工程学院,湖南 长沙 410076)
装备制造业既是国民经济的支柱产业,也是环境污染和资源浪费的主要源头,因此,尽可能的减少环境污染、节约资源以及如何资源再生,是装备制造业不能回避的问题.近年来,怎样将“绿色制造”、“循环经济”、“低碳环保”、“两型化”等理论转换成可以操作的管理模式,各界专家已经作了大量研究[1-8],但是,对于装备制造业的绿色程度(简称绿色度)具体怎么评估,目前尚无成熟的技术,所以研究装备制造业绿色度评估技术,建立评估系统颇有理论和应用价值.
湖南省长、株、潭地区装备制造业种类齐全,已形成规模体系,且呈强势扩张态势.笔者在湖南省科技厅、长沙市科技局等部门的资助下,从事装备制造企业绿色度评估系统(简称评估系统)研究.综合科学发展观、新型工业化、两型社会、循环经济、绿色制造、科技创新等系列理论的要求,运用模糊数学层次分析法设计出了评估指标体系,建立了综合评价数学模型[1-2].
绿色度评估的测评指标与权重分配是具体评估的关键问题,对于不同类型企业(比如整装厂与含毛坯铸造的配件生产厂)的要求应该有所不同,为了能根据实际情况作出相应调整,项目组研发了评估系统维护和权重录入计算系统软件,供决策者们实时调整测评指标数目、修改指标名称、调整权重级差.权重分配需针对不同群体调查,如政策相关人员、企业及普通公众等,通过调查统计之后,怎样相对合理地取值,需要研究权重的分配策略.测评指标与权重分配确定之后,怎样开展评估,需要明确具体思路与流程.本文着重讨论绿色度评估的此类技术问题.
1 评估系统维护与权重录入
1.1 评估指标体系的修改
为了能够针对不同类型的企业或不同的时期实时修改评估指标体系和权重值,项目组开发了“评估系统维护和权重模糊输入”软件.如图1所示,按右键可以添加或删除目标(或指标)数目,也可修改目标(或指标)的名称.选择“分配权重”可以修改权重值,如图2所示.
评估系统权重分配既要反映本地区的政策导向,也要与整体经济发展水平及装备制造企业水平相符,还要得到企业和大众的认同,这样才能以评估为手段促进装备制造业向两型化发展.因此,权重数据既来源于理论、政策分析,也来源于调查统计.比如,“分配权重”通过对项目组全体成员调查统计,由权重系统计算得出了文献[1-2]表1括号中的权重值.

图1 评估系统维护和权重模糊输入软件Fig.1 Evaluation system maintenance and weighing fuzzy input software

图2 权重模糊输入Fig.2 Weighing fuzzy input
1.2 权重模糊录入
界面友好、简单便捷又不失精准的权重输入工具是调查统计的基础.项目组开发的工具界面如图2所示,基于定性与定量相结合的原则采用模糊输入方式.
权重模糊录入分为两个步骤:
1)比较同层指标之间的相对重要程度.如图2所示,系统先根据“经济效益”目标的下级指标数目确定等级数,依字母顺序命名,如“A,B,C,…”等.字母顺序代表重要程度,前序的较后续者重要程度较小.图2中,资本收益率与产品合格率、劳动生产率与职工人均收入两两之间同等重要,但前一对重要程度较高,在所有同层指标之间企业利润增长率重要程度最低.
被调查者完成同层指标(目标)之间相对重要程度选择后,系统将自动计算相对权重.这样就允许以最简单的方式定性地模糊输入相对权重.
2)调整级差 .如图2所示,重要程度等级左侧的滚动按钮可调整级差,将影响系统计算的相对权重值,并实时显示在窗口右侧,从而允许定量地、相对精准地修改权重值.
1.3 权重计算原理
评估系统用层次分析法[2]计算权重.先将评估指标zi与zj两两比较,计算出它们之间的级差,zi与zj的级差记为Δij.若两指标同等重要或者i=j,就令Δij=1;若zi不如zj重要,就令Δij=1/|Δij|.求出所有级差后可建立评判矩阵J:

比如,式(1)中Δ11=Δ22=…=Δ55=1,Δ24=Δ42=1,Δ13=3,Δ31=1/3,等等.
判断矩阵J的特征向量V的各分量可由式(1)求得:

按式(3)对V进行归一化处理,然后可求得指标的相对权重qi,如式(4).

2 权重样本与期望
测评指标的权重主要来源于调查统计.将来自于同一个群体的一批调查值称为样本,记为Q,另记Q的算术平均值为.样本可用集合表示:
Q={qi|1≤qi≤n,n为样本数量}
实践中发现多数权重样本基本服从正态分布,但单偏型样本的比例也很高.图3是“企业利润增长率”权重调查的一个样本(x-y散点图),可知多数权重值分布在7.69%~14.29%之间.其原因是多数人理解、认同两型化及和谐社会的要求,将该指标的级次设置为最低(或并列最低),参见图2.但也存在设置级次最高的情况,致使最大值达34.06%,可能源于认识误区或者随意操作等原因.该样本平均值为=15.07%,两侧占比分别为1/3和2/3,明显偏向一侧故不属于正态分布.

图3 单偏型样本分布图Fig.3 Single-sample bias based on weighing
实践中发现,若某评测指标明显重要(或不重要),其样本大多单偏,且容易出现极端情况.在权重调查中这种现象较为普遍.
若以算术平均值¯Q作为调查结果(即样本的期望值),上述样本中有2/3的人认为权重应低于¯Q,故显然不合适.项目组研究认为:
1)样本期望值应能反映多数人意愿,所以应靠近样本中点(即两侧占比相同,图3中是0.120 6),因此需对样本适度纠偏;
2)期望值应尊重每一位参与者——保持样本偏向不变.样本偏向可能代表了被调查者的行业利益诉求,因此纠偏需适度;
3)期望值应从剔除极端偏离值后的样本中求取.在明显重要(或不重要)的评测指标的权重样本中,极端偏离值可能来自于操作失误或认识误区.
3 权重回归算法
从权重样本中求期望值称为权重回归,项目组设计的权重回归算法如下:
1)记N为样本Q中的权重值个数,令X=1/N,另记为样本中点.
2)计算样本均值,按下式计算μ:
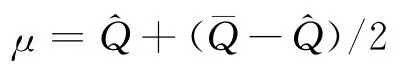
按下式计算样本均方差σ2:

3)视样本为正态分布Q~N(μ,σ2),其累积分布函数f(x)如下:

4)令f(xlow)=X,f(xheight)=1-X,并调整X的值:X←0.5X.
5)在样本Q中剔除Q′:

若Q′为空,则以μ为样本期望值结束算法,否则转2).
上述算法的目的是寻找合适的正态分布(比照该正态分布被更新的样本中没有小概率事件),并以其均值作为样本期望值.
以2)中计算的μ为均值建立正态分布,是为了使之靠近样本初始态的中点.
样本的第一次更新是剔除两侧样本中概率(X=1/N)大于正态分布概率的权重值,这种粗犷的剔除是为了去除极端偏离值;第二次更新时,重建正态分布并剔除样本中概率2倍于(X←0.5X)正态分布概率的值,它们是小概率事件不应出现在样本中;第三次更新剔除4倍于正态分布概率的值;……按几何级数递增严格小概率事件定义是为了纠偏适度——加速循环终止以保持样本偏向.
若样本足够大且初始态是正态分布,回归算法求得的期望值显然与算术平均一致.实践表明,样本单偏越严重回归算法纠偏越多,反之亦然.
如图3的权重样本的中点是=0.120 3,均值为=15.07%,均值两侧占比为66.7%对33.3%.运用回归算法处理该样本共循环三次,获得的期望值为=0.132 8,两侧占比为59%对41%.
4 权重分配策略
实践表明,在权重录入工具中预设参照值(包括等级和级差,参见图2)可使调查样本更趋于正态分布,权重期望值更趋于合理.
权重调查需针对不同群体,如政策相关人员、企业及公众等.记q0为项目组集体讨论确定的权重,反映科学发展观、新型工业化、两型化社会等理论要求.记q1为以q0为参照值向政策相关人员调查统计获得的权重.记q2,q3为以q1为参照值向本地区装备制造企业及公众分别调查统计获得的权重.那么评测指标的权重可表示为:
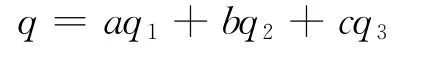
评估系统目前的权重分配系数为:

实践表明,在权重录入工具中预设参照值(包括等级和级差,参见图2)可使调查样本更趋于正态分布,权重期望值更趋于合理.
5 绿色度评估思路
企业的绿色度用绿色星级来衡量,创办一种称之“绿色银行”的评估机构,创建一种称之“绿色币”的尺度及其信贷制度[1-2].“绿色银行”采用评估体系,定时对企业进行绿色度评估,定时公布企业“绿色币”的数量,并根据企业“绿色币”的多少评定企业的绿色星级,还根据存欠“绿色币”的多少实行“息上加息”的信贷制度.
绿色度评估的技术流程如图4所示,在政府倡导和要求之下,通过评估专家分析、相关部门指导、公众调查统计等方式共同研究出各类行业测评指标与权重等标准,在“绿色银行”的指导之下,各企业根据标准首先进行自评,然后由“绿色银行”正式评定绿色星级.政府部门根据评定结果给企业授牌,或对企业进行相应的奖罚处理,并且将评定结果作为是否继续支持、评优、评先等一系列问题的依据.

图4 绿色度评估的技术流程Fig.4 Technical processes of green-degree assessment
6 结束语
研究建立装备制造业资源环境与可持续发展的综合评价体系是实现装备制造业可持续发展的重要举措,可以借此强化装备制造企业可持续发展意识,影响其对于资源环境的利用,规范企业行为,作为政府制定政策、配置资源、调整产业结构、投入资金等方面的依据,解决社会可持续发展要求与装备制造企业追求经济利益间的冲突,把建设“绿色制造”战略落到实处,从源头上推进装备制造业可持续发展.
[1] 尹望吾,杨义蛟,庞小兵.装备制造企业绿色星级评估方法研究[J].科技通报,2009,25(4):524-529.YIN Wang-wu,YANG Yi-jiao,PANG Xiao-bing.The research of green star-enterprise evaluation for equipment industry[J].Bulletin of Science and Technology,2009,25(4):524-529.(In Chinese)
[2] 杨义蛟,尹望吾,谭青.装备制造业可持续发展的模糊综合评价[J].制造业自动化,2009,31(7):4-9.YANG Yi-jiao,YIN Wang-wu,TAN Qing.Fuzzy comprehensive evaluation of equipment industry sustainable development[J].Manufacturing Automation,2009,31(7):4-9.(In Chinese)
[3] 王贤琳,张华,宋佳佳.绿色制造技术标准体系研究[J].标准科学,2009(9):9-13.WANG Xian-lin,ZHANG Hua,SONG Jia-jia.Research on standard system of green manufacturing technology[J] .Standard Science,2009(9):9-13.(In Chinese)
[4] ZHOU Chang-hun,YIN Guo-fu,HU Xiao-bing,etal.Multi objective optimization decision making of material selection oriented to green design[J].Computer Integrated Manufacturing Systerms,2008,12(5):1023-1028.
[5] YIN Wang-wu.The study on green design of industrial products and circular economy[C]//Proceedings of the 2006International Conferences Industrial Design.Beijing:China Machine Press,2006:489-491.
[6] 刘晓洁,沈镭.资源节约型社会综合评价指标体系研究[J].自然资源学报,2006,21(3):382-391.LIU Xiao-jie,SHEN Lei.Resource-saving society of comprehensive evaluation index system [J].Natural Resources,2006,21(3):382-391.(In Chinese)
[7] 李崧,邱微,赵庆良,等 .层次分析法应用黑龙江省生态环境质量评价研究[J].环境科学,2006,27(5):1031-1034.LI Song,QIU Wei,ZHAO Qing-liang,etal.Applying analytical hierarchy process to assess ECO environment quality of heilongjiang province[J].Environmental Science,2006,27(5):1031-1034.(In Chinese)
[8] 张艳,贾海霞.企业“绿色度”的模糊评价模型与应用[J].环境科学与管理,2005,30(3):104-106.ZHANG Yan,JIA Hai-xia.On fuzzy assessment and application of enterprises green degree[J].Enviromental Science and Management,2005,30(3):104-106.(In Chinese)

