兆瓦级风电偏航减速机行星齿轮疲劳仿真分析*
鄂加强,李光明,张 彬,董江东,朱 浩
(湖南大学 机械与运载工程学院,湖南 长沙 410082)
对于将风能转化为电能的兆瓦级风力发电机组来说,其关键部件之一的偏航减速器用来调整风力发电机机头的转向以便获得最大的风力来源,其传动比大,传递扭矩大,工作环境恶劣,要求可靠性高、寿命长.而兆瓦级风电偏航减速机行星齿轮则是实现偏航减速功能的主要零件,其材料的疲劳问题经常出现.
由于兆瓦级风电偏航减速机行星齿轮形状比较复杂,传统的齿轮接触强度计算均是以赫兹公式为基础,通过对原始的赫兹公式加以变形及系数修正来获得的,难以精确地求解出齿轮的接触强度,因此采用传统的计算方法不能确定兆瓦级风电偏航减速机行星齿轮真实的应力及变形分布规律.近年来,应用新的计算软件和3D建模技术[1-2]进行风电机组的仿真分析已成为有效的设计方式.目前国内外针对齿轮疲劳破坏中出现几率最高的齿面接触疲劳强度问题[3-5]则普遍采用ANSYS软件进行疲劳寿命的总体预测和较准确的应力变形分析[6],可为齿轮的疲劳寿命计算提供完整的应力-时间历程曲线,并且能够进行齿轮的动态疲劳寿命计算.
为此,本文应用ANSYS软件建立兆瓦级风电偏航减速机行星齿轮的研究模型,进行偏航驱动减速机中行星齿轮和太阳轮啮合的应力分析及疲劳分析,并从弹性力学出发,用现代设计方法研究兆瓦级风电偏航减速机行星齿轮的受载变形情况和接触强度,通过接触疲劳试验计算分析找出点蚀的影响因素,其研究结果对兆瓦级风电偏航减速机行星齿轮质量、性能及寿命的提高具有重要的意义.
1 兆瓦级风电偏航减速机行星齿轮接触数值计算
根据其几何特征和主要力学特性,选用兆瓦级风电偏航减速机行星齿轮中的太阳轮和行星齿轮的啮合作为分析对象.兆瓦级风电偏航减速机行星齿轮接触界面非线性主要来源于:1)接触界面的区域大小和相互位置以及接触状态不仅事先都是未知的,而且是随时间变化的,需要在求解过程中确定.2)接触条件的非线性.接触条件的内容包括:①接触物体不可相互侵入;②接触力的法向分量只能是压力;③切向接触的摩擦条件.
这些条件区别于一般约束条件,带有强烈的非线性.因此,采用对称罚函数法进行兆瓦级风电偏航减速机行星齿轮接触数值分析.
1.1 兆瓦级风电偏航减速机行星齿轮接触数值计算条件
1)接触界面与非嵌入条件.考虑两齿轮A与B的接触问题,其现时构形分别为VA和VB,边界面分别为AA和BB,接触面记为AC=AA∩AB,如图1所示.
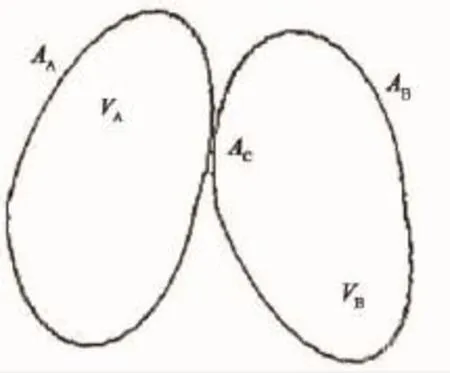
图1 两物体接触示意图Fig.1 Schematic diagram of the two objects in contact
太阳轮A为主体(Master),其接触面为主动面,行星齿轮B为从体(Slave),其接触面为从动面.A与B接触时的非嵌入条件可以表示为:

式(1)说明,太阳轮A与行星齿轮B不能互相重叠,由于事先无法确定两齿轮在哪一点接触,因此大变形问题中无法将非嵌入条件表示成位移的代数或微分方程,只能在每一时间步对比AC面上齿轮A与B对应节点的坐标,或对比速率来实现位移协调条件:
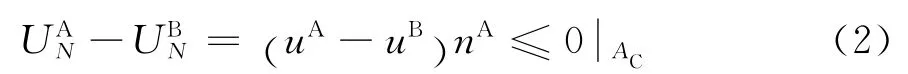
或
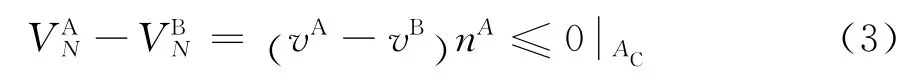
式中下标N表示接触法向.
2)接触界面力条件.由牛顿第三定律,接触面力应满足:

式中tNA与tBN分别为齿轮 A 与B的法向接触力;tTA与tTB分别为齿轮A与B的切向接触力.
1.2 兆瓦级风电偏航减速机行星齿轮接触问题有限元数值计算方法
兆瓦级风电偏航减速机行星齿轮接触数值计算的实现过程如下:
1)如图2(a)所示,在齿轮碰撞体中选取任意一从节点nS,搜索与其最靠近的主节点mS.
2)检查与主节点mS有关的所有主单元面,确定从节点nS穿透主表面时可能接触的主单元表面,如图2(b)所示.若主节点mS与从节点nS不重合,当满足不等式(5)时,从节点nS与主单元面Si接触.

式中Ci和Ci+1是主单元面上在mS点的两条边矢量;矢量S是矢量g在主单元面上的投影;g为主节点mS指向从节点nS的矢量,如式(6)所示:
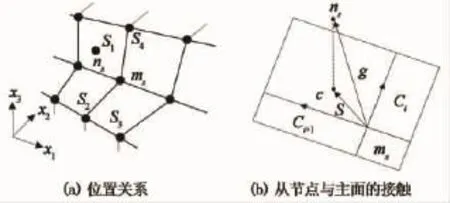
图2 从节点与主面接触示意图Fig.2 Schematic diagram of the from node and the main surface in contact
对于主单元面Si,则式(6)中m如式(7)所示:

如果nS接近或位于两个主单元面的交线上,式(5)可能不确定.在这种情况下,若nS位于两个主单元面的交线上,则S取极大值,即
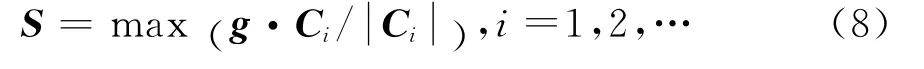
3)确定从节点nS在主单元面Si上的接触点c的位置.主单元面Si上任一点位置矢量如式(9)所示:
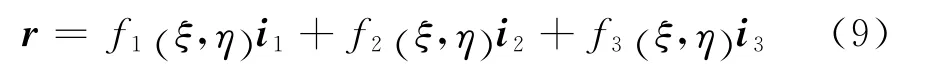
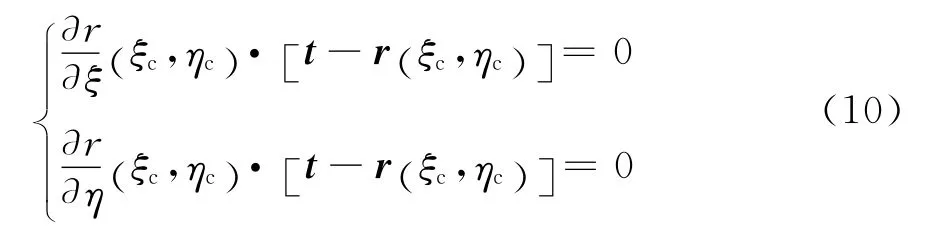
式中t为主单元面Si上不同于矢量r的任意矢量.
4)检查从节点是否穿透主面.若l=ni[tr(ξc,ηc)]<0成立,则表示从节点nS穿透含有接触点c(ξc,ηc)的主单元面Si;其中ni是接触点处主单元面的外法线单位矢量如式(11)所示:
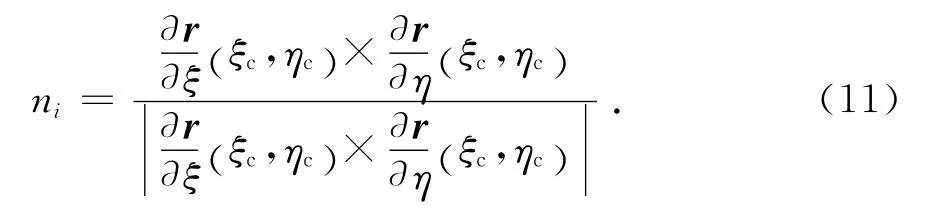
若l≥0,则表示从节点ni没有穿透主单元面,即两齿轮没有发生碰撞-接触,不做任何处理,从节点ni处理结束,开始搜索下一个从节点ni+1.从节点与主单元面的关系如图3所示.

图3 从节点与主单元面的关系图Fig.3 Diagram of the from node and the main unit plane
5)若从节点穿透主面,则在从节点nS和接触点c之间施加法向接触力为:

式中ki为主单元面的刚度因子,可用式(13)表示:

式中Ki为接触单元的体模量;Ai为主单元面面积;Vi为主单元体积;Li为板壳单元最大对角线长度;f为接触刚度比例因子.f取值过大时,可能导致数值计算的不稳定,除非缩短时间步长.
在从节点nS上附加法向接触力矢量fS,再根据牛顿第三定律,在主单元面的接触点c上作用一个反方向的力——fS,按照式(14)将c点的接触力等效分配到主单元面Si的4个主节点上,记为fjm,j=1,2,3,4(单元第j个节点),则
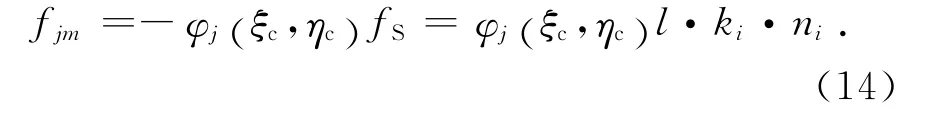
式中φj(ξc,ηc)为主单元面上的二维形函数,且在接触点c有∑φj(ξc,ηc)=1.
6)摩擦力计算.从节点nS的法向接触力为fS,则它的最大摩擦力为FY=μ|fS|,μ为摩擦因数.设在上一时刻tn从节点nS的摩擦力为Fn,则当前时刻tn+1可能产生的摩擦力(试探摩擦力)F*=Fn-kΔe,k为界面刚度,当前时刻tn+1的摩擦力Fn+1由式(15)确定:

按照作用力与反作用力原理,计算主单元面上4个主节点的摩擦力.若静摩擦因数为μS,动摩擦因数为μd,用指数插值函数来使两者平滑过渡,如式(16)所示:
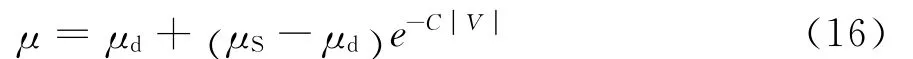
式中V=Δe/Δt,Δt为时间步长;C为衰减因子.
7)将接触力矢量fS,fjm(j=1,2,3,4)和摩擦力矢量投影到总体坐标轴方向,得到节点力总坐标方向向量,组集到总体载荷矢量Pf中,进行动力学分析.
为了验证下面数值有限元分析计算结果的可靠性,同时节省实验时间与费用,本文对行星齿轮和太阳轮的初始接触应力进行了理论估算.
齿面接触应力的计算是以两圆柱体接触时的最大接触应力推导出来的.接触区的最大接触应力σH可根据弹性力学中的知识计算:

式中b为配对齿轮的宽度,mm;Fn为配对齿轮接触面的法向力,N;ZE为配对齿轮的材料系数,满足:,其中μ1,μ2为配对齿轮材料的泊松比,E1,E2分别为两齿轮材料的弹性模量,MPa;ρ为综合曲率半径,ρ=ρ1ρ2/(ρ1+ρ2),ρ1,ρ2为两圆柱体接触处的曲率半径,±号分别表示外接触或内接触.
根据湖南某机械公司提供的各个参数,计算转速在1 000r/min,初始最大接触应力为:σH=405.63MPa.
2 兆瓦级风电偏航减速机行星齿轮接触数值仿真分析
2.1 兆瓦级风电偏航减速机行星齿轮接触数值仿真模型建立
兆瓦级风电偏航驱动减速机整体装配模型和一级行星传动部分的装配模型如图4所示.其材料属性中的泊松比为0.3,内径D1=66mm,外径D2=78.5mm,厚度为H=40mm,其他材料属性见表1和表2.
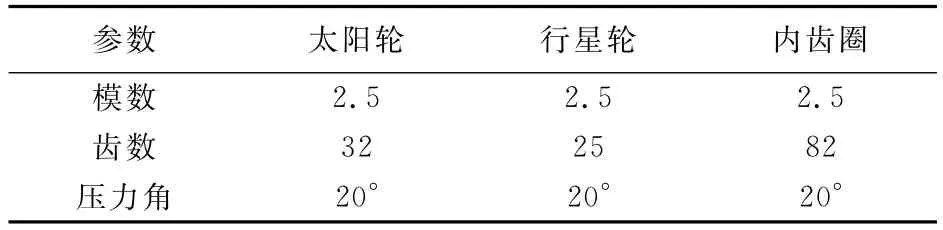
表1 各齿轮基本参数Tab.1 The gears basic parameters

表2 齿轮材料属性Tab.2 The gears material attribute

图4 兆瓦级风电偏航驱动减速机虚拟模型Fig.4 The virtual model of MW wind power yaw reducer
考虑到直齿齿轮可转化为平面问题,故选用二维4节点板单元PLANE42建立太阳轮和行星齿轮面模型.为避免可能出现应力集中的区域及应力梯度高的区域应布置较密的网格,在应力变化平缓的区域,布置较稀疏的网格,得到如图5所示兆瓦级风电偏航驱动减速机接触应力分析网格.

图5 二维行星齿轮网格划分Fig.5 Meshing of two-dimensional planetary gear
2.2 兆瓦级风电偏航减速机行星齿轮接触有限元结果分析
根据兆瓦级风电偏航减速机的设计要求,额定输入功率为3.5kW,额定输入转速为1 000r/min(6 000°/s),总减速比为1 150.由转矩公式T=9.55×106×P/N,其中P为功率(kW),N为转速(r/min),T为转矩或扭矩(N·mm),得减速机的输出转速为0.87r/min(5.2°/s),额定输入转矩为33 425N·mm.
兆瓦级风电偏航减速机行星齿轮接触有限元计算结束后,兆瓦级风电偏航减速机行星齿轮接触变形分布、接触节点位移分布、行星齿轮啮合过程的接触应力分布和行星齿轮啮合过程的等效应力分布如图6所示.
图6(a)和 (b)表明,兆瓦级风电偏航减速机行星齿轮初始啮合接触时,挤压产生应力,此时应力最大值主要集中在行星齿轮的齿顶一侧,接触点上的最大接触应力为395MPa,而传统计算值为405.63 MPa,误差在5%的范围内,考虑到传统计算在计算系数的选取过程中会带来的一定误差,故兆瓦级风电偏航减速机行星齿轮接触模拟结果较为可信.
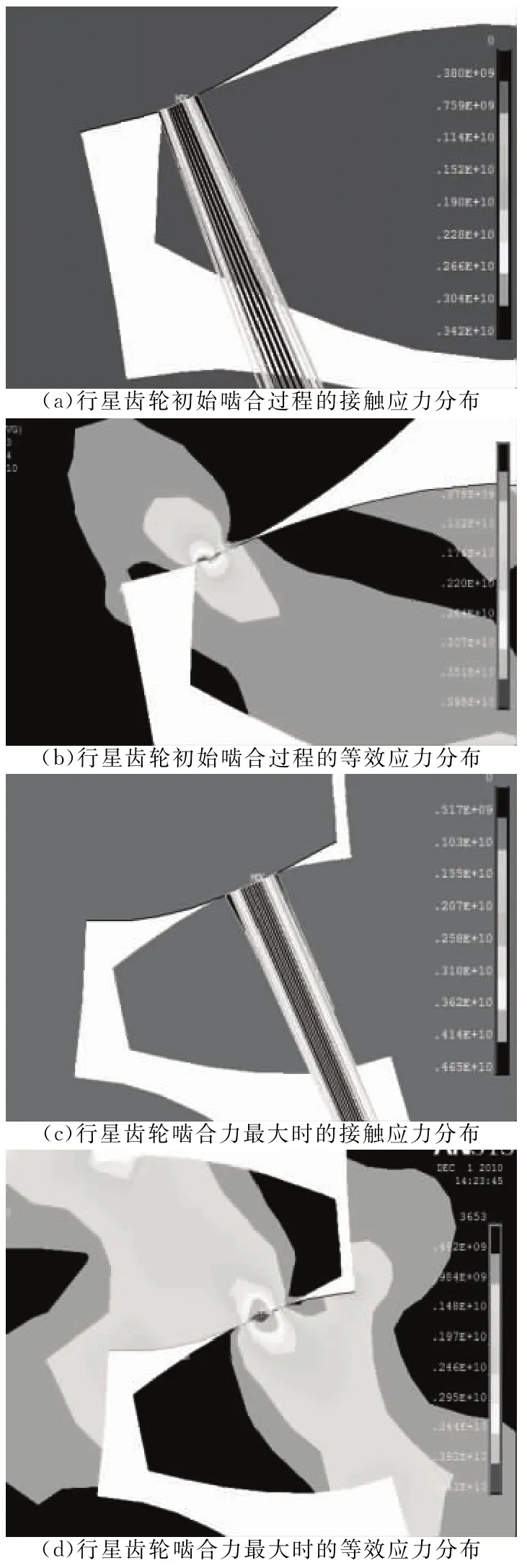
图6 兆瓦级风电偏航减速机行星齿轮接触有限元计算结果Fig.6 Finite element simulation results of MW wind power yaw planetary gear reducer’s contact
图6(c)和(d)表明,随着行星齿轮啮合的继续进行,产生接触应力的范围不断扩大,此时最大应力急速增大至460MPa以上,小于行星齿轮材料的屈服极限.在应力集中部分将不会产生塑性流动及引发行星齿轮齿面塑性变形.
3 行星齿轮疲劳分析
在交变载荷重复作用下,材料或结构仍然会发生疲劳破坏,风力发电设备要求其运行寿命较长,因而其疲劳分析显得尤为重要.
根据齿轮啮合原理,齿轮在传动过程中,轮齿受到脉动载荷的作用,即当轮齿进入到啮合状态时,轮齿要受到载荷的作用,而轮齿一旦脱离啮合,受到的载荷则变为零.因此,轮齿的接触应力为交变应力.根据以上获得的接触应力值,利用ANSYS的疲劳分析计算模块对其进行接触疲劳寿命分析.为此,选择产生最大接触应力的节点为分析点,因为疲劳裂纹往往容易先在此处萌生.疲劳分析还需疲劳特性参数即S-N曲线[7-9].
在齿轮疲劳试验中用疲劳曲线 (S-N或R-S-N或C-R-S-N)表征疲劳破坏的应力S和疲劳寿命N之间的关系.接触应力的分析和计算目前一般仍采用赫兹公式或者是赫兹公式的修正公式[10],但应考虑到切向载荷等影响,并且接触应力应该计算齿面抗点蚀能力最弱的危险点处的应力.
S-N曲线是根据数理统计方法,对预先设计好的在不同应力水平下获得的适当数量试件的试验数据进行处理后得出的,表示应力与寿命的关系.
如图7所示,S-N曲线由水平段和倾斜段组成,其左侧倾斜段表示有限循环次数下的极限应力,称为条件疲劳极限;右侧水平段表示持久疲劳极限,曲线的拐点对应的应力总循环次数称为循环基数N0.

图7 材料S-N曲线Fig.7 TheS-Ndiagram of the material
疲劳寿命试验中倾斜段的应力与寿命的关系通常具有如下的幂函数形式[11-15]:

式中S为极限接触应力(即将要发生扩展性点蚀时的最大接触应力);S0为常数,可近似代表疲劳极限;N为S对应的应力总循环次数;m为指数;C为常数.
当S0=0时,式(18)就变成二参数的幂函数形式,称为Basquin公式.将式(17)两边取对数,得
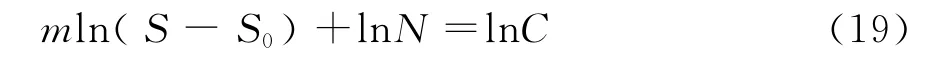
令X=ln(S-S0),Y=lnN,a=lnC,b=-m,则有

采用如表3所示的42CrMo材料特性参数对齿轮进行S-N曲线分析.
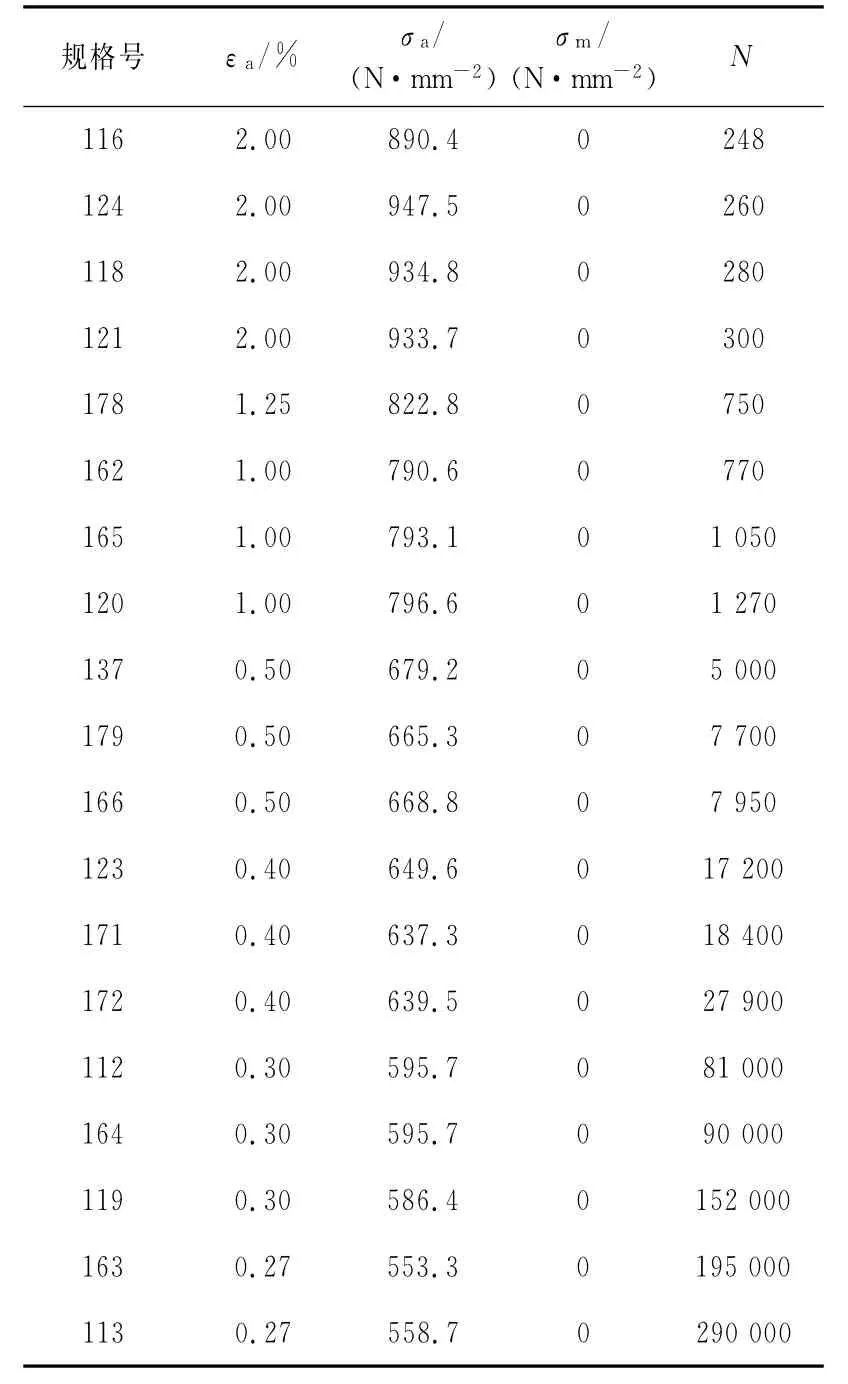
表3 42CrMo材料特性参数Tab.3 42CrMo material parameters
选择产生最大接触应力的节点为分析点,因为疲劳裂纹往往容易先在此处萌生.打开ANSYS的后处理器,打开S-NTable命令 Main Menu/General Postproc/Fatigue/Property Table/S-N Table,进入“S-N表”对话框,将其输入,如图8所示,然后由坐标值得到节点号:Utility Menu/Parameters/Scalar Parameters.再指定最大接触应力位置,从数据库中提取应力值,保存好应力值后,设置好事件的重复次数,最后进行疲劳计算:Main Menu/General Postproc/Fatigue/Calculate Fatig.经过疲劳寿命分析计算,可以得出的疲劳分析结果文件,从结果文件可以看出,计算所得出的该材料齿轮轮齿的疲劳寿命为125 800次,累计疲劳系数为0.725 01.显然,其抗疲劳性能较好,能满足兆瓦级风电偏航减速机行星齿轮设计与运行要求.

图8 疲劳S-NTable对话框Fig.8 Dialog box of fatigueS-Ntable
4 结 语
1)本文先用Pro/E和ANSYS软件对总体偏航减速机进行了装配和仿真分析,得到了动力学仿真分析结果图(图4),验证了整个偏航减速机的模拟运行良好,为下一步运用ANSYS软件进行接触和疲劳分析打下了良好的基础.
2)采用ANSYS有限元技术对行星齿轮接触问题进行分析,得到了齿轮啮合过程的接触应力分布和等效应力云图(图6),从图中可以看出行星齿轮初始啮合接触时,挤压产生的应力值,此时应力最大值主要集中在行星齿轮的齿顶一侧,接触点上的最大接触应力为395MPa,并随着行星齿轮啮合的继续进行,产生接触应力的范围不断扩大,此时最大应力急速增大至460MPa以上,略小于行星齿轮材料的屈服极限.故兆瓦级风电偏航减速机行星齿轮接触模拟结果较为可信,有助于优化行星齿轮的设计.
3)通过有限元法对行星齿轮进行了疲劳仿真分析,获得了行星齿轮的疲劳寿命次数为125 800次和累计疲劳系数为0.725 01.从计算结果可以看出,以42CrMo为材料的行星齿轮在一定转矩下的抗疲劳特性符合工业设计的要求,验证了研究机理是切实可行的.对行星齿轮的疲劳寿命和可靠性的确定有一定价值,对提高齿轮的设计质量,降低设计费用,缩短开发周期,具有实际意义.
[1] GAO S,BUI T D.Image segmentation and selective smoothing by using mumford-shah model[J].IEEE Transactions on Image Processing,2005,14(10):1537-1549.
[2] LITVIN R L,VECCHIATO D,DEMENEGO A.Design of one stage planetary gear train with improved conditions of load distribution and reduced transmission errors[J].Mechanical Design,2002,124(4):745-752.
[3] YE Zhi-quan,MA Hao-min,BAO Neng-sheng.Structure dynamic analysis of a horizontal axis wind turbine system using a modal analysis method[J].Wind Engineering,2001,25(4):237-248.
[4] BENTKUS V,ZUIJLEN M V.On conservative confidence intervals[J].Lithuanian Mathematical Journal,2003,43(2):141-160.
[5] JUNIOR R C S F,NETO A D D,AQUINO E M F D.Building of constant life diagrams of fatigue using artificial neural networks[J].International Journal of Fatigue,2005,27(7):746-751.
[6] GLODEZ S,ZRAML M,KRAMBERGER J.A computational model for determination of service life of gears[J].International Journal of Fatigue,2002,24(10):1013-1020.
[7] KAHRAMAN A,VIJAYAKAR S.Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set[J].Journal of Mechanical Design,2001,123(3):408-415.
[8] KIM D H.Random fatigue analysis of automotive bevel gear[J].Key Engineering Materials,2006,326/328(2):987-990.
[9] HAIBA M,BARTON D C,BROOKS P C,etal.Review of life assessment teehniques applied to dynamically loaded automotive components[J].Computers &Structures,2002,80(5/6):481-494.
[10] MULLER S,DEICKE M,DE DONCKER R W.Doubly fed induction generator systems for wind turbines[J].Industry Applications Magazine,IEEE,2002,8(3):26-33.
[11] PAVLOV N V,TESKIN O I,UKOLOV S N.Comparison of some methods of calculating the confidence bounds for the reliability index of a system from the results of testing its components[J].Journal of Mathematical Sciences,2001,103(5):578-581.
[12] SENTHILVEL Vellaiehamy.Transient dynamic fatigue analysis of automotive structures using proving ground road profiles[C]//SAE Paper.2005-01-0514.
[13] BROUGHTON Howard,SIMS J J.High-speed gear-failure digital video imaging system[C]//PAISLIV D L,FRANK A.Proceedings of 22nd International Congress on High-Speed Photography and Photonics.Santa Fe,NM,USA:The International Society for Optics and Photonics,2005:1013-1016.
[14] YIN Chun-gen,LUO Zhong-yang,ZHOU Jun-hu,etal.A novel non-linear programming-based coal blending technology for power plants[J].Chemical Engineering Research and Design,2000,78(1):118-124.
[15] 李光明 .风电偏航驱动减速机抗疲劳机理研究[D].长沙:湖南大学机械与运载工程学院,2011.LI Guang-ming.Study on anti-fatigue mechanism of planetary gear for megawatt wind power yaw reducer[D].Changsha:College of Mechanical and Vehicle Engineering,Hunan University,2011.(In Chinese)

