M2M小数据业务的IEEE 802.11WLAN分析模型
王雅辉,迟学芬
(吉林大学 通信工程学院,吉林 长春 130012)
1 引言
物联网就是把世界上所有的机器都连接到一张通信网中,使所有的机器都具备联网和通信的能力,M2M 是物联网当前最普遍的应用形式[1,2]。M2M 的通信需要多种网络的支撑,包括 GSM、CDMA、TD-SCDMA等蜂窝网络,WLAN、WPAN等专用无线网络以及 Internet等各种网络[3]。由于WLAN具有中小范围覆盖和高速率接入等显著优势,3GPP及3GPP2等组织皆考虑了WLAN与第三代移动通信的融合问题,既能弥补移动业务中速率的不足,又能提高业务移动性和覆盖面。运营商所建设的以3G为主体、以WLAN为重要补充的无线宽带数据网将成为M2M通信的最佳承载平台。
目前,国内外对M2M的学术研究尚处于起步阶段,有限的研究结果主要集中于M2M基本应用问题,如市场预测、支撑平台、业务管理、终端模块等[4]。对 M2M 业务数学建模和基于特定网络模型(如WLAN)性能评价的研究报道几乎是空白。3GPP定义了7类35种M2M业务,本文研究最典型、也是最重要的一类M2M业务——小数据(small data)业务,其基本特点为具有巨大的随机业务数量、每次通信数据量小,且具有时延容忍、耐性重试特性。本文基于排队理论,针对IEEE 802.11,建立M2M小数据业务的网络分析模型,基于业务特性优化WLAN。
在基于排队理论的 WLAN研究领域,研究成果集中于WLAN服务时间建模和WLAN的系统性能分析。Bianchi提出的二维马尔可夫链模型广泛应用于关于IEEE 802.11协议DCF (distributed coordination function) 的性能分析中,但是这个分析模型存在一些明显的缺陷[5],后来很多文献对DCF做了深入的研究,改进了Bianchi的模型。ZA推导了一个饱和时延,考虑了信道忙时退避计数器停止[6];H.Wu提出了限制发送失败后的重发次数[7];Z.H.Velkov分析了信道有误码的情况[8];有的文献还研究了吞吐量极限,指出了隐藏终端的影响等。真实的网络状况一般是非饱和的,有些文章将Bianchi的饱和模型直接扩展到非饱和情况,增加了一个或多个“空闲”状态来代表没有数据帧要发送的情况,分析网络的非饱和程度对吞吐量的影响。为了提供准确的时延分析,很多学者研究了 DCF的排队行为。Liu等将队列长度作为一个新维度,建立了3-D Markov链模型研究DCF性能,模型较复杂[9]。还有一种方法是把 DCF描述为封闭的排队网络,将每个退避级数作为其中的一个 G/G/∞队列[10,11]。更多的研究成果是基于 Bianchi的排队理论分析系统,如用M/G/1建模WLAN[12]。后来,Vardakas用ON_OFF模型代替Poisson分布描述数据到达过程,表征业务的突发性[13]。基于G/G/1的队列模型,由于计算复杂,依赖于几个近似参数,导致分析结果与仿真比较有很大差别[14]。考虑到实际系统容量有限,有的研究用M/G/1/K排队系统建模WLAN,但是,他们没有考虑信道差错,而且,数据帧到达都是经典的Poisson过程[15,16]。
目前的研究都致力于更精确地建模和改善WLAN的DCF机制,而很少考虑针对业务的DCF优化问题;同时,为了简化排队系统求解,大多数研究采用了适合语音业务的经典的Poisson分布作为到达过程。当M2M业务大量应用于通信系统时,系统业务源将呈现强烈异构特性,因此,研究面向业务的机制优化具有重要意义。
根据M2M的小数据业务的时延容忍、耐性重试特性,本文提出了一种大时间尺度退避机制,用二项式分布取代均匀分布,用二维马尔科夫链建模了具有大时间尺度退避机制的802.11服务过程,推导了服务时间的概率分布。同时,通过参数控制,实现了退避机制的网络自适应特性。针对 WLAN的非理想信道和非饱和状态,提出了IPP/G/1/K的离散时间排队模型。IPP (interrupted poisson process)的多态特性适于描述M2M小数据业务的突发性,同时IPP融合了到达的概率分布和时间特性。通过求解IPP/G/1/K排队系统,得到M2M业务的吞吐量、时延等QoS参量。算法仿真实验结果表明,本文提出的大时间尺度退避机制,优化了802.11的性能,缓解了大量M2M小数据业务引起的冲突,增大了系统的吞吐量。
2 M2M小数据业务模型
机器类通信(MTC, machine type communication)业务的特性与传统的人与人通信 (H2H, human to human)业务的业务特性差异很大。M2M 业务类型繁多,不可能找到一个通用模型来描述所有 M2M业务。M2M 小数据业务特征可概括为低移动性、时间容忍、分组交换、小数据传输、大业务数量[17]。遥感勘测、自动售货机就是典型的M2M小数据业务。假定每个站点的 M2M小数据业务到达为 IPP过程。在 IPP过程中,ON状态时数据到达,OFF状态时,没有任何数据到达,它适合描述业务的突发性。IPP过程可以看作是二态 MMPP (Markov modulated poisson process)的一个特例,有转移概率矩阵R和到达概率矩阵Λ分别为
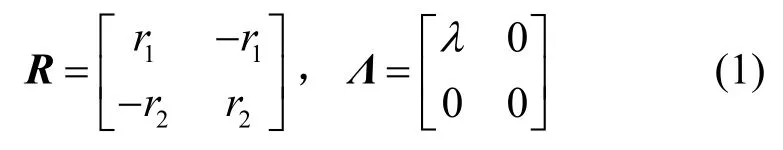
平稳概率分布
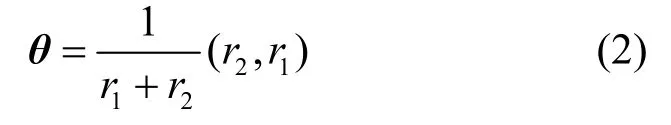
其中,r1和r2分别表示ON、OFF状态之间的转移速率;λ为ON状态时数据的到达速率。
3 IEEE 802.11MAC延时模型
IEEE 802.11无线局域网MAC层的DCF方式采用CSMA/CA机制。帧传输后,如果SIFS (short inter frame spacing)时间没有收到确认帧ACK,则认为此帧丢失或碰撞,于是这个帧就会按照二进制指数退避(BEB, binary exponential backoff)算法进行退避、重传。
将每个帧的发送过程建模为一个Markov链。帧离开站点的状态(例如成功发送或丢弃)是退避机制Markov链的吸收态。为了获得平均转变到吸收态的时间,应用一般状态转移图推导MAC层服务时间。
3.1 大时间尺度退避过程
在IEEE 802.11 DCF标准中,数据帧发生冲突后要按二进制指数退避算法退避,即竞争窗口乘2,然后从中以均匀分布随机选取一个值作为退避值。此算法在网络中活动STA (station)数量较少时的性能较好,因为竞争不激烈,并且竞争信道的退避等待时间较少;而当活动STA数量较大时,这种优势就会被因竞争信道发生冲突而重传浪费的信道资源所抵消,甚至被超过。
M2M 业务不同于具有用户主动权的 H2H业务,M2M 终端大多是可控的终端,而且很多业务对时延不敏感,当网络拥塞时可以多退避一段时间后再重试接入。本文考虑到M2M的这些特点,针对非实时小数据业务,提出大时间尺度随机退避的接入控制算法。算法的核心思想是优化 DCF退避机制,按更大的概率选取大的退避值,而不是以相等的概率均匀选择退避时间。这样以退避时间为代价来缓解站点的竞争碰撞。本文提出用二项式分布取代均匀分布,推导了二项式分布的系统接入过程,得到服务时间的概率分布。二项式分布的概率参数pb决定概率分布特性,为此,本文估计当前活动STA数量,动态调整pb,从而使算法具有网络自适应特性。
二项式(binomial)分布是一种离散型分布,概率公式为
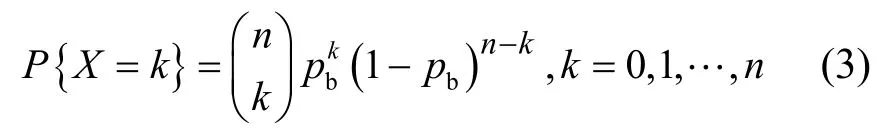
正好为二项式展开的各项,所以不难验证
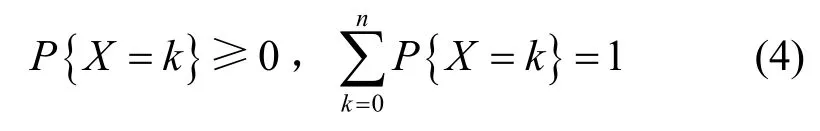
CSMA/CA退避算法的最小时间间隔为一个时隙σ。令s(t)表示在时隙t站点退避级数(0,1,…,α)的随机过程,其中α为重传限制次数,设最大退避级数为m,b(t)表示在时隙t站点的退避计时器取值(0,1,…,Wi-1)的统计过程。
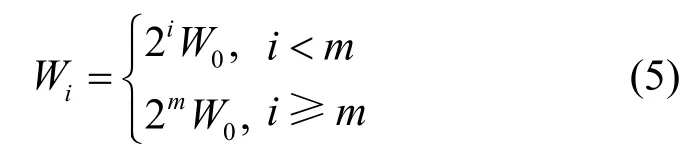
式(5)中,W0是初始竞争窗口,Wi是指退避级数为i时的竞争窗口大小。标准DCF算法中,b(t)是一个取值范围内的均匀分布,均值为。改用二项式分布,有:
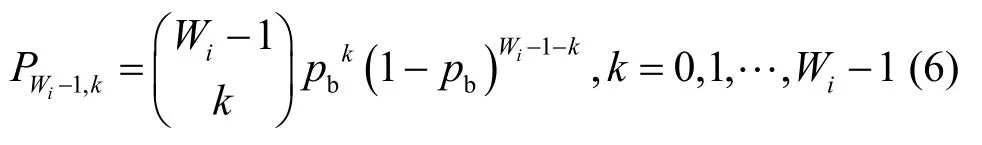
均值为(Wi- 1 )pb,当 pb>0.5时,二项式分布比均匀分布的退避时间均值要大,这也就是本文称其称为“大时间尺度”退避的原因。
由于b(t)、s(t)都取决于一个帧的传输历史以及曾经碰撞的次数,所以都不是Markov过程。但是,如果假设每一次试图发数据帧却失败的概率p恒定且相互独立,则{s(t), b(t)}是一个二维离散时间Markov链,如图1所示。
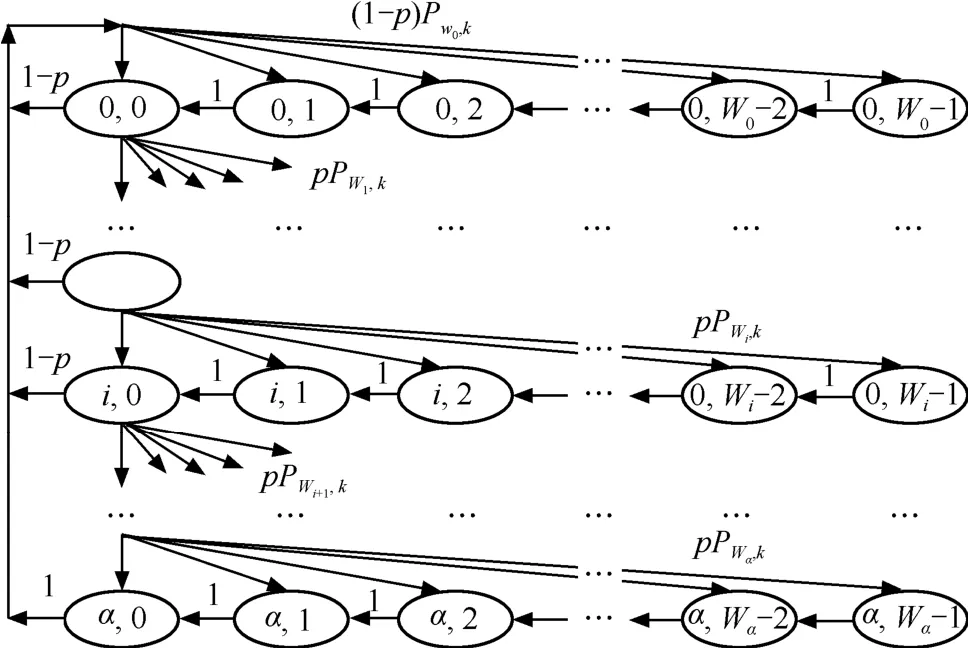
图1 Markov链状态转移图
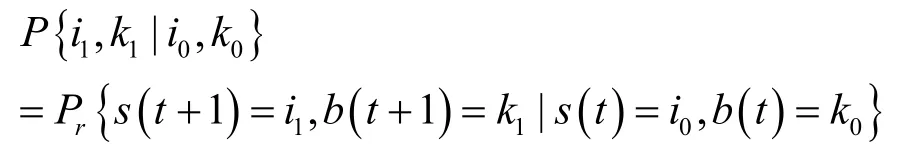
则图1的一步转移概率可以表示为
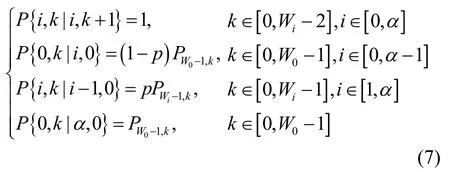
bi,k=Pr{ s( t)=i, b( t)=k},0≤i≤α,0≤k≤Wi为该Markov链的稳态分布,根据状态转移图,则有:
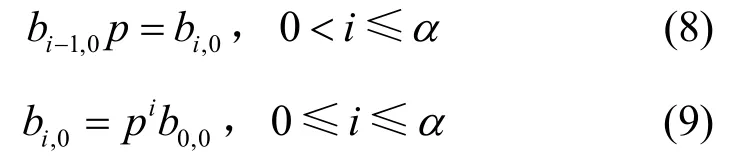
根据式(7)和式(9)可以表示为
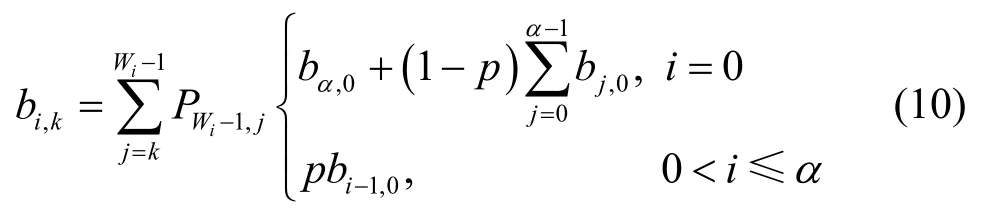
根据式(8)和式(10)可得:
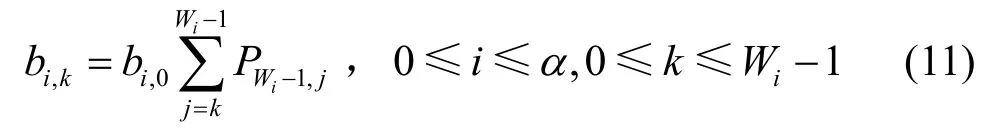
根据归一化条件可以推导出0,0b如式(12)所示。
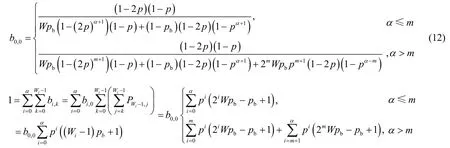
定义τ为站点在任一时隙发送数据帧的概率,则

最后τ变为式(14)。
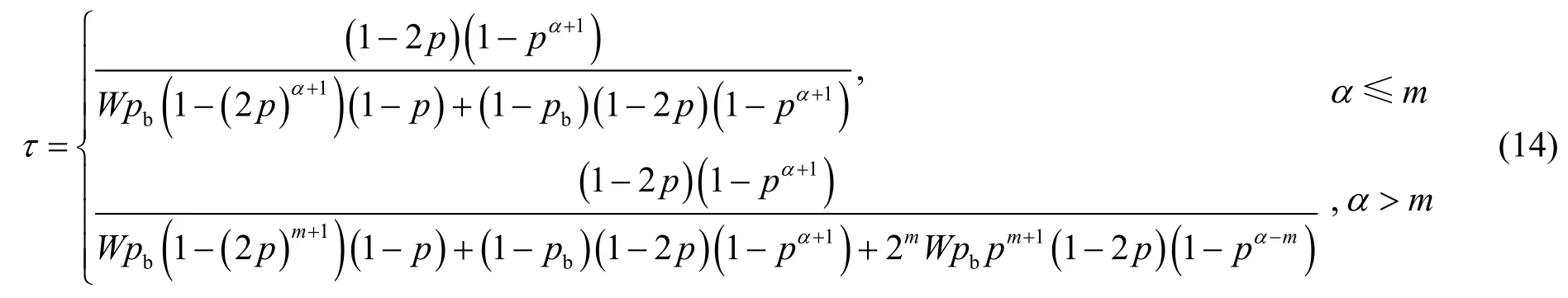
只有既没有碰撞也没有比特差错时,才能成功的传输一个帧,因此,计算p通过:
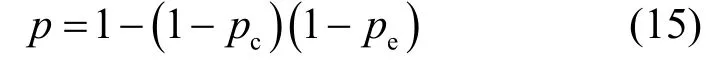
其中,pc为任一时隙发生碰撞的概率,pe为数据差错概率,它们的计算公式分别为
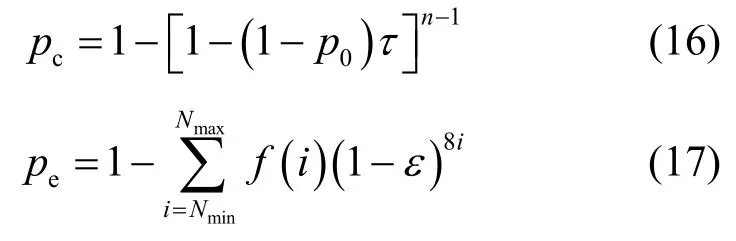
其中,p0是没有数据帧要发送的概率,ε是比特差错率,f(i)帧长度的概率分布,Nmin、Nmax分别是最小和最大帧长度,单位均为byte。通过联立式(14)和式(15),可以求出τ和p,进而可得到pc。如图2所示,碰撞概率pc和站点数量的关系,大尺度退避机制降低了系统碰撞率。二项分布概率pb越大,碰撞率越低,站点数量越多,效果越明显。

图2 数据发生碰撞的概率pc与站点数量的关系
3.2 碰撞和成功发送过程
令Ts表示成功传输数据帧所需的时间,Tc表示数据冲突持续的时间,DCF 2种接入方式下有不同的表达式[18]。
1) 基本机制
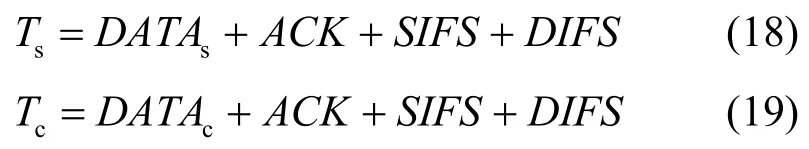
其中,DATAs、DATAc分别表示成功传输和碰撞的数据帧所需的时间,DIFS (distributed inter frame spacing)是DCF协议中使用的一种帧间间隔。等式中的参数均以时隙为单位,设传输最小、最大帧长度所占的时隙数分别为σmin、σmax。随机变量Ts的概率生成函数(PGF, probability generation function)为
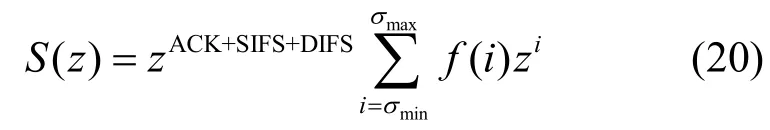
对于Tc,它是由最长的碰撞帧决定的。假定3个或更多帧同时碰撞的概率可以忽略,则
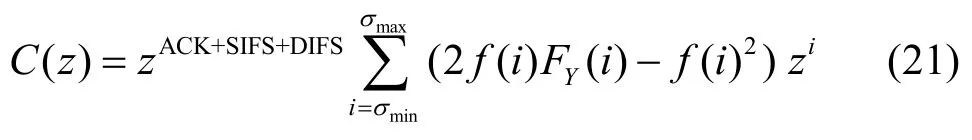
其中,FY(i)是f(i)的概率累积分布函数。
2) RTS/CTS机制
采用RTS/CTS (request to send/clear to send)接入方式能提高网络的吞吐率,降低冲突所浪费的时间,所以一般情况下,IEEE 802.11无线网络都会采用RTS/CTS方式。碰撞只会发生在RTS中,有:

显然,Tc是一个定值,它的PGF为
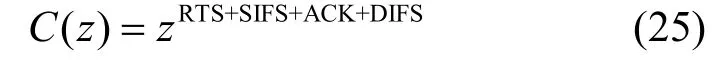
3.3 退避计时器递减过程
在退避过程中,如果信道空闲,退避计时器每隔一个空闲时隙就减 1。否则,当检测到一个正在进行的成功传输,退避计时器会被冻结一个 Ts时间;如果站点间有碰撞,会冻结Tc时间。
这里定义2个概率qt和qs,其中qt表示其他站点中至少有一个占用信道进行传输的概率,即在退避过程中检测到信道忙的概率;qs表示在考虑的时隙,当前站点没有发送,其他(n-1)个站点中只有一个数据帧占用信道成功传输的概率,即在退避过程中检测到信道忙,同时又检测信道无冲突的概率。则有:
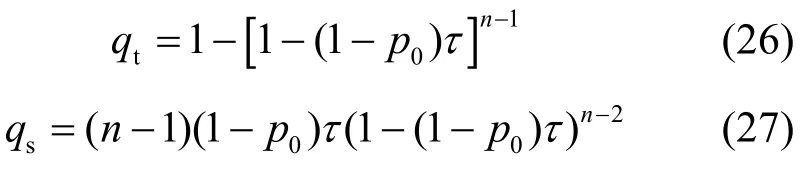
可以理解为在一个时隙σ之后,退避计时器以(1-qt)的概率减1,以概率qs保持原状态Ts时间,以概率(qt-qs)保持原状态Tc时间,所以退避计时器的递减过程是一个Markov过程,它的状态转移图3所示。
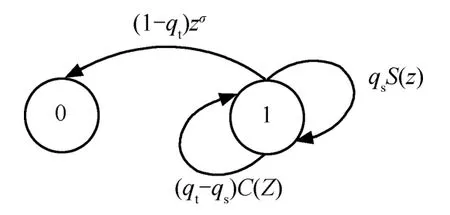
图3 退避递减过程的状态转移图
令 Hd(z)表示退避计时器递减过程所需时间的PGF,根据Mason公式,有:

3.4 MAC层服务时间
MAC层中数据帧的整个发送过程可以看作是一个z域的线性系统[19],令Hi(z)表示第i退避级数时退避过程所需时间的PGF,根据其服务系统的传递函数系统框图,可得:
令 μ-1为MAC层的平均服务时间,由式(30)和概率生成函数的性质,有:
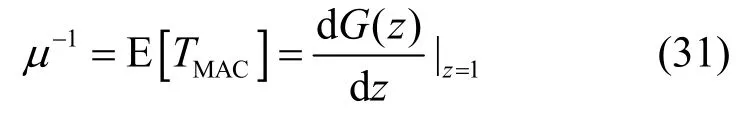
概率分布函数(PDF, probability distribution function)与PGF有以下关系:
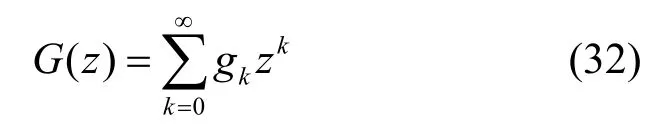
要计算MAC层服务时间的PDF,即求得gk,直接反z变换的复杂度很大,所以本文采用了Lattice-Poisson估计算法[20]
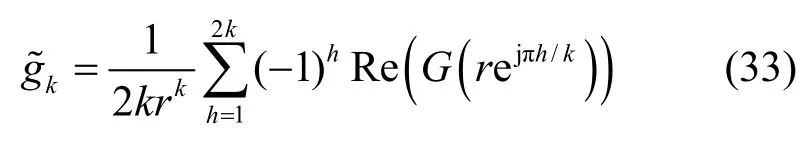
其中,Re()表示复数的实数部分。式(33)是通过将G(z)在半径为r(0<r<1)的圆上积分得到的。估计值与真实值gk之间的误差为
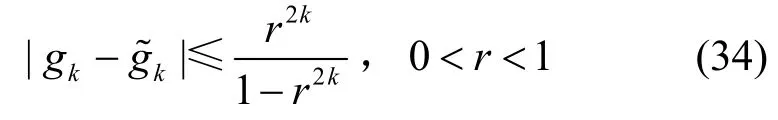
当r2k很小时,近似误差为r2k,令r=10-γ/2k,则精确度为10-γ,本文中设定γ=8。
图4和图5是站点数量n=10时MAC层服务时间的概率分布图,其中图4的μ-1=7.017 8ms,图5的μ-1=8.539 3ms。可以看到,RTS/CTS方式的接入时延要大于基本方式,这是因为,前者可以避免较大数据帧发送碰撞时造成的时间浪费,同时也带来了RTS和CTS控制帧的额外开销。由于M2M的数据帧长度较小,RTS/CTS方式反而没有了优势。
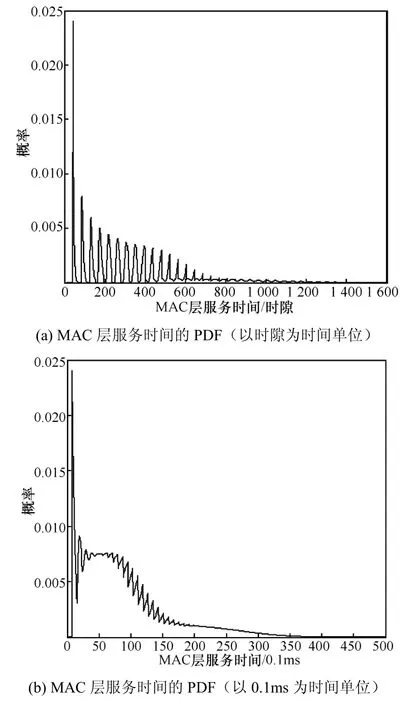
图4 MAC层服务时间的PDF(基本接入方式)
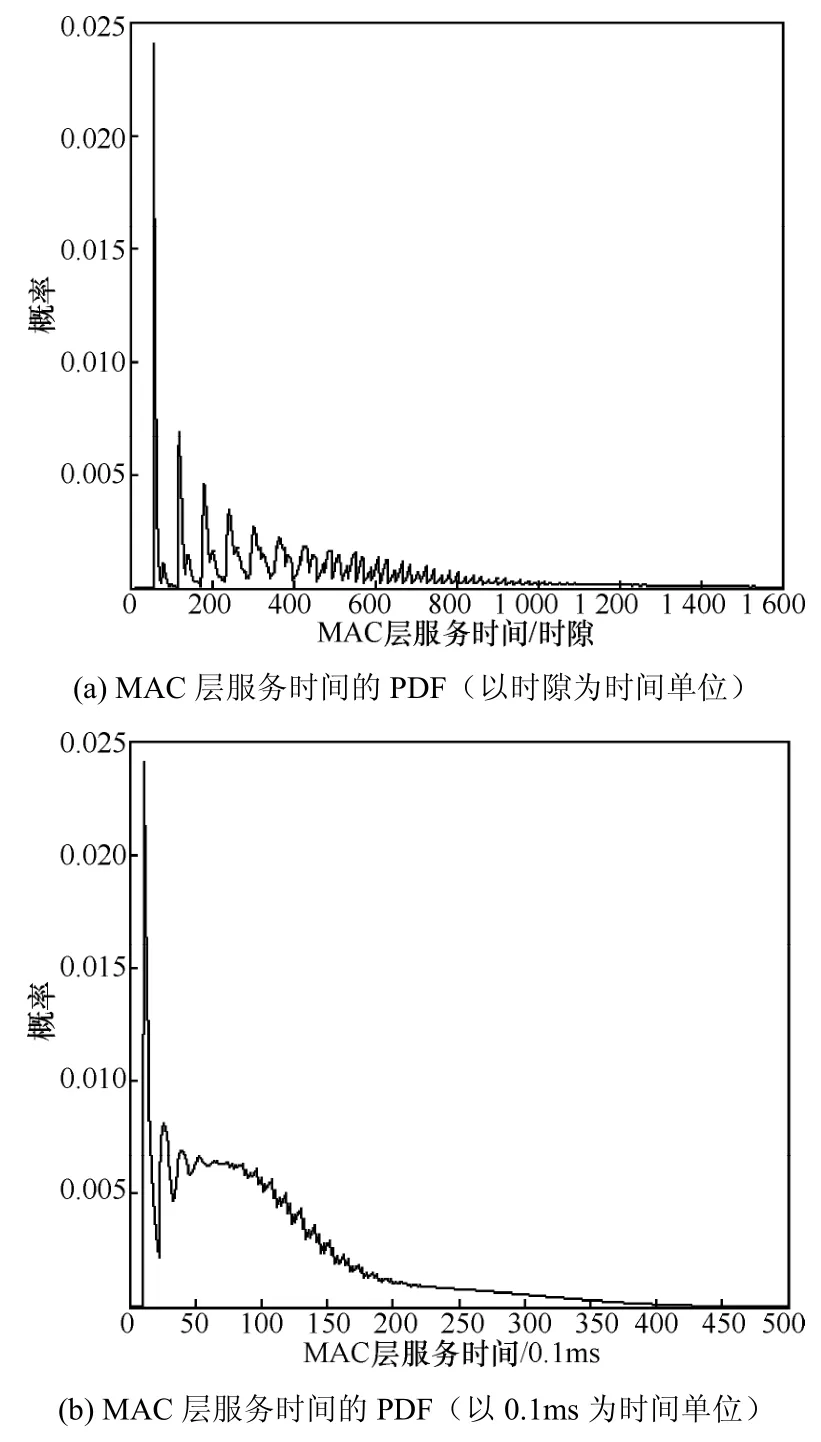
图5 MAC层服务时间的PDF(RTS/CTS方式)
4 IPP/G/1/K排队模型
将每个站点的缓存队列建模为一个IPP/G/1/K排队系统,其中,“IPP”指站点的业务到达过程都服从相同参数的IPP模型,服务时间分布“G”为已求得的一般函数MACT,“1”表示单服务器(即同一时间信道只能为一个数据帧服务),缓存队列长度为“K”。令J(t)(t≥0)表示在时隙t时IPP的状态,是一个二态不可约马尔可夫链;A(t)表示在[0,t)时间内IPP过程到达的数据帧数。则有:
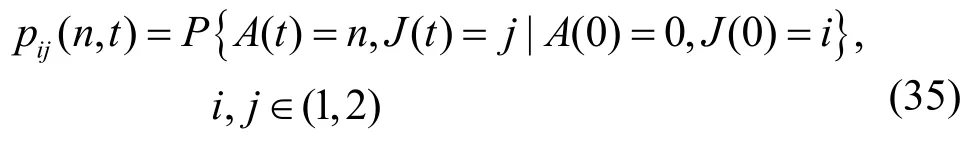
IPP过程的瞬时到达率为P(t)=eRt,那么可得
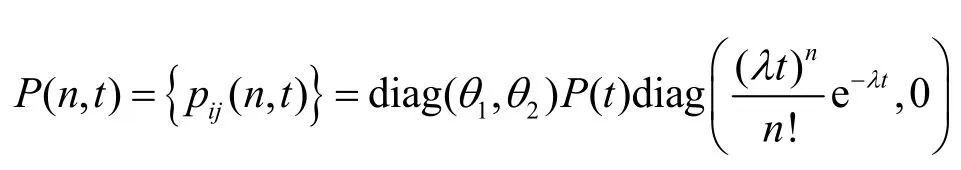
令X(t)表示时隙t缓存队列中的数据帧数,tn表示第n个数据帧离开瞬间的时刻。这样使就分别是tn之后排队系统的状态和IPP的状态,{Xn, Jn, n≥0}过程是一个二维的离散时间Markov链,可以称其为{X(t),J(t),t≥0}的嵌入马尔可夫链。有限的状态空间为{0,1,…,K-1}×{1,2},一步转移概率矩阵[21]

令πk,j是(Xn, Jn)的极限概率,稳态概率矢量π=(π0, π1,…,πK-1),πk=(πk,1,πk,2),0≤k≤K-1,通过求解线性系统πP=π,πe=1可以得到π,其中e=(1,1,…,1)T,全1的列向量,维数与π相同。
利用顾客离去时间嵌入马尔可夫链的方法研究IPP/G/1/K队列,并在这些特定时刻得到一个稳定的解,现在还必须研究任意时刻[22]。
设{X(t),J(t)}任意时刻的极限概率为xk,j,则有:
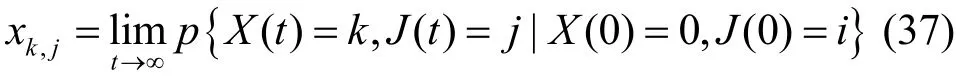
令x=(x0, x1,…,xK),xk=(xk,1,xk,2),系统忙的概率
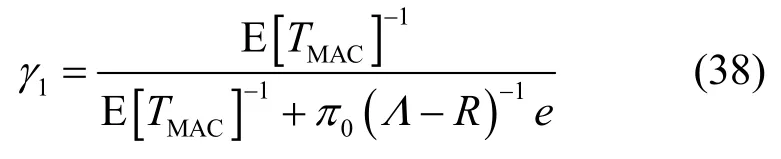
在嵌入时刻点与任意时刻稳态概率的关系为
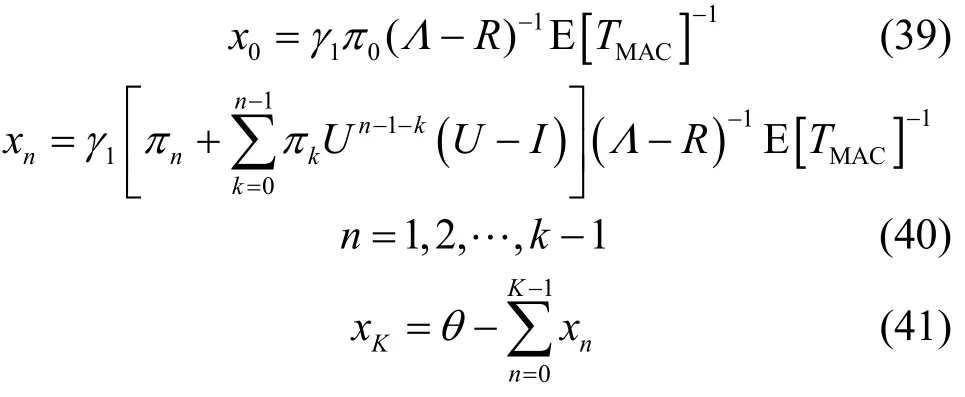
有效到达率λ*=θΛe ,可以得到各QoS参量,平均队长Q、阻塞率L、平均等待时间W、吞吐量S分别为
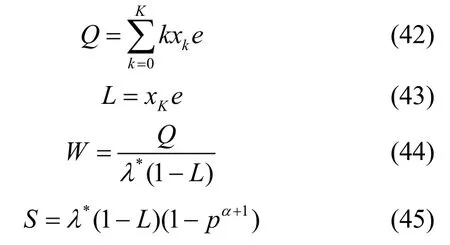
5 算法仿真结果分析
本文算法仿真以IEEE 802.11b DSSS作为物理层,采用基本接入方式,站点均处于非饱和状态,站点间的信道为非理想信道。根据IEEE 802.11标准,系统参数设置如表1所示。M2M业务到达是IPP过程,IPP参数通过NS2业务仿真确定,如表2所示,有效到达速率为1.2Mbit/s。在实验室NS2系统仿真平台上仿真了WLAN M2M业务系统,收集数据,完成业务参数拟合(实验室并行研究课题)。但是,仿真平台上对于M2M业务的模拟具有一定主观性。随着M2M的应用,可以根据实测数据进一步修正、优化业务到达模型、参数。
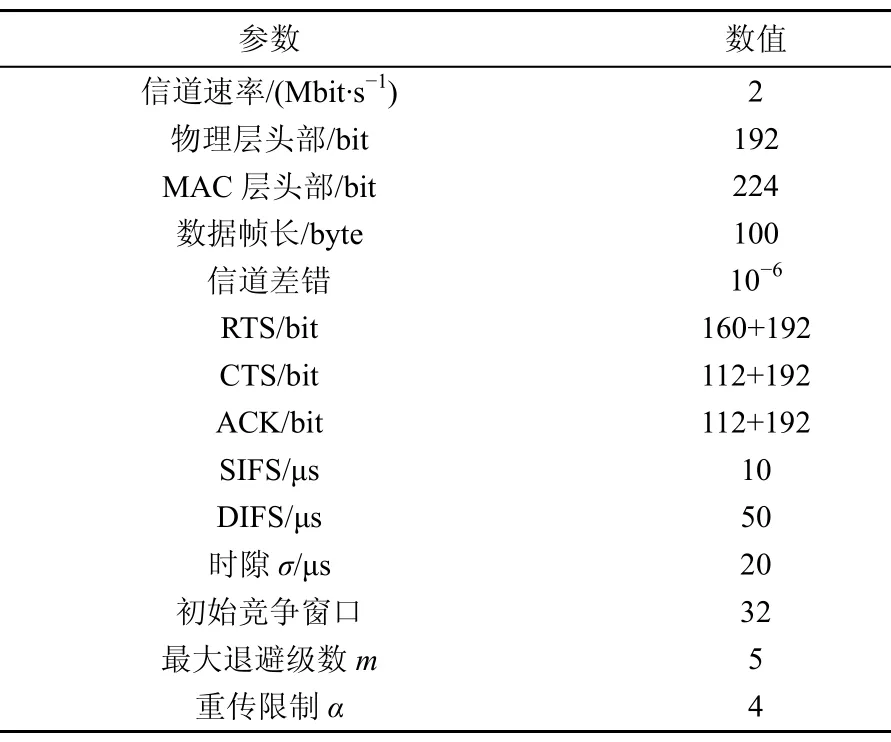
表1 802.11 DSSS PHY层和MAC层参数

表2 IPP模型参数
根据第3节和第4节的推导和本节的参数设置,可得到系统的时延、平均队长、阻塞率、吞吐量与站点数量的关系,如图6所示。从图6可以看出,大时间尺度退避机制引起系统平均队长和平均时延的增加,但是,图6(c)和图6(d)显示出,大时间尺度退避机制带来系统阻塞率的降低和吞吐量的上升,而且,随着站点数量的增加,吞吐量提高的效果越来越显著。M2M业务对时延的容忍性强,可以多次重试,而且,终端数量大(业界预测,M2M终端的数量将是H2H终端数量的30倍),因此,以时延的适当增加换来系统吞吐量的上升,阻塞率的下降,这样的改进算法对M2M通信是有效的。
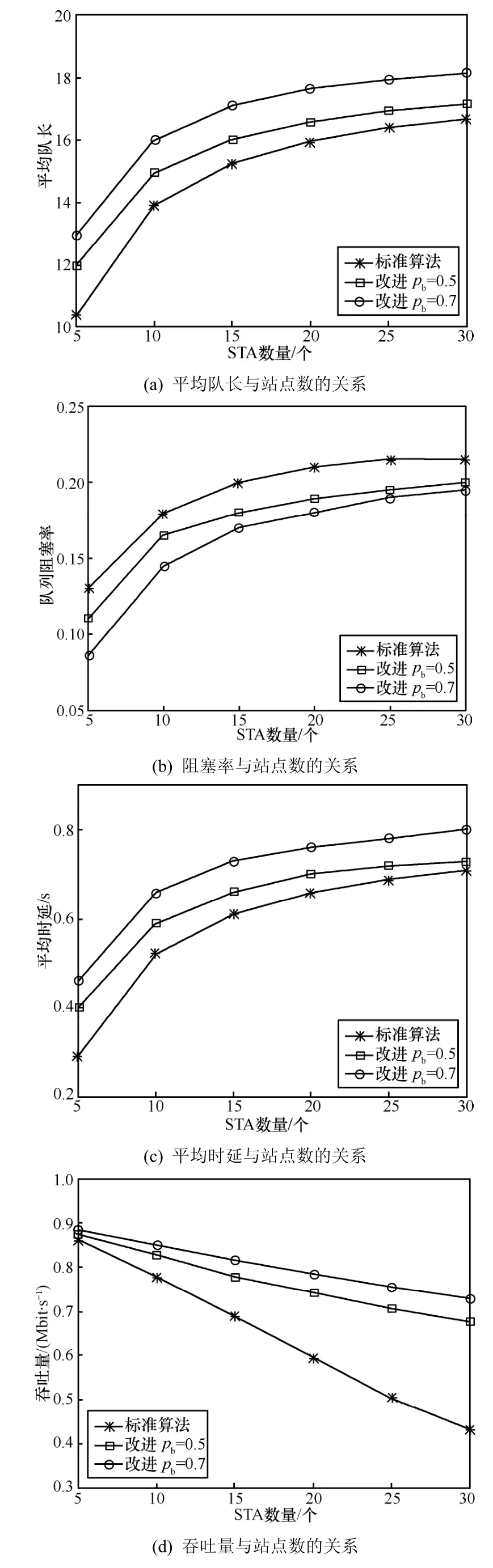
图6 各QoS参量与站点数的关系
6 结束语
本文针对M2M小数据业务的特点,首次以IPP过程模拟M2M小数据业务的到达分布,而且模型中的各参量可以根据业务特性动态调整。基于二维Markov模型研究了DCF的平均介质访问延迟的数学建模过程,提出大时间尺度退避算法,推导了MAC层服务时间的概率分布。结果表明,用二项式分布选择随机退避时间能够有效解决原有退避机制的高碰撞率问题,提高 WLAN的网络性能。本文将IEEE 802.11 WLAN的M2M站点建模为一个IPP/G/1/K离散时间排队系统,通过对这个排队模型的求解,得到M2M小数据业务在WLAN中的排队特性,如平均队长、排队时延、吞吐量等。算法仿真结果表明,本文提出的算法,提高了系统的吞吐量,尤其在站点数量大的条件下,算法显示出更明显的效果。
[1] International Telecommunication Union. Internet Reports 2005: the Internet of Things [R]. Geneva: ITU, 2005.
[2] TAN L, WANG N. Future Internet: the Internet of things[A]. IEEE ICACTE[C]. 2010.376-380.
[3] MARTINEZ C J J. How to selecting the optimum communications technology in intelligent hybrids nodes? A comparative view of IEEE 802.11b, bluetooth and UWB working together[A]. Future Information Technology (Future Tech)[C]. 2010.1-6.
[4] ANDERS O. M2M Traffic Characteristics[D]. Stockholm: Kungliga Tekniska Högskolan, 2009.
[5] BIANCHI G. Performance analysis of IEEE 802.11 distributed coordination function [J]. IEEE JSAC, 2000, 18(3): 535-547.
[6] ZIOUVA E, ANTONAKOPOULOS T. CSMA/CA performance under high traffic conditions: throughput and delay analysis[J]. Computer Communications, 2002, 25(3): 313-321.
[7] WU H, PENG Y, LONG K. Performance of reliable transport protocol over IEEE 802.11 wireless LAN: analysis and enhancement[A]. Proc IEEE INFOCOM[C]. 2002. 599-607.
[8] HADZI V Z, SPASENOVSKI B. Saturation throughput–delay analysis of IEEE 802.11 DCF in fading channel[A]. Proc IEEE ICC[C].2003. 121-126.
[9] LIU R P, SUTTON G J, COLLINGS I B. A new queueing model for QoS analysis of IEEE 802.11 DCF with finite buffer and load[J]. IEEE Transactions on Wireless Communications, 2010, 9(8): 2664-2675.
[10] CHOI J, YOO J, KIM C K. A novel performance analysis model for an IEEE 802.11 wireless LAN [J]. IEEE Communication Letters, 2006,10(5): 335-337.
[11] 薛俊晗, 张晓敏, 陈高明. 基于排队模型的无线局域网性能分析[J].计算机工程, 2010, 36(10): 133-139.XUE J H, ZHANG X M, CHEN G M. Performance analysis of wireless LAN based on queuing model[J]. Computer Engineering, 2010,36(10): 133-139.
[12] LEE W, WANG C G, SOHRABY K. On use of traditional M/G/1 model for IEEE 802.11 DCF in unsaturated traffic conditions[A].IEEE WCNC[C]. 2006.1933-1937.
[13] VARDAKAS J S, SIDIROPOULOS M K, LOGOTHETIS M D.Performance behaviour of IEEE 802.11 distributed coordination function[J]. IET Circuits Devices Syst, 2008, 2(1): 50-59.
[14] TICKOO O, SIKDAR B. Queueing analysis and delay mitigation in IEEE 802.11[A]. Proc IEEE INFOCOM[C]. HongKong, China, 2004.1404-1413.
[15] OZDEMIR M, MCDONALD A B. A queuing theoretic model for IEEE 802.11 DCF using RTS/CTS[A]. Proc IEEE Workshop LANMAN[C]. 2004. 33-38.
[16] ZHAI H, KWON Y, FANG Y. Performance analysis of IEEE 802.11 MAC protocols in wireless LANs[J]. Wiley J Wirel Commun Mob Comput, 2004, 4(8): 917-931.
[17] 3GPP TS 22.368 V1.0.0 (2009-08), Service Requirements for Machine-Type Communications[R].
[18] PARK C G, HAN D H, AHN S J. Performance analysis of MAC layer protocols in the IEEE 802.11 wireless LAN[J]. Telecommunication Systems, 2006, 33(1-3): 233-253.
[19] ZHENG Y, LU K, WU D. Performance analysis of IEEE 802.11 DCF in imperfect channels[J]. IEEE Trans Veh Technol, 2006, 55(5): 1648-1656.
[20] ABBATE J, WHITT W. Numerical inversion of probability generating functions[J]. Oper Res Lett, 1992, 12(4): 245-251.
[21] GROSS D, HARRIS C M. Fundamentals of Queueing Theory (Third Edition)[M]. New York: John Wiley & Sons, Inc, 1998.
[22] BAIOCCHI A, BLEFARI M N. Steady-state analysis of the MMPP/G/l/K queue [J]. IEEE Transactions on Communications, 1993,41(4): 531-534.

