面向异构网络环境的蠕虫传播模型Enhanced-AAWP
刘波,王怀民,肖枫涛,陈新
(国防科技大学 计算机学院,长沙 湖南 410073)
1 引言
随着以 Internet为代表的网络及其承载的网络应用日益表现出成长性、自治性和多样性的特点[1],在系统、网络、应用以及管理等各个层面上暴露出来的大量漏洞或者脆弱性,导致以蠕虫为代表的恶意代码对网络基础设施以及网络应用的破坏程度明显增加。尤其是当蠕虫在继续保持了自我复制和主动传播特性的同时,更多地将 Rootkit技术应用于自身的隐蔽,或者被攻击者赋予了相应的通信能力,形成各种类型的僵尸网络之后,恶意代码已经愈发成为影响网络安全的最严重威胁之一。
从攻击者的角度而言,在使用蠕虫类恶意代码实施网络攻击时,如何能够在尽可能短的时间内发现并且感染网络中尽可能多的潜在攻击目标通常是其追求的首要目标。即使攻击者的最终意图是形成具有某种控制结构的恶意网络,利用蠕虫类恶意代码的渗透传播也是攻击者感染网络中大量脆弱性主机的主要途径。因此,作为蠕虫类恶意代码研究的重要内容之一,能否合理地建立蠕虫传播模型,使用数学建模的方法相对准确地反映蠕虫在网络中进行渗透传播时其数量规模随传播时间而发生的动态变化,深入分析包括扫描策略在内的多种因素可能对蠕虫的渗透传播过程产生的潜在影响,为更有针对性地开展蠕虫防护、检测以及抑制技术的研究提供必要的理论依据,对于有效地遏制蠕虫类恶意代码所形成的严重威胁具有极为重要的意义。
2 蠕虫传播模型的研究进展与分析
虽然在 Internet中爆发过的大量蠕虫曾经使用过随机扫描、顺序扫描、本地优先扫描、内部目标列表扫描、外部目标列表扫描等多种不同的扫描策略[2~4],但是从本质上而言,这些采用了不同扫描策略的蠕虫在自我复制、主动传播等特性上都与生物界中的病毒极为相似。同时,病理学领域中对传染性疾病在人群中的感染过程进行建模的大量研究也已经表明,确定性的分析方法可以很好地用于对大规模系统的动态特性变化进行建模[5]。因此,在研究生物病毒的传染过程时所形成的部分数学模型及其分析方法就被很自然地应用于蠕虫的渗透传播机制研究,形成了若干具有代表性的蠕虫传播模型。
2.1 基于简单传染病模型的蠕虫传播模型研究
简单传染病模型(SEM, simple epidemic model)[6]首先假设网络中每台可能被感染的脆弱性主机在蠕虫的传播过程中可能分别处于易被感染(susceptible)和已被感染(infected)2种不同的状态:在蠕虫开始传播之前,所有的脆弱性主机均处于Susceptible状态;随着蠕虫在网络中的传播,被感染的脆弱性主机将从 Susceptible状态转变为Infected状态,并且在随后的蠕虫传播过程中始终保持Infected状态。亦即,网络中的脆弱性主机将只可能出现由Susceptible状态到Infected状态的转换,因此,SEM模型也被称为SI模型。其次,SEM模型还假设网络中每台处于Infected状态的脆弱性主机,将以相同的概率尝试感染网络中其他仍然处于Susceptible状态的脆弱性主机。这实际上意味着蠕虫将在同构的网络环境中进行传播。
如果以N表示在蠕虫开始传播之前网络中所有处于Susceptible状态的脆弱性主机数量,I(t)表示在某个时刻t,网络中已经被蠕虫感染的处于Infected状态的脆弱性主机数量,那么SEM模型可以表示为如式(1)所示的微分方程[6],其中β被称为双向的感染率,代表了在某个时刻t,网络中已经被感染的脆弱性主机对易被感染的脆弱性主机的感染强度或者感染能力。
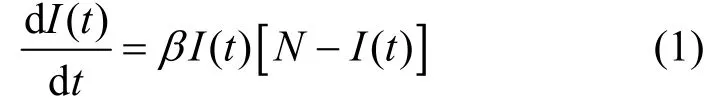
基于 SEM 模型类似的假设条件以及时间连续的分析方法,通过研究处于Infected状态的脆弱性主机可能由于所感染的蠕虫实例被清除而发生的状态转换,分别形成了 SIS模型[7]和 Kermack-Mckendrik模型[8](即KM模型,也称SIR模型);而双因素模型[9](two-factor worm model)又在KM模型的基础上进一步分析了处于Susceptible状态的脆弱性主机可能由于修补了相应的漏洞而发生状态转换,以及蠕虫自身的大量繁殖可能引起网络拥塞等因素对于蠕虫传播过程的影响。
2.2 AAWP模型(analytical active worm propagation model)
Z. Chen等在开展蠕虫传播模型的研究时提出,如果以经典的传染病模型为基础,使用时间连续的分析方法来研究蠕虫的渗透传播过程,那么将很难合理地反映部分重要的时间因素可能对蠕虫的传播过程所产生的影响:首先,每个蠕虫的实例感染下一个处于Susceptible状态的脆弱性主机是需要时间来完成的。在某个处于Susceptible状态的脆弱性主机被完全感染之前,这个脆弱性主机不会转变到Infected状态,亦即没有传染性;而使用时间连续的微分方程来估算网络中被感染的脆弱性主机数量的动态增长,就意味着在每个具体时刻t,都可能有若干“被部分感染”的脆弱性主机将参与对其他仍然处于Susceptible状态的脆弱性主机的感染,这就与实际的蠕虫传播过程存在着一定的差异。其次,不同种类的蠕虫具有不同的感染能力,这个感染能力不仅取决于蠕虫实例的平均扫描速率,或者双向的感染强度,还取决于蠕虫的各个实例在感染具体目标时需要花费的时间。因此,在分析蠕虫的渗透传播过程时还必须综合考虑感染时间这个因素的可能影响[10]。
基于这种认识,Z. Chen等使用时间离散的确定性分析方法提出了蠕虫传播模型AAWP,用于分析采用随机扫描策略的蠕虫在 IPv4网络地址空间中的渗透传播。在AAWP模型中,蠕虫的实例完成对下一个潜在目标的扫描和感染所需要的时间被称为一个时间单元。同时,为了降低分析过程的复杂性,AAWP模型假设当蠕虫的某个实例发出的某次扫描选择了网络中的某个 IP地址之后,无论该IP地址是否被使用、(如果IP地址被使用,对应的)目标主机是否存在脆弱性、(存在脆弱性的)目标主机是否已经被蠕虫的其他实例所感染,这个蠕虫实例都将花费一个完整的时间单元来实施相应的攻击行为。
如果以mi和ni分别表示在第i个时间单元(0i≥)结束时,网络中(包含已经处于Infected状态和仍然处于Susceptible状态的)脆弱性主机的数量和已经处于Infected状态的脆弱性主机数量,η表示蠕虫实例的平均扫描速率。那么在第 1i+个时间单元结束时,网络中处于Infected状态的被感染主机数量1in+可由式(2)计算获得[10]:
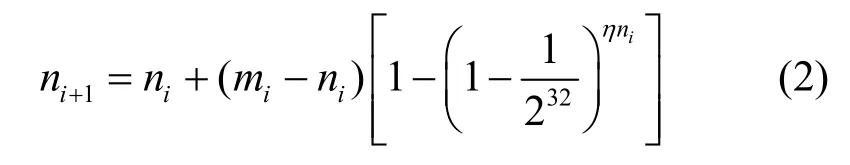
2.3 网络环境的异构性
无论是使用时间连续的分析方法还是时间离散的分析方法来研究蠕虫的渗透传播过程,概括而言,都是以尽量合理地抽取可能影响到蠕虫传播速度的多种潜在因素为出发点,力争更加准确地估算出在蠕虫开始传播后的某个时刻t,网络中被蠕虫所感染的脆弱性主机数量。
但是在上述代表性的蠕虫传播模型研究中普遍忽略了一个关键环节,这就是在病理学研究领域,传染病模型的基本假设是将大量可能被感染的潜在目标视为同构群体。这个假设很好地与传染性疾病在易感人群中的传播过程相吻合。而当把传染病模型应用于研究蠕虫类恶意代码在网络中的渗透传播时,如果仍然基于类似的假设,将典型如Internet的目标网络视为同构网络,即网络中的脆弱性主机是均匀地分布在网络地址空间中,而且处于Susceptible状态的脆弱性主机将有相同的概率被网络中所有其他处于Infected状态的脆弱性主机所感染,那么这种假设就与目标网络的实际情况可能存在着一定程度的出入。类似的,虽然Z. Chen等在对 AAWP模型做出相应的扩展后又进一步地提出了LAAWP模型[10],用以分析采用了本地优先扫描策略的非均匀扫描蠕虫在网络中的渗透传播过程,但是无论AAWP模型还是LAAWP模型,都还是以同构网络作为其研究的基本假设[11],并没有考虑到网络环境的异构性可能对蠕虫的渗透传播过程产生潜在影响。
实际上,以 Internet为例,各种蠕虫在渗透传播时所处的是一个高度异构的网络环境,这与上述代表性的蠕虫传播模型所假设的扁平化同构网络环境具有相当大的差异。
1) 首先,Internet是由若干以不同方式连接的自治系统或者管理域所组成。蠕虫在各个管理域的内部以及管理域之间的渗透传播可能分别表现出不同的动态特性变化。例如,Serazzi等结合对Slammer蠕虫的传播数据进行分析后指出,Internet中自治系统之间的网络互联是影响Slammer蠕虫传播过程的瓶颈之所在[12]。
2) 其次,网络中存在相应的漏洞,可能被蠕虫所感染的脆弱性主机在整个网络地址空间中的分布是不均匀的。从本质上而言,这种脆弱性主机的不均匀分布也是由于 Internet被划分为不同管理域的必然结果。以Z. Chen等对可能存在漏洞的网络服务在各个网络区域中的采样数据为例,无论是以DNS顶级管理域,还是以国家、自治系统、A类/8网络或者B类/16网络作为不同网络区域的划分标准,所采样的网络服务在各个网络区域之间均表现出明显的不均匀分布[13]。Rajab等则通过分析分布式入侵检测系统 Dshield[14]的日志数据,进一步地证实了可能已经被Code Red、Nimda、MS Blaster等蠕虫所感染的脆弱性主机在 Internet中的分布是不均匀的[11]。
3) 再次,越来越多的网络用户使用私有IP地址,通过NAT技术接入Internet。Casado等在对监测到的Code Red II蠕虫的流量数据进行分析后认为,网络中有60%左右被Code Red II蠕虫所感染的计算机使用了私有IP地址或者动态IP地址,经由NAT之后接入Internet[15]。类似的,Rajab等也通过网络监测的方法对 NAT技术的使用情况进行了估算,结果显示大约有19%的具有感染性的计算机通过使用NAT技术接入Internet[16]。虽然这2种研究方法在具体数字上存在着一定程度的差异,但是其研究结论共同反映了NAT技术在Internet中已经被广泛运用的事实。
因此,针对上述蠕虫传播模型研究在“同构网络”这个前提假设上可能存在的缺陷,下文将首先抽象出分层的异构网络模型用于反映 Internet的异构特性,并以之作为开展蠕虫传播模型研究的基本前提。同时,鉴于AAWP/LAAWP模型所使用的时间离散的确定性分析方法可以相对合理地反映出感染时间在蠕虫的渗透传播过程中产生的潜在影响,下文将继续基于时间离散的确定性分析方法,全面、深入地分析蠕虫在异构网络环境中的渗透传播过程。这个面向异构网络环境的、以AAWP/LAAWP模型为基础进行优化的蠕虫传播模型将被称为Enhanced-AAWP模型。
3 面向异构网络环境的蠕虫传播模型研究
3.1 分层的异构网络模型抽象
Enhanced-AAWP模型使用分层的异构网络模型来抽象蠕虫在渗透传播过程中所处的以 Internet为代表的异构网络环境,具体如图1所示。
1) 上层的宏观网络中,蠕虫传播的异构网络环境可以被视为由多个相互连接的自治系统或者不同的管理域所组成。
2) 下层的实体网络中,并非所有的IPv4地址均全局路由可达。每个自治系统或者管理域内部的联网计算机既有可能被分配了全局路由可达的 IP地址,也有可能被分配了私有或者动态的IP地址,通过使用 NAT技术接入上层由自治系统或者管理域相互连接而成的全局网络。
3) 处于 Susceptible状态、可能被蠕虫在传播过程中所感染的脆弱性主机在这些自治系统或者管理域之间的分布可能是不均匀的。同时,为了模型的简化,可以假设在各个自治系统中,Susceptible状态的脆弱性主机在全局路由可达的网络区域内是均匀分布的;类似的,在每个 NAT子网中,也可以假设Susceptible状态的脆弱性主机是均匀分布的。
3.2 Enhanced-AAWP模型的分析方法
由于脆弱性主机在各个自治系统之间的分布是不均匀的,因此在基于分层的异构网络模型、使用时间离散的确定性分析方法具体分析蠕虫的渗透传播过程时,其作用域不再是单独每台可能处于Susceptible状态的脆弱性主机,而是会被应用到网络中可能包含有若干台脆弱性主机的各个不同的网络区域,通过相应地计算蠕虫的实例所发出的扫描动作可能进入到各个网络区域的数量,对蠕虫在不同网络区域中的传播过程分别进行建模,再以之为基础综合形成面向异构网络环境的蠕虫传播模型。
为了将 Enhanced-AAWP模型的研究重点集中在对蠕虫渗透传播机制的内在本质特性进行深入分析,因此下文暂时忽略了蠕虫在渗透传播的过程中可能会受到网络安全防护措施或者人工干预等外在因素的潜在影响。在这个前提下,以 AAWP模型为基础,Enhanced-AAWP模型也可以使用下面的引理作为基本的分析依据。
引理 对于某个地址空间规模为ω的网络区域而言,如果 1)初始状态下该网络区域中处于Susceptible状态的脆弱性主机数量为N,2)在第i个时间单元,该网络区域中处于Infected状态的脆弱性主机数量为iI,3)在第 1i+ 个时间单元内命中该网络区域的蠕虫扫描次数为S,那么可由式(3)计算出在第 1i+个时间单元内该网络区域中新被蠕虫感染的脆弱性主机数量:
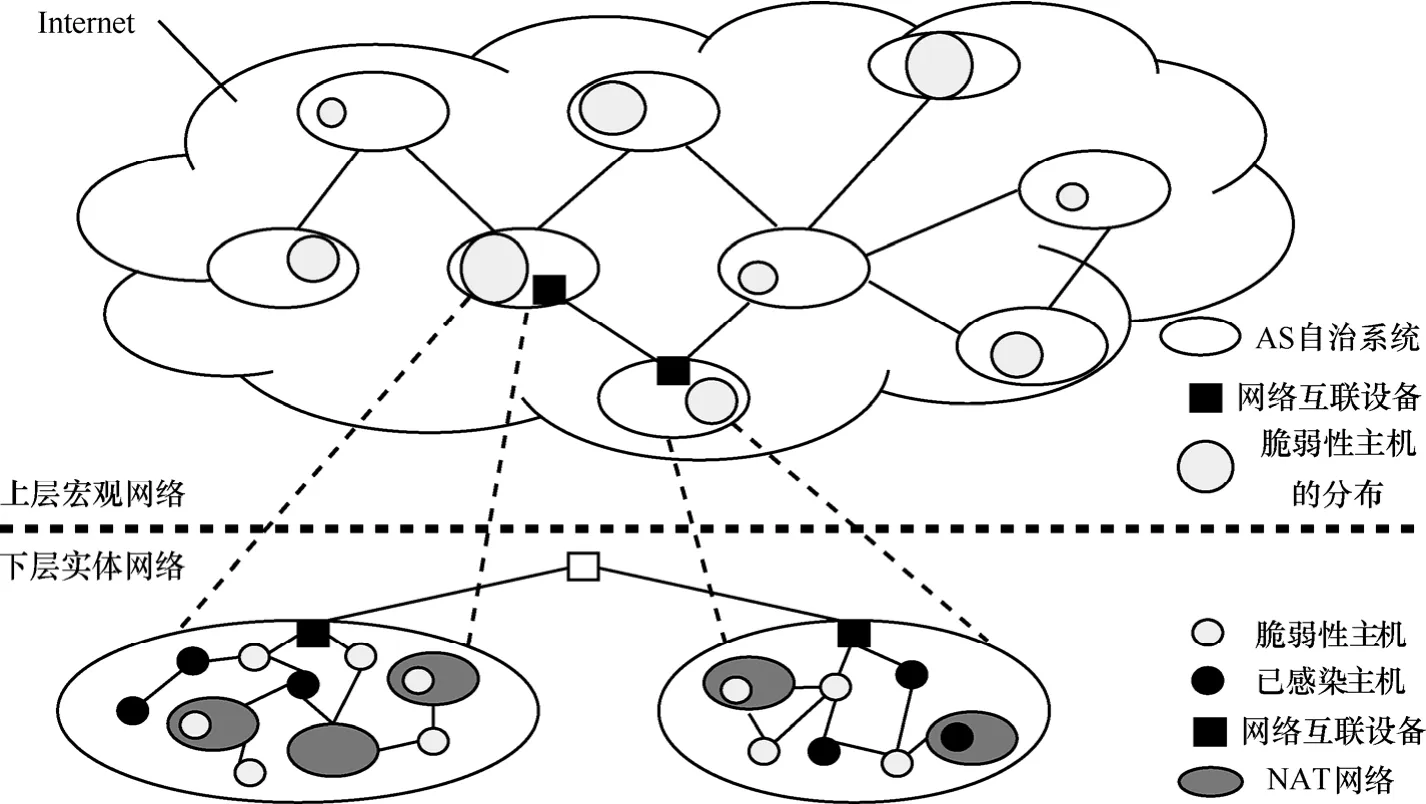
图1 分层的异构网络模型
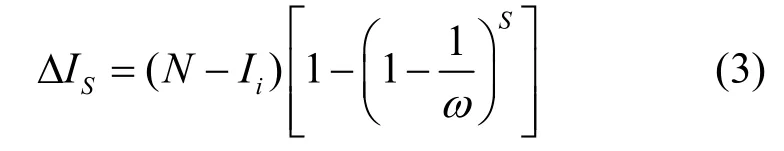
与AAWP模型的分析方法[10]相类似,引理的证明可以通过归纳法来完成:
1) 当S=1时,由于此时网络中存在N-Ii台处于Susceptible状态的脆弱性主机,因此命中该网络区域的此次扫描有的可能使得某台处于Susceptible状态的脆弱性主机转换到Infected状态,即
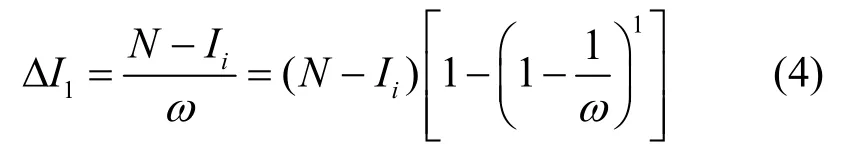
2) 假设Sn=当时定理成立,即
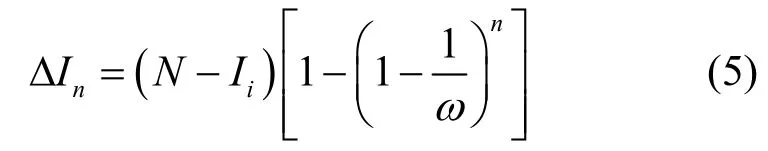
那么当1Sn=+时,在前n次扫描完成之后,第1n+次扫描命中该网络区域中某台Susceptible状态的脆弱性主机的概率为,而第n+1次扫描未命中该网络区域中任何Susceptible状态的脆弱性主机的概率为1-。因此,当有1n+次扫描命中该网络区域之后,新增的Infected状态的脆弱性主机数量1nI+Δ可以由式(6)计算获得:
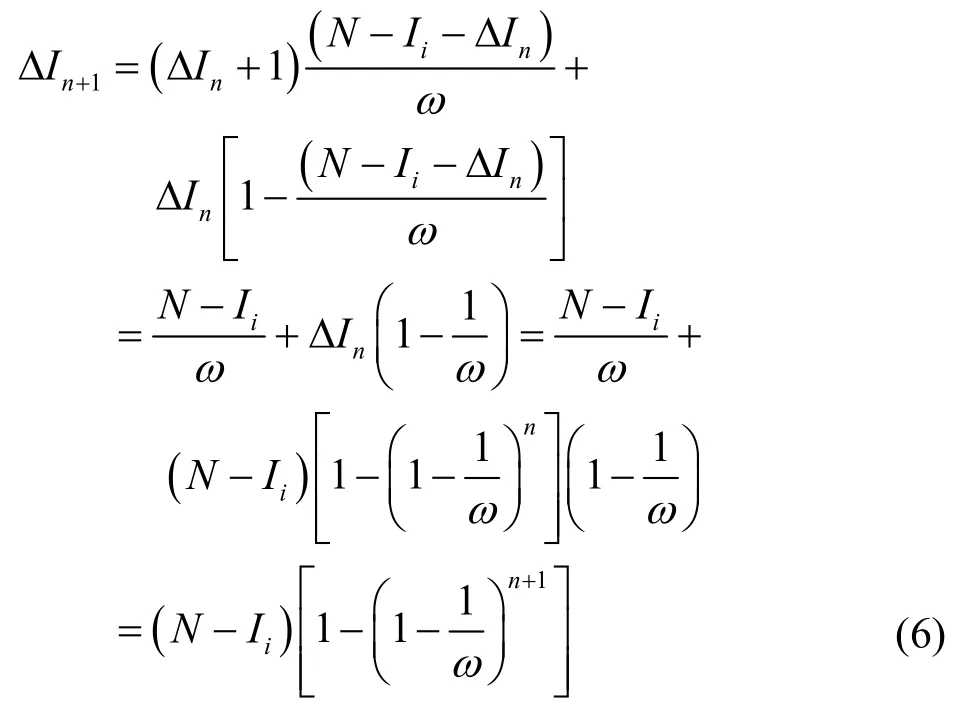
综上,引理成立,证毕。
这就意味着,AAWP模型对蠕虫在IPv4地址空间中的传播过程进行分析的方法,在不同规模的网络区域中仍然具有可适性,可以之作为出发点开展面向异构网络环境的蠕虫传播模型研究。
3.3 Enhanced-AAWP模型与本地优先扫描策略分析
为了简化Enhanced-AAWP模型的分析过程而又不失一般性,可以进一步地对异构网络环境以及蠕虫在这个异构网络环境中的渗透传播过程做出以下假设。
1) 网络中由于存在漏洞而可能被感染的脆弱性主机在蠕虫的整个传播过程中将分别处于2种状态:易被感染的Susceptible状态和已被感染的Infected状态;当某个Susceptible状态的脆弱性主机被蠕虫的某个实例所感染后,将在后续的蠕虫传播过程中始终处于Infected状态。
2) 蠕虫将在由K个相互连接的不同自治系统所组成的网络环境中进行渗透传播。
3) 在每个自治系统i中,全局路由可达的网络分别是子网前缀可能不同的/ni网络,对应的IP地址集合为Vi,网络地址空间大小为初始处于Susceptible状态的脆弱性主机数量为Ni。
4) 在每个自治系统i中,分别有iM个NAT子网接入到网络中,并且:
①这Mi个NAT子网分别是可能具有不同子网前缀的/n'i,l网络,1≤l≤Mi;
②在每个/n'i,l的NAT子网内,IP地址集合为Vi,′l,网络地址空间大小为,初始处于Susceptible状态的脆弱性主机数量为Ni′,l;那么,每个自治系统i中所有NAT子网对应的IP地址集 合Vi′=UVi′,l,网 络 地 址 空 间 大 小1≤l≤Mi;
③在每个/,'iln的NAT子网内,所有的IP地址均为全局路由不可达状态,即所有处于NAT子网内的Susceptible状态的脆弱性主机只可能被处于相同NAT子网内的Infected状态的脆弱性主机上的蠕虫实例所感染。
5) 如图2所示,蠕虫实例具有初步的智能性,将使用经过优化的单级本地优先扫描策略在上述异构的网络环境中选择下一轮攻击的潜在目标:
① 以Pl的可能性完成本地网络扫描,在与被这个蠕虫实例所感染的Infected状态脆弱性主机相同的/n′i,l网络或者/in网络中随机地选择下一个潜在的攻击目标;
② 以Pr=1-Pl的可能性在包含上述/n′i,l网络或者/ni网络的整个扫描空间(例如IPv4地址空间)中随机地选择下一个潜在的攻击目标;
③ 蠕虫实例所发出的上述扫描动作,分别被称为Pl扫描和Pr扫描。
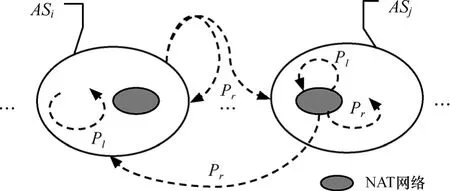
图2 蠕虫在异构网络环境中的本地优先扫描
6) 无论Infected状态的脆弱性主机是位于全局路由可达的网络内还是某个NAT子网内,感染这个脆弱性主机的蠕虫实例都需要花费一个完整的时间单元以完成对下一个潜在攻击目标的扫描和感染;当某个时间单元结束时,在这个时间单元内被感染的所有原处于Susceptible状态的脆弱性主机都将转换为Infected状态。
根据Enhanced-AAWP模型的研究假设,目标网络的地址空间大小为,那么当蠕虫在渗透传播过程中需要覆盖整个目标网络时,需要扫描的地址空间大小Ω应该大于232-niK+′。同时,上述假设也给出了一个经过优化的、具有某种程度适应性的本地优先扫描策略,即每个蠕虫实例可以根据传播时所处的具体网络环境来确定接下来实施lP扫描和rP扫描时分别需要考虑的扫描范围。
Enhanced-AAWP模型在分析蠕虫的渗透传播过程时所使用的符号及其含义如表1所示。
根据Enhanced-AAWP模型的假设,对于某个自治系统i中第l个NAT子网而言,由于NAT子网内的地址均为全局路由不可达,因此在第t+1个时间单内,只有这个NAT子网内个处于Infected状态的脆弱性主机发出的ηPl次Pl扫描,以及次Pr扫描才有可能继续命中这个子网。那么根据引理,在第t+1个时间单元结束时,自治系统i中第l个NAT子网内处于Infected状态的脆弱性主机数量如式(7)所示:
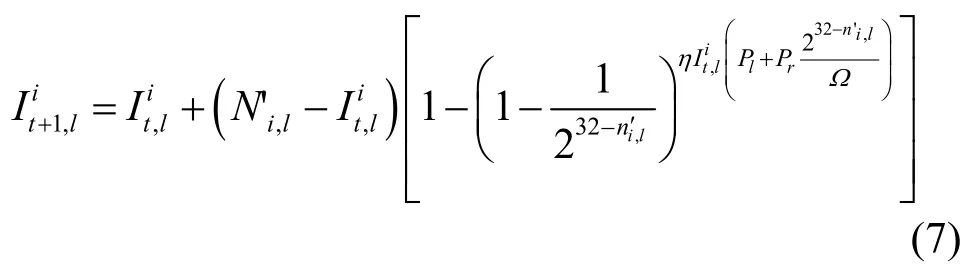

表1 Enhanced-AAWP模型使用的符号及其含义
因此,在第1t+个时间单元结束时,可由式(8)计算出自治系统i中所有Mi个NAT子网内处于Infected状态的脆弱性主机总数:
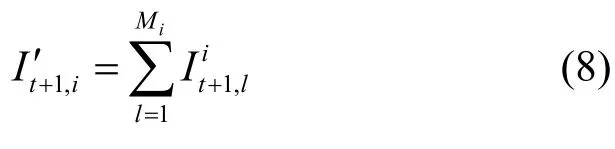
另一方面,对于自治系统i中全局路由可达的网络区域,根据Enhanced-AAWP模型的假设,在第t+1个时间单元内可能命中这个网络区域的扫描有两类:
1) 自治系统i中全局路由可达网络区域内的It,i个Infected状态的脆弱性主机所发出的Pl扫描,将继续命中这个自治系统中全局路由可达的网络区域;
2) 除了自治系统i中全局路由可达的网络区域内It,i个Infected状态的脆弱性主机发出的Pl扫描外,整个异构的网络环境中所有It个Infected状态的脆弱性主机发出的Pr扫描,也将以的概率命中自治系统i中全局路由可达的网络区域。
因此,在第t+1个时间单元内命中自治系统i中全局路由可达网络区域的扫描次数 S可由式(9)计算获得:
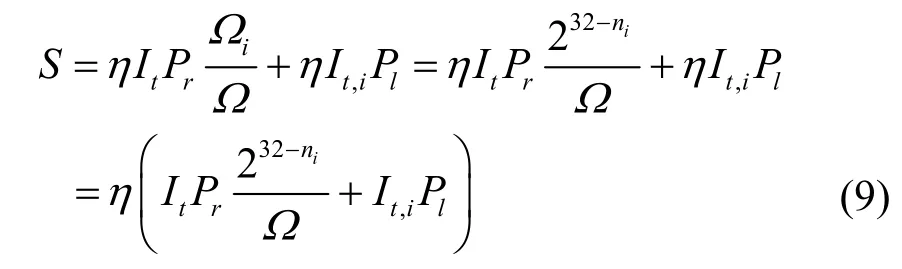
于是,在第t+1个时间单元结束时,可由式(10)计算出自治系统i中全局路由可达的网络区域内处于Infected状态的脆弱性主机数量:
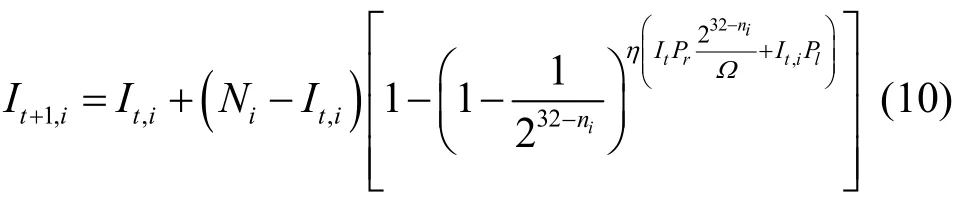
综上,在第t+1个时间单元结束时,式(11)给出了整个异构的网络环境中已经被蠕虫所感染的处于Infected状态的脆弱性主机数量:
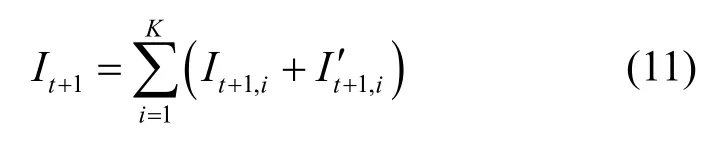
以 Enhanced-AAWP模型对上述这个经过优化的单级本地优先扫描策略进行分析的方法为基础,可以方便地在扩展后对更复杂的多级本地优先扫描策略,例如Code Red II蠕虫所使用的两级本地优先扫描策略进行相应的分析。
3.4 均匀的随机扫描策略分析
如果在基于Enhanced-AAWP模型分析上述优化的单级本地优先扫描策略时取 Pr= 1 (相应地有 Pl= 0 ,即每个蠕虫实例不会基于本地网络优先的原则发出 Pl扫描),那么这个单级本地优先扫描策略将完全等价于均匀的随机扫描策略。亦即,如果基于Enhanced-AAWP模型来分析蠕虫在异构网络环境下的渗透传播过程,那么可以相应地将随机扫描策略视为本地优先扫描策略的一个特例。
首先,对于某个自治系统i中第l个NAT子网而言,在第 t +1个时间单内,这个NAT子网内个处于Infected状态的脆弱性主机发出的所有η次Pr扫描,将以的概率继续命中这个子网。那么在第 t +1个时间单元,自治系统i中第l个 NAT子网内处于Infected状态的脆弱性主机数量可由式(12)计算获得:
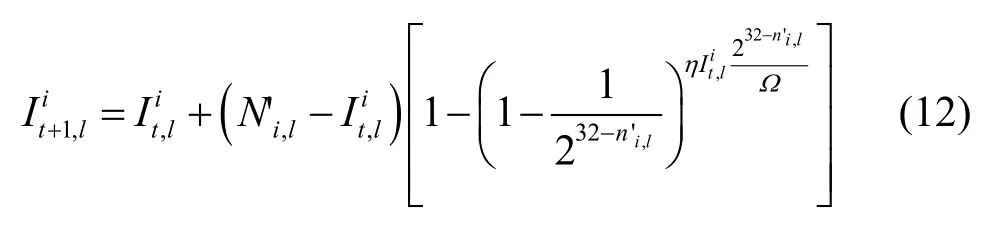
其次,对于自治系统i中全局路由可达的网络区域,由于在第t+1个时间单元内可能命中这个网络区域的扫描次数为,因此在第t+1个时间单元结束时,自治系统i中全局路由可达的网络区域内处于Infected状态的脆弱性主机数量将由式(13)计算获得:
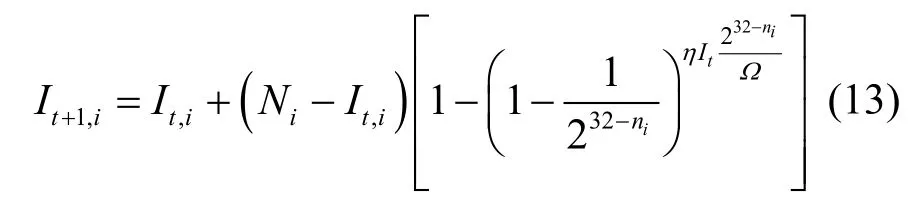
综上,可由式(14)计算出在第t+1个时间单元结束时,整个异构的网络环境中已经被该随机扫描蠕虫所感染的处于 Infected状态的脆弱性主机数量:
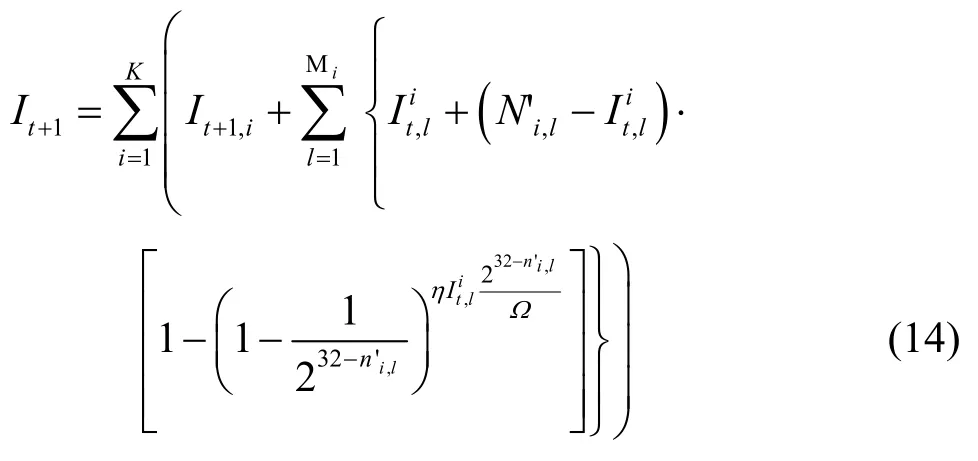
4 Enhanced-AAWP模型的模拟与分析
S. R. White在研究计算机病毒的传染过程时曾经指出,计算机病毒的实际传播速度要滞后于传染病模型的预期[17]。那么当蠕虫在Internet等异构的网络环境中进行渗透传播时,是否也存在着类似的现象呢?以Code Red蠕虫为例,图3(a)给出了D.Moore等根据CAIDA的监测数据所绘制的Internet中被蠕虫所感染的脆弱性主机数量动态增长的传播曲线[18];而以 IPv4地址空间中初始处于Susceptible状态的脆弱性主机数量 N = 3 59000、初始处于Infected状态的脆弱性主机数量 I0= 1、蠕虫实例的平均扫描速率η=6作为模拟参数,使用Matlab分别对SEM模型和AAWP模型进行模拟后得到的传播曲线如图3(b)所示(模拟参数N、η的选择参考了C. C. Zou等对Code Red蠕虫的分析数据[19];而在模拟 AAWP模型时,相应地考虑了一个时间单元的长度分别等于1s和60s的情形)。
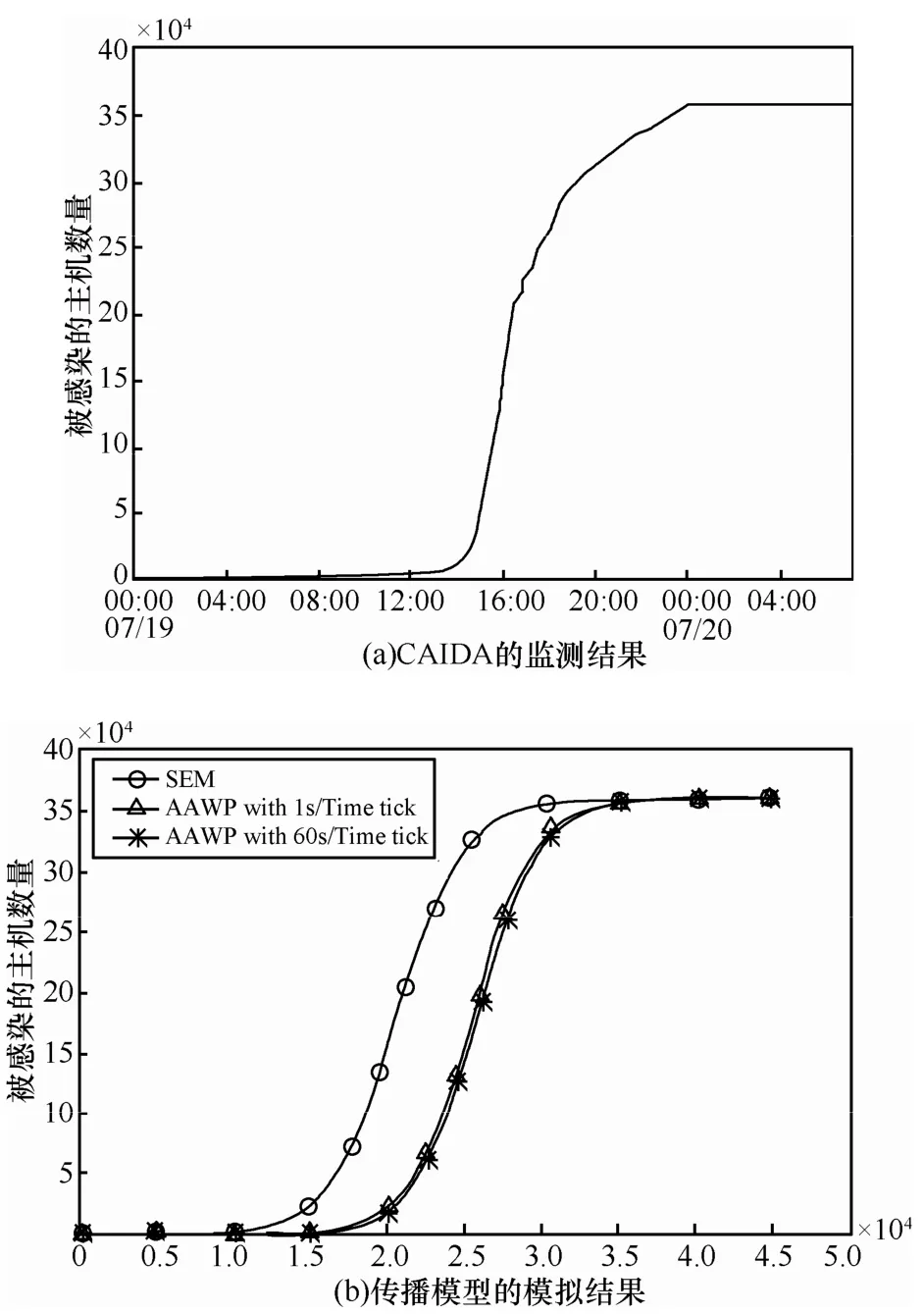
图3 Code Red蠕虫的传播曲线
从图3可以看出,对于Code Red蠕虫而言,无论是时间连续的 SEM模型,还是时间离散的AAWP模型,虽然能够大致地描述蠕虫传播曲线的总体变化趋势,但是都在不同程度上高估了蠕虫在Internet中的传播速度。例如,即使在模拟过程中取时间单元的长度等于 60s(即假设蠕虫的实例需要花费60s才能完成对某个潜在目标的感染,这在蠕虫的传播过程中已属相对罕见),AAWP模型的估算结果仍然明显超前于实际的蠕虫传播曲线。那么,又是哪些原因可能导致蠕虫在 Internet中的传播速度滞后于 SEM 或者AAWP等以同构网络假设为前提的传播模型的预期呢?下文将通过使用 Matlab来模拟Enhanced-AAWP模型,对异构的网络环境中可能影响蠕虫传播进程的部分因素进行相应的分析。
4.1 模拟参数的设置及其依据
在对分层的异构网络模型进行抽象时,Enhanced-AAWP模型假设蠕虫将在由K个相互连接的不同自治系统所组成的网络环境中进行传播。实际上,在组成IPv4地址空间的256个A类/8网络中,只有116个A类/8网络在Internet中全局路由可达[20]。因此,在模拟Enhanced-AAWP模型时,可以假设所有处于Susceptible状态的脆弱性主机均匀分布在这116个A类网络中,而在其余的140个A类网络中没有脆弱性主机的存在,从而在一定程度上反映出网络地址空间中脆弱性主机的不均匀分布。同时,在这116个分布有脆弱性主机的A类网络中,还将进一步地对每个A类网络中分别接入了1个或者2个A类的NAT子网、并且相应地分别有 7%[16]、19%或者 60%的脆弱性主机位于这些NAT子网内的情形进行模拟,从而更全面地反映出异构的网络环境中,NAT子网的数量以及脆弱性主机在 NAT子网内的密集程度等因素对蠕虫传播进程的可能影响。
虽然在模拟时只有在116个A类/8网络中分布有脆弱性主机,但是根据Code Red等绝大多数蠕虫的实际传播情况,每个蠕虫实例仍然将扫描整个IPv4地址空间,即蠕虫的扫描地址空间大小 Ω =232(如果每个蠕虫实例也将扫描地址空间优化至这116个全局路由可达的A类网络,那么这个蠕虫就将成为理论上的路由蠕虫[20])。
在扫描策略的选取上,将分别对完全的随机扫描策略、Pl= 0 .75/Pr= 0 .25的本地优先扫描策略和Pl= 0 .875/ Pr= 0 .125的本地优先扫描策略进行模拟。由于后两种本地优先扫描策略在 Pl和 Pr的取值上分别参考了Nimda蠕虫和Code Red II蠕虫的实现,因此可以将下文模拟的这两种蠕虫分别称为类Nimda蠕虫(Nimda-like worm)和类Code Red II蠕虫(CodeRed II-like worm)。
在完成的全部模拟实验中,都将取网络中初始处于 Susceptible状态的脆弱性主机数量N=359 000,蠕虫实例的平均扫描速率η=6,每个时间单元的长度为1s。
4.2 部分与NAT子网相关的因素对蠕虫传播过程的影响
图4模拟了Code Red蠕虫在脆弱性主机分布于116个A类网络、每个A类网络中各有1个A类的NAT子网,并且有19%的脆弱性主机位于NAT子网内的异构网络环境中(即 Ni′,1=(359000/116)×19%= 5 88, Ni= ( 359000/116)×81% = 2 507, 1 ≤ i≤116)进行传播的过程。为了简化后续分析的复杂性且不失一般性,模拟时将假设在每个A类网络中全局路由可达的网路区域内以及NAT子网内,都将分别有一个初始处于Infected状态的脆弱性主机(即==1, 1≤i≤116,亦即模拟环境中初始具有传染性的脆弱性主机数量I0=232)。作为对比,图4还分别绘制了当I0=232时,Code Red蠕虫和具有路由蠕虫特性的Code Red蠕虫变种在116个全局路由可达的A类网络(即在模拟环境中不考虑NAT网络的影响)中进行扫描时的传播曲线。
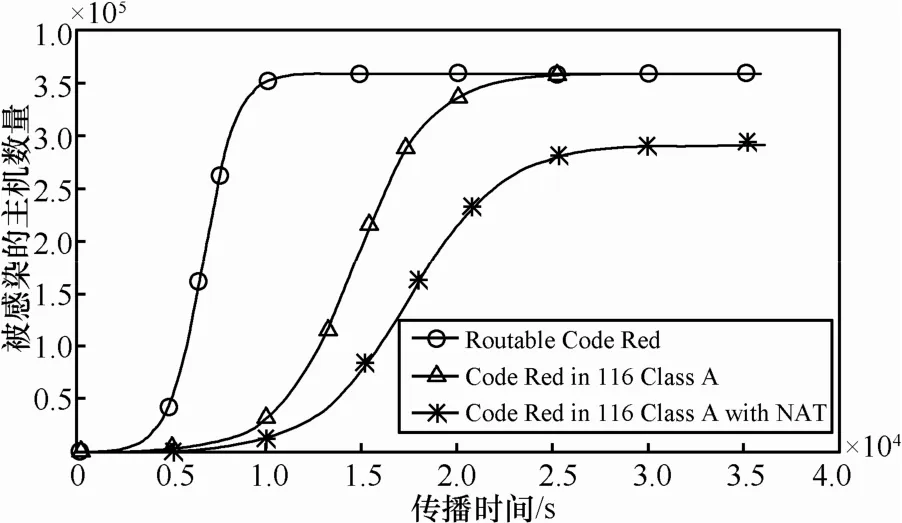
图4 异构网络环境对蠕虫传播过程的可能影响
根据图4所模拟的传播曲线可以清楚地看出,较之于同构的网络环境,当考虑了NAT子网在Internet中的使用之后,随机扫描蠕虫的传播进程出现了明显的延缓。更进一步地,图5(a)和图5(b)则相应地给出了当每个A类网络中各有1个A类的NAT子网,并且分别有7%(Ni′,1=217,Ni=2878, 1≤i ≤116)、19%以及60%(Ni′,1=1857,Ni=1238, 1≤i≤116)的脆弱性主机位于NAT子网中时,使用随机扫描策略的Code Red蠕虫和使用本地优先扫描策略的类Nimda蠕虫在扫描过程中的传播曲线(同样基于==1, 1≤i ≤116的假设)。
如图5所示,在异构的网络环境中进行传播时,无论是随机扫描蠕虫还是本地优先扫描蠕虫,随着NAT子网内脆弱性主机密度的逐步提高,蠕虫感染全部脆弱性主机所需花费的时间将逐步缩短。这是由于根据Enhanced-AAWP模型的假设,NAT子网内的脆弱性主机无法被位于全局路由可达网络区域内的蠕虫实例所感染,因此蠕虫在异构的网络环境中感染全部脆弱性主机所需花费的时间,主要取决于NAT子网内的脆弱性主机被全部感染的速度。而NAT子网内脆弱性主机的密度越高,蠕虫在NAT子网内就具有越快的传播速度。
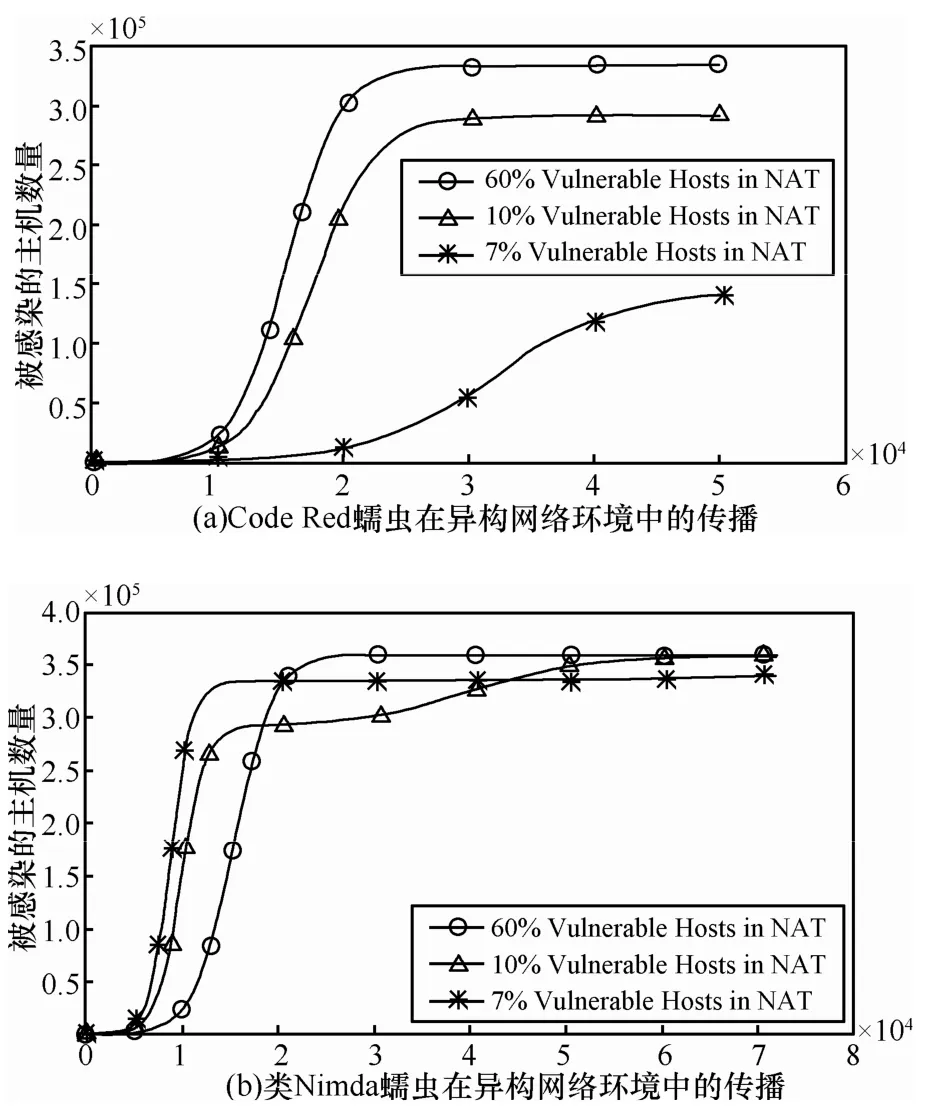
图5 脆弱性主机在NAT子网中的密集程度对蠕虫传播过程的可能影响
同时,从图5(b)中也可以看到,对于使用了本地优先扫描策略的类Nimda蠕虫,当NAT子网内脆弱性主机的密度为7%时,蠕虫在初始阶段的传播速度有可能比在NAT子网内具有更高的脆弱性主机密度(例如19%或者60%)时更快,这主要是由于此时在全局路由可达的网络区域内具有更多的脆弱性主机以及更高的脆弱性主机密度,从而使得蠕虫在全局路由可达网络区域内相对更快的传播速度对蠕虫的传播曲线造成了更大的影响。不过即便如此,当NAT子网中具有更大的脆弱性主机密度时,蠕虫将只需花费相对更少的时间即可感染网络中全部的脆弱性主机。
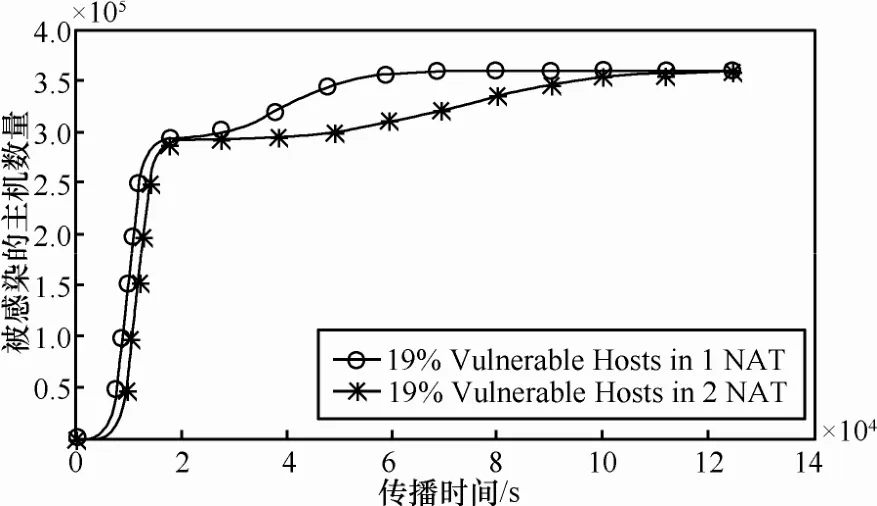
图6 NAT子网的数量对蠕虫传播过程的可能影响
图6对比了使用本地优先扫描策略的类Nimda蠕虫在19%的脆弱性主机位于NAT子网内,并且每个A类网络中分别接入了1个A类的NAT子网或者2个A类 的NAT子 网 (Ni′,1=Ni′,2=0.5× 588=294,Ni=2507, 1≤i≤116)的模拟环境中进行扫描时的传播曲线。其中,当在每个A类网络内接入了2个NAT子网时,可以假设在初始状态下,这2个NAT子网内各有一台脆弱性主机已经被蠕虫所感染,而在全局路由可达的网络区域内没有初始处于Infected状态的脆弱性主机,从而使得模拟环境中初始处于Infected状态的脆弱性主机数量可以保持相对一致(即=0,==1, 1≤i≤116)。
由于在模拟时假设每个A类网络中位于NAT子网内的脆弱性主机总量保持不变,因此NAT子网数量的增加,就意味着每个NAT子网内脆弱性主机密度的降低,从而导致蠕虫在NAT子网内的传播速度随之减缓,使得蠕虫将花费更多的时间才能完成对模拟环境中全部脆弱性主机的感染。
4.3 本地优先扫描策略的设计对蠕虫传播过程的可能影响
根据Enhanced-AAWP模型,结合相应的模拟实验,不仅可以直观地体现出与NAT子网相关的若干环境因素如何影响到蠕虫在异构网络环境中的传播过程,还可以之为基础,相应地对类似于扫描策略等在很大程度上决定了蠕虫扫描行为的内在本质特性进行深入分析。
图7(a)与图7(b)相应地对比了当模拟环境中有19%的脆弱性主机位于NAT子网内,并且在每个A类网络中分别接入了1个A类NAT子网或者2个A类NAT子网时,类Nimda蠕虫(Pl=0.75/Pr=0.25)和类Code Red II蠕虫(Pl=0.875/Pr=0.125)的传播曲线。
通过图7可以看出,具有相对更大的本地扫描概率lP的类Code Red II蠕虫在模拟环境中将表现出比类Nimda蠕虫相对更快的传播速度。这是因为无论某个蠕虫实例是位于全局路由可达的网络区域内还是某个NAT子网中,其所发出的lP扫描都还将指向自身所处的网络区域;而在其发出rP扫描中,将有部分扫描可能指向了(其他)NAT子网,或者IPv4网络中未被使用的部分地址空间(例如其余140个A类/8网络),因而未能形成实际的感染能力。同理,由于可以将随机扫描策略视为本地优先扫描策略中Pl=0的特例,因此在异构的网络环境中,本地优先扫描蠕虫应该比随机扫描蠕虫具有相对更快的传播速度,这也可以通过将图5与图7的传播曲线进行对比后得以验证。
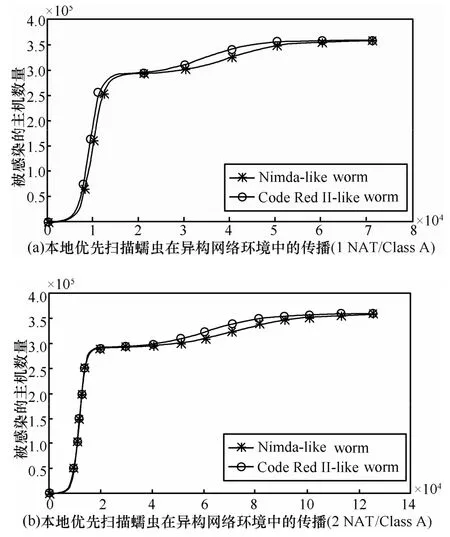
图7 本地优先扫描策略对蠕虫传播过程的可能影响
5 结束语
合理的蠕虫传播模型将有助于分析可能影响到蠕虫传播速度的多种潜在因素。本文在AAWP模型的基础上,将异构的网络环境这个外在因素纳入到传播模型的研究中,使用时间离散的确定性分析方法推导出Enhanced-AAWP模型,结合相应的模拟实验深入分析了随机扫描蠕虫和本地优先扫描蠕虫在异构网络环境中的扫描行为。在后续的工作中,将进一步地结合对异构网络环境的理解与分析,相应地完善和修订Enhanced-AAWP模型,从而更加全面、准确地反映蠕虫在Internet中的渗透传播过程,并针对性地开展蠕虫防护检测技术的研究。
[1] 卢锡城,王怀民,王戟.虚拟计算环境iVCE:概念与体系结构[J].中国科学(E辑), 2006, 36(10):1081-1099.LU X C, WANG H M, WANG J. Internet-based virtual computing environment iVCE: concept and architecture[J]. Science in China Ser E Information Sciences, 2006, 36(10):1081-1099.
[2] STANIFORD S, PAXSON V, WEAVOR N. How to own the internet in your spare time[A]. Proceedings of the 11th USENIX Security Symposium[C]. San Francisco, CA, USA, 2002.149-167.
[3] WU J, VANGALA S, GAO L X, et al. An effective architecture and algorithm for detecting worms with various scan techniques[A].Proceedings of the 11th Annual Network and Distributed System Security Symposium (NDSS’04)[C]. San Diego, CA, USA, 2004.143-156.
[4] WEAVER N, PAXSON V, STANIFORD S, et al. A taxonomy of computer worms[A]. Proceedings of ACM CCS Workshop on Rapid Malcode (WORM’03) [C]. Washington, DC, USA, 2003.11-18.
[5] ANDERSSON H, BRITTON T. Stochastic Epidemic Models and Their Statistical Analysis[M]. NewYork: Springer-Verlag, 2000.156-160.
[6] DALEY D J, GANI J. Epidemic Modelling: An Introduction[M].Cambridge, UK: Canbridge University Press, 1999.120-126.
[7] KEPHART J O, WHITE S R. Measuring and modeling computer VIrus prevalence[A]. Proceedings of IEEE Computer Society Symposium on Research in Security and Privacy[C]. Oakland, CA,USA, 1993. 2-3.
[8] FRAUENTHAL J C. Mathematical Modeling in Epidemiology[M].New York: Springer-Verlag, 1980.78-93.
[9] ZOU C C, GONG W, TOWSLEY D. Code red worm propagation modeling and analysis[A]. Proceedings of the 9th ACM Conference on Computer and Communication Security[C]. Washington, DC, USA,2002.143-148.
[10] CHEN Z S, GAO L X, KWIAT K. Modeling the spread of active worms[A]. Proceedings of IEEE INFOCOM 2003[C]. San Franciso,CA, USA, 2003.1890-1900.
[11] RAJAB M A, MONROSE F, TERZIS A. On the effectiveness of distributed worm monitoring[A]. Proceedings of the 14 th USENIX Security Symposium(Security’05)[C]. Baltimore, MD, USA,2005.15-16.
[12] SERAZZI G, ZANERO S. Computer virus propagation models[A].Tutorials of the 11th IEEE/ACM International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunications Systems (MASCOTS'03) [C]. Orlando, Florida, USA, 2003.26-50.
[13] CHEN Z S, JI C. Intelligent Worms: Searching for Preys[M].Mathematics Awareness Month: Mathematics and Internet Security Theme Essays, 2006.115-119.
[14] Distributed intrusion detection system (DShield) [EB/OL]. http://www.dshield.org/.2010.
[15] CASADO M, GANKEL T, CUI W D, et al. Opportunistic measurement: extracting insight from spurious traffic[A]. Proceedings of the 4th ACM Workshop on Hot Topics in Networks (HotNets-IV) [C].College Park, MD, USA, 2005.271-275.
[16] RAJAB M A, MONROSE F, TERZIS A. On the impact of dynamic addressing on malware[A].Proceedings of the 2006 ACM Workshop on Recurring Malcode (WORM) [C]. Alexandria, VA, USA,2006.145-153.
[17] WHITE S R. Open problems in computer virus research[A]. Virus Bulletin Conference[C]. Munich, Germany, 1998.55-66.
[18] MOORE D, SHANNON C, BROWN J. Code-Red: a case study on the spread and victims of an internet worm[A]. Proceedings of the 2nd ACM SIGCOMM Workshop on Internet Measurement[C]. Marseille,France, 2002.273-284.
[19] ZOU C C, GONG W, TOWSLEY D. On the performance of internet worm scanning strategies[J]. Journal of Performance Evaluation, 2006,63(7): 700-723.
[20] ZOU C C, TOWSLEY D, GONG W, et al. Routing worm: a fast,selective attack worm based on IP address information[A].Proceedings of the 19th ACM/IEEE/SCS Workshop on Principles of Advanced and Distributed Simulation (PADS’05)[C]. Monterey, USA,2005.178-185.

