单通道混合信号的幅度估计算法
芮国胜,徐彬,张嵩
(1. 海军航空工程学院 电子信息工程系, 山东 烟台 264001;2. 海军航空工程学院 研究生管理大队, 山东 烟台 264001)
1 引言
在无线电信号监测和侦收等非协作通信场合中,如何快速准确地获取所感兴趣信号的信号参数成为后续信号分析处理的关键环节。通常的无线电监测接收天线都是宽开的,多个信号可能同时进入接收机。对于多天线的无线电监听系统来讲,对所感兴趣的信号可以采用阵列信号处理来进行未知信号参数的估计。但是在很多特定的场合由于受限于平台空间等因素,系统只有一个接收天线(如基于微小卫星平台的PCMA信号侦收[1]、星载AIS信号探测[2]等)。因此研究单通道的多信号参数估计问题具有重要的实用意义。
由于通信信号经过信道传输到达接收端时,其信号幅度受信道衰落和噪声等因素影响发生改变,对于信号幅度的估计成为信号参数估计中的重要内容。对于单个信号幅度估计而言,主要有极大似然估计方法[3,4]、傅里叶谱分析方法[5,6]和高阶差分方法[7]等。文献[8]利用循环谱分析了干扰环境下有用信号的幅度,无需任何先验信息,能适用于低信噪比环境。相对于单个信号的幅度估计而言,单通道混合信号幅度问题的研究较少。文献[9]采用极大似然方法研究了 PCMA系统中干扰信号的幅度估计问题,但是该方法假设有用信号已知并非真正意义上的盲估计算法,不适用非协作通信场合。
混合信号的幅度参数估计是单通道信号盲分离处理的重要环节,一些现有的单通道盲分离算法需要幅度估值作为算法初始值的设置依据,但均未给出幅度估计的方法[10,11]。本文研究单通道条件下同调制方式和调制参数的MSK混合信号的幅度估计问题。将文献[8]思想扩展到单通道混合信号幅度估计中,通过MSK通信信号具有的循环平稳特性,推导了MSK混合信号的循环谱函数并据此进行分量信号的幅度估计,针对谱线选择过程中存在的谱线模糊问题,采用循环谱估计算法中的泄漏谱线包络来辅助消除谱线模糊,并通过大强度谱线位置的泄漏谱包络值来修正相应位置的循环谱幅度,以提高估计精度。仿真结果表明了该算法有效,且能够满足后续盲分离处理的需要。
2 混合信号的循环谱
假设单天线接收的混合信号由2个同调制参数的分量信号混合而成,则接收端接收到的混合基带信号可以表示成为
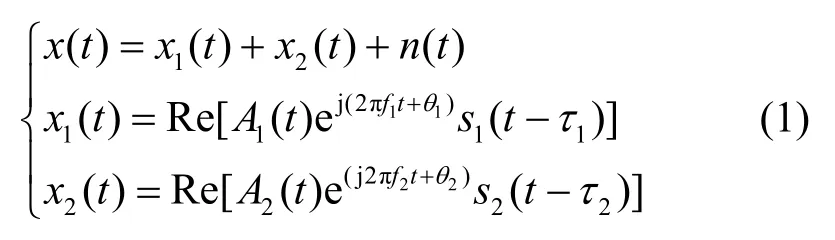
A1(t)、A2(t)为分量信号经信道传输衰减后的幅度值,f1、f2分别代表 2信号分量的载波频率偏移,θ1,θ2代表分量信号的初始相位,τ1、τ2代表信号分量的定时偏差,n(t)为 0均值的广义平稳高斯白噪声序列。当接收信号为 MSK混合信号时,s1(t)和 s2(t)可以表示成为如下形式:
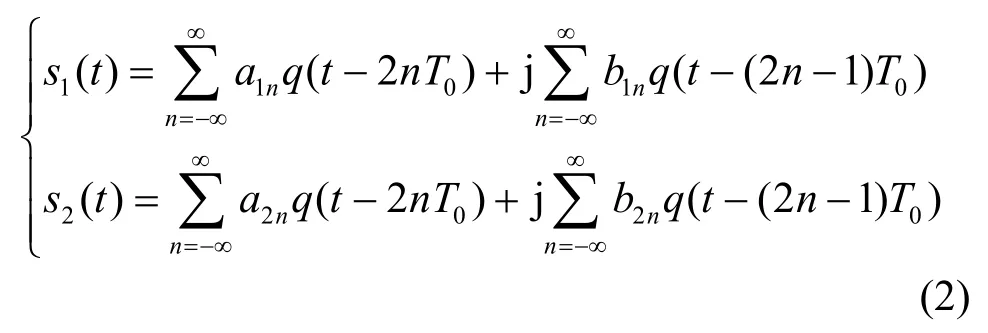
其中,a、b为二进制独立同分布的调制信息,取值为-1、1,q(t)代表调制器的相位响应函数,T0表示码元时间。
由于 MSK信号具有循环平稳特性,假设信号x1(t)、x2(t)、n(t)为零均值并且两两不相关,利用信号相加的循环谱性质可以得到如下表达式:
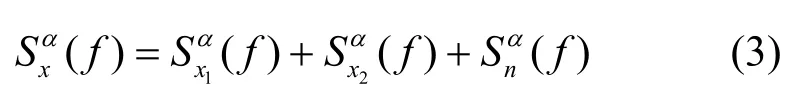
其中,α为循环频率,f代表频率。假设A1(t)、A2(t)在一个信号短突发周期内近似为常数,设为A1、A2。下面考虑单个信号分量的循环谱函数,分量信号x1(t)可以写成如下形式:
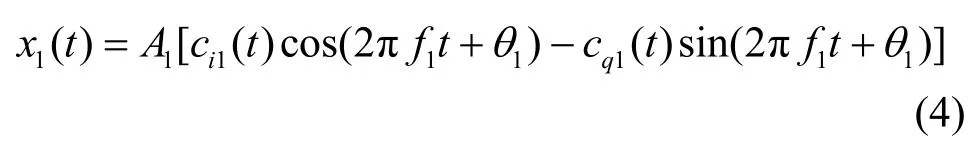
其中
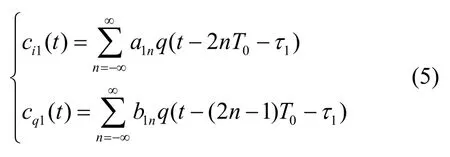
结合文献[12],可以得到分量信号 x1(t)循环谱函数为

同理,可以得到分量信号x2(t)的循环谱函数为

对于MSK信号来说,Q(f)表达式为
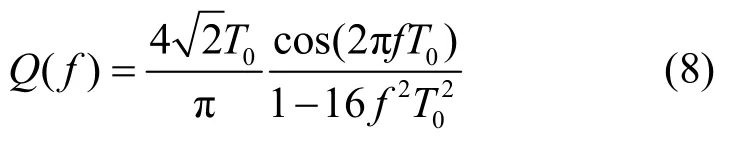
由于平稳噪声无循环平稳特性,在α≠0循环频率轴上其循环谱函数为零,则可以得到混合信号的循环谱函数为
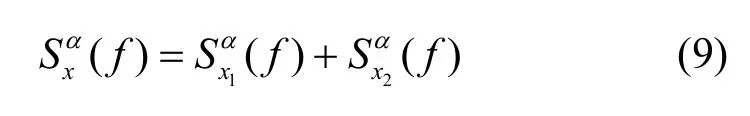
由式(6)、式(7)、式(9)可知,当混合信号分量频偏 f1和 f2不等时,在 f =0, α=±2f1±1/2T0和 f=0, α=±2 f2±1/2T0位置存在表征分量信号x1(t)和x2(t)的幅度大小的大强度的循环谱幅度值,则分量信号的幅度估计为
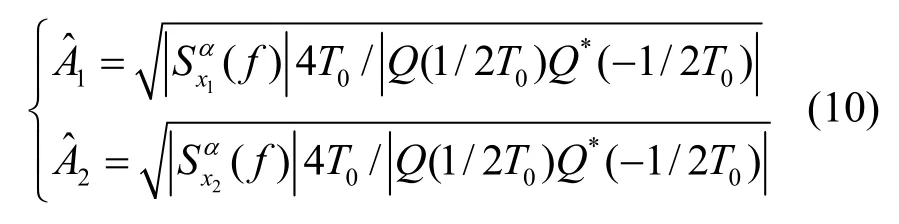
式(10)中符号间隔时间T0为未知量,由式(7)、式(8)易知在 f =0,α>0的循环频率正半轴上,在α1=2f1-1/2T0和 α2=2f1+1/2T0位置对应着分量信号x1(t)的大强度谱线,在 α3=2f2-1/2T0和 α4=2f2+1/2T0位置对应着分量信号x2(t)的大强度谱线,则T0可以用[(α2-α1)+(α4-α3)]/2 来进行估计,代入式(10)即可得到分量信号的幅度估计值。
3 谱线匹配与谱幅度修正
由前面分析可知,分量信号的幅度估计与符号间隔时间T0和大强度谱线选择有关,即与循环频率轴上 α的位置有关。在实际估计中由于没有任何先验信息,谱线位置选择会产生模糊现象,如图1所示。
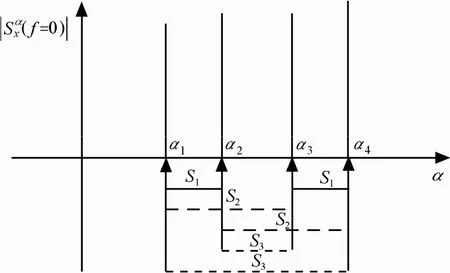
图1 谱线选择模糊
从图1中可以看出,正循环频率轴上的大强度谱线位置选择存在着3种组合形式,即S1={[α1, α2][α3,α4]}, S2= {[α1, α3][α2, α4]}, S3={[α1, α4][α2, α3]},其中只有一种正确的组合形式。这种情况称之为谱线选择模糊,把谱线选择模糊的消除称为谱线匹配。计算混合信号循环谱时,由于采用的数据量有限,得到的循环谱存在着泄漏现象[13],如图2所示。
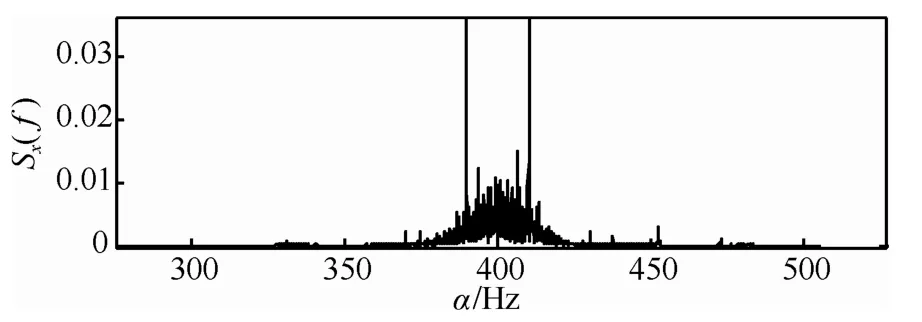
图2 单个MSK信号循环谱泄漏(f =200Hz)
从图2中可以看出,循环谱泄漏造成图形的底部明显存在着一些小的随机非零值,并且在越靠近信号载频位置其谱线强度越大,随着离载频位置距离的增加其谱线强度逐渐减弱。混合信号也存在的类似的情况,因此可以利用循环谱泄漏包络最大值点的位置来进行谱线匹配。如图3所示,当区间[α1,α2]和[α3, α4]均出现循环谱泄漏包络极大值点时,2个信号分量的强谱线分别位于α1、α2和α3、α4位置点,则选择S1谱线组合形式。如图4所示,当区间[α1, α3]和[α2, α4]出现循环谱泄漏包络极大值点时,由于组合形式S3的循环谱泄漏包络也可能出现,不能直接判断谱线的组合方式。但是由于同调制参数的MSK信号混合分量信号具有相同的码速率,谱线组合的区间长度应该相等,因此组合方式S3不会出现,此时选择S2谱线组合形式。
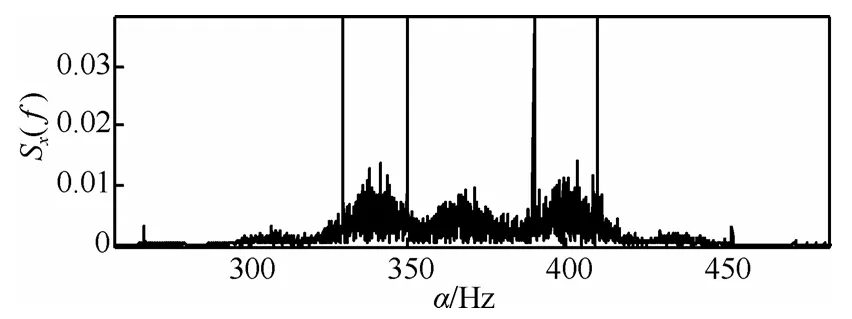
图3 S1谱线组合形式(f1=170Hz, f2=200Hz)
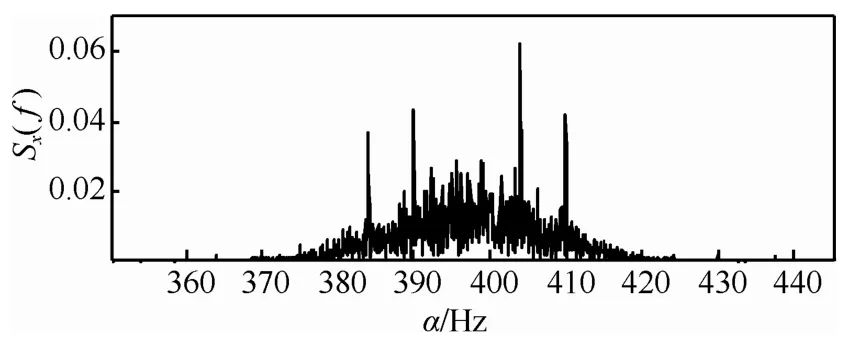
图4 S2谱线组合形式(f1=197Hz, f2=200Hz)
在实际的循环谱算法中由于数据长度有限和噪声干扰影响等因素不可避免地存在,其循环谱幅值的估计值存在着偏差,在大强度谱线的幅度估计值应该看作谱线理论幅值与噪声幅值的叠加。谱线附近的谱泄漏包络反映了泄漏谱和噪声对大强度谱线幅值的影响,因此可利用大强度谱线位置的谱泄漏包络值来修正大强度谱线的幅度,进而提高估计精度。
混合信号幅度估计算法流程如下。
1) 计算接收混合采样信号循环谱,并提取出循环谱f =0的切片中α>0的循环频率正半轴切片。
2) 搜索f =0,α>0的循环频率正半轴切片中强度较大的多条谱线,根据谱线间的相互位置,若强谱线间位置坐标相邻则只取相邻部分强度最大的1条谱线,这样保留强度最大的4条谱线,存储循环频率轴上其谱线所对应的循环频率。
3) 提取出大强度谱线循环频率族对应的频谱泄漏部分,采用k阶平滑滤波方法进行包络提取,平滑阶数k一般取感兴趣区间长度的1/16时效果较好。
4) 根据感兴趣区域包络是否存在极大值情况选取谱线组合形式,并估计符号间隔时间 T0,利用大强度谱线幅度值减去该位置点的包络幅值作为其幅度修正值,根据式(10)进行估计,分别利用分量信号 2条大强度谱线估计求均值以进一步减小误差。
4 仿真分析
为了验证前面的分析,本文采用2路MSK混合信号进行仿真实验。仿真条件设置如下:调制数据信息点个数为N=5 000个,采样率为fs=1 000Hz,码元速率为fd=20B,采用分段谱相关循环谱估计算法(SSCA, strip spectral correlation algorithm)[14],循环频率分辨率Δα=fd/512,频率分辨率Δf = fd,对每个仿真点进行100次蒙特卡洛实验,采用归一化的最小均方误差来衡量幅度的估计性能。
图5给出了当分量信号频偏之差大于符号速率时,在3种信号功率比情况下混合信号幅度估计归一化均方值随信噪比的变化情况。从图中可以看出,在信噪比SNR大于-20dB情况下,经过谱幅度修正后的估计性能要好于无谱幅度修正的估计性能,这也验证了幅度修正方法的有效性。当信噪比下小于-20dB时,由于功率比为1∶4的混合信号小功率信号受噪声影响较大,因此信号功率差异大的混合信号的估计性能下降较快;当信噪比进一步下降到-25dB以下时3种信号功率比情况下算法均产生较大误差。
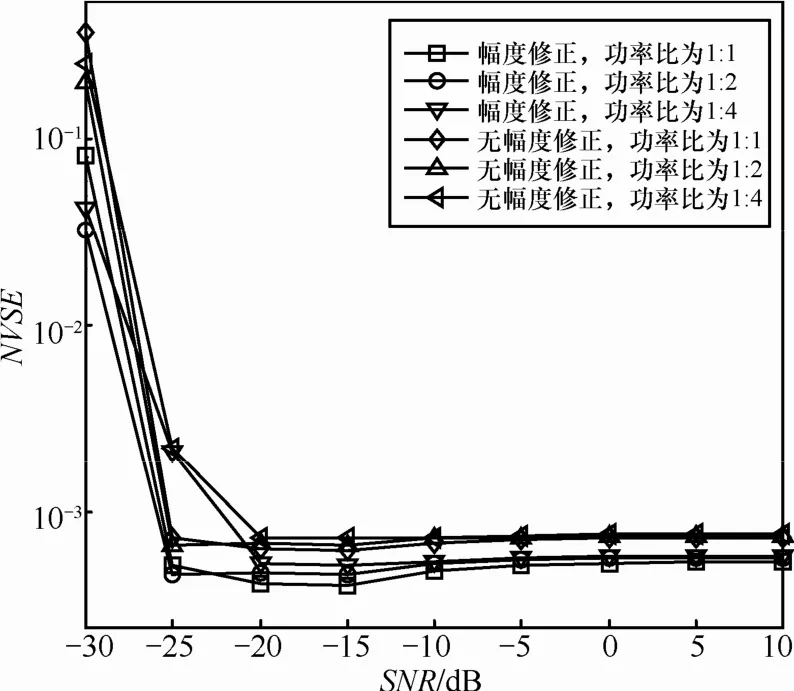
图5 幅度估计性能(f1=170Hz, f2=200Hz)
图 6给出了当分量信号频偏之差小于码速率时,在3种信号功率比情况下混合信号分量幅度估计的归一化均方值随信噪比的变化情况。从图6中可以看出:当信噪比大于-15dB时,在信号功率比为1:1和1:2条件下,算法性能趋于稳定且估计精度较高。但对于信号功率比为 1:4的情况,由于小功率信号易被大功率信号分量的谱泄漏和噪声干扰,造成谱线判断发生错误,致使估计误差较大。另外,经过幅度修正后的估计精度要明显高于未经幅度修正的情况,并且在干扰相比于图5中情况较大的情况下幅度修正的效果更明显。
结合图5和图6可以得出对等功率信号分量的幅度估计精度要高于功率不对等的情况,主要是小功率信号相对来说更易受到噪声和循环谱泄漏的干扰,从而致使估计性能下降。另外,在频偏之差小于码速率的情况下,由于信号分量之间的循环谱除了受信号分量各自循环谱泄漏和噪声影响外还要受两者的相互干扰影响,因此其幅度估计精度要低于频偏之差大于码速率的情况。
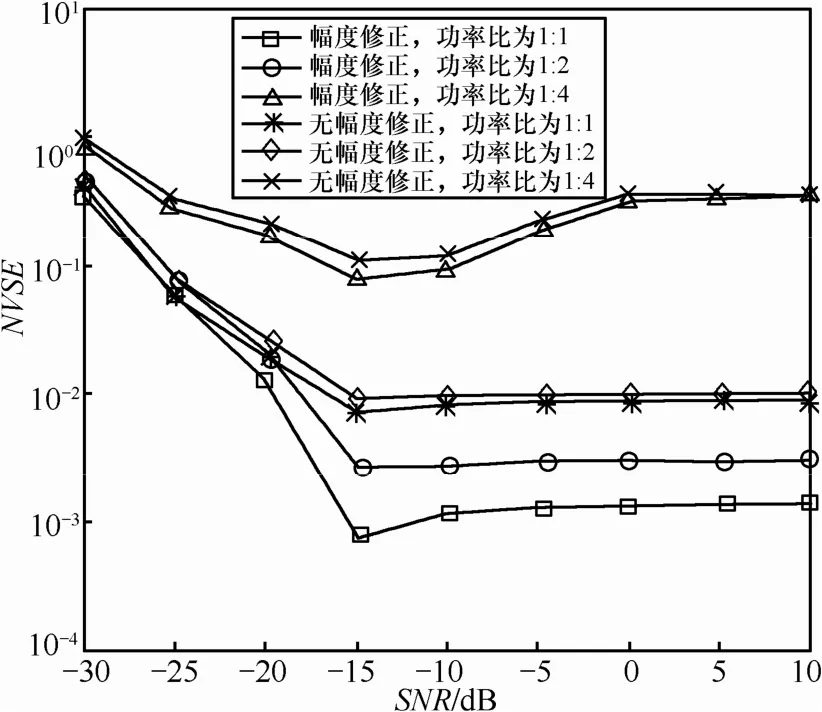
图6 幅度估计性能(f1=197Hz, f2=200Hz)
本文算法的计算量开销主要是由循环谱估计的计算量决定的,在此仅分析本算法采用的分段谱相关算法的计算复杂度。由SSCA循环谱估计算法主要分 3步实现[15]:1) 计算解调复包络信号,利用一个N'点FFT实现,N'为数据加窗长度;2) 计算复包络与实信号的共轭相关,为一个N'/2的乘法阵;3) 最后求N'/2个N点FFT组成的变换阵。其各步实现的运算量如表1所示。从表1中可以看出SSCA循环谱估计算法的计算复杂度较高,但在实际工程中可以采用其改进算法,并采用并行处理的方式以提高其运算速度,能够满足实时性处理的需要[16]。

表1 SSCA算法复杂度
5 结束语
本文研究单通道条件下同调制方式和调制参数混合信号的参数估问题,给出了一种基于循环谱的混合信号幅度估计算法。仿真表明了该算法的有效性,其估计精度能够满足后续信号的处理需要,具有实用价值。
[1] MARK D. Paired carrier multiple accesses (PCMA) for satellite communications[A]. Pacific Telecommunications Conference[C].Honolulu, Hawaii, 1998.
[2] TORKILD E, GUDRUN H, BJORN N. Maritime traffic monitoring using a space-based AIS receiver[J].Acta Astronautica, 2006, 58(10):537-549.
[3] 杨学贤, 张群英, 韩月秋. 欠采样下的信号幅度估计[J].通信学报,1999, 20(12A): 318-322.YANG X X, ZHANG Q Y, HAN Y Q. Signal amplitude stimation with under-sampling rate method[J]. Journal of China Institute of Communications,1999, 20(12A): 318-322.
[4] COLLMEYER A J, GUPTA S C. Estimating the amplitude of a sinusoid from noisy random samples[J]. IEEE Transactions on Information Theory, 1970, 6(4): 488-489.
[5] HUANG X D, WANG Z, HUO G Q. New method of estimation of phase, amplitude, and frequency based all phase fft spectrum analysis[A]. Proceedings of 2007 International Symposium on Intelligent Signal Processing and Communication Systems[C]. Xiamen, China,2007. 284-287.
[6] 齐国清, 贾欣乐. 基于DFT相位的正弦信号幅度估计[J]. 大连海事大学学报, 2001, 27(3):71-74.QI G Q, JIA X L. High accuracy amplitude estimation of sinusoid based on the phase of DFT[J]. Journal of Dalian Maritime University,2001, 27(3): 71-74.
[7] WU J K, LONG J, LIANG Y. Estimation of frequency, amplitude and phase of sinusoidal signals[A]. IEEE 2004 International Symposium on Industrial Electronics, Palais des Congres Ajaccio[C]. 2004.353-356.
[8] LEOPOLDO A, ANTONIO N. True-power measurement in digital communication systems affected by in-channel interfernce[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(12):3985-3994.
[9] 潘申富, 白栋, 依那等. 成对载波多址系统中干扰信号幅度的估计[J]. 真空电子技术, 2003, 21(2): 21-24.PAN S F, BAI D, YI N, et al. Estimation of interference amplitude in PCMA system[J]. Vacuum Electronics, 2003, 21(2): 21-24.
[10] LIU K, LI H, DAI X, et al. Single channel blind separation of cofre-quency MPSK signals[A]. Proceedings of Communications, Internet and Information Technology[C]. 2006.42-46.
[11] TU S L, ZHENG H, GU N. Single-channel blind separation of two QPSK signals using per-survivor processing[A]. IEEE Aisa Pacific Conference on Circuits and Systems[C]. 2008. 473-476.
[12] VUCIC D, OBRADOVIC M. Spectral correlation evaluation of MSK and offset QPSK modulation[J].Signal Process, 1999, 78(3):363-367.
[13] JEROME A. Cyclic spectral analysis in practice [J]. Mechanical Systems and Signal Processing, 2006, 21(2): 597-630.
[14] BROWN W, LOOMIS H. Digital implementations of spectral correlation analyzers[J]. IEEE Transactions on Signal Processing, 1993, 41(2):703-720.
[15] 马国宁. 高效循环谱估计算法的研究及其应用[D]. 成都:电子科技大学硕士学位论文, 2006.MA G N. Research on Efficient Cyclic Spectrum Estimating Algorithm and Its Applications[D]. Chengdu: Master Dissertation of UEST, 2006.
[16] 高玉龙, 张中兆. SSCA算法改进及实现[J]. 哈尔滨工业大学学报,2008, 40(9): 1374-1377.GAO Y L, ZHANG Z Z. Modification and implementation of SSCA algorithm[J]. Journal of Harbin Institute of Technology, 2008, 40(9):1374-1377.

