基于MATLAB的ASR模糊控制仿真研究＊

李发均 王亚军 董雅丽 李家强

（空军雷达学院黄陂校区1） 武汉 430345）（95859部队2） 酒泉 753000）（空军雷达学院五系3） 武汉 430019）

1 引言

MATLAB提供的动态系统仿真工具SIMULINK，有效地解决了仿真技术中的许多问题，使仿真建模变得非常方便，只需修改仿真参数，即可直观地看到显示结果[1]。本研究利用MATLAB／SIMULINK建立1／2摩托车仿真模型，并采用软件中的Fuzzy logic toolbox对模型进行施加模糊控制，最后进行单一高附着系数路面起步加速仿真模拟。

2 系统建模

2.1 单轮车辆模型

为了简化研究问题，采用单轮车辆系统模型，如图1所示[2]。忽略空气阻力和车轮的滚动阻力，可以得到下列方程组：

车辆运动方程：

车轮运动方程：

车轮纵向摩擦力：

式中，M为车辆质量；v为车辆速度；Fμx为车轮摩擦力；I为车轮转动惯量；R为车轮转动半径；ω为车轮角速度；μx为纵向附着系数；Fz为车轮对地面法向反力。

2.2 动力模型

对于车辆动力系统是很复杂的系统要准确描述是非常困难的，在本文就发动机的动力图和驾驶员在实际起步加速时的动作进行一个简化建立一个数学模型[3]。

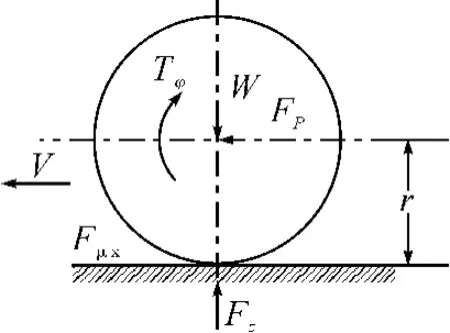
图1 单轮车辆系统模型

摩托车JH150T的标定功率为8.1kW，根据驾驶员的驾驶经验将动力模块的节气门开度描述为一个指数曲线变化的参数：

外特性功率曲线拟合为一个指数曲线：

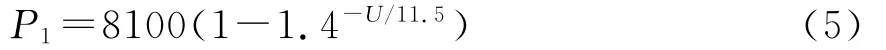
而节气门开度和部分功率与外特性功率之间的关系由理论拟合为：

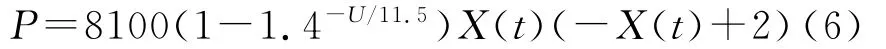
在5s内功率达到标定功率的80%左右。这是比较符合实际情况的过程。之后一直趋近标定功率。而驱动扭矩和驱动轮的转速的关系：

其中：P为驱动功率（W），U为驱动轮的转速（rad／s），T为驱动扭矩（n.m），t为时间（s），X为节气门开度。

2.3 制动器模型

对于盘式制动器，摩擦制动力矩与制动油泵压力之间的关系可以表示为[4]：

式中，Mφ为摩擦制动力矩，p为制动油泵压力，s为制动油缸活塞面积，φ为制动块与制动盘之间的摩擦系数，re为制动盘有效半径。

3 系统实现

3.1 车辆驱动动力学模块

ASR车辆驱动动力学模块如图2所示。

在车辆动力学模块中输入量In1为当前车轮滑动率状态下所对应的附着系数。模型中的各参数如下：m为车辆的质量；Rr为驱动车轮的半径。

ASR车辆动力学模块的作用：通过对输入信号In1的计算，可以得到当前车轮向前的轮胎力矩、车辆的速度及驱动距离；并将轮胎力矩与压力调节执行机构得出的当前制动力矩还有动力模块得出的驱动扭矩比较后得到车轮角速度；将车辆的速度及制动距离输入到workspace中；同时当检测到车速为13.8m／s时，发送仿真结束信号。

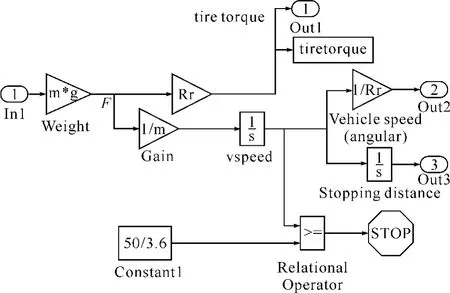
图2 ASR车辆驱动动力学模块

3.2 ASR模糊控制器

本系统为基于车轮滑移率／滑动率的模糊控制系统[6]，其所涉及的精确量的模糊化有三个量：实际滑动率与目标滑动率的偏差即滑动率误差Es、误差变化率Ex及制动力矩增量U。如图3所示。

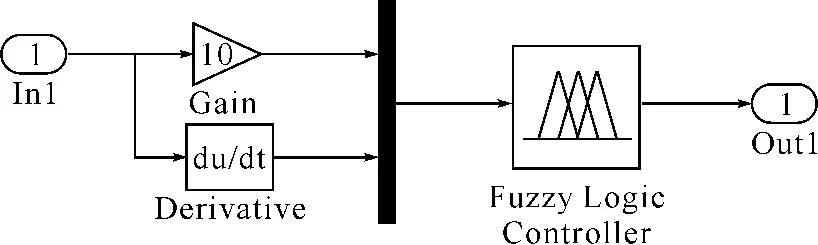
图3 ASR模糊控制器

3.3 ASR动力模块模型

ASR动力模块模型是模拟摩托车起步加速时的驱动轮上的动力状况，功率是一个指数变化的变量它无限趋近标定功率。轮速和驱动扭拒的乘积是功率，这样在任何时刻通过功率模型得出此时的功率，再由此时的轮速计算出此时的驱动扭矩。从而为下个采样循环提供驱动力。如图4所示。

图4 ASR动力模块

4 仿真及其结果

为了分析基于滑动率的控制算法的有效性，对JH150T的后轮进行单个车轮的仿真计算。所需的参数：标定功率为8100W；最高车速95km／h；模拟车轮垂直载荷Fn＝612.5N，整车重量为1250N；车轮转动惯量J＝5.8906kg／m2；制动器扭矩变化率a＝4000Nm／s；起步加速初速度v＝0km／h，仿真结束速度为50km／h。仿真模型选择固定步长，其值为0.02s。在计算机上对摩托车进行以初速度为0km／h（即v0＝0m／s）时，在单一干燥混凝土路面（最佳滑动率s＝0.2）直线起步加速过程的仿真。仿真的整体示意图如图5所示。

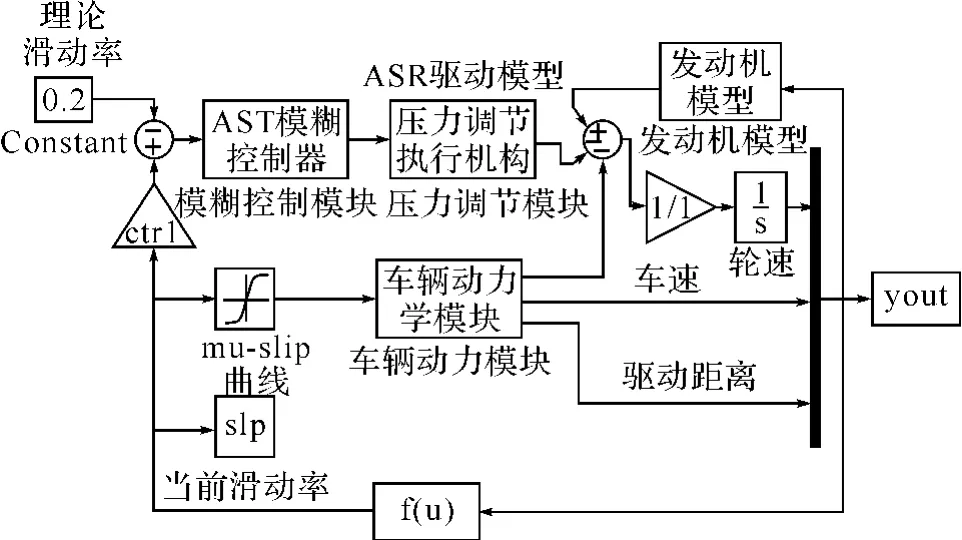
图5 ASR仿真框图

这是起步加速仿真过程的结果，初始车速为0m／s，初始轮速为1rad／s。仿真结束标志是车速为13.8m／s。

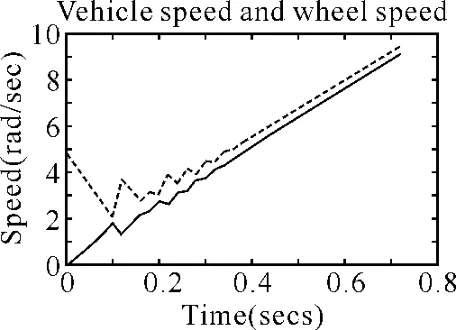
图6 车速轮速仿真结果

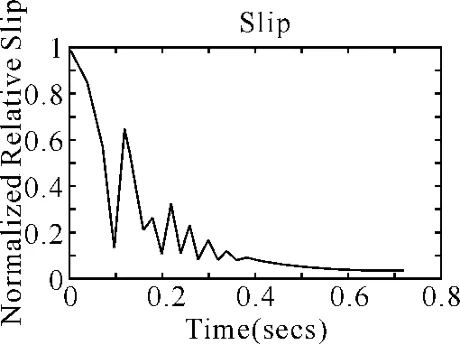
图7 滑动率仿真结果

如图6和图7所示，可以看出真正ASR起作用的时间段是在起步的起始阶段0.5s内。在之后的时间里ASR的调节作用没有体现出来。这一段时间就是普通的驱动过程。车速跟随轮速的过程。滑动率基本保持在一点上，低于最佳滑动率。在ASR实际起作用的时间内，起始时刻在离合器刚接合时车轮接受到冲击的一定动量。在很短时间内获得较小的轮速4.8860rad／s，由于车辆的惯性相对较大，起始的车速为0。所以在起始阶段滑动率基本接近1。经过在mu－slip曲线里查出此时的实际利用的附着系数，给动力学模块从而得出此时的轮胎力矩、车速和驱动距离。再加上由模糊控制器得出的制动压力的调节值经过压力调节器的迟滞之后得出此时的实际制动力矩，与动力模块的驱动扭矩比较得出此时的轮速，为下个滑动率的计算奠定了基础。这样一个个循环的继续仿真下去直到车速为10km／h，满足stop条件，终止仿真。

[1]姚俊，等.Simulink建模与仿真[M].西安：西安电子科技大学出版社，2002，8

[2]潘为民.摩托车制动防抱死控制ECU及其数据采集系统的开发[D].北京航空航天大学硕士论文，2003

[3]余志生.汽车理论[M].第二版.北京：机械工业出版社，1998

[4]程军.防抱死制动系统不同控制方法的模拟研究[J].汽车技术，1998（8）：1～7

[5]怯肇乾，宋现超.嵌入式模糊智能控制系统设计[J].计算机与数字工程，2009，37（6）

[6]张代胜，等.基于滑移率的汽车防抱模糊控制算法与仿真[J].农业机械学报，2002，33（2）