一种有向概率图连通性仿真算法＊

马 睿 朱建冲

（海军工程大学管理工程系 武汉 430033）

1 引言

图论是一门很有实用价值的学科，近年来它受计算机科学蓬勃发展的刺激，发展极其迅速，应用范围不断拓广，已渗透到诸如运筹学、逻辑学、物理学、以及数学的其它分支中[1]。特别在运筹学中，在系统效能评估[2]、故障诊断[3]、系统可靠性分析[4]、路径优化[5]等方面均扮演着重要的角色。图的连通性是图论里的一个重要问题，许多人对图的连通性算法进行了研究。陆鸣盛[6]等提出一种改进的蒙特卡罗法对图的连通性进行分析，由于蒙特卡罗法是一种随机抽样算法，其精度取决于采样的数量，当网络规模较大结构复杂时，采样数量十分庞大，并且计算精度受到影响。厉海涛[7]等总结了贝叶斯网络推理的一些方法，黄晶[8]等创造性地将贝叶斯网络应用于路网失效的评估中，尹洪英[9]等使用贝叶斯网络对公路网脆弱性路段的识别进行了研究。上述基于贝叶斯网的连通性研究具有理论上的严格性和一致性，然而也存在许多不足，如处理多连通问题方法复杂，采用条件概率数据之间存在依赖性等。本文提出一种计算图连通性的精确方法，图上各条边的连通性是相互独立的，适用于多连通问题的分析。由于是精确计算，避免了近似计算中数量庞大的采样运算，并且可以直接得出各条边不连通时整个网络连通的概率以及灵敏度分析结果。

2 基本理论与思路

2.1 基本理论

分析有向图的连通性，首先要找到连接指定起始点的最小路集合。邻接终点矩阵法[10]是求最小路集合的有效方法。在已知各条边连通概率、整个网络连通概率以及当各条边失效时网络连通概率的基础上，根据贝叶斯概率公式可以求得网络不连通时各边失效概率。

2.2 算法思路

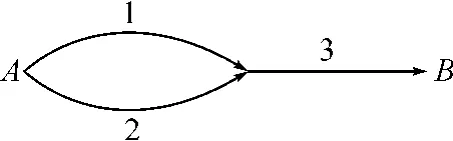
图1 有向概率图结构1

假设一个由3条边组成的有向概率图如图1所示。

边1、2、3连通的概率分别为0.6、0.7、0.8，各边连通情况与路AB连通情况关系及概率如表1，其中1代表连通，0代表不连通。

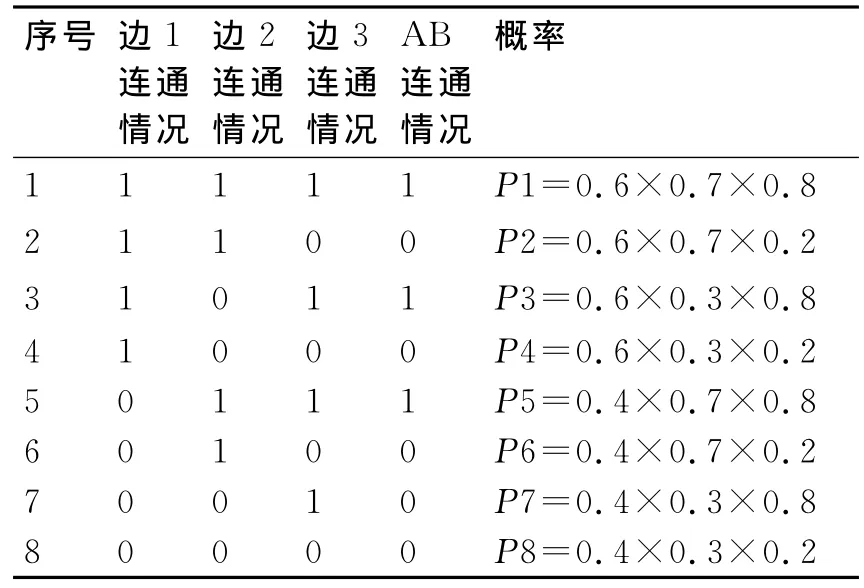
表1 各边连通情况与路AB连通情况关系及概率

AB连通的概率为P＝（P1＋P3＋P5）／（P1＋P2＋P3＋P4＋P5＋P6＋P7＋P8）＝0.704

GENIE是匹兹堡大学开发的一款计算概率图的软件，可根据上述算法思想进行网络连通性分析。本文的算法首先通过用MATLAB编程，对有向概率图进行初步计算，将所得中间结果输入到GENIE中，就可以对有向概率图的连通性进行比较全面而且精确的分析。

3 仿真算法

3.1 编码方案

3.1.1 最小路集矩阵S

对于一个有n条边、m条最小路的最小路集合，产生m条长度为n的0－1编码，每条编码中1的位置表示该条最小路上包含该条边，否则该位置为0，从而产生一个元素值为0或1的最小路集合矩阵。例如，对于最小路集合[R1R4，R2R5，R1R3R5]，其最小路集合矩阵为：

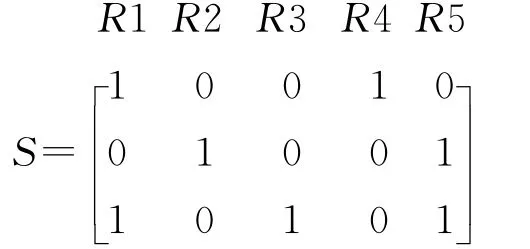
3.1.2 网络连通分布码t

对于有n条边的最小路集合，产生一个长度为2n的0－1数组，每一位数字代表了n条边通断情况下整个网络的通断情况，0为不连通，1为连通。称该数组为该最小路集合的网络连通分布码。最小路集合[R1R4，R2R5，R1R3R5]的网络连通分布码如图2所示。

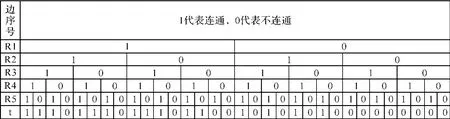
图2 网络连通分布码

3.2 步骤与实现

3.2.1 步骤

1）使用邻接终点矩阵法求有向概率图的最小路集矩阵。

2）使用MATLAB编程，以最小路集矩阵为输入，计算最小路集中各个边通断情况下整个网络连通的情况即网络连通分布码t。

3）将步骤2）中的网络连通分布码输入GENIE软件，得到整个网络连通的概率以及各个边失效时整个网络失效的概率。

4）根据步骤3）的结果，结合条件概率公式（贝叶斯公式），计算整个网络失效时各边失效的概率。

5）进行灵敏度分析。

3.2.2 计算网络连通分布码t的MATLAB流程

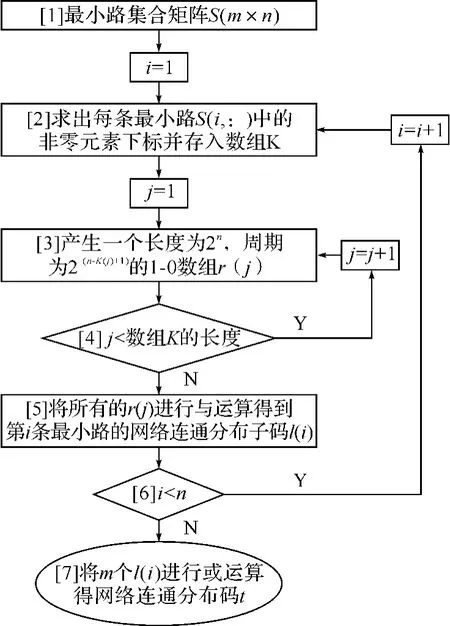
图3 计算网络连通分布码的流程

下面结合计算流程框图对其基本执行过程给出详细解释：

Step1：将最小路集合矩阵S（S为m×n矩阵）作为初始条件输入程序；

Step2：对于第i条最小路，将最小路矩阵第i行中值为1的元素的下标存入数组K；

Step3：对于数组K的第j个元素，产生一个长度为2n，周期为2（n－K（j）＋1）的1－0数组r（j）；

Step4：判断是否对数组K的所有元素都进行了Step3的计算，如果是进入Step5，否则返回Step3；

Step5：将得到的第i行所有值为1的元素的r（j）进行与运算，得到第i条最小路的网络连通分布子码l（i）；

Step6：判断是否对全部的最小路都计算了l（i），是则进入Step7，否则返回Step2；

Step7：对全部最小路的网络连通分布子码l（i）进行或运算，得到网络连通分布码t。

4 算例

在CPU为Pentium1.6G，内存1G的计算机平台上分析本文的算法。

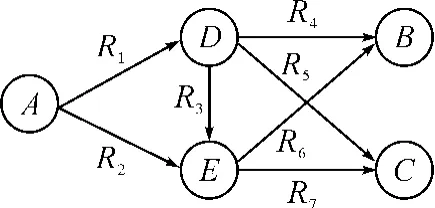
图4 有向概率图结构2

一个由5个点7条边组成的有向概率图，结构如图4所示。

各边的失效概率如表2所示。

表2 各边失效概率

A到B的最小路有3条，分别是[R1，R4]，[R2，R6]，[R1，R3，R6]，表示为最小路矩阵：

将最小路集矩阵SAB输入到MATLAB程序，计算得到：

tAB＝[1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0]，用时0.113s。

A到C的最小路有3条，分别是[R1，R5]，[R2，R7]，[R1，R3，R7]，表示为最小路矩阵：

将最小路集矩阵SAC输入到MATLAB程序，计算得到：

tAC＝[1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0]，用时0.105s。

A到B和A到C同时连通的情况有9种，分别是：

[R1，R4，R5]，[R1，R2，R4，R7]，[R1，R3，R4，R7]，[R1，R2，R5，R6]，[R2，R6，R7]，[R1，R2，R3，R6，R7]，[R1，R3，R5，R6]，[R1，R2，R3，R6，R7]，[R1，R3，R6，R7]，表示为最小路矩阵：

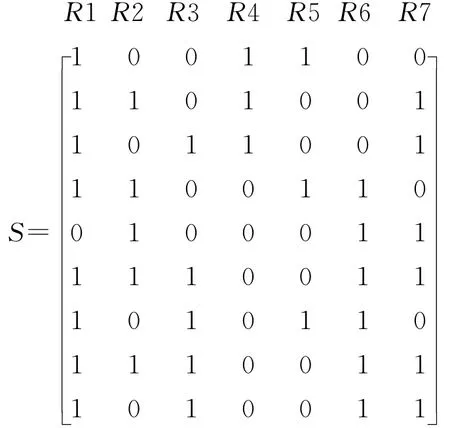
将最小路集矩阵S输入到MATLAB程序，计算得到：

t＝[111111101100110011111010110010001111111 0110011001111000000000000100010001000100010 0010001000100000000000000000000000000000000000]，用时0.521s。

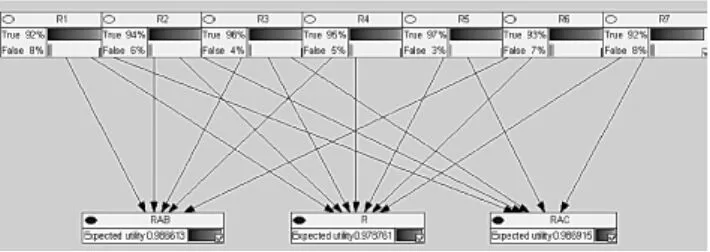
图5 网络连通概率

将7条边失效的概率以及tAB、tAC、t输入到GENIE2.0得到结果如下：

1）A到B连通的概率为0.986613，A到C连通的概率为0.986915，A到B、C同时连通的概率为0.978761。

2）各边失效时网络连通概率

将R1设置为证据变量可以得到当R1失效时A到B，A到C及A到B、C连通的概率。

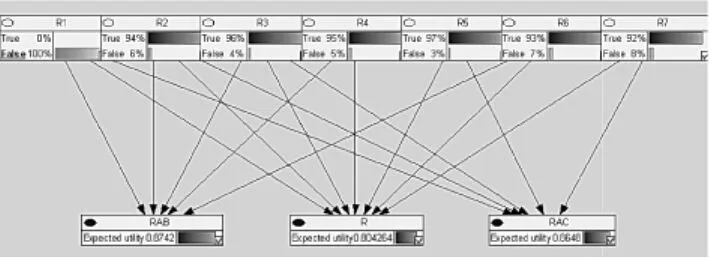
图6 R1失效时网络连通概率

同理可得到R2、R3、R4、R5、R6、R7失效时网络的连通概率，结果如表3所示。

3）根据贝叶斯公式，计算A与B、C不能同时连通时，各条边失效的概率，结果如表4所示。

表3 各边失效时网络连通概率

表4 网络不连通时各边失效的概率

4）灵敏度分析

给R1一个扰动使其连通概率在0.88，0.92，0.96三种情况间变动得到灵敏度分析结果如下：

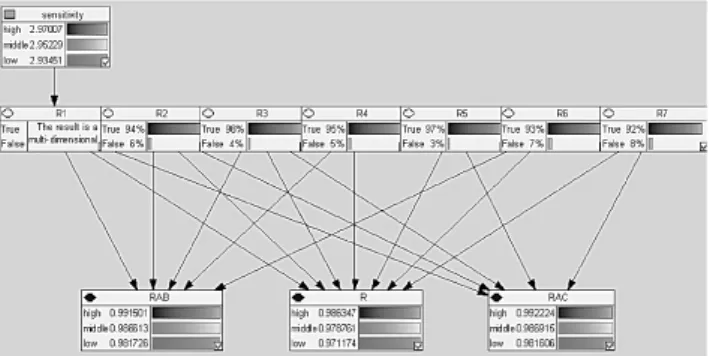
图7 R1灵敏度分析结果

在R1连通概率为0.96，0.92，0.88的情况下R，RAB，RAC连通概率如表5所示。

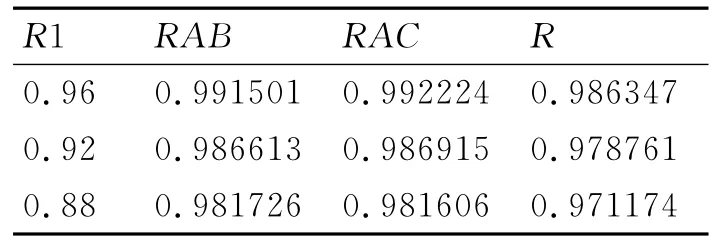
表5 R1灵敏度分析结果

结果表明该方法精度准确，运算速度快，适用于复杂结构的有向概率图连通性分析。

5 结语

图论中的网络连通性具有重要的研究价值，当前对网络连通性的分析方法大多侧重于近似计算和基于条件概率的因果推理。本文从网络的基本结构出发，提出一种网络连通性的仿真算法，该算法具有计算结果精确、计算数据相互独立的特点，适用于结构复杂的网络系统，可以计算出证据变量的后验概率并进行灵敏度分析，对网络连通性的分析比较全面。

[1]卜月华，吴建专，顾国华，等.图论及其应用[M].南京：东南大学出版社，2000：1～3

[2]秦前付，曹存根，徐洸.基于图论的作战计划军事效果评估[J].计算机科学，2005，32（7）：148～151

[3]王宝龙，徐赫，苏林，等.图论方法在装备测试与诊断信息建模中的应用[J].弹箭与制导学报，2008，28（4）：241～244

[4]束洪春，刘宗兵，朱文涛.基于图论的复杂配电网可靠性评估方法[J].电网技术，2006，30（21）：46～49

[5]王朋振，张长根，孔凡成，等.军品配送网络优化方法的比较研究[J].物流技术，2010（Z1）：209～211

[6]陆鸣盛，沈成康.图的连通性快速算法[J].同济大学学报，2001，29（4）：436～439

[7]厉海涛，金光，周经伦，等.贝叶斯网络推理算法综述[J].系统工程与电子技术，2008，30（5）：935～939

[8]黄晶，徐丽群.基于贝叶斯网络的路网失效程度评估方法研究[J].科学技术与工程，2010，10（9）：2127～2133

[9]尹洪英，徐丽群.基于贝叶斯网络的路网脆弱路段识别模型[J].系统管理学报，2010，19（6）：656～661

[10]袁亚华，王自果.最小路集的邻接终点矩阵算法[J].西北工业大学学报，1989，7（4）：473～477