水下接收罗兰C信号周期识别补偿方法研究＊

吴绳正 刘敬虎 朱银兵 李 豹

（海军司令部航海保证部1） 天津 300042）（91576部队2） 宁波 315021）

（海军工程大学电气与信息工程学院3） 武汉 430033）

1 引言

目前用于水下通信的主要是甚低频波段，但是该频段尚不具有导航与定位功能，罗兰C系统是一种远程无线电导航系统，工作于长波波段，信号具有一定的透水能力，具备水下定位与导航的潜能，研究罗兰C信号的水下导航与定位具有重要意义。但是，由于水对电磁波传播的色散效应相对空气强得多，罗兰C信号在水下传播时的信号幅度会大幅度衰减，各频率分量在经过相同路径传播后的相位改变量并不相同。因此，随着深度的增加，水下接收到的罗兰C信号包络形状在不断地发生变化，利用空气中的标准半峰值比进行周期识别将会产生识别错误，需要进行包周差补偿以提高定位精度。在罗兰C信号的周期识别方面，国内外已经有大量的学者进行了相关研究，如 Mohammed[1～3]等结合不同的谱估计方法分析了基于IFFT频谱相除的天地波识别方法；胡东亮[4～5]分析了基于 MUSIC算法的天地波识别方法；周新力等利用多项式求根方法替代MUSIC算法中的谱搜索提出了新的天地波识别算法[6]；笔者也在前期研究了二次IFFT频谱相除识别天地波的方法[7]以及基于时频分析的周期识别方法[8]，上述方法各具优点，但运算量都较大，比较复杂，而且在水下接收罗兰C信号的周期识别中同样需要进行包周差补偿处理。为此，本文将在分析罗兰C信号水下传播色散特性基础上，采用最小均方设计思想，设计一种能够克服色散效应影响，既融入包周差补偿，又简单可行的用于水下接收罗兰C信号识别的周期识别方法。

2 罗兰C信号水下色散特性

罗兰C信号的工作频段主要集中在90～110kHz，可以看成由多个频率分量正弦波按照一定幅度与相位叠加而成的。在空气中，不同频率分量正弦波的传播速度均为光速，空气对各频率分量的衰减相同，因此，在空气中距离发射台一定距离接收到的罗兰C信号波形是各频率分量的同相叠加。而罗兰C信号透过水面向下传播时，由于水（海水或淡水）是一种色散介质，对不同频率的正弦波传播速度不相同，因此，在水下一定深度接收到的罗兰C信号波形是由上述频率分量按照不同的衰减幅度与相位叠加而成的，合成信号的包络将会发生变化，在水下接收信号实现正确搜索与跟踪的前提下，必然要求在信号的周期识别过程中进行包周差补偿，否则将会导致周期识别错误，定位结果不可用。

为了分析罗兰C信号入水后的色散特性，根据信号分析理论，设数字化后罗兰C信号x（n）的样本长度为N，则由DFT变换有

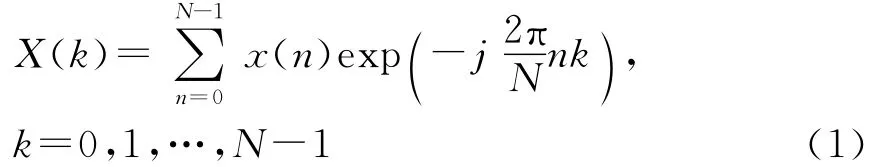
复数序列X（k）对应频率分量的幅度和相位可分别表示为

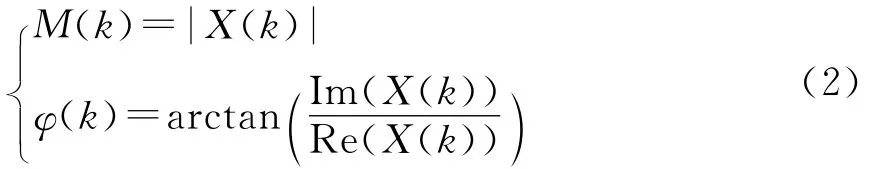
根据电磁波传播理论，假设频率分量k的信号在入水深度L后的幅度衰减为Δm（k），相位偏移为Δn（k），则频率分量k的信号在水深L处可表示为

将式（3）得到的各频率分量信号X（k）′进行合成即可得到水深L处接收到的罗兰C信号频谱，然后对其进行傅里叶逆变换即可得到水深L处接收到的罗兰C信号时域波形：

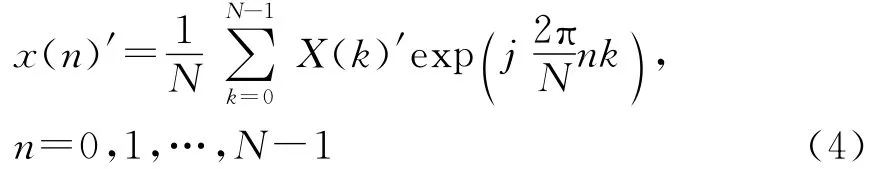
在此基础上，本文在采样率为100M，数据长度为30000，海水媒质中的电导率取σ＝4，淡水中的电导率取σ＝0.03的条件下，对罗兰C信号在水下（海水或淡水）不同深度时的色散效果进行了仿真，结果分别如图1与图2所示，其中图1为海水中不同深度的色散结果，图2为淡水中不同深度的色散结果。

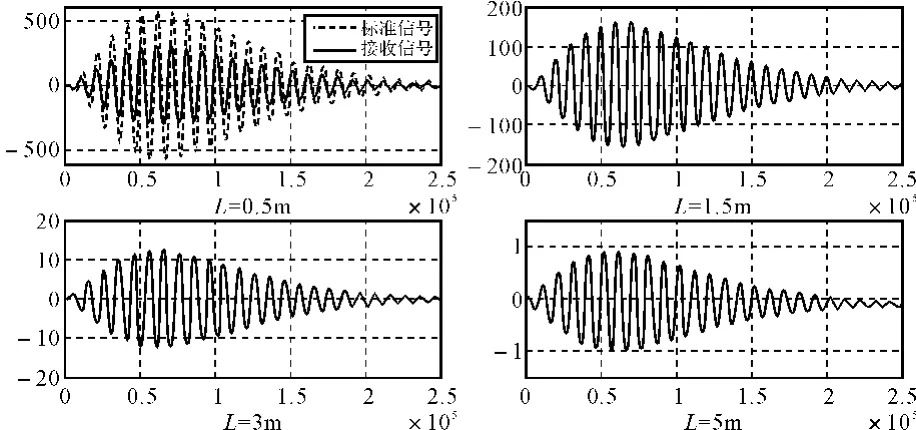
图1 不同深度海水中色散波形

图2 不同深度淡水中色散波形

由图可见，罗兰C信号在穿透海水（或淡水）后，不仅信号幅度发生较大衰减，信号相位也发生了变化，导致信号包络发生了形变。因此，进行信号周期识别时需要进行包周差补偿，为此，本文对水下（海水或淡水）不同深度时域信号的前五周半峰值比进行了统计，结果分别如表1、表2所示。

由表中可知，在海水中2m以下深度时，色散对罗兰C信号波形第2～4周半峰值比的影响较小，采用空气中常用的标准半峰值比进行周期识别通常不会产生错周现象，但入水深度超过2m时，由于波形形变严重，采用空气中常用的标准半峰值比进行周期识别将会产生错周现象，导致定位结果不可用；在淡水中40m以下深度时，采用空气中常用的标准半峰值比进行周期识别一般不会产生错周现象，但入水深度超过40m时将会产生错周现象。

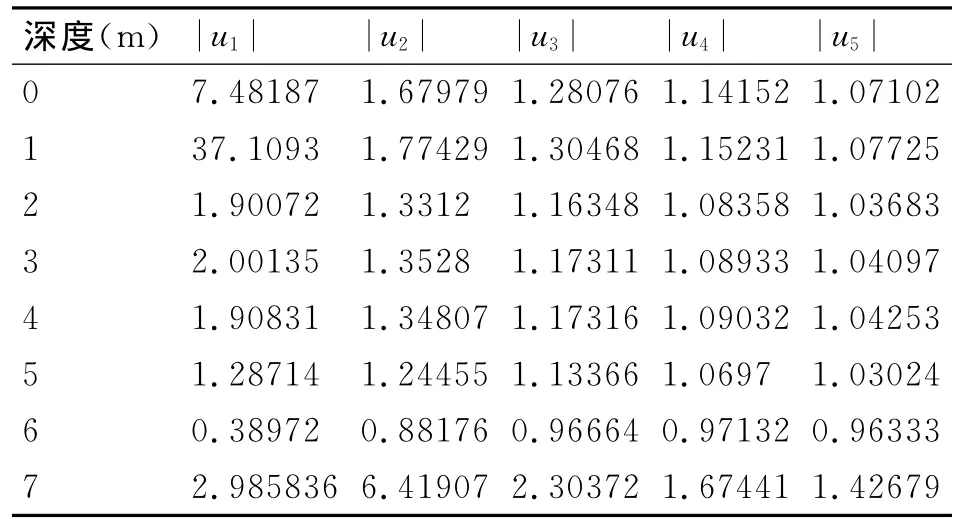
表1 海水中不同深度色散信号半峰值比

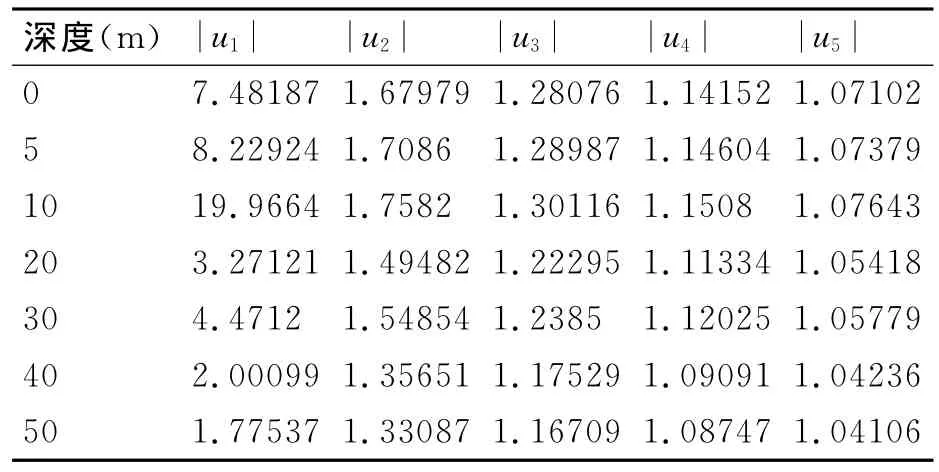
表2 淡水中不同深度色散信号半峰值比

3 水下接收信号包周差补偿方法设计

由上一节分析可知，由于色散效应，罗兰C信号在海水中传播深度超过2m，在淡水中传播深度超过40m时，需要对信号的包周差进行补偿才能准确地实现周期识别，得到正确的定位结果。因此，本文将在结合常用周期识别方法优点基础上，设计一种基于最小均方误差思想的周期识别方法，然后采用表1、表2中对应深度的半峰值比仿真结果进行匹配识别，以补偿色散效应对罗兰C信号产生的波形形变。

常见周期识别方法有幅值比法、画切线法、场强法、一次微分法、延迟倒相法及和函数法等多种方法，其中应用较多的是延迟倒相法与和函数法。此外，近年来国内部分文献中提出了匹配相关的周期识别方法[9～10]。由于和函数法保留了罗兰C信号的波形特征，通过多周期波形累加能够有效提高信号信噪比，提高周期识别的准确性与接收机定位精度；而匹配相关法能够充分利用罗兰C信号包络及载波前三周信号幅值比特征，对提高罗兰C信号周期识别的准确性具有重要意义。因此，本文在设计周期识别方法时，将充分结合上述两种方法的优点，在和函数识别法基础上融入匹配相关算法，并结合水下不同深度的半峰值比仿真结果实现准确的识别，其具体实现步骤如下：

1）由于相位跟踪点位于载波周期前40μs的某一过零点，在跟踪点前以10μs为间隔选取m1个零点，在跟踪点后选取m2个零点；

2）对选取的所有零点都按照和函数法计算选取零点的半峰值比ki（i＝1，2，…，m1＋m2＋1）；

3）以k01，k02，k03表示罗兰C标准信号载波第2～4周半峰值比，则利用匹配算法可计算得到上述半峰值比序列相对标准值的均方误差：

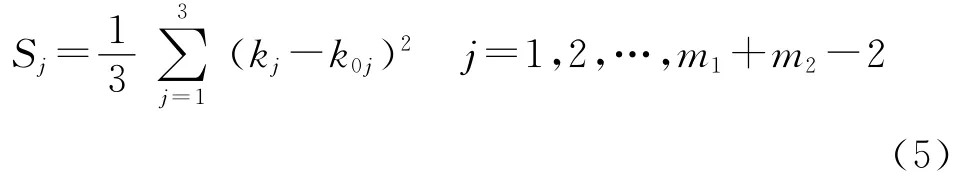
4）对均方误差Sj进行比较，最小的Sj对应的半峰值比kj＋2所对应的零点即为载波第三周末过零点，即实现了信号的周期识别。

在实际运用过程中，用前一节表1、表2中的不同深度下的载波第2至4周半峰值比代替上述算法中的k01、k02与k03，以实现水下接收信号的包周差补偿。

4 试验分析

为验证色散效应对罗兰C信号的影响以及采用包周差补偿的最小均方周期识别方法的正确性与有效性，笔者利用磁性天线进行了大量的水下接收信号采集试验，其中接收到的一组信号如图3所示，相关试验现场如图4所示。从大量采集数据中分别挑选出一组武汉木兰湖的试验数据与一组海南三亚附近海域的试验数据，对两组数据进行自动搜索与相位跟踪之后，在本文所设计基于最小均方思想的周期识别方法中融入第2节不同得到的水深下的半峰值比进行匹配，然后进行定位解算并与对应水域表面的定位结果进行比对分析，其结果如表3所示。

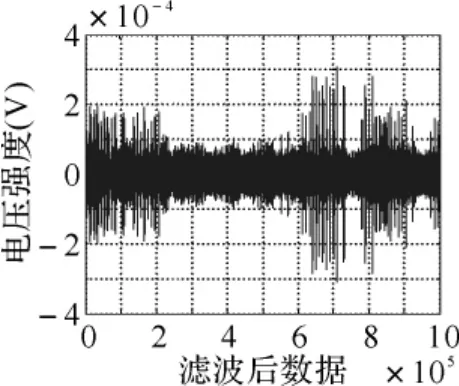
图3 海南三亚附近水域接收到的水下罗兰C信号

图4 木兰湖与三亚附近海域试验

由表3可见，在淡水中10m深处，由于色散的影响较小，罗兰C信号波形形变较小，第2、3、4载波周期的半峰值比改变较小，利用空气中的标准幅值比匹配不影响载波第三周的正确识别，定位精度基本不受影响；但在海水中，由于色散效应较强，对罗兰C信号的波形影响较大，如果不进行包周差补偿，继续使用空气中的标准幅值比进行匹配，则会导致周期识别错误。如表中海水中2m与5m深处，由于测量点距离主台与副台2较近，测量得到的时差TD2较准确，但时差TD1比空气中的测量值小近10μs，即向前跳了一周；同理，在海水中7m深处，测量时差TD1比空气中的测量值大约20μs，向后跳了2周。对上述问题进行包周差补偿，即采用色散后的半峰值比进行重新匹配并进行周期识别，得到的时差如表中ECD补偿后的时差所示，其结果与空气中得到的时差基本一致，定位结果可信。由此可见，色散会导致罗兰C信号的波形发生形变，在海水中如果不进行包周差补偿将会导致定位结果不可用，由此也证明了在本章设计的最小均方周期识别方法基础上融入包周差补偿能够有效解决海水对罗兰C信号传播产生的影响，提高周期识别的准确性与定位精度。

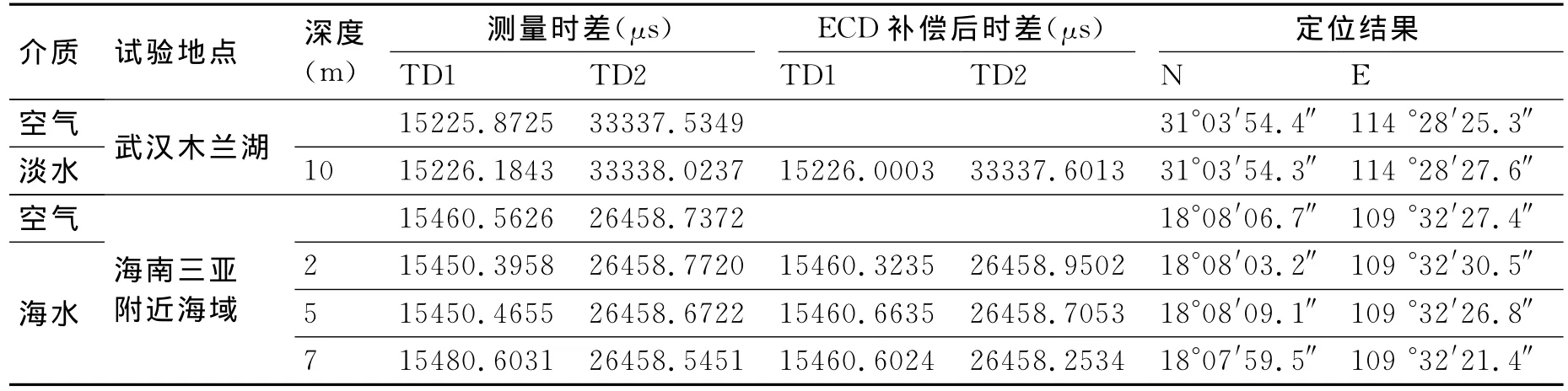
表3 试验结果

5 结语

本文分析了罗兰C信号的水下色散特性，得到了色散效应会导致罗兰C信号波形发生形变，需要进行包周差补偿这一结论，并给出了海水与淡水中不同深度下接收到的罗兰C信号的载波前五周半峰值比仿真结果。在此基础上，设计了一种基于最小均方思想的匹配周期识别算法，并结合所得到的半峰值比仿真结果设计了水下接收罗兰C信号的包周差补偿方法。试验结果表明，所设计水下接收补偿方法能够有效补偿色散效应对水下接收罗兰C信号的影响，提高接收机定位精度，对罗兰C接收机的水下应用具有重要意义。

[1]Mohammed A，Chemnitzer H，Last D.Full performance analysis of IFFT spectral－division technique for skywave identification in Loran－C receivers[C]／／Proc.31stAnnual Convention and Technical Symposium，International Loran Association（ILA31），Washington，DC，2002：1～10

[2]Mohammed A，Last D.IFFT technique for skywave detection in Loran－C receivers[J].Electronic Letters，2001，37（6）：398～400

[3]Mohammed A.Effect of Loran－C signal parameters on skywave delay estimation of IFFT technique[J].Electronic Letters，2003，39（14）：1091～1093

[4]胡东亮，杨迎春，范菊红.基于MUSIC算法的罗兰C接收机天地波自动识别方法研究[J].海军工程大学学报，2006，18（3）：7～9

[5]杨迎春，杨新峰.一种高分辨率的罗兰C接收机天波延迟估计技术[J].计算机仿真，2006，23（7）：295～298

[6]周新力，刘华芹，孟庆萍，等.罗兰C接收机天波识别技术研究[J].现代电子技术，2007（23）：36～44

[7]朱银兵，许江宁，王红星，等.基于IFFT频谱相除的罗兰C天地波识别新算法[J].电子与信息学报，2009，31（5）：1153～1156

[8]朱银兵，许江宁，崔国恒，等.罗兰C周期识别时频分析方法研究[J].电子与信息学报，2010，32（3）：732～736

[9]陈秋月，杨会成，江太辉.基于匹配相关法的罗兰C信号周期识别[J].无线电工程，2007，37（12）：27～29

[10]林慧珍，罗斌凤，胡东亮，等.波形匹配法识别罗兰C信号周期[J].舰船电子工程，2008，28（5）：81～83