基于信息系统的体系作战中对火力“集中”问题的定量分析研究＊

刘晓天 夏有仓 杨丹峰 刘式宋

（71262部队司令部 驻马店 463200）

1 引言

基于信息系统的体系作战，信息已成为武器装备乃至整个军队发挥作战效能的关键。战斗原则“集中火力、重点打击”的内涵将发生重要变化。因此，在原有集中的原则上，我们要充分考虑到“信息”这个因素。同时，“集中”已不单单是“火力”上的集中，而应该是在信息化条件下的信息与兵力、火力的综合集中。如何做到集中，是首先对信息辅助系统集中攻击，还是首先攻击敌火力单位，两者兵力应该如何分配，这些问题都需要进一步的研究。

2 建立模型

建立常规作战下的数学模型，假定：

1）炮兵和目标的现存单位火力都构成一个具有平均发射率为λ的泊松射击流，λ为常数。每一方的每一个火力单位可以向对方任何一个火力单位进行瞄准射击，即射击瞄准敌方某个确定的火力单位。

2）一次成功射击至多击毁一个火力单位，被击毁的火力单位不再参战。

3）发射后可立即获得有关目标被摧毁的情报，如击毁目标，射击火力可瞬时转移至对方另一个火力单位。

4）炮弹飞达目标的时间很短，与战斗的持续时间相比可以忽略。

5）任何一方的火力与火力单位的幸存数与数学期望值成正比。

记我敌双方每次在瞄准对方射击时，击毁目标的概率分别为P1、P2；记我敌双方在时刻t的平均火力单位数，即平均幸存火力单位数分别为x、y。

由假设条件1，双方平均发射率，即单位时间内的平均射击次数，分别为λ1、λ2。

由假设条件4，在t到t＋Δt时间间隔内，敌方y个火力单位将要实施ayΔt次成功射击，a＝λ2P2，故我方火力单位的损耗数为：

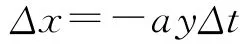
即

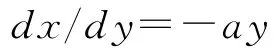
同理

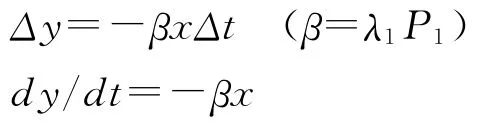
从而得到描述“集中火力”对抗的敌我双方的平均实力变化的微分方程组：

上述模型是在常规条件下建立的。而信息化条件下，敌我双方除了常规部队之外，还有一定的信息辅助系统，与常规武器不同的是，信息辅助系统不是直接对敌进行火力打击，而是通过控制常规武器的火力进而实现其作战效能。所以，无论是我方还是敌方，都将有两个打击目标。一个是对方的作战部队、有生力量，从而降低来自对方作战部队的直接威胁，如敌炮兵、装甲兵、步兵都是这种目标；另一个是对方的信息辅助系统，以消灭对方作战部队的间接作战力量，降低其杀伤效率。因此，交战双方的作战部队都将存在火力分配问题，即先攻击对方哪种作战力量，或以什么样的火力对敌同时进行火力打击。

信息化作战条件下，假设是在有信息辅助系统与炮兵火力系统共同参战，在上述模型的基础上，作以下假设：

1）我方和敌方在作战时，均有相应的信息辅助系统协助作战。

2）信息辅助系统并不直接参战，其作战效能则通过作战部队得以实现。

3）我方的作战单位的实力设为x1，敌方的作战单位的实力设为y1，设我方的获取信息的性能为x2，敌方的获取信息的性能为y2。

4）设作战的有效时间为[0，T]，即到达时间T，有一方可能被完全歼灭。

设敌方对我方信息辅助系统的毁伤系数是a，我方对敌方信息辅助系统的毁伤系数是b，而敌方部队y1对我方部队x1的毁伤系数受敌方信息辅助系统y2的影响，所以我们用函数f（y2）表示。

由于信息辅助系统对提高作战单位作战效果起积极作用，所以，有

同时，信息还存在阈值效应，即随着信息辅助系统性能的提高，它对提高作战单位作战效果的作用将会减少。故又有：

同理，若用g（x2）表示x1对y1的毁伤系数，则函数g（x2）也应满足类似于式（2）、式（3）的条件。

我们可以用图1来表示作战态势。

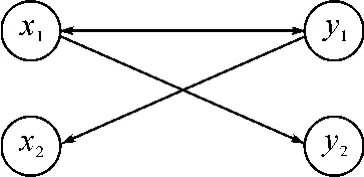
图1 作战态势图

设敌方火力单位（y1）用来攻击我方火力单位（x1）和我方信息辅助系统（x2）的比例分别是φ1＝φ1（t）和φ2＝φ2（t），我方火力单位（x1）用于攻击敌方火力单位（y1）和敌方信息辅助系统（y2）的比例分别为φ＝φ1（t）和φ2＝φ2（t）。则有：

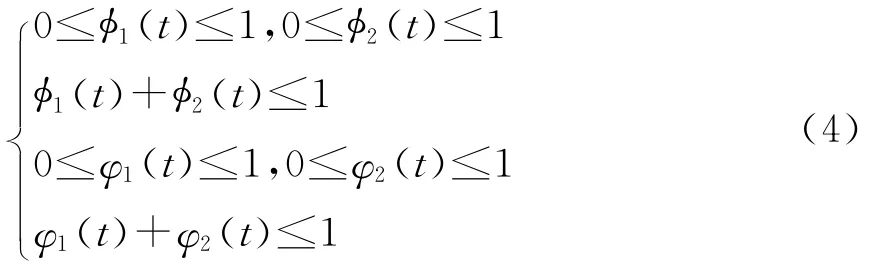
设我方和敌方的初始状态为

在模型（1）基础上，建立模型：

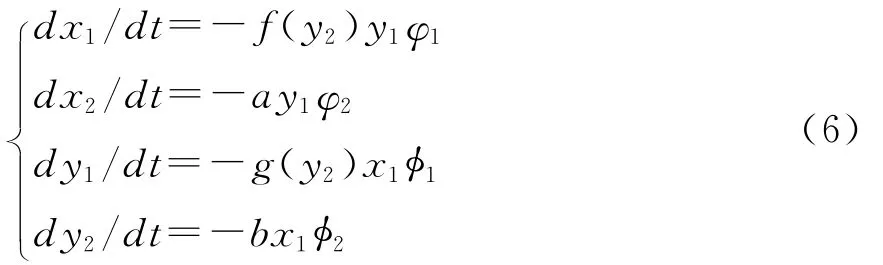
根据假定，在时间t＝T之前，我方和敌方的交战单位都没有被消灭。在此，引进“作战指数”这个概念。所谓作战指数，是指任何一类作战单位的作战效能都可以折合成一定数量的标准作战单位的作战效能，这个数量就称为该类作战单位的“相对作战指数”简称为“作战指数”。在此，我们用u1和v1分别表示我方和敌方的作战指数。有u1＞0，v1＞0。

则双方的实力，即总作战指数可表示为：假定我方获胜，即X－Y＞0。若X－Y＜0，表示敌方获胜，分析方法不变。令

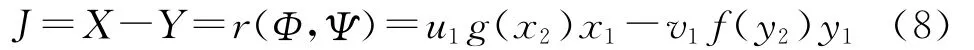
于是，对于我方来说，应力求在T时刻使XY尽可能大，而敌方则力求使X－Y尽可能小。这样，整个作战便可表示为模型式（6）在初值条件式（5）下求满足条件式（4）的最优解问题。

即求Φ＊，Ψ＊，使得

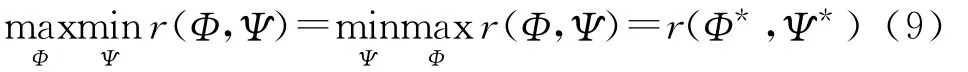
初值已知，则状态轨线x1＝x1（t），x2＝x2（t），y1＝y1（t），y2＝y2（t）就间接由策略Φ，Ψ确定。即选取什么样的策略，作战结果便也会相应改变。同时，交战过程中，x1，x2＞0，y1，y2＞0。

3 模型求解

引入伴随函数λ（t）＝[λ1（t），λ2（t）]T，μ（t）＝[μ1（t），μ2（t）]T，结合式（7），于是 Hamilton函数

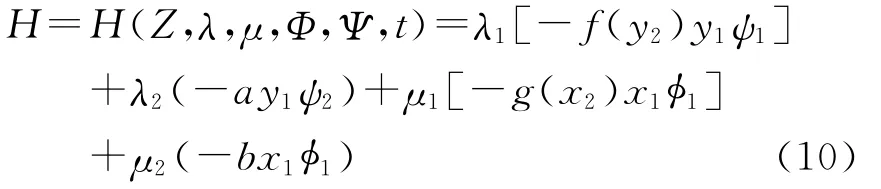
根据微分对策理论，微分对策问题有最优策略

Φ＝Φ＊（t），Ψ＝Ψ＊（t）

及相应的状态轨线

x＝x＊（t），y＝y＊（t）

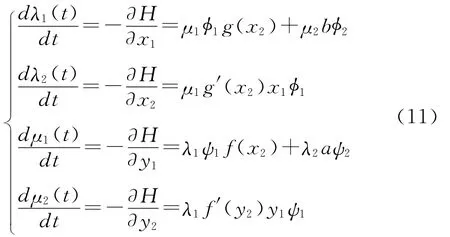
及

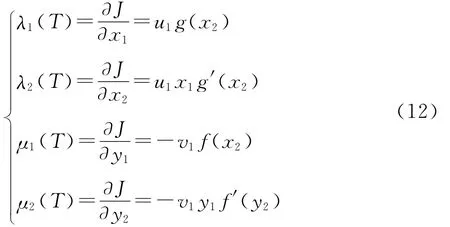
并对于作战时每一时间t∈[0，T]，有

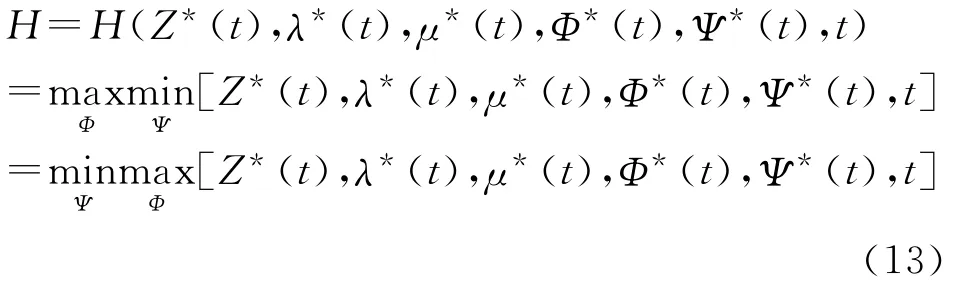
直接求出一组最优解Φ＊，Ψ＊，Z＊，λ＊，μ＊非常困难，在此，我们可以通过逐步分析来寻找求解的关键。

由式（12）易知

对任意时刻t，显然x1（t），x2（t）的增加会导致目标函数J＝X－Y的增加，同时y1（t），y2（t）的增加会导致目标函数J＝X－Y的减少，由伴随函数的定义知

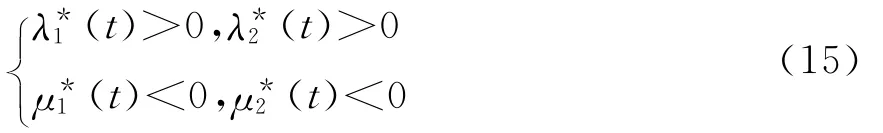
式（10）可以写成

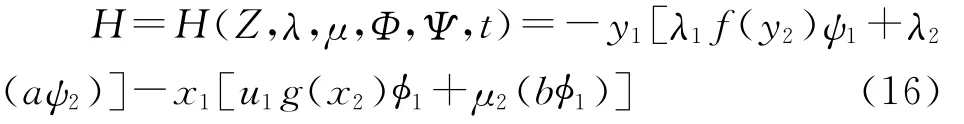
4 分析讨论

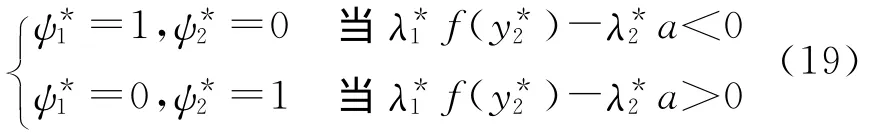
同理，有

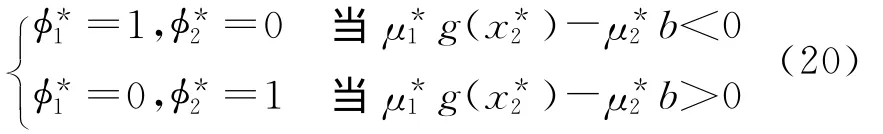
由于λ＊（t），μ＊（t）在[0，T]范围内可以连续变化，同时函数f和g也连续，所以，策略函数Φ＊（t）和Ψ＊（t）在[0，T]上分段取常数。

5 结语

通过模型求解发现，在基于信息系统的体系作战中，火力“集中”的原则仍然适用，但是集中的内容要发生变化，由单纯的兵力或火力集中转变为信息化条件下的综合能力集中，由火炮的简单叠加转向系统的综合集成，并有以下结论：

1）对于信息化条件下炮兵的作战进程，交战双方的最优火力分配是存在的。

2）交战双方需要遵循“集中”的基本战术原则，双方的最优策略就是在每一瞬时，使其作战单位集中力量攻击对方的火力部队或者信息辅助系统。

3）敌我双方的最优火力分配呈现相对稳定性，在一定时间内保持不变。

4）在某一作战时刻首先或者重点攻击敌何种作战单位，应由作战时刻具体态势而定。

[1]姜启源.数学建模[M].北京：高等教育出版社，2003

[2]元书俊，李谋琴.信息化条件下作战的6个特点[J].炮兵学院学报，2009（3）

[3]陈之宁.模糊数学及其军事应用[M].北京：海潮出版社，2006，1

[4]王可定.作战模拟理论与方法[M].长沙：国防科学技术大学出版社，2007，10

[5]卢开澄.单目标、多目标与整数规划[M].北京：清华大学出版社，2009，7

[6]数学实践与认识[C]／／北京：中国数学学会，2004，2

[7]李春立.一体化联合作战指挥[M].北京：军事科学出版社，2004，10

[8]冯良，朱健.现代联合作战[M].北京：军事科学出版社，2008，11

[9]逯兆乾.论21世纪初炮兵作战指挥[M].北京：国防大学出版社，2001，8

[10]丁晓明，徐瑞恩，顾健.高技术战争与作战运筹分析[M].北京：海潮出版社，2006，10

[11][美]斯瓦图，维恩.信息战争[M].长春：北方妇女儿童出版社，2007，10