一种基于Arnold 置乱的FRFT数字图像水印方法

高宁宁，杨文考

（北京交通大学电子信息工程学院，北京100044）

随着网络化、信息化进程的不断加速，对数字产品版权保护的要求也日益迫切。因此，有关数字水印的研究发展迅速，王永杰、常志国均在无损数字水印（也称为可逆水印）方面做了一定的研究，分别提出了具有自恢复和篡改定位能力的可逆数字水印方案及大容量可逆水印算法[1~2]。张峰、穆晓敏等人提出了在FRFT域内Chirp类数字水印盲检测算法[3]，其水印采用二维Chirp信号，算法实现了水印的盲检测。F.Q.YU等人选取二维分数阶傅里叶变换的中频系数作为水印添加区域，以一维chirp信号作为水印，进行了仿真，验证了算法的鲁棒性[4]。华北电力大学张兆祥则提出了一种基于FRFT和纹理特征的数字水印算法，仿真证明了该算法具有很好的不可见性和鲁棒性[5]。

作为信息隐藏领域研究的热点，数字水印技术在数字产品版权保护、认证与篡改举证、秘密通信与特征标记等方面均有重要应用[6]。数字水印技术是将水印信息嵌入到图像、音频、视频等数字载体中，成为可见或不可见的标志。常用的水印嵌入算法是基于空域和变换域，在现代图像处理技术中，通常用到的变换有离散傅里叶变换（DFT）、离散余弦变换（DCT）、离散小波变换（DWT）等。2001年，I.Djurovic等人提出了基于离散分数阶傅里叶变换的数字水印技术[7]。分数阶傅里叶变换（FRFT）在时频平面上具有旋转特性和角度连续性，加之变换角度提供的自由度，使之兼有空域和频域的特性，可将水印分散到载体图像的多个参数中，有利于保证水印的不可见性、保密性和鲁棒性。此外，FRFT的阶次可以作为检测水印的密钥，从而提高水印的安全性。

1 分数阶傅里叶变换（FRFT）

1.1 FRFT定义

一维连续信号s(t)的p阶FRFT定义为：

其中，Kp(t,u)为变换核。

函数f(x)的p阶FRFT的反变换定义如下：

二维连续信号s(x,y)的分数阶傅里叶变换定义为：

其中，px,py分别为横轴和纵轴方向的变换阶数，Kpx,py(x,y,u,v)是二维FRFT的变换核。

1.2 DFRFT

在工程上，必须采用离散形式的分数阶傅里叶变换（DFRFT），DFRFT的计算复杂度与快速傅立叶变换（FFT）具有可比性，若序列有效长度为N，则其计算量为O(Nlog2N)。

二维离散信号f(p,q)的DFRFT及其反变换定义为：

其中，（α,β）为二维DFRFT的阶数，Kα,β(p,q,m,n)=Kα○Kβ是变换核，Kα，Kβ为一维DFRFT的变换核。

利用矩阵的特征值和特征向量来计算DFRFT，这种方法保持了连续FRFT的特征值—特征函数的关系，克服了特征值与特征向量不匹配的缺点。这种计算方法可以得到与连续FRFT相近的输出结果，其计算复杂度为O(N2)。本文采用特征值和特征向量的计算方法。

从运营投入指标来看，机构16、机构15、机构18的运营投入冗余率皆超过了10%，其中机构16冗余率最高，为21.95%，运营投入冗余率最低的为机构1，运营投入冗余率为6.5%。

2 基于FRFT的数字水印嵌入和提取算法

2.1 水印预处理

本文采用灰度图像作为水印信号，具有一定的标记意义。因为直接嵌入该水印信号不利于信息隐藏，从而降低信息安全性，因此本文采用Arnold置乱对水印进行预处理。置乱变换技术通常作为一种加密的手段应用在水印的预处理中，将一幅有意义的图像经置乱变换变成一幅杂乱无章的图像。在不知道置乱算法和密钥的情况下，攻击者无法恢复出水印，从而达到二次加密的目的。

此外，利用Arnold置乱对水印进行预处理，可以降低水印图像受到攻击时信息的损坏或丢失，对提取的水印进行反置乱处理，损坏或丢失会分散到整幅图像中，从而减少对人眼视觉的影响，相应地提高水印的鲁棒性。Arnold置乱还具有周期性，所以可以找到一个相对的最佳置乱次数，并将其作为水印提取时的密钥。

Arnold置乱[9]定义如下：

其中，x,y为原始空间像素点的坐标，x',y'为经过迭代运算置乱后像素点的坐标，N为图像方阵的大小，也称为阶数。利用式（7），经过多次迭代运算可以实现图像和矩阵的置乱变换。

本文对水印的预处理中，选取置乱次数为8，得到的置乱后的水印及恢复的水印仿真结果如图1。

2.2 水印嵌入

图1 水印的Arnold置乱及恢复

本文选择将水印信息嵌入到FRFT后的幅度谱中，为保证水印不可见性和鲁棒性的统一，选择将水印嵌入到DFRFT的中频系数。不选择图像的低频系数和高频系数的原因在于，通常图像的低频系数较大，集中了大部分能量，如果被修改将影响水印的不可感知性，使图像失真明显。而高频系数则容易受到传输过程中一些处理带来的影响，如低通滤波和JPEG压缩。水印嵌入框图如图2。

水印的嵌入步骤如下：

图2 水印嵌入框图

（1）选取大小为32×32的二值水印图像，进行Arnold置乱预处理。

（2）对载体图像I进行2D-DFRFT变换，选取变换阶数为（α,β），得到变换后的系数矩阵F(u,v)，将该系数矩阵分解为幅度部分A(u,v)和相位部分P(u,v)的乘积。

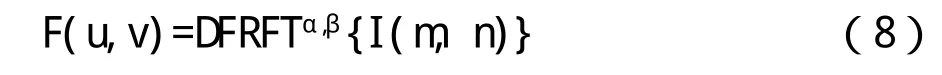
（3）将置乱后的水印降为一维水印序列W'。

（4）选择A(u,v)中间部分的L个较大系数Si作为显著分量，将（3）中的一维水印信息序列叠加在这些显著分量上，得到新的幅度部分A'(u,v)，嵌入方式为：

其中，λ为水印嵌入强度。

（5）将上述新的幅度部分A'(u,v)与原相位部分P(u,v)组合得到新的系数矩阵的矩阵F'(u,v)。最后经过阶数为（－α,－β）的逆分数阶傅里叶变换，得到嵌入水印后的水印图像，即：

2.3 水印提取

水印提取过程即为上述过程的逆过程。首先对水印图像进行阶次为（α,β）的分数

阶傅立叶变换，将系数矩阵分解为幅度部分和相位部分的乘积。对幅度部分的中间L个系数进行判断得到置乱后的水印信息，最后经过Arnold反置乱得到提取出的水印信息。

3 仿真试验及分析

本文采用MATLAB7.0进行仿真，试验中取大小为256×256的灰度图像为原始图像，采用32×32的二值图像作为原始水印，试验中取Arnold置乱次数为8，分数阶傅里叶变换阶数为（0.85，0.5），水印嵌入强度λ为0.15。

3.1 嵌入水印的视觉效果评价

嵌入水印后的图像质量可以由峰值信噪比（PSNR）来评价，一般用PSNR来衡量嵌入水印后的图像的失真程度。

其中，I为原图像灰度值，I'为嵌入水印后的图像灰度值，M为原图像灰度值的最大值。PSNR值越高，原始图像失真程度越小，视觉评价效果越好。

采用本文方法，得到的水印图像峰值信噪比为PSNR=39.21 dB。从图3可以看出，原始图像在嵌入水印后，在视觉效果上基本没有失真，具有良好的保真性和不可见性。

图3 原始水印与嵌入水印后的水印图像

为了对比效果，本文又依次采用了基于LSB变换、DWT变换及DCT变换的方法进行了仿真实验，从仿真结果得知，本文方法不仅在运行时间上具有一定的优势，且在视觉效果上具有更好的保真性。

3.2 抗攻击性分析

为了验证本文算法的鲁棒性，分别对水印图像在JPEG压缩、噪声干扰、滤波、图像剪切等几种典型的攻击下进行了仿真分析。

提取的水印与原水印的失真程度通常用相关系数来度量，归一化的相关系数（NC）定义为：

其中，w为原水印，v为提取的水印，水印的大小为M●N。当NC大于一定值时，则表明可以有效地提取水印信号。

图4与表1的实验结果表明，对嵌入水印的图像进行JPEG压缩、噪声干扰、滤波以及图像剪切等各种攻击，都能有效地提取水印，具有较强的鲁棒性。

图4 原始水印与提取的水印图像

表1 各种攻击下的水印鲁棒性测试

4 结束语

本文将分数阶傅里叶变换与数字水印技术相结合，提出了一种基于Arnold置乱的FRFT域数字图像水印方法。仿真结果表明，水印具有良好的不可见性和鲁棒性，能够很好地抵抗各种常见的图像攻击，如JPEG压缩、图像剪切、噪声和滤波等。同时，对水印的Arnold置乱预处理将有意义的灰度图像水印经置乱变换变成一幅杂乱无章的图像，使得水印信息更好地隐藏起来，提高了信息安全性。

[1] 王永杰. 无损数字水印技术研究[D] . 北京：北京交通大学，2006.

[2] 常志国. 可逆水印与图像保护技术研究[D] . 上海：上海交通大学，2009.

[3] 张峰，穆晓敏，杨守义，齐 林. 基于FRFT盲检测Chirp类数字水印算法[J] . 计算机工程与应用，2006（27）：57-61.

[4] Yh.F.Q,Zhang. Z. K, Xu. M. H. A Digital Watermarking Algorithm for Image Based on Fractional Fourier Transform[J] .Singapore: 2006 IST IEEE Conference On Industrial Electronics and Applications，Vols l-3 2006: 1441-1445.

[5] 张兆祥. 基于分数阶傅里叶变换的数字水印算法研究[D] .北京：华北电力大学，2007。

[6] 章春娥，裘正定. 信息隐藏与数字水印技术[J] . 铁路计算机应用，2001，10（12）:3-6.

[7] I.Djurovic，S.Stankovic，I.Pitas. Digital Watermarking in the Fractional Fourier Transformation Domain[J] . Journal of Network and Computer Applications，2001，24（2）:167-173.

[8] L.B.Almeida. The Fractional Fourier Transform and Timefrequency Representations[J] . IEEE Trans. Signal Processing，1994（11）：3084-3091

[9] Lingling Wu, Jianwei Zhang, Weitao Deng, Dongyan He. Arnold Transformation Algorithm and Anti-Arnold Transformation Algorithm[J] . Information Science and Engineering (ICISE),2009 1st International Conference on Digital Object Identifier，2009 : 1164 - 1167