圆端型墩高速铁路桥梁的弹塑性地震反应分析*

陈令坤 蒋丽忠 王丽萍 罗波夫

(中南大学土木工程学院∥高速铁路建造技术国家工程实验室，湖南长沙410075)

随着高速铁路在全世界特别是近期在中国的迅速发展，地震作用下高速铁路桥梁的动力响应越来越受到研究者的广泛关注.近年来，国内外学者对桥梁的地震反应研究取得了一定的成果.Xia等［1］利用综合模态技术研究了不同剪切波速地震记录激励下车桥系统的动力响应;Yang、林玉森等［2-3］研究了地震作用下车桥系统的动力稳定性;Zhang等［4］通过虚拟激励法以及精细积分技术研究了横向地震作用下车桥系统的动力响应;关于桥墩试验，Kowalsky等［5-6］采用基于位移的设计方法研究了桥墩延性抗震指标;Kunnath等［7］通过12根四分之一比例模型，研究了混凝土桥墩的累计损伤机理延性抗震指标关于地震反应的分析方法;鞠彦忠等［8］通过对铁路桥梁常用截面桥墩的拟静力实验，研究了桥墩的非线性滞回特性，分析了延性比、耗能特性及最大抗力与剪跨比和配箍率等因素之间的关系;丁明波等［9］以重力式桥墩为原型，研究了模型桥墩在周期性反复荷载作用下的非线性抗震性能.关于地震作用下的车桥相互作用动力分析，既有研究大多集中于桥梁的弹性反应和列车行走安全方面，而没有考虑桥墩的弹塑性地震反应;关于桥墩的试验研究多采用拟静力试验模拟水平地震作用，而没有详细考虑类车荷载的影响.对于高速铁路桥梁的抗震分析方法，《新建车速300-350公里客运专线铁路设计暂行规定》［10］中没有明确规定.

文中在既有研究的基础上，基于ANSYS大型有限元分析软件，以高速铁路最常用的多跨简支梁桥为工程背景，建立高速铁路多跨简支梁桥体系的全桥模型，分析结构的自振特性.通过改变地震激励、地震强度、列车速度、墩高等参数，计算列车－桥梁系统的弹性地震反应，并通过赋予非线性梁单元弯矩－曲率关系计算桥墩的弹塑性地震反应，以期为高铁桥梁的抗震设计以及抗震性能评价提供参考.

1 车桥系统有限元模型

既有研究表明，对于多跨简支梁桥，跨数对桥梁、线路结构和机车车辆的振动有着不同程度的影响.就桥梁和列车的振动响应而言，对多跨连续布置的简支梁计算时不应少于4跨，文中取5跨建立计算模型.为考察地震作用下的桥墩的动力响应，采用ANSYS有限元程序及APDL参数化语言建立某高铁多跨简支梁桥的车－桥系统空间分析模型，车辆荷载采用弹簧－质量系统模拟，输入德国低干扰谱高低时域不平顺.采用Beam188单元模拟箱梁和桥墩，支座采用Combin14单元模拟两个水平方向(横桥向和顺桥向)和竖直方向的剪切刚度，墩底固结.多跨简支梁桥的有限元模型见图1，德国低干扰谱轨道高低时域不平顺样本见图2.

图1 5跨简支梁桥有限元模型Fig.1 Finite-element model of five-span simply-supported bridge

图2 德国低干扰谱轨道高低时域不平顺样本Fig.2 Time-domain vertical profile irregularity specimen of German railway with low power spectrum density

2 地震动的选取

GB 50011—2010《建筑抗震设计规范》中规定:采用时程分析法时，应按建筑场地类别和设计地震分组选用不少于两组的实际强震记录和1组人工模拟的加速度时程曲线.GB 50111—2006《铁路工程抗震设计规范》中规定桥梁抗震验算时，应分别计算顺桥向和横桥向的水平地震作用.文中选择3组典型的强震记录，采用Ex+0.65Ex(水平x方向和竖直z方向的地震荷载，竖直z方向的地震荷载取水平x方向的65%)，Ey+0.65Ey(水平y方向和竖直z方向的地震荷载，竖直z方向的地震荷载取水平y方向的65%)组合作为地震激励.对地震动进行比例调幅，将实际地震记录的峰值折算成所需的基本烈度即可使用.强震加速度时程曲线如图3所示.

3 车桥系统地震微分方程的求解

图3 地震加速度时程曲线Fig.3 Acceleration time history curve of earthquake

地震荷载作用下桥梁的振动方程为式中，M、C和K为t时刻列车－桥梁系统的质量矩阵、阻尼矩阵和刚度矩阵，u、u、u为t时刻列车－桥梁系统的加速度、速度和位移列向量，f0为簧上质量(车体)和簧下质量(轮对)形成的广义力分量，fg为地震力分量.桥梁方程建立后采用Newmark-β法求解.

4 车桥系统地震分析算例

4.1 车桥系统基本参数

选取高速铁路5跨简支箱梁桥为研究对象，取第3跨代表整个结构进行地震分析.基本设置如下:次C50混凝土32m跨预应力混凝土箱梁;圆端型实体桥墩;墩高8～24 m;2.3 m×6.0 m圆端型截面;设计水平地震加速度为0.20g;罕遇水平地震加速度为0.38g;Ⅱ类场地;8度设防;选取德国ICE列车活载作为高速铁路运营列车活载，列车编组为2×(动+动+拖 +动 +动 +拖 +动 +动)，车辆具体参数详见文献［11］.

4.2 车桥系统动力特性分析

利用前文建立的全桥空间有限元模型进行车桥系统动力特性分析，表1给出了桥的前10阶自振周期和振型特征.从表1中可以看出，自第5阶以后，相邻周期之间相差最小为0.005s，通过对自振特性分析可知，主梁的横向抗弯刚度相对较大，体现为低阶振型主要为墩梁的弯曲振动.

表1 5跨简支梁桥结构的自振周期和振型特征Table 1 Natural vibration periods and mode shapes of five-span simply-supported bridge

4.3 弹性地震分析

根据GB 50111—2006中三水准抗震设计的要求:在多遇地震作用下，桥墩处于弹性工作阶段，地震后不损坏或者轻微损坏，抗震设计按强度理论进行桥墩、基础强度、偏心及稳定性验算;在设计地震作用下，需验算上、下结构连接构造的强度;在罕遇地震作用下，桥墩处于非弹性工作阶段，对钢筋混凝土桥墩进行延性验算或最大位移分析.文中对高速铁路桥进行弹性和弹塑性地震时程分析，限于篇幅，仅列出了El Centro地震动输入的计算结果.

为了详细分析在地震作用下高度铁路桥梁的动力响应，分析时考虑下列工况:(1)桥梁分别取8、12、16、20、24m墩高进行动力计算;(2)列车编组分别以160、200、250、300、350、400 km/h 等车速过桥，为详细考察地震作用的影响，编制ANSYS-APDL程序让列车编组在地震作用时间内都运行在桥上;(3)根据GB 50111—2006中三水准抗震设计的要求，输入设计地震和罕遇地震加速度进行弹塑性地震反应，常遇地震分析略去;采用横桥向+竖向地震组合Ex+0.65Ex和顺桥向+竖向地震组合Ey+0.65Ey组合作为地震激励.

20m墩高+160 km/h车速+纵向设计地震工况下的梁体位移时程和墩底弯矩时程曲线见图4;20m墩高+350 km/h车速+纵向设计地震工况下的梁体位移时程和墩底弯矩时程曲线见图5;横向设计地震+不同车速/墩高下的墩顶位移见图6;纵向设计地震+不同车速/墩高下的墩顶位移见图7.计算结果表明:不同方向设计地震输入条件下，随着车速的增加，结构动力响应相应增加但并非线性增加，车速对地震响应的影响较小;不同墩高输入下，随着墩高的增加，桥梁地震响应增加明显，车速对结构的地震响应影响很小.

图4 20 m墩高+160 km/h车速+纵向设计地震作用下的梁体位移和墩底弯矩Fig.4 Displacement of grider and moment of pier bottom with 20m pier height at a vehicle speed of 160 km/h under longitudinal design earthquake

图5 20 m墩高+350 km/h车速+纵向设计地震作用下的梁体位移和墩底弯矩Fig.5 Displacement of grider and moment of pier bottom with 20m pier height at a vehicle speed of 350 km/h under longitudinal design earthquake

图6 横向设计地震+不同车速/墩高下的墩顶位移Fig.6 Displacement of pier top at different vehicle speeds/pier heights under lateral design earthquake

4.4 圆端型墩的弹塑性地震分析

根据计算结果，在罕遇地震作用下，结构动力响应已远超规范要求，结构进入弹塑性状态.以20m墩高+350km/h车速+纵向罕遇地震为例，墩底弯矩为1.79×108N·m，超过了屈服弯矩2.48×107N·m.因此需要对结构进行弹塑性分析.

GB 50111—2006中规定，罕遇地震下的桥墩地震作用计算可不计活载影响.为详细考察车桥系统在罕遇地震下的动力反应，文中进行有车/无车两种工况下的桥墩罕遇地震响应分析，横向罕遇地震+350km/h车速+不同墩高下的动力响应见表2.计算结果表明，罕遇地震作用下，对比有车/无车工况，车辆荷载对地震响应的影响较小.

为计算最不利荷载组合作用下的桥墩动力响应，下文采用有车工况计算桥墩罕遇地震响应.

(1)文中使用了UC-Fyber软件对圆端型截面桥墩进行弯矩－曲率关系分析，采用Mander约束混凝土模型和钢筋考虑硬化阶段的双直线型模型，输入截面尺寸、纵筋率、箍筋率、混凝土强度以及ANSYS软件计算的轴力，计算桥墩的屈服转角和屈服弯矩、极限转角和极限弯矩，墩底截面弯矩－曲率的骨架曲线响应计算值见表3.

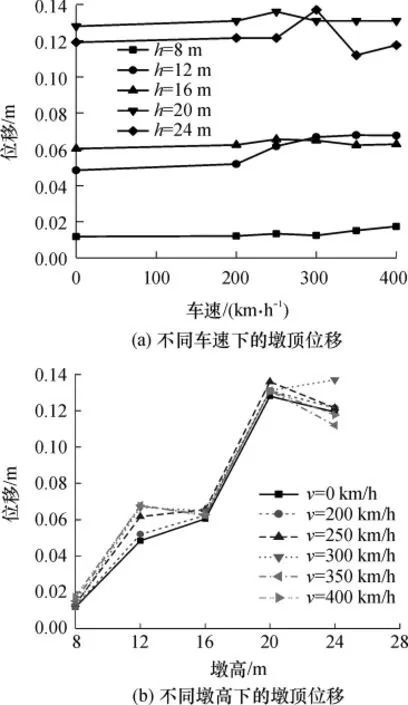
图7 纵向设计地震+不同车速/墩高下的墩顶位移Fig.7 Displacement of pier top at different vehicle speeds/pier heights under longitudinal design earthquake

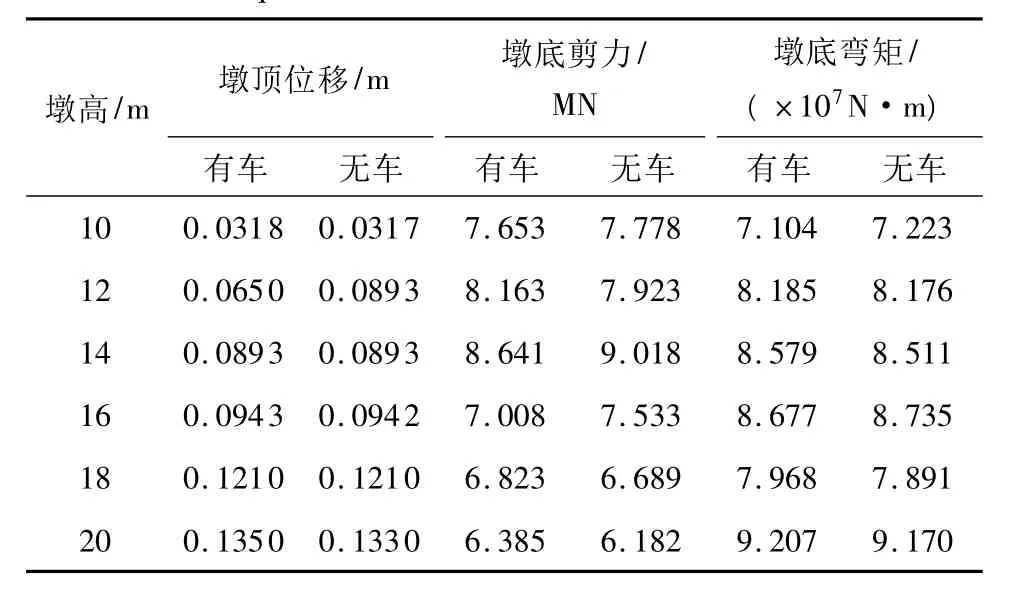
表2 横向罕遇地震+350km/h车速+不同墩高下的动力响应Table 2 Dynamic responses of bridge with different pier heights at a vehicle speed of 350 km/h under transverse rare earthquake

表3 桥墩截面弯矩－曲率的骨架曲线响应计算值Table 3 Calculated values of skeleton-frame curves of momentcurvature relation of piers

(2)将求出的弯矩－曲率曲线赋予非线性墩单元，按照双线性随动强化准则和Mises屈服准则，可以得到墩单元的滞回曲线.

(3)采用Newmark-β法求解非线性地震微分方程时，结构进入弹塑性阶段后结构的刚度将发生改变，需要利用完全Newton-Raphson方法迭代求解位移增量进行非线性地震微分方程求解［12］.

根据弯矩－曲率关系和ANSYS计算结果，以14m墩高+纵向罕遇地震纵向输入为例，200km/h车速时墩底第一个单元的最大弯矩为2.546×107N·m，超出屈服弯矩进入弹塑性阶段，第二个单元的弯矩为2.271×107N·m，小于屈服弯矩;350 km/h车速时墩底第一个单元的最大弯矩为2.515×107N·m，超出屈服弯矩进入弹塑性阶段，第二个单元的弯矩2.272×107N·m，小于屈服弯矩.车速为200 km/h时，墩底第一、第二个单元的弯矩－转角关系见图8;车速为350km/h时，墩底第一、第二个单元弯矩－转角关系见图9.墩单元长度为1.4m，说明距墩底1.4m处截面进入塑性状态;墩底第二个单元未进入弹塑性状态;同时可以看出，墩底第一个单元形成完整滞回环，且回转变形在屈服变形和极限变形之间，说明墩底出现损伤破坏但是尚未达到极限破坏.以14m墩高+350km/h车速+纵向罕遇地震为例，可得强度储备为29.7%;以14m墩高+350km/h车速+横向罕遇地震为例，可得强度储备为12.4%.

图8 14 m墩高+200 km/h车速+纵向罕遇地震作用下墩底第一、第二个单元的弯矩－转角关系Fig.8 Moment-rotating angle relationship at the first and the second elements of pier bottom with 14m pier height at a vehicle speed of 200 km/h under longitudinal severe earthquake

图9 14 m墩高+350 km/h车速+纵向罕遇地震作用下墩底第一、第二个单元的弯矩－转角关系Fig.9 Moment-rotating angle relationship at the first and the second elements of pier bottom with 14m pier height at a vehicle speed of 350 km/h under longitudinal severe earthquake

结果表明，随着车速的增加，墩底弯矩增加不多，塑性铰长度变化不大.参照Eurocode 8规范［13］中的塑性铰长度公式lp=0.08L+0.022dsfy，(L为墩的高度，mm;ds为纵向钢筋直径，mm;fy为纵向钢筋屈服强度，MPa)，以14m墩高+罕遇地震输入为例，塑性铰长度为1296mm，数值分析得到的塑性铰长度为1400mm.Eurocode 8规范塑性铰长度公式是基于Priestley［14］的实验研究得来的，其实验样本设计参数相对圆端型铁路桥墩有所不同，但其实验结果可以作为文中数值分析结果的对比验证.

5 结论

文中运用ANSYS软件和弯矩－曲率分析程序对高速列车桥梁进行弹塑性地震分析，得到以下主要结论:

(1)列车－桥梁系统在设计地震下处于弹性变形阶段，随着车速和墩高的增加，桥梁内力及位移均相应增加，车速的影响较小;

(2)地震强度对结构响应影响较大，罕遇地震作用下墩底进入弹塑性阶段，通过有车/无车工况的计算发现车辆荷载的影响较小，塑性铰位置可以确定并经过验证;以14 m墩高纵向罕遇地震输入为例，距墩底1.4 m处，截面进入塑性状态，建议加密桥墩下部箍筋并加强桥墩与基础的连接.

［1］Xia H，Han Y，Zhang N，et al.Dynamic analysis of vehicle-bridge system subjected to non-uniform seismic excitations［J］.Earthquake Engineering ＆ Structural Dynamics，2006，35(19):1563-1579.

［2］Yang Y B，Wu Y S.Dynamic stability of vehicles moving over bridges shaken by earthquakes［J］.Journal of Sound and Vibration，2002，258(1):65-94.

［3］林玉森.地震作用下高速铁路桥上列车走行性研究［D］.成都:西南交通大学土木工程学院，2007.

［4］Zhang Z C，Lin J H，Zhang Y H，et al.Non-stationary random vibration analysis for vehicle-bridge systems subjected to horizontal earthquakes［J］.Engineering Structures，2010，32(11):3571-3582.

［5］Kowalsky M J.A displacement-based approach for the seismic design of continuous concrete bridges［J］.Earthquake Engineering ＆ Structural Dynamics，2002，31(3):719-747.

［6］Kowalsky M J，Priestley M J N，MacRae G A.Displacement-based design of RC bridge columns in seismic regions［J］.Earthquake Engineering and Structural Dynamics，1995，24(12):1623-1644.

［7］Kunnath S K，Ashraf E B，Taylor A W，et al.Cumulative seismic damage of reinforced concrete bridge piers［R］∥NCEER-97-0006.New York:National Center for Earthquake Engineering Research，State University of New York at Buffalo，1997.

［8］鞠彦忠，阎贵平，刘林.低配筋大比例尺圆端型桥墩抗震性能的试验研究 ［J］.土木工程学报，2003，36(11):66-69.Ju Yan-zhong，Yan Gui-ping，Liu Lin.Experimental study on seismic behaviors of large-scale RC round-ended piers with low reinforcement ratio［J］.China Civil Engineering Journal，2003，36(11):66-69.

［9］丁明波，陈兴冲.客运专线桥梁的抗震性能试验研究［C］∥第十八届全国桥梁学术会议.北京:人民交通出版社，2008:787-792.

［10］中华人民共和国铁道部.新建车速300-350公里客运专线铁路设计暂行规定［S］.北京:中国铁道出版社，2007.

［11］万家.高速列车－无碴轨道－桥梁耦合系统动力学性能仿真研究［D］.北京:铁道科学研究院，2005.

［12］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京:清华大学出版社，2005.

［13］European Committee for Standardization.Design provisions for earthquake resistance of structures，Eurocode 8(Part 2):bridge［S］.Brussels:European Committee for Standardization(CEN)，2004.

［14］Priestley M J N，Park R.Strength and ductility of concrete bridge columns under seismic Loading［J］.ACI Structural Journal，1987，84(1):61-76.