仿鸟扑翼机器人气动力建模与分析*

陈亮 管贻生 张宪民

(1.华南理工大学机械与汽车工程学院，广东广州510640;2.华南理工大学设计学院，广东广州510006)

扑翼飞行是几乎所有自然界具有飞行能力的生物普遍采用的飞行模式，与固定翼飞行相比，这种模式通过翼面的上下扑动同时产生升力和推力，具有效率高、尺寸小和重量轻的优点.自20世纪90年代以来，仿鸟、仿昆虫的微小扑翼飞行器逐渐成为研究的热点，并取得了一些成果［1-3］.但总体而言，对扑翼飞行的研究还处于初始阶段，这主要是由于扑翼飞行模式具有很低的雷诺数(通常小于105)，在这种状态下，气流的粘性力大，升阻比小，对周围气流的微小扰动极其敏感，因此，传统的针对固定翼飞行器的定常空气动力学理论已经不能适用［4］.

针对扑翼飞行的高升力机理，Garrick［5］最早建立了非定常推力模型，Fairgrieve［6］将 Garrick的模型拓展到求解非平面尾流和非正弦振荡的周期运动中，Jones［7］深入分析了非定常尾流的作用，在此基础上，DeLaurier［8］采用叶素理论对大型扑翼机机翼进行了气动力分析.该理论将机翼沿展向分为若干个带状单元，作用于每一个单元上的气动力与该单元的上下扑动和扭转运动相关.Kim等［9］将改进后的叶素理论与流体－结构分析法相结合，分析了扑翼的气动弹性性能，取得了较好的效果.

文中对具有周期性扑动规律的中小尺度仿鸟扑翼机器人进行了运动分析，建立了扑动模型和扭转模型，采用改进的叶素理论对机器人进行了气动力建模，计算结果与实验结果基本吻合.在此基础上，分析了内外翼运动状态和扑动频率对气动性能的影响.

1 运动模型的建立

鸟类翅膀的特殊生理结构以及长期自然进化的结果使鸟类的扑翼飞行具有极其复杂的运动模式，迄今为止人类还无法制造出具有和鸟类相同结构的翅膀，也无法完全模拟出鸟类扑翼的各种飞行姿态.目前的研究主要将鸟类的扑翼运动分解为上下扑动、绕展向轴的扭转和翼面沿展向的折叠，其中翼面的折叠在机构实现上过于复杂，所以目前的扑翼机器人大都没有加以考虑.

文中研究的仿鸟扑翼机器人的基本模型如图1所示.翼面采用低速飞行条件下气动性能较好的半椭圆翼型，前缘为刚性杆，在驱动机构的带动下做周期性上下扑动，翼面材料为聚酯薄膜，具有一定的弹性变形能力，安装时与机身轴线保持一定角度.机翼后缘靠近机身处沿展向进行短距离固定，以减小后缘根部的扑动幅度，使前后缘之间产生扑动相位差，从而形成扭转变形.

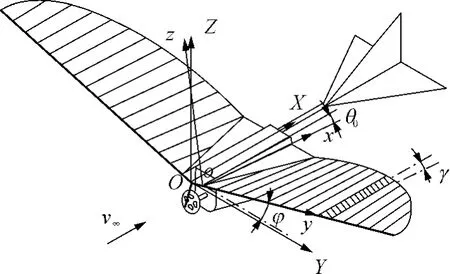
图1 仿鸟扑翼机器人的基本模型Fig.1 Basic model for biomimetic flapping-wing robot

针对以上模型，建立扑动角φ和扭转角γ随时间t变化的运动方程:

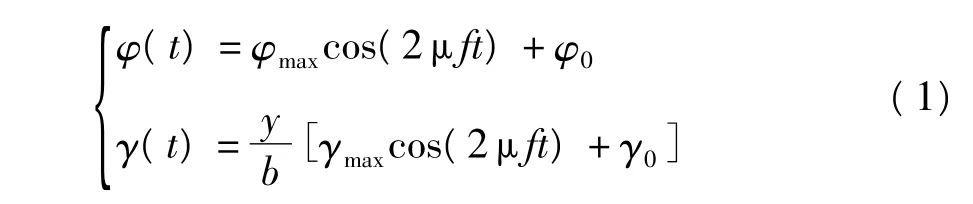
式中，φmax和γmax分别为最大扑动角和最大扭转角，φ0和γ0分别为扑动中间位置处的初始扑动角和扭转角，f为扑动频率，y为翼面展向位置，b为单个翼面的展长.扭转角的变化规律表明，在某一固定时刻，扭转角沿展向线性增大，翼尖处达到最大，这种变化与鸟在实际飞行中的翼面扭转变形一致.

根据叶素理论，沿展向取一微小条带，若扑翼机器人以速度v∞做水平前飞，则该条带具有水平前飞速度v∞、扑动速度vφ和扭转速度vγ.假设机翼相对静止，气流相对机翼运动，取翼型的气动中心即1/4弦线位置为参考点，则翼型的运动模型如图2所示.扑动速度vφ和扭转速度vγ可由下式给出:

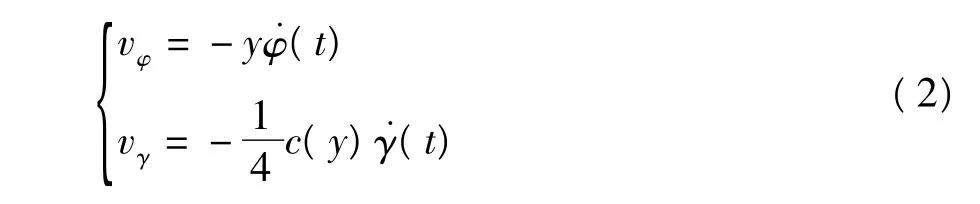
式中，c为展向条带弦长，由翼型形状确定.

根据Rayner［10］对动物飞行非定常空气动力学机理的分析，扑翼飞行时气流具有沿翼面展向的流动，因此需要考虑非定常尾涡对气流的下洗效应.但传统的叶素理论并没有考虑这种下洗效应，因此需要对其进行改进.根据Kuethe等［11］对椭圆翼下洗速度的分析，条带附近气流受到的下洗速度为

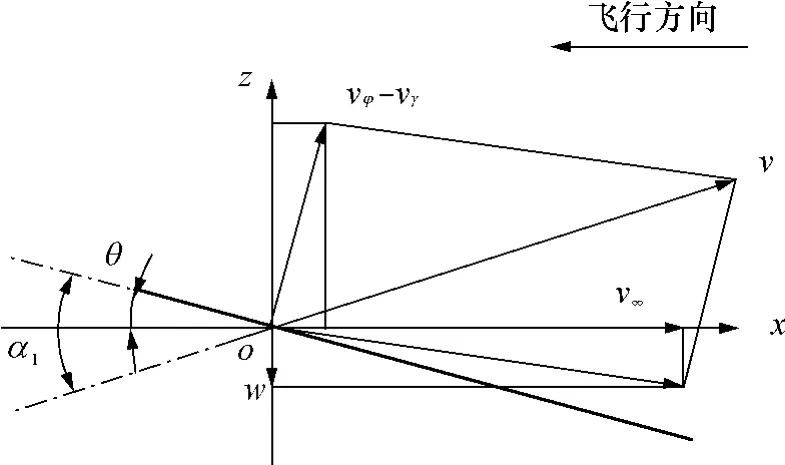
图2 条带的运动模型Fig.2 Kinematic model of wing strip

式中:α0为翼型的零升力迎角，对平板翼型取0;λ为展弦比;θ为静态几何迎角，等于翼型安装角θ0和扭转角γ之和.

根据式(2)和(3)，可以得到气流在条带气动中心处的相对合成速度

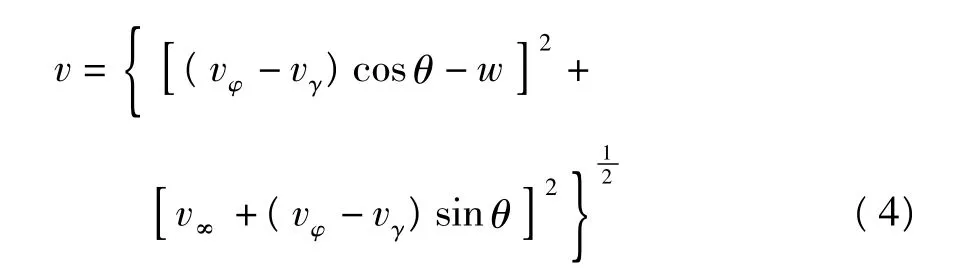
由扑动速度和扭转速度合成而形成的动态迎角为

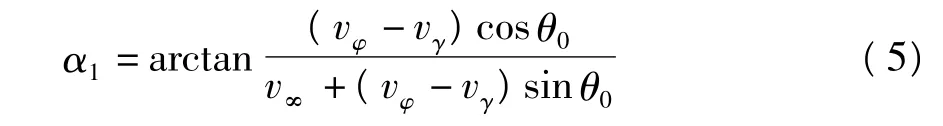
根据Jones［7］给出的非定常法向力系数法对α1进行修正，得到

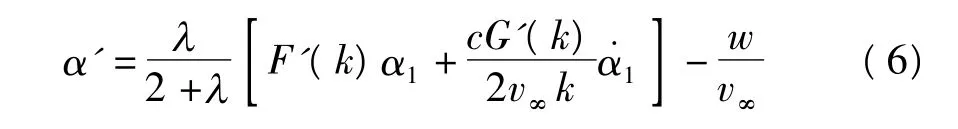
式中，k为减缩频率，反映扑动频率和飞行速度的关系，计算公式为

式(6)中的其它参数根据文献［7］确定.

最后，得到该条带的总迎角

2 气动模型的建立

在水平前飞过程中，沿展向的微小条带受到的气动力主要有:儒可夫斯基升力dNc，附加质量力dNa和摩擦阻力dDf，如图3所示.由于文中所研究的仿鸟扑翼机器人采用平板柔性翼面，因此不必考虑前缘吸力的影响.

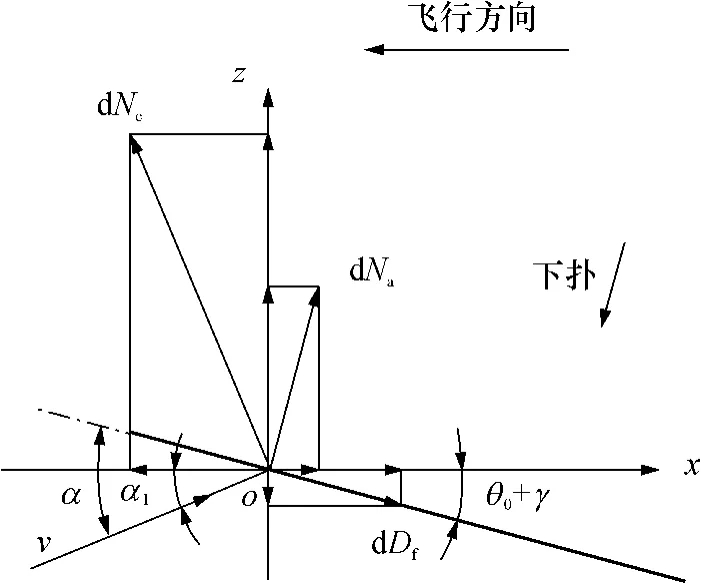
图3 条带的气动力模型Fig.3 Aerodynamic model of wing strip

儒可夫斯基升力由绕翼面的环量产生，是扑翼飞行中的主要升力和推力来源，其方向与合成后的相对来流速度v方向垂直，大小可由下式确定:

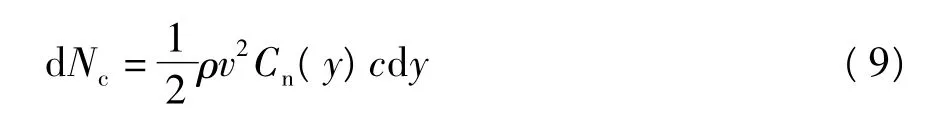
式中:ρ为空气密度;Cn为升力系数，根据薄翼型理论可确定为Cn(y)=2μα.

附加质量力由气流与翼面的相对运动产生，可以表述为由包围条带的虚拟圆柱体内的空气在扑动时作用于翼面上的力［12］，其计算公式为

式中，vN为条带中点处的法向速度，vN=vφ+v∞sinθ－2vγ.

气流对条带的摩擦阻力在翼面切向产生，可由下式确定:

式中:vt为条带中点处的切向速度，vt=v∞cosθ+wsinθ;CDf为平板在空气中运动时的摩擦阻力系数，CDf=1.328/为扑动过程中的雷诺数，Re=为翼面的平均弦长;ν为空气的运动黏度.

将dNc、dNa和dDf向垂直和水平方向分解，可分别得到仿鸟扑翼机器人在飞行中的升力dFL、推力dFT和侧向力dFY:

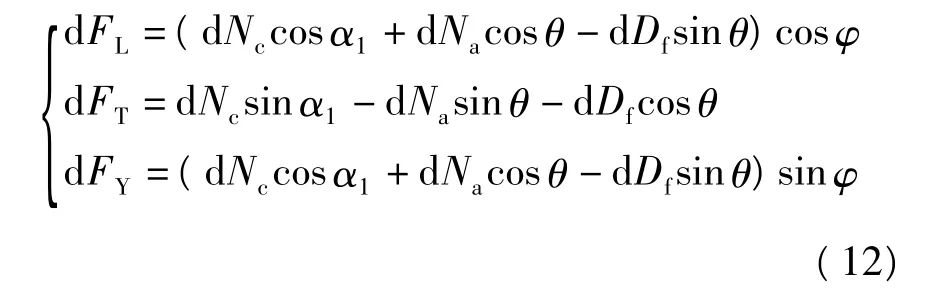
其中，侧向力dFY提供机器人转向时的向心力，若机器人水平前飞，则由于两侧扑翼对称扑动，侧向力相互抵消.本文只针对水平前飞状态进行研究.

将条带受到的升力和推力沿展向积分，并考虑左右两个翼面，可以得到瞬时机器人的总升力FL(t)和总推力FT(t):

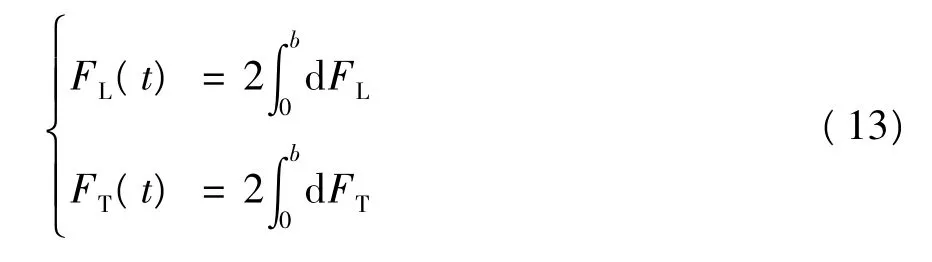
通过在扑动周期T内进行积分并取平均值，可以进一步求得平均升力和平均推力:

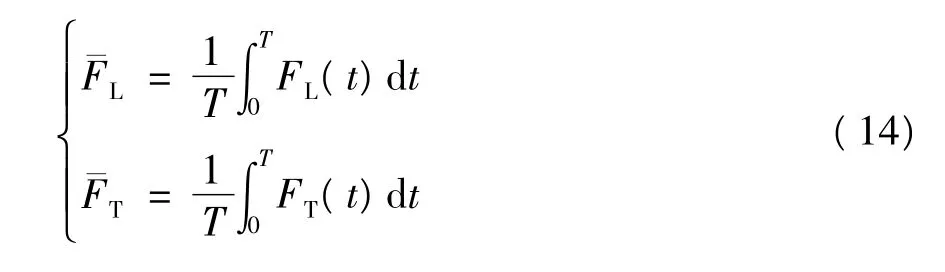
3 实验与仿真结果分析

实验中采用的仿鸟扑翼机器人总质量为16 g，单个翼面展长b为14 cm，翼面安装角θ0为15°，最大扑动角φmax为30°，翼尖最大扭转角γmax为 5°.实验采用ATI-MINI45型六维力/力矩传感器进行气动力测量，采用NI-PCI6224数据采集卡进行实时数据采集，图4为实验中的仿鸟扑翼机器人.

图4 实验中的仿鸟扑翼机器人Fig.4 Biomimetic flapping-wing robot in experiment

在扑动频率f=14Hz、相对风速v∞=2m/s的条件下测得的气动力实验数据与仿真结果如图5所示.图中水平坐标为扑动时间t与扑动周期T之比.

从图5中可以看出:

(1)实验数据与仿真结果总体趋势基本一致，从而证明了该方法的有效性.实验和仿真得到的平均升力分别为0.215N(21.9g)和0.267N(27.2g)，完全可以平衡机器人的重量;平均推力分别为0.095N(9.7g)和0.132N(13.5g)，完全可以提供机器人前飞的动力.

(2)在下扑过程中(0＜t/T＜0.5)，扑翼产生了较大的升力和推力.这是由于在下扑过程中相对气流速度v和相对迎角α都很大，从而使气动力大幅增加.

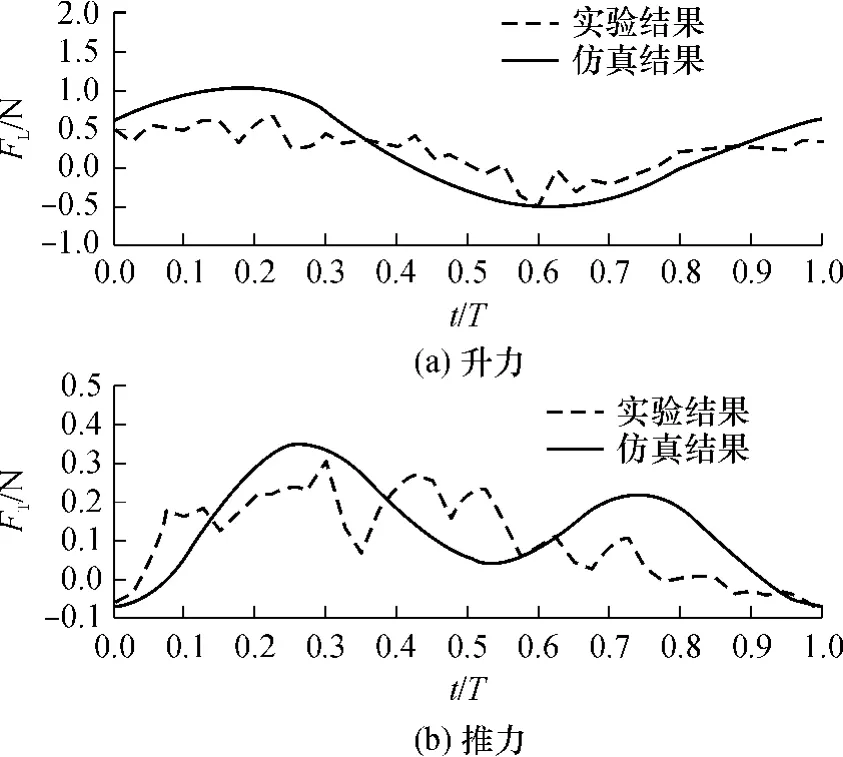
图5 机器人的升力和推力的仿真与实验结果Fig.5 Experimental and simulated results of lift and thrust forces of robot

(3)在上扑过程中(0.5＜t/T＜1.0)，升力转为负值，并逐渐达到最大负升力值，而后再次转为正值;推力先保持正值并逐渐增大，达到最大值后逐渐减小，在上扑结束时转为负值.

上扑过程中气动力产生复杂变化的原因是:在上扑的开始阶段，相对气流速度v较小，相对迎角α仍然保持正值，儒可夫斯基升力与下扑时一样作用于翼面的上方，但值非常小，如图6(a)所示.此时附加质量力占主导地位，使升力和推力迅速减小;随着扑动速度的增加，相对气流速度v也急剧增大，并且作用于翼面上方，相对迎角α变为负值，此时儒可夫斯基升力作用于翼面下方，如图6(b)所示，因此升力为负值，而推力仍然保持正值;上扑结束阶段与上扑开始阶段的升力产生机理相同，只是趋势相反，而推力减为负值主要是由儒可夫斯基升力产生的诱导阻力和附加质量力叠加的结果.

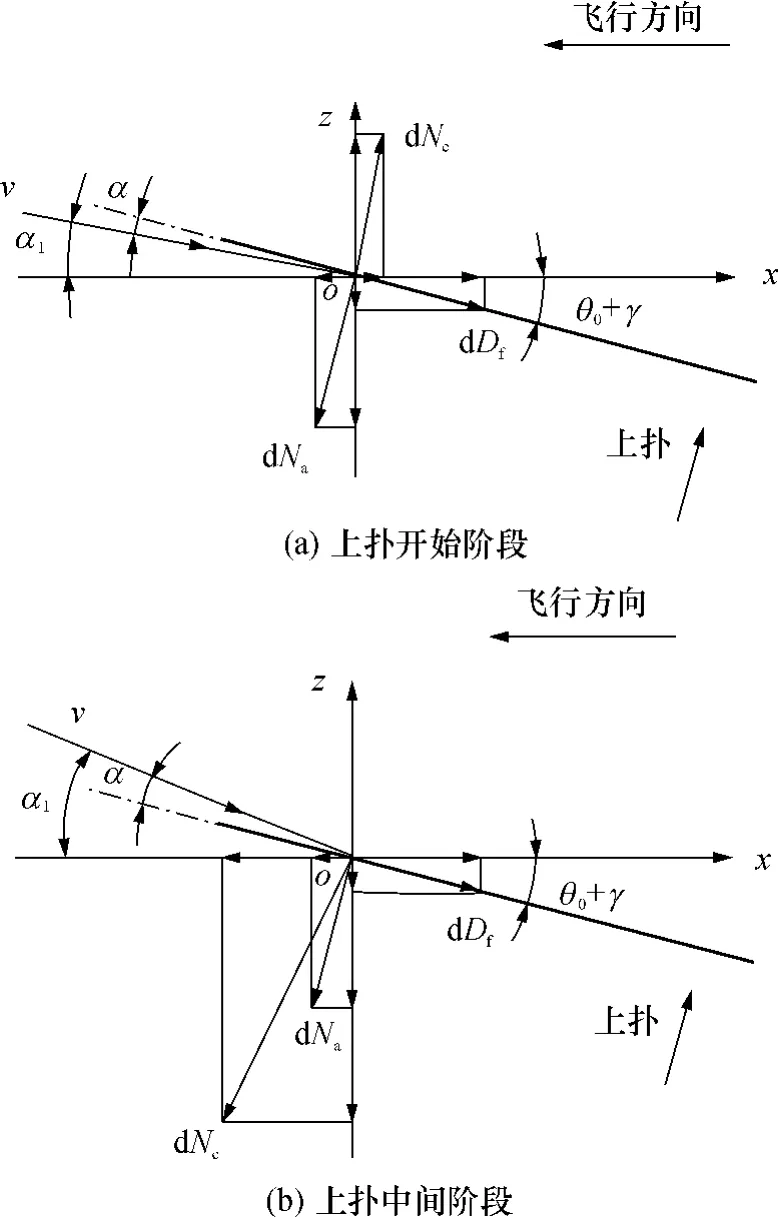
图6 上扑过程中的气动力分析Fig.6 Analysis of aerodynamic forces during upstroke

4 气动特性分析

4.1 内外翼效应分析

由于扑动速度从翼根到翼尖逐渐增大，从而使翼面沿展向的不同位置都具有不同的相对气流速度和迎角，因此内外翼对升力和推力的贡献也有所不同.文中将仿鸟扑翼机器人的翼面沿展向中点位置划分为内翼段和外翼段，分别进行了气动力计算.图7给出了内、外翼段的升力和推力特性曲线.

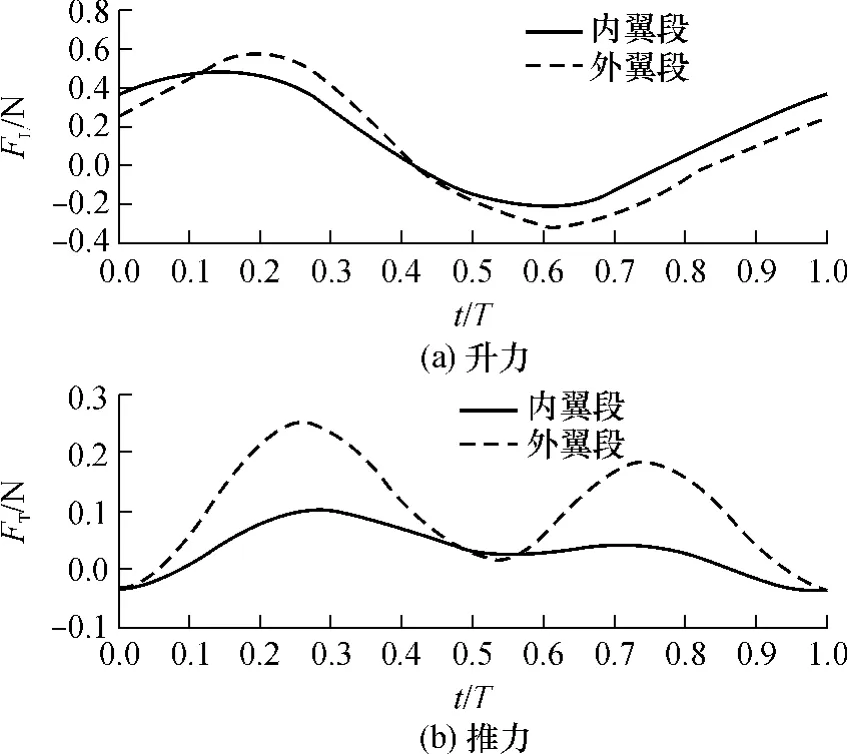
图7 内、外翼段的升力和推力特性曲线Fig.7 Characteristic curves of lift and thrust forces generated by both the inner wing and the outer wing

从图7中可以看出:

(1)对升力而言，内外翼在整个扑动周期中具有基本相同的变化趋势和幅值.经计算，内外翼段提供的平均升力分别占总平均升力的57.4%和42.6%，因此内外翼对升力的贡献基本相当.但仅就上扑阶段而言，外翼对升力的作用要小于内翼.

(2)对于推力，外翼比内翼具有更大的幅值，并且变化趋势更复杂.内外翼段提供的平均推力分别占总平均推力的23.0%和77.0%.因此，外翼在飞行中对推力的贡献要明显大于内翼.

以上结论与对鸟类在飞行中气动力变化观察的结果基本一致.作用于鸟翅膀内外翼的气动力变化如图8 所示［13］.

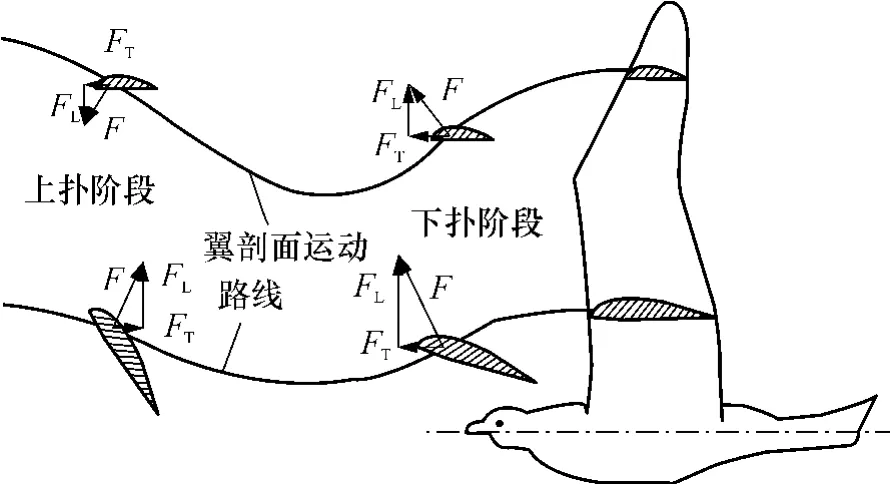
图8 作用在鸟内外翼上的气动力［13］Fig.8 Aerodynamic forces on wing section of a bird

下扑阶段，内外翼均形成正的相对迎角，在翼面上形成正的升力和推力.上扑阶段，内翼的相对迎角变小，产生正的升力和负的推力.与内翼具有的正迎角不同，外翼此时具有较大的负迎角，气动力的合力作用于翼面下方，所以具有正的推力和负的升力.由此可见，翼面沿翼展方向对升力的贡献逐渐减弱，尤其是上扑阶段，靠近翼尖的翼面甚至产生负升力，但在整个扑动周期中，外翼始终对推力有较大的贡献.这种规律可以用来解释鸟类中的一个普遍现象:需要在空中做长时间飞行的鸟(如秃鹫、信天翁等)往往具有比较大的内翼，需要在空中做快速机动飞行的鸟(如鸽子、燕子等)往往具有更加灵活的外翼.

4.2 扑动频率对气动力的影响

以文中提出的模型为基础，通过改变扑翼频率，计算获得了不同频率下的平均升力和平均推力的变化曲线，如图9所示.

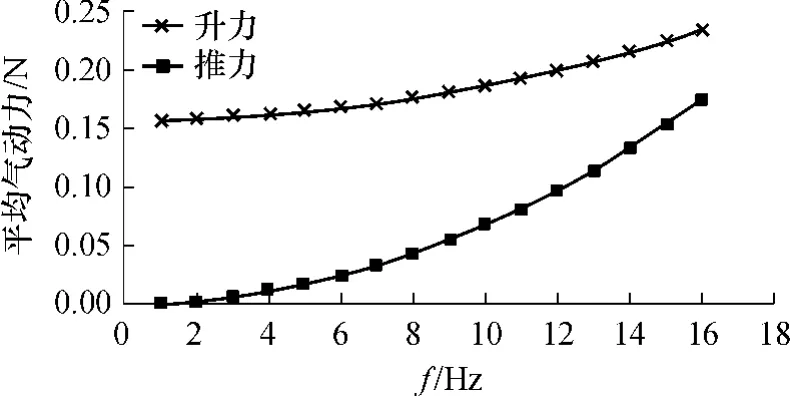
图9 不同频率下的平均升力和推力Fig.9 Average lift and thrust forces at different frequencies

从图9中可看出，频率的增加对平均升力的影响较小，而对平均推力的影响较大.这说明通过增加扑动频率更容易获得大的推力.通过对鸟类的实际飞行状态进行观察发现，鸟类在加快扑动频率时，向前飞行距离的增加量要大于上升高度的增加量.事实上，鸟类在起飞后，一旦升力和重力达到了平衡，飞行速度便成为首要问题，而扑动频率对推力贡献较大的特点也正符合节省能量、提高飞行效率的原则.

5 结论

如何全面模拟鸟类或昆虫的扑翼飞行模式一直是仿生扑翼机器人研制的难点，也是低速非定常空气动力学亟需解决的一个问题.文中以改进的叶素理论为基础，建立了完整的运动模型和气动模型，实验结果和仿真结果总体上保持一致.结果表明:与鸟类的实际飞行情况类似，仿鸟扑翼机器人的下扑阶段是升力和推力产生的主要阶段，上扑阶段会产生负的升力，但推力仍然基本保持正值;内外翼对升力的贡献基本相同，内翼的略大，而外翼对推力的产生具有决定作用;另外，扑动频率的改变对推力的影响大于升力.尽管不同种类的飞行生物所采用的扑翼飞行模式略有不同，但在仿鸟扑翼机器人的研制中，本研究方法是有效的.

［1］Ratti J，Vachtsevanos G.A biologically-inspired micro aerial vehicle［J］.Journal of Intelligent and Robotic Systems，2010，60(1):153-178.

［2］De Croon G，De Clercq K M E，Ruijsink R，et al.Design，aerodynamics，and vision-based control of the DelFly［J］.International Journal of Micro Air Vehicles，2009，1(2):71-97.

［3］Fenelon M A A.Biomimetic flapping wing aerial vehicle［C］∥International Conference on Robotics and Biomimetics.Bangkok:IEEE Computer Society，2009:1053-1058.

［4］Mueller T J，DeLaurier J D.Aerodynamics of small vehicles［J］.Annual Review of Fluid Mechanics，2003，35(1):89-111.

［5］Garrick I E.Propulsion of a flapping and oscillation aerofoil:NACA Report 567［R］.Washington:NACA，1936:419-427.

［6］Fairgrieve J D.Propulsive performance of two-dimensional thin airfoils undergoing large-amplitude pitch and plunge oscillations［D］.Toronto:Institute for Aerospace Studies，University of Toronto，1982.

［7］Jones R T.The unsteady lift of a wing of finite aspect ratio:NACA Report 681 ［R］.Washington:NACA，1940:31-38.

［8］DeLaurier J D.An aerodynamic model for flapping-wing flight［J］.Aeronautical Journal，1993，97(964):125-130.

［9］Kim D K，Lee J S，Lee J Y，et al.An aeroelastic analysis of a flexible flapping wing using modified strip theory［C］∥Proceedings of SPIE:the International Society for Optical Engineering 6928.San Diego:SPIE，2008:1-8.

［10］Rayner J M V.A vortex theory of animal flight(Part 2):the forward flight of birds［J］.Journal of Fluid Mechanics，2006，91(4):731-763.

［11］Kuethe A M，Chow C Y.Foundations of aerodynamics［M］.4th ed.New York:John Wildy，1986:145-164.

［12］Shyy W，Berg M，Ljungqvist D.Flapping and flexible wings for biological and micro air vehicles［J］.Progress in Aerospace Sciences，1999，35(5):455-505.

［13］吴子牛.空气动力学(上册)［M］.北京:清华大学出版社，2007:79-82.