双层公路特大桥的模态参数识别及成桥模型分析*

王荣辉 蔡禄荣 黄永辉 陈孔亮

(1.华南理工大学土木与交通学院，广东广州510640;2.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640)

刚性悬索加劲钢桁梁桥是一种新型的桥梁形式，它结合了传统柔性悬索桥、自锚式悬索桥和连续钢桁梁桥的部分优点，其外形与悬索桥类似，但其采用刚性悬索和刚性吊杆，节点连接也都为刚性连接，在中等跨径桥梁领域具有广阔的应用前景.这种新型桥梁结构受力复杂，在整体上同时具有变高度钢桁梁桥与自锚式悬索桥的受力特点;在局部上，刚性悬索加劲弦杆及刚性吊杆与桁梁的连接与传统悬索桥又截然不同［1］.由于该新型复杂结构在国内首次应用于公路桥梁，因此其整体协同工作性能、动态特性和成桥所采用的有限元计算分析模型的可靠性等有待成桥试验来验证.

模态试验能够识别出系统结构的模态参数(主要为自振频率、振型和阻尼)，其对验证桥梁设计、建立桥梁结构基准有限元模型以及营运状态的健康监测、安全评估具有重要意义［2-4］，因此模态识别及其应用已成为近年来的研究热点.李爱群等［5］采用峰值法在环境激励下对润扬大桥斜拉桥的实测加速度响应进行了模态参数识别，识别了润扬大桥斜拉桥的主要模态频率;任伟新［6］讨论与比较了频域识别的峰值法(PP)和时域识别的随机子空间法(SSI)，建议在自然环境振动条件下将两者结合，以进一步保证结果的准确性;Lardies、Wu和Yang等［7-9］基于实测模态参数对有限元计算分析模型进行了修正.

传统的模态参数识别方法采用人工激振，同时利用激励信号和响应信号进行参数识别.然而，对于大型复杂结构，其质量和刚度都较大，难以采用人工激振.文中直接基于自然环境激振，选择在自然输入更接近白噪声的某晴天的后半夜进行模态试验，然后采用频域法的自谱、互谱和加窗等相关数据处理技术识别模态参数，最后把三维有限元理论计算结果与试验结果进行对比分析，修正理论计算模型.

1 激励响应函数

采用环境激励法不能够了解系统结构的传递函数，只能依靠系统的响应进行模态参数识别.对整个桥梁系统而言，其竖向和横向相当于一根变截面梁.把整体连续结构离散成N个有限自由度系统，根据达朗贝尔原理，可得具有比例阻尼系统的一般性振动方程:

为了方便固有频率的识别，将式(1)转换到频域进行分析.对式(1)进行傅里叶变换，得

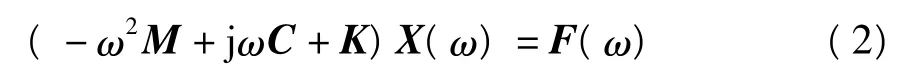
式中:ω为角频率，j为虚数单位，X(ω)、F(ω)分别为x和f(t)的傅里叶变换函数.令

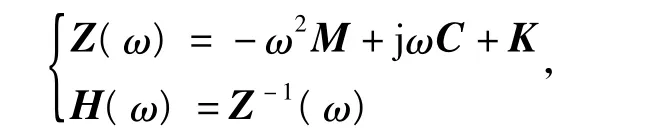
则有

式中，H(ω)为频率响应函数.自然环境激励相当于一个随机信号输入系统，在外界影响因素(风、温度和地脉动等)稳定的情况下，此随机信号接近白噪声，通常可认为其功率谱密度为一常数，即

式中，B为常数矩阵.

令无阻尼自由振动的模态振型为φ，可把x看作是该振型的线性叠加，即

式中，n为模态阶数，qr为模态坐标，φr为M¨x+Kx=0所确定的第r阶模态振型.由各振型之间的正交性，把式(5)代入式(1)后，可推得响应函数X(ω)为

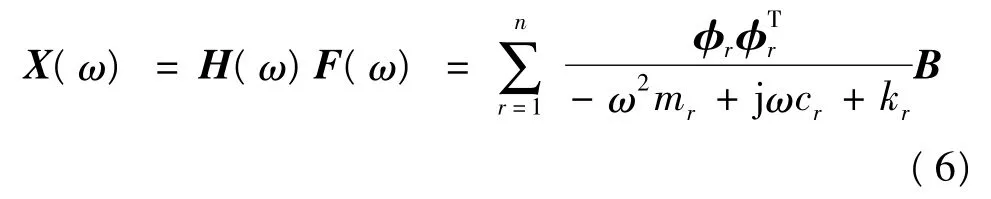
式中，mr、cr、kr分别为系统中的第r阶模态质量、模态阻尼和模态刚度.

式(6)即为用模态叠加法表示的输出响应函数，主要与系统的物理参数有关.

2 模态参数识别原理

结合频域识别的峰值法和互谱分析，可以有效地识别出仅由环境激励的系统结构模态参数.由激励和响应之间的关系式(6)，可得频率响应函数为

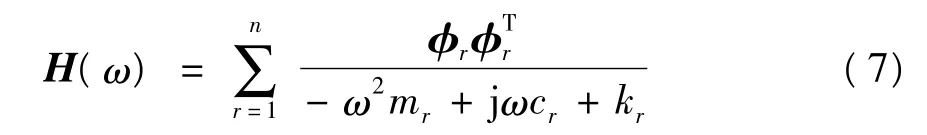
从而由任意节点s激励引起节点i响应的频率响应函数Hi，s(ω)为

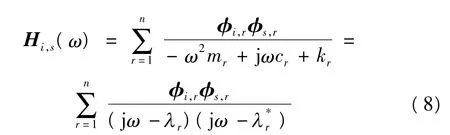
式中，s为结构节点号，s=1，2，…，m，m为结构离散后的节点数，φi，r和 φs，r分别为在任意节点i和节点s处的第r阶振型矢量;λr和为方程 －ω2mr+jωcr+kr=0的一对共轭解.结合式(6)和(8)不难得知，在输入为常数时，响应函数峰值处的频率即为固有频率，在频率响应函数中包含了所有模态信息.

在结构的响应可测，而激励输入不可测的情况下，可假想结构上某一参考节点的响应为输入激励，其他测点的响应与此节点的响应有某种线性相关性，从而建立起响应节点与参考节点之间的传递函数来进行系统参数识别.假定给结构施加的激励力信号为平直谱信号，其功率谱密度函数在覆盖结构全部模态频率范围内为近似均匀分布，即Fs(ω)=d(d为常数).在结构上取一固定参考节点P，则任意节点i的响应Xi(ω)与节点P的响应XP(ω)的比值为

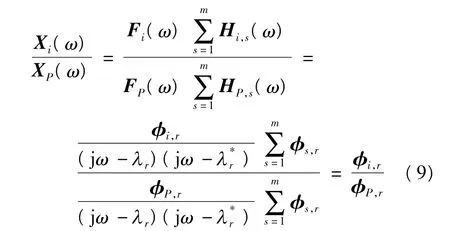
式中:节点P作为参考节点是固定不动的，所以对于一个确定的固有频率是个定值，式(9)即为固定节点P与移动节点i的模态响应传递系数，令其为αi(ω)，即αi(ω)= φi，r/φP，r，从而通过读取测试曲线αi(ω)在ωr处的值(幅值和相位)就可得到固有频率为ωr时的工作曲线，依此可得到结构的第r阶振型.

移动节点i和固定节点P响应信号的互功率谱Gi，P(ω) 为

式中“*”为共轭符号.互功率谱的幅值大小是两个响应信号中各个频率上联合功率的量度，而相位则是联合功率在各频率上的相对出现时间.移动节点i和固定节点P的相干函数为

式中，Gi，i、GP，P分别为节点i和节点P的自功率谱.相干函数反映了两个信号进行互功率谱计算中外来不相干的噪声影响的大小，其区间为［0，1］，相干越大则表示外来影响越小.

大型复杂系统结构的阻尼比一般采用半功率带宽法来识别，此方法是利用自功率谱的共振峰值寻找系统的固有频率，再根据功率谱曲线求得系统阻尼.在纵坐标上寻找半功率点，即取峰值(令对应频率为ωr)的并过此值作一条水平线，它与功率谱曲线的交点称为半功率点，假设两个半功率点对应的频率分别为ωa和ωb(ωa＜ωb)，则求得系统该阶模态阻尼比ζ为

此方法简单易用，在工程中应用极广，但是在小阻尼的情况下，即使低频段的峰值频率存在很小的误差也会给阻尼计算带来较大误差［10］.

3 数值模型与模态试验

3.1 试验桥梁概述

东莞东江大桥是一座三桁刚性悬索钢桁梁双层公路特大桥，在该类桥型中是国内首座.东江大桥主桥全长432m，上部结构为三跨连续钢桁梁，跨度布置为112m+208m+112m.主桁立面采用有竖杆的华伦式桁架，桁高10m，节间长度8m，中间支点处上加劲弦中心到上弦中心高度为28 m，上加劲弦采用二次抛物线，上弦杆与加劲弦杆之间用吊杆连接.主桁横向采用三桁结构，桁间距为18 m×2.主桁三片桁间仅在中间支点上加劲弦与上弦间的大竖杆处设有横向联结系，其他位置将竖杆与横梁联结成横向框架.主桁杆件为箱型截面整体节点结构，杆件之间采用高强度螺栓连接，预制桥面板与纵、横梁栓接.全桥布置如图1所示.

3.2 数值模型

由于自然环境激励能量有限，难以获取大桥的高阶振动频率.在试验过程中，主要目的是拾取竖弯、横弯和扭转的低阶模态，这些模态振型一般能够代表大桥的主振型.为提高测点的拾振效率，在模态试验之前，用桥梁专用有限元软件MIDAS/CIVIL 2006建立3种三维计算模型(编号分别为模型Ⅰ、Ⅱ、Ⅲ)分别进行初步仿真计算.3种模型均按设计的连续梁约束(中桁支座施加竖向和横向约束，两边桁支座施加竖向简单支撑，另靠莞城侧的3个次边墩再添加纵向约束)，3片主桁及平联均选用梁单元模拟，其不同之处为:模型Ⅰ为梁系模型，把各主桁及平联杆件以刚性连接模拟，预制栓接桥面板按等效节点荷载施加于该梁系结构上，而不另建桥面板单元;模型Ⅱ按实际尺寸建立桥面板单元，组成梁壳模型，上下弦杆和刚性悬索采用固接，桁架杆件与桥面板采取铰接;模型Ⅲ同模型Ⅱ一样建立梁壳模型，不同的是各构件间的连接方式均采用刚性连接.其中计算模型Ⅰ如图2所示.

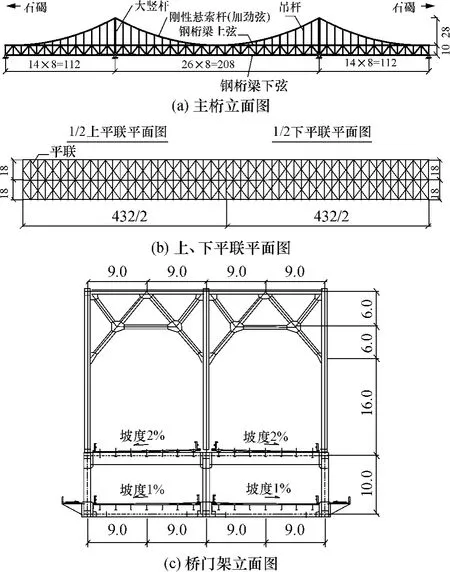
图1 全桥布置图(单位:m)Fig.1 Arrangement of the whole bridge(Unit:m)

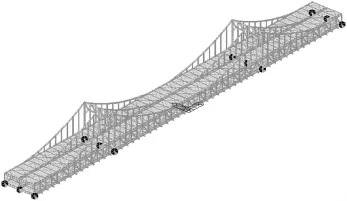
图2 有限元模型Fig.2 Finite element model

3.3 模态试验

通过计算，能够获得结构的理论自振频率和振型.依据初始计算结果和桥梁的结构特征布置拾振测点:在主桥上下两层桥面的边跨中桁和两边桁的L/4(L为大桥边跨的跨度)、L/2、3L/4处，以及中跨的l/6(l为大桥中跨的跨度)、l/3、l/2、2l/3、5l/6 处布置竖向振动的测点，共计66个竖向测点，拾振点及其编号如图3所示;在主桥上层桥面的中桁两边跨的支座，跨中以及中跨的l/4、l/2、3l/4处布置水平横桥向振动的测点，共计9个横向拾振测点，从石碣至莞城方向依次编号为H1至H9.

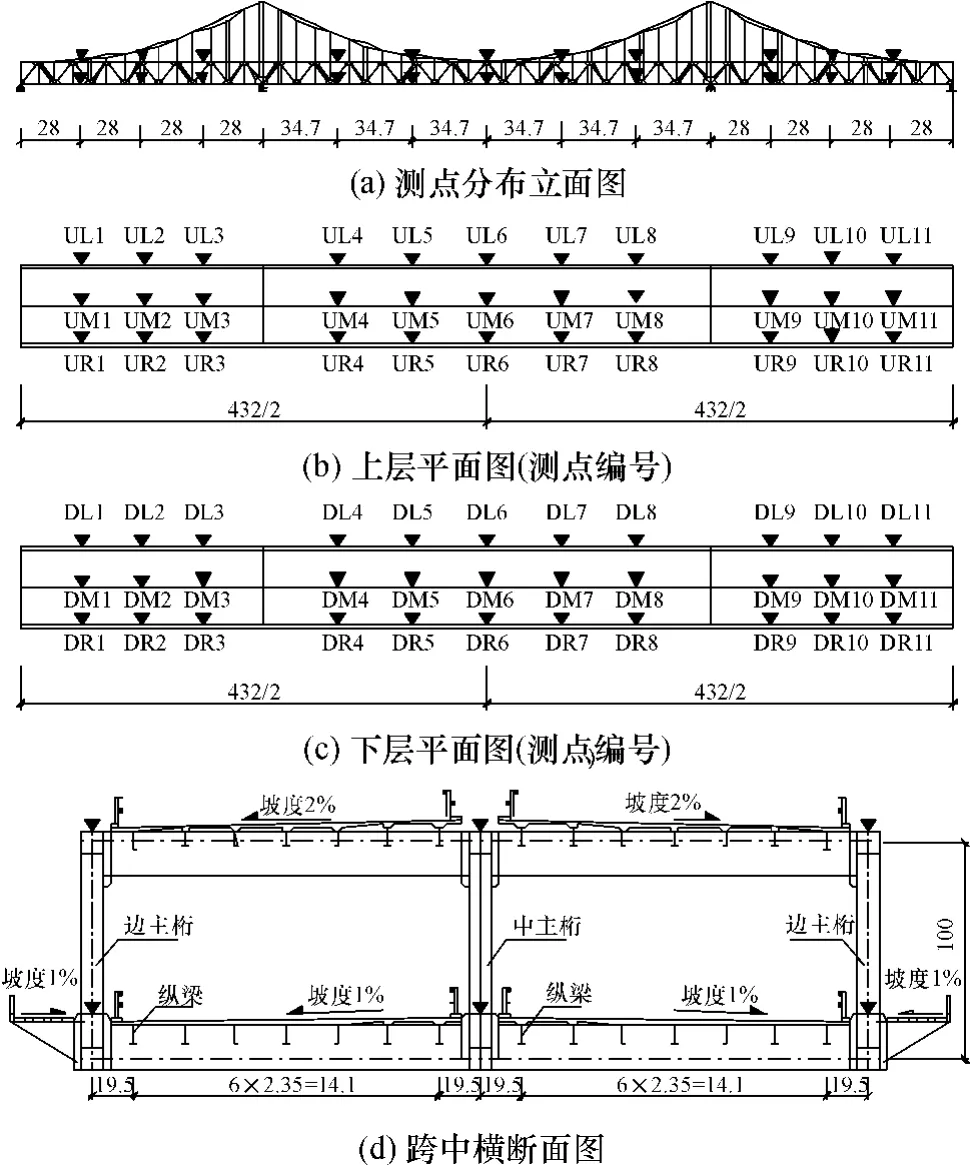
图3 竖向拾振点布置示意图(单位:m)Fig.3 Arrangement of vertical frequency pickup points(Unit:m)

由于测点数量较多，宜采用移动分组采样测量方式，每组测点采样时都同时对固定的基准参考测点(竖向为DR8测点、水平横桥向为H6测点)进行采样.采用哈尔滨工程力学研究所出产的941-B型水平向和垂直向伺服加速度传感器(频率为0.25～80.00Hz，灵敏度为10－5g)进行拾振，采样频率取为20.00Hz，持续测试0.5h.传感器拾得桥面随环境激励的加速度振动响应信号，通过放大器放大并滤波，再由多通道采集仪(北京东方振动和噪声技术研究所DASP 2006)采集并存储，然后选择平稳段进行模态识别分析.

4 结果与分析

把测试结果转换到频域进行模态识别分析，对于随机信号的处理，通常选用汉宁窗以减少功率谱泄漏，这也是文中的加窗方法，并采用3/4的重叠系数.先初步读取功率谱的峰值和频率，然后再把各动节点与固定节点进行互谱分析.其中DM1和DR8的时程曲线及其自谱曲线如图4所示，两者的互谱曲线、相干系数和相位差如图5所示.

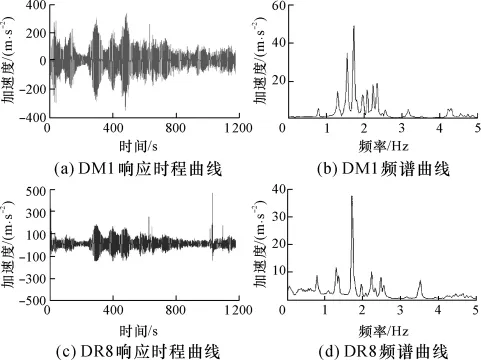
图4 DM1和DR8的响应时程及频谱曲线Fig.4 Response time and frequency spectrum curves of DM1 and DR8

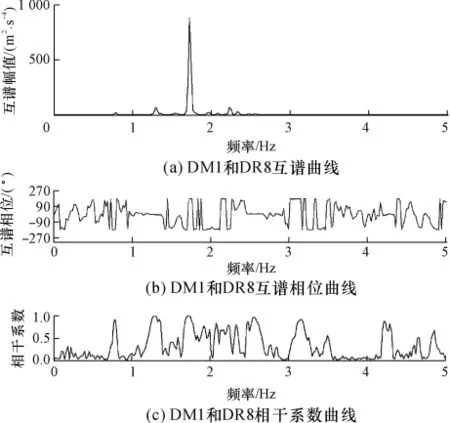
图5 DM1和DR8互谱分析Fig.5 Cross-spectrum analysis of DM1 and DR8

从图4中的时程曲线可以看出，外部激励较稳定，可选出一平稳段进行分析.在功率谱图中有很多峰值点，但所对应的频率未必都是固有频率.通过互谱分析(见图5)发现，在极值点对应的频率1.719Hz处，DM1和DR8的相位差为－176.2°，相关系数为0.995，这样就进一步确定了1.719 Hz为结构的某一阶固有频率.依此方法，低阶固有频率一般都能识别出来，所感兴趣的竖弯、横弯、扭转低阶频率及其相应的阻尼比如表1所示.

由3种理论模型计算所得的自振频率和实测振动频率见表2.从表2中可以看出:3种模型所计算的各阶自振频率值相差较大，模型Ⅰ和模型Ⅱ的计算结果均比模型Ⅲ小，且各阶相应频率的差值均在6.5%以上;模型Ⅲ的理论自振频率比相应实测结果略小，特别是前4阶，其误差在4%以内，属工程可接受范围.对比结果表明:在建模计算时，不能只计栓接桥面板的质量，而忽略其对整体刚度的贡献;各构件间的连接方式对整体计算结果影响较大，受整体节点加强作用的影响，三桁整体受力性能较好，栓焊杆系连接方式更接近于固结;对于成桥后整体静动力受力分析，刚性悬索和主桁杆件能用梁单元来模拟计算.模型Ⅲ的计算结果较实测值略小的主要原因是:在大桥的杆件连接中，采用了整体节点连接技术，且大节点板较多.如图6所示，在整体节点连接区域的杆件截面存在加大、加厚等复杂现象，而在理论模型中选用的梁单元未能考虑到这一特点.

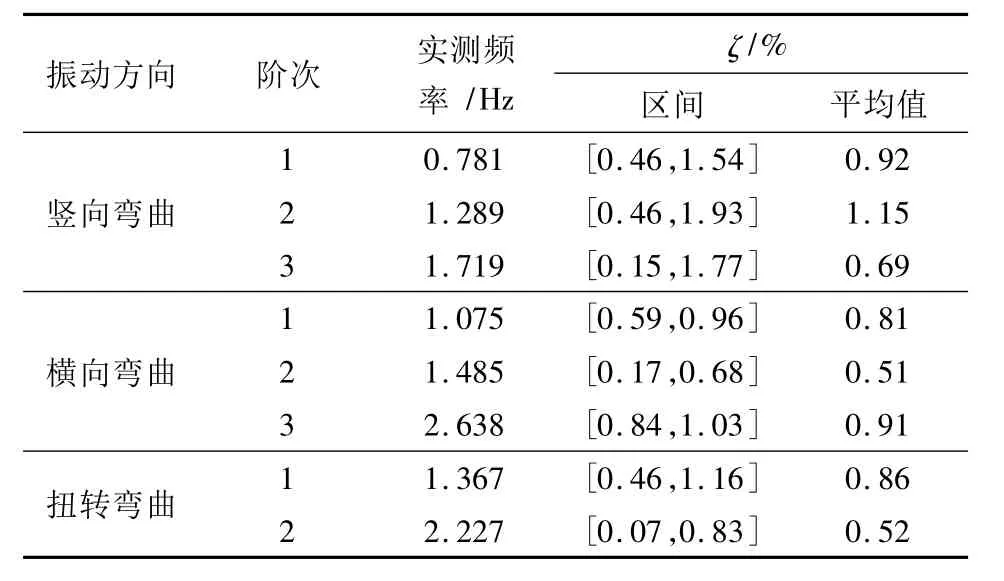
表1 实测振动频率及阻尼比Table 1 Tested modal frequencies and damping ratios

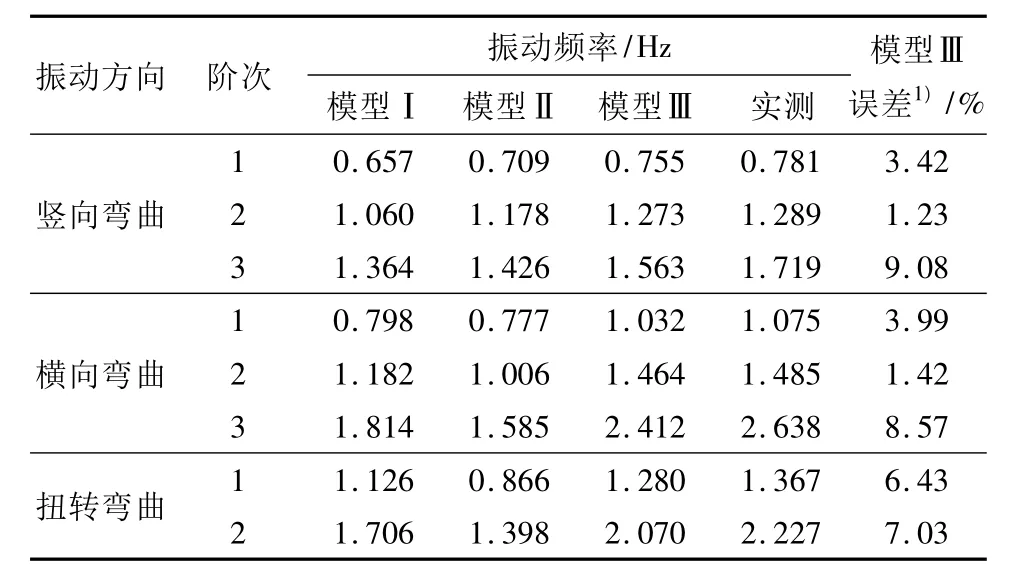
表2 理论自振频率和实测振动频率比较Table 2 Comparison of theoretical natural vibration frequencies with the tested ones

图6 整体节点Fig.6 Integral joints

对测试结果进行处理分析后，根据式(9)，可得到各移动测点与固定基准点在所获得的固有频率处功率谱的比值，再把这些比值归一化就可得到用这些离散点表达的结构振型.为了获得主梁完整的三维主要振型图，根据振动方程式(1)和结构的连续性假设，把所有测点的相对振幅作为一组强制位移施加于主梁结构上，由静力计算的各节点位移值作为结构振型的插值结果.通过理论模态计算和对测试结果的分析，可以绘出结构的振型，但限于篇幅和直观性，文中只绘出了钢桁梁的振型.前2阶竖向和扭转的理论模态和试验模态如图7－10所示.

由于横向拾振参考点接近横向第2阶模态振型的节点位置，即参考点所拾得的横向第2阶信号的信噪比较低，故只绘横向第1阶和第3阶的横向振型对比图.以中轴线中心为原点，纵桥向为X轴，经平滑处理后的横向对比振型见图11(a)和11(b).

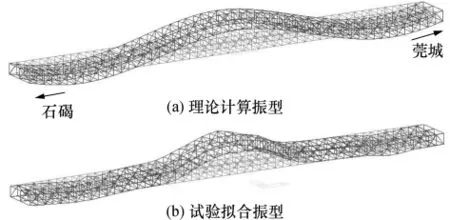
图7 竖向第1阶理论和试验振型Fig.7 Theoretical and experimental first-order vertical mode shapes

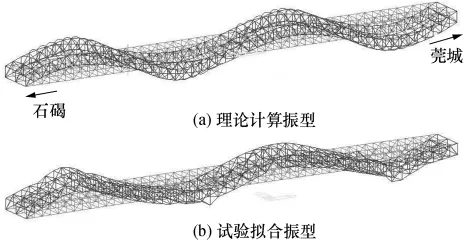
图8 竖向第2阶理论和试验振型Fig.8 Theoretical and experimental second-order vertical mode shapes

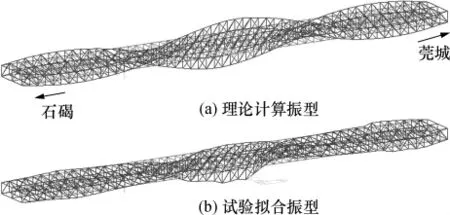
图9 扭转第1阶理论和试验振型Fig.9 Theoretical and experimental first-order torsional mode shapes

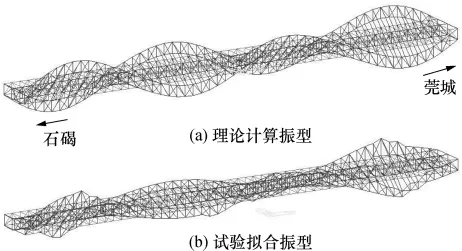
图10 扭转第2阶理论和试验振型Fig.10 Theoretical and experimental second-order torsional mode shapes

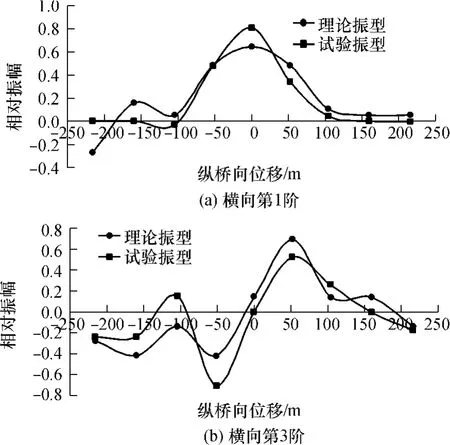
图11 横向第1、第3阶理论和试验振型Fig.11 Theoretical and experimental first-and third-order horizontal mode shapes

从图7－11的对比结果可以看出:竖向弯曲理论和试验振型吻合得很好，三桁结构整体受力性能较好;由于大桥的扭转刚度较大，扭转的信噪比较低，两者的大体形状吻合，实测中跨和边跨的振幅比与相应理论计算的振幅比存在一定差距;横向振型吻合较好，仅个别有较大差别，这与理论计算模型约束和实际非铰非固约束有些不符有关，因此难以真实地模拟横向约束.另外，由于试验持续时间较长，白噪声前提条件不能完全满足，因而会给模态参数识别带来少许误差.

5 结语

文中针对国内首座三桁刚性悬索加劲钢桁梁双层公路特大桥，基于环境激励法，采用移动分组采样测量的方式，较详细地介绍了模态试验过程，并采用频域识别法，获得了东莞东江特大桥所感兴趣的模态参数，然后直接在有限元模型上添加强制位移，以静力计算所得的节点位移作为振型的拟合值，得到了更加直观的三维连续振型.试验测试频率与三维有限元计算值总体上吻合得较好，特别是低阶模态(前4阶)，误差在4%以内.由试验值和理论值的对比结果可以发现，考虑预制栓接桥面板和将栓焊连接简化为刚性连接的模型Ⅲ更符合实际，三桁结构整体受力性能较好.对比结果同时表明，模型Ⅲ可作为成桥之初的基准有限元模型，用于大桥日后的健康监测、损伤识别和抗风稳定性分析.

［1］谭明鹤，王荣辉，黄永辉，等.刚性悬索加劲钢桁梁桥特殊节点模型试验［J］.中国公路学报，2008，21(1):47-52.Tan Ming-he，Wang Rong-hui，Huang Yong-hui，et al.Special joint model test of stiff suspension reinforced steel truss bridge［J］.China Journal of Highway and Transport，2008，21(1):47-52.

［2］顾培英，丁伟农.模态试验在梁损伤诊断中的应用研究 ［J］.振动与冲击，2004，23(3):60-63.Gu Pei-ying，Ding Wei-nong.Application of modal test in diagnosing damage of beam［J］.Journal of Vibration and Shock，2004，23(3):60-63.

［3］姚志远.大型工程结构模态识别的理论和方法研究［D］.南京:东南大学土木工程学院，2004.

［4］李德葆，陆秋海.实验模态分析及其应用［M］.北京:科学出版社，2001.

［5］李爱群，丁幼亮，费庆国，等.润扬大桥斜拉桥模态频率识别的环境变异性［J］.东南大学学报:自然科学版，2007，37(2):245-250.Li Ai-qun，Ding You-liang，Fei Qing-guo，et al.Environmental variability in modal frequency identification of Runyang Cable-Stayed Bridge［J］.Journal of Southeast University:Natural Science Edition，2007，37(2):245-250.

［6］任伟新.环境振动系统识别方法的比较分析［J］.福州大学学报:自然科学版，2001，29(6):80-86.Ren Wei-xin.Comparison of system identification methods using ambient vibration measurements［J］.Journal of Fuzhou University:Natural Science，2001，29(6):80-86.

［7］Lardies J.Modal parameter identification from output-only measurements［J］.Mechanics Research Communications，1997，24(5):521-528.

［8］Wu J R，Li Q S.Finite element model updating for a highrise structure based on ambient vibration measurements［J］.Engineering Structures，2004，26(7):979-990.

［9］Yang Y B，Chen Y J.A new direct method for updating structural models based on measured modal data［J］.Engineering Structures，2009，31(1):32-42.

［10］刘汉夫.铁路桥梁模态参数测试方法的探讨［J］.世界桥梁，2007(3):59-61.Liu Han-fu.Study of modal parameter yesting methods for railway bridges［J］.World Bridges，2007(3):59-61.