用蒙特卡洛法分析重庆至宜昌段月客流的概率分布

李 鑫

(武汉理工大学,湖北武汉 430063)

随着改革开放的深入,内河交通运输业得到了较大的发展,内河水域船舶的运行强度和密度增大,运量和运力也随之增加[1],同时由于内河船舶日夜航行,气候变化莫测,水位涨落不定,以及受航道条件限制的影响,致使交通事故频频发生。船舶是宜昌至重庆段两岸居民的重要交通工具及运输方式,该段水域复杂,客流量大,为切实加强水上交通安全管理,提高渡口、渡船安全管理水平,保障人民群众生命财产安全,本文对该水域的客流状况进行分析,为相关安全管理提供理论依据。

1 蒙特卡洛法分析的程序

1.1 目标函数的确定

针对重庆至宜昌段月总客流量进行统计分析,得出其概率分布、概率密度等相关数字特征。重庆至宜昌段月总客流量等于该段各分客流量之和,即等于重庆客流量、三峡客流量、宜昌客流量之和,其数学表达式为:

R=X+Y+Z

R-重庆至宜昌段月总客流量

X-重庆段月客流量

Y-宜昌段月客流量

Z-三峡段月客流量

X,Y,Z假设为相互独立的随机变量,通过对X,Y,Z的随机抽样得出R,并经过多次抽样得到一系列的R,程序框图如图1所示。

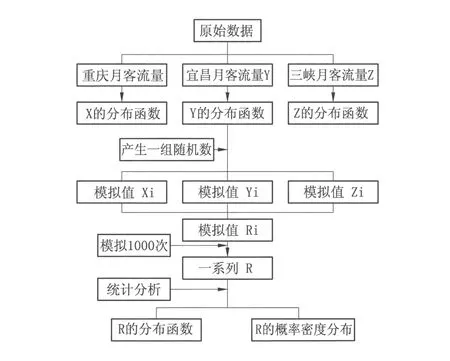
图1 程序框图

1.2 原始数据的整理

对于每个自变量,在其可能的取值范围内对其分组,每一组以其区间的中值为组标[1]。统计各段的频数,对每一组标定出其相应的概率,求出累积概率(见表1～表3),绘制其频数分布直方图(见图2),进而绘制其概率分布函数图(见图3)。

1.3 随机数的产生和X 、Y 、Z的选取

利用均匀分布随机数产生函数,一次产生一组随机数r(xi)、r(yi)、r(zi),根据随机数所落入的概率区间,来选取相应的 Xi、Yi、Zi的值。如 r(xi)=0.25,根据表1,可知其落入区间0.1739-0.6957,故应选取其相应的组标145为Xi的值。其模拟过程如表4所示。

图2 频数分布图

图3 概率分布函数

表1 重庆海事局客流量(X)的分布列与分布函数

表2 宜昌海事局客流量(Y)的分布列与分布函数

表3 三峡海事局客流量(Z)的分布列与分布函数

表4 三峡海事局客流量(Z)的分布列与分布函数

模拟次数i 随机数 月客运量X(万) 随机数 月客运量Y(万) 随机数 月客运量Z(万)总客运量R(万)..…… …… …… …… …… …… ……1000 r(x1000) X1000 r(y1000) Y1000 r(z1000) Z1000 R100

2 模拟的结果及分析

按照表5进行1000次模拟后可得一系列的R值,如图4。

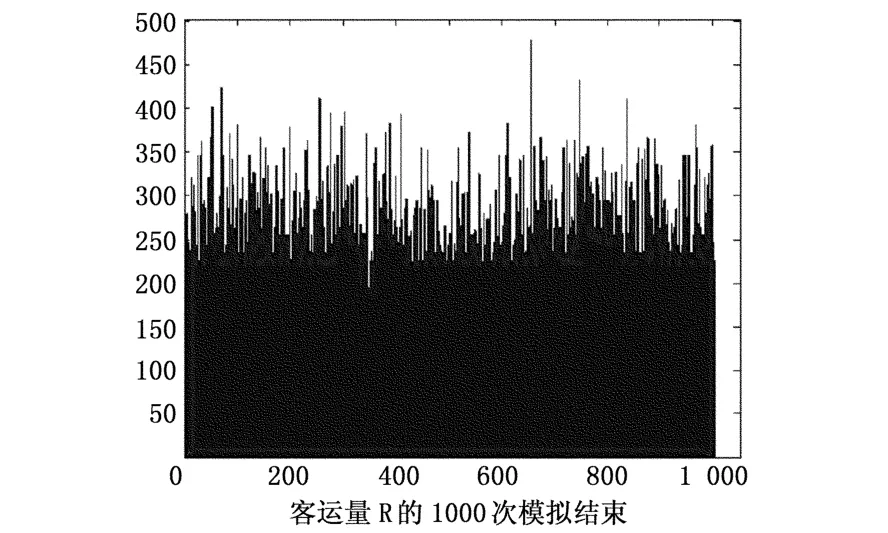
图4 客运量R的1000次模拟结果

得到重庆至宜昌段月客流量R的一系列值后,进行计算可得到其数学期望、方差、标准差分别为256.888,1946.846,44.123。

根据表5,可计算出R的累计概率,画出其概率分布函数图(见图4)如下:

现以R为横坐标,在各区间上画矩形,其面积等于R落入该区间的频率,便得到直方图(见图6),该图可近似表示R的概率密度分布[6]。

若作一参数u=256.888,ó=44.123的正态分布曲线,如图6中所示,可见随机变量R的密度分布是近似于正态分布的。

表5 模拟1000次后,总客流量R在各区间的频率

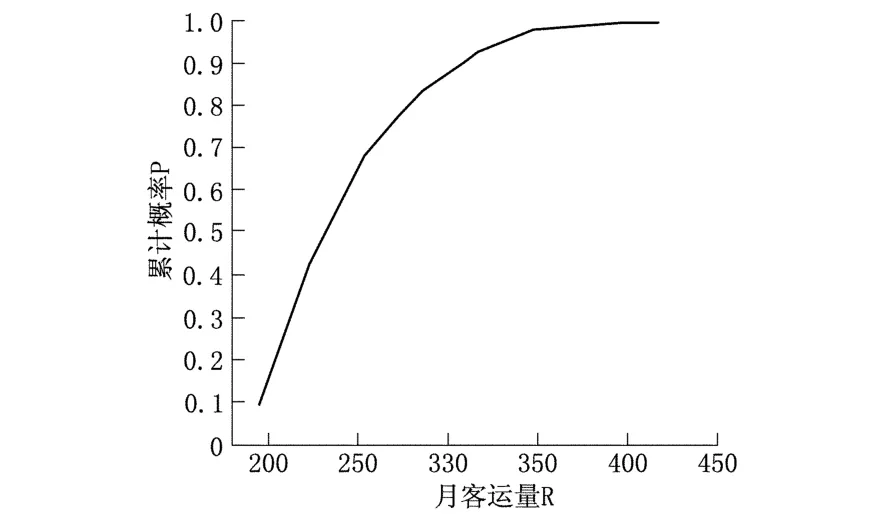
图5 月客流量R的概率分布函数图

3 结 语

本文结合长航实测统计的航段月客流量数据,运用蒙特卡洛等方法对重庆至宜昌段总月客流量进行了分析,并绘出了其概率分布函数图和概率密度分布图,得出重庆至宜昌段总月客流量近似地服从正态分布,从而为相关安全管理提供理论依据,以加强该水域的通航安全。

图6 月客流量R的概率密度分布

1 余 劲,张 玮,姜继红,廖 鹏.西江航道船舶流的概率分布特性[J].交通运输工程学报.2006,6(2)

2 江福才.回归分析在船舶安全航行中的运用[J].武汉交通科技大学学报.2000,6