遗传算法支持下的孔组复合位置度误差评判
张小萍, 王君泽, 周圣铧
遗传算法支持下的孔组复合位置度误差评判
张小萍, 王君泽, 周圣铧
(南通大学,江苏南通226019)
在孔组复合位置度误差评判过程中,用传统的数值优化方法一般难以找到符合最小条件判别准则的几何图框理想位置,尤其当位置度公差遵守最大实体要求且被测要素尚未达到最小实体尺寸时,被判为不合格的零件还有被修复的可能。针对上述问题,可利用自适应遗传算法全局搜索几何图框最佳位置,并在搜索过程中同时考虑遵守最大实体要求时的误差补偿因素的影响。此外,针对不合格零件进行的可修复性判别和修正量的计算,进一步降低了零件误废率。
机械设计;误差评判;遗传算法;复合位置度;孔组
复合位置度公差一般用来表示对成组要素(孔组或销组)位置加工精度的要求,其标注由上下框格组成。图1中所示为圆周分布孔组复合位置度公差标注,上框格表示整体要素对零件上其它要素(基准)的定位公差,下框格表示组内各要素对各自理想位置的定位公差,产品检验时,必须同时满足上下框格条件方为合格。根据国标《GB/T4249-2009产品几何技术规范(GPS)公差原则》的规定,当位置度公差遵守最大实体要求(MMC—Maximum Material Condition),且被测要素偏离最大实体状态时,位置度误差允许增大。因此,在此前提下被判为不合格的零件,只要各要素的尺寸尚未达到最小实体尺寸,就还有可能被修复。在生产中,对孔组位置度的检验通常是用位置量规来进行的。位置量规只能检验出该零件的孔组位置度误差是否合格,但不能给出误差的具体数值,当然更无从谈起对不合格零件的修复了。复合位置度误差的求解计算本质上属于非线性优化问题,由于非线性优化问题本身很难找到最优解,因此,与此相关的算法一直处于不断改进和发展之中。在国外,有E A Lehtihet,N U Gunasena等针对最大实体要求,建立了复合位置度误差的非线性规划模型,直接判断位置度误差是否合格;M J Kaisen提出用包容评定算法、L C R Carpinetti和D G Chetwynd提出用遗传算法求解复合位置度误差;此外,还有不少学者将人工智能、数理规划等理论引入到复合位置度误差的求解过程中来;在国内,刘永超、崔长彩等针对形位误差评定非线性化的特点,讨论了利用遗传进化理论求解几何产品形位误差的算法实现技术;粟时平、李圣怡等在非线性鞍点规划模型的基础上,讨论了利用遗传算法求解形位误差。但以上文献仅限于介绍形位误差计算的一般过程,而未有针对复合位置度具体实例。国内,仅见天津大学的何改云针对复合位置度误差评定提出了逼近算法。综观国内外,研究重点集中于采用何种模型、算法来描述、求解或评判位置度误差,一方面,有的算法结果只是近似符合最小条件定位误差原则;另一方面,未曾考虑最大实体要求时的误差补偿和可修复性判断。笔者也曾采用沿最大误差方向搜索的方法讨论矩形分布孔组位置度的误差评定与修正,但进一步研究发现该方法有可能在尚未搜索到最小条件理想位置时就停止了搜索,这样仍旧有可能造成部分零件的误废。针对上述问题,本文的研究目标如下:
(1)提供一种快速、准确、广泛适用的优化算法,求解满足最小条件下的复合位置度误差,并判别其合格性;
(2)对判为不合格的零件进行可修复性判断;若可修复,进行相关各孔修正量的计算,以达到减少误废、降低生产成本之目的。
遗传算法(GA—Genetic Algorithm)是21世纪有关智能优化计算中的关键技术之一,其主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不依赖于梯度信息,尤其适用于处理传统搜索方法难于解决的复杂和非线性问题。本文将遗传算法引入到复合位置度误差求解计算中来,并针对标准遗传算法的不足提出了改进。实验表明,改进的遗传算法可以高效、准确地解决此类问题。
1 遗传算法的改进
遗传算法是一种全局优化算法,但标准的遗传算法容易出现早熟现象,并且在进化后期搜索效率较低。为了获得更高的收敛概率和更快的收敛速度,需要对标准遗传算法加以改进。
在遗传算法的若干参数中,交叉概率和变异概率的选择是关键,它们直接影响着遗传算法的行为和性能。交叉概率越大,新个体产生的速度越快,然而交叉概率过大,高适应度的个体结构就会很快被破坏,交叉概率过小,又会使搜索过程缓慢以致停滞不前。对于变异概率来说,如果其取值过小,就不易产生新的个体,如果取值过大,遗传算法就会变成纯粹的随机搜索。针对这一问题,Srinvivas等人提出了自适应策略,即根据算法运行过程中提供的反馈信息,对交叉、变异概率做实时修正。当种群各个体适应度趋于一致或局部最优时,交叉、变异概率增加,而当种群各个体适应度比较分散时,交叉、变异概率减少。同时,对于适应度值高于平均水平的个体,对应于较低的交叉、变异概率,使该个体得以保护进入下一代,而低于平均水平的个体,对应于较高的交叉、变异概率,使该个体被淘汰。自适应遗传算法中交叉、变异概率P和P的计算公式如下

(2)
式中——群体中的最大适应值;f——群体平均适应值;——要交叉两个体中较大的适应度值;——要变异两个体中较大的适应度值;、、,为常数,<、<。由上式可见,应用自适应策略的遗传算法能够提供相对某个解的最佳交叉概率和变异概率。
2 基于自适应遗传算法的孔组复合位置度误差评判
孔组通常有矩形分布和圆周分布两种形式。本文以图1所示板形零件圆周分布孔组为例,讨论其复合位置度误差的评判与修正。

图1 圆周分布孔组复合位置度公差标注
2.1 误差评定目标函数的建立
图1中,上框格公差值为孔组整体要素位置度公差,其正确理论尺寸由几何图框1确定,它相对于基准位置固定;下框格公差值为孔组内各孔位置度公差,其正确理论尺寸由几何图框2确定,由于没有基准的约束,所以它既可以平移,也可以旋转(如图2所示)。在零件检测时,各孔实际中心轴线若同时落在上述两公差带的重叠部分,即为合格。
图1所示圆周分布孔组的位置度公差采用极坐标形式标注,几何图框1相对于基准的位置分别由正确理论尺寸1和2确定。误差评定时应将图样上各孔的极坐标值换算成直角坐标值。各孔的理论直角坐标值00可按式(3)确定
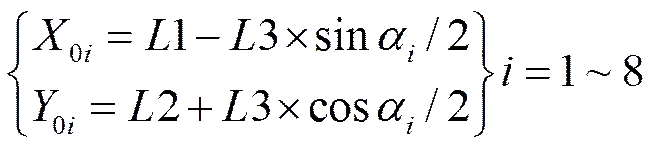
上式中1和2为孔组定位圆圆心的坐标值,3为定位圆直径,为各孔对应圆心角。若各孔中心实测坐标为(x, y),孔径尺寸为,直径偏差为dp。
图2 几何图框与公差带
由于确定孔组整体要素位置度的公差带相对于基准是固定的,因此,其合格性和可修复性判别相对简单,此处不再赘述。本文假设在孔组整体要素位置度合格或不合格但可修复的前提下,讨论孔组内各孔位置度误差的评判。
由于没有基准的约束,几何图框2既可以平移,又可以旋转。若记其平移增量为(Δ,Δ),旋转角度增量为Δ,此时几何图框2所确定各孔中心的正确理论坐标值应为

各孔实际中心距其理论正确位置的距离为
(5)
令

若(Δ, Δ, Δ)≤0,则该孔组内各孔位置度误差合格;
若(Δ, Δ, Δ)>0,则表示不合格。
此时,问题的本质已转化为如何寻找一组(Δ, Δ, Δ)值使得目标函数(Δ, Δ, Δ)值最小化。显然,这是一个三维非线性寻优问题,而遗传算法在解决这类问题时比传统的数值优化方法有着明显的优势。
2.2 位置度误差合格性评判过程
前已述及,基于自适应策略的遗传算法能够提供相对某个解的最佳交叉概率和变异概率,从而可以获得较高的收敛概率和收敛速度,本文采用这一算法评判孔组内各孔位置度误差具体过程如下:
(1)编 码
为避免传统遗传算法中二进制编码的不足,本文采用归一化实数编码,即rЄ[0,1]。对多维变量寻优,每个分量可以看作一个子个体,若某子个体的可行域为[U,V]则其所对应的变量值为r=U+(VU)·r¢。子个体的编码组成个体编码R=(¢,¢,…,r¢),为变量维数,本例为3,¢¢¢分别对应于变量Δ、Δ、Δ。若优化问题的寻优精度为10,则子个体编码长度为

本例寻优精度为10。
(2)确定相关参数,产生初始种群
本例中种群规模=50,最大迭代次数为500,杂交常数、取0.5、0.9,变异常数、为0.02、0.05。
在遗传算法中,对于多维寻优采用随机方法产生初始种群,有可能使种群分布不合理,从而导致算法陷入局部最优解。为有效避免这类问题的发生,可使初始种群在其可行域内均匀分布。若某变量对应的可行域为[U,V],则归一化实数编码的子个体初始种群为

则对应的变量值为
(9)
若变量维数为,则此时初始种群的规模为=·。显然,初始种群的均匀分布在改进遗传算法性能的同时也会使计算量成几何级数增加。为达到两者兼顾的效果,本例中,选择变量Δ、Δ对应子个体进行初始种群均匀化产生,Δ对应子个体初始种群随机产生。
(3)确定适应度函数
本文讨论的是最小化寻优问题,适应度函数为

式中为一大于()最大值的参数。
(4)计算个体适应度,并判断是否符合优化准则,若符合,输出最佳个体及其代表的最优解,转向(7);否则,转向(5)。
(5)依据适应度比例方法选择再生个体。
(6)按照式(1)、式(2)分别确定交叉、变异概率,在每一个分量对应的子个体间彼此独立地进行交叉、变异,产生新一代的种群,返回步骤(4)。
(7)此时,最优解所对应的适应度函数为()。
若()<,则零件孔组内各孔位置度误差不合格,进入可修复性判断阶段;
若()≥,则零件孔组内各孔位置度误差合格,具体数值为2´(())。
2.3 位置度误差可修复性评判
对位置度误差不合格的零件,若各孔孔径还未达到最小实体尺寸,则就还有被修复的可能。根据2.2节介绍的方法,只需将目标函数式(6)中的dp替换成,重复上述评判过程即可。只是在第(7)步中若(¢)<,表示零件不可修复;若(¢)≥,表示零件可修复。
对可修复零件,各孔修正量的计算可按如下步骤进行:
(1)根据第(7)步所得最优个体对应的最优解(Δ¢Δ¢Δ¢)确定各孔中心理论正确位置坐标为

令
(12)
(2)对孔组整体要素位置度误差合格的零件来说,只需比较dm和dp。若dm>dp,则该孔需修正,孔径应修正至(D+dm)~()。若dm≤dp,该孔不需修正。
(3)对孔组整体要素位置度误差不合格但可修复的零件来说,若将因整体要素位置度不合格而确定的各孔修正量记为ds,则需比较max(dm, ds)与dp。若max(dm,ds)>dp,该孔需修正,孔径应修正至(max(dm, ds))~()。若max(dm, ds)≤dp,该孔不需修正。
3 应用实例
有如图1所示板形零件圆周分布6孔组,孔组定位尺寸1和2分别为80mm、60mm,孔组分布圆周直径3为50mm,孔径尺寸为,复合位置度公差上框格值为0.20,下框格值为0.10,各孔实际测量尺寸如表1所示。程序运行结果:几何图框2平移旋转增量(Δ, Δ, Δ)对应最优解为(0.0032, 0.0008, 0.0002),各孔实际中心距其理论正确尺寸的距离d分别为0.0569、0.0178、0.0593、0.0576、0.0532、0.0589,(d–(TS+dp)2)≤0 (=1~6),孔组复合位置度误差合格。实验100次。最大迭代次数373次,最小迭代次数210次,平均迭代次数275次。
又有图1所示板形零件圆周分布8孔组,孔组定位尺寸1和2分别为100mm、50mm,孔组分布圆周直径3为40mm,孔径尺寸为,复合位置度公差上框格值为0.18,下框格值为0.10,各孔实际测量尺寸如表2所示。程序运行结果:孔组整体要素位置度误差合格,孔组内各孔位置度误差不合格,但可修复。第2、4、6、7号孔需修正,修正后孔径偏差应分别在0.035~0.048、0.032~0.048、0.019~0.048、0.028~0.048之间。实验100次,合格性判断过程中最大迭代次数378次,最小迭代次数256次,平均迭代次数312次;可修复性判断过程中,最大迭代次数346次,最小迭代次数232次,平均迭代次数296次。
4 结束语
本文针对圆周分布孔组复合位置度误差评定模型非线性化的特点,采用自适应遗传算法直接求解符合最小条件评定准则的孔组内各孔位置度误差值,精度高、速度快。同时该算法对矩形分布孔组复合位置度误差评定同样适用。系统提供的可修复性评判功能则进一步减少了不合格产品的产生,降低了生产成本。本文的研究成果为生产企业准确、快速评定成组要素的复合位置度误差提供了一种新的有效手段,具有显著的实际意义。

表1 孔组测量数据一 mm
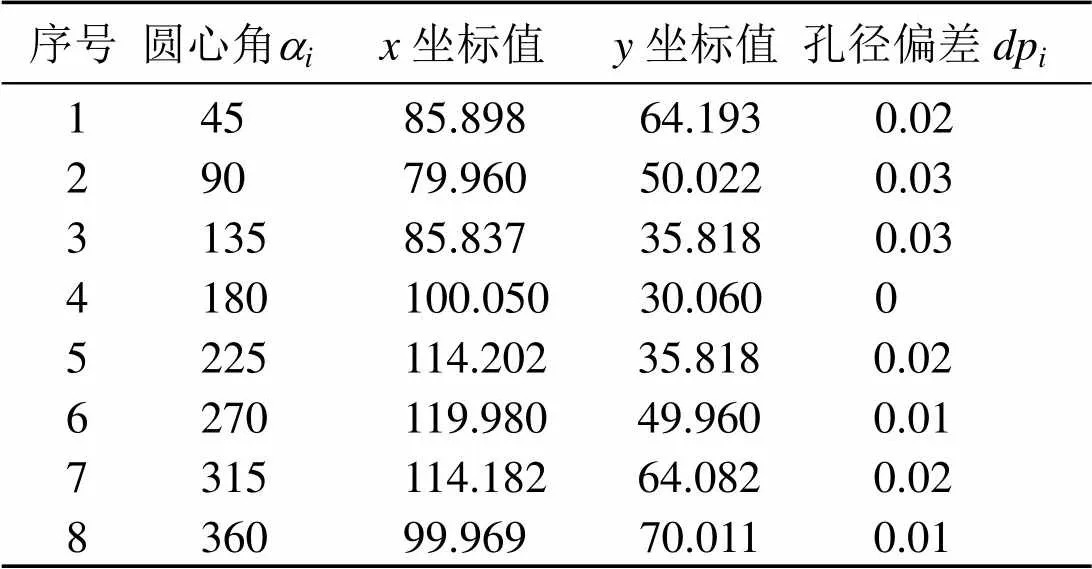
表2 孔组测量数据二 mm
[1] GB/T4249-2009, 产品几何技术规范(GPS)公差原则[S].
[2] Lehtihet E A, Gunasena N U. On the composite position tolerance for patterns of holes [J]. Annals of the CIRP, 1991, 40(1): 33-37.
[3] Kasier M J. The containment model for composite positional tolerance evaluation. precision engineering [J]. 2000, 24(4): 291-301.
[4] Carpinetti L C R, Chetwynd D G. Genetic search methods for assessing geometric tolerances [J]. Computer Methods in Applied Mechanics and Engineering, 1995, 122: 193-204.
[5] Wilson R H, Latmobe J C. Geometric reasoning about mechanical assembly [J]. Artificial Intelligence, 1994, 71(2): 371-396.
[6] 刘永超, 陈 明. 形位误差的进化算法[J]. 计量学报, 2001, 22(1): 18-22.
[7] 崔长彩, 黄富贵, 张认成. 基于遗传算法的几何产品形位误差计算[J]. 微计算机应用, 2009, 30(4): 7-11.
[8] 粟时平, 李圣怡, 王贵林. 基于鞍点规划法的形位误差计算机评定[J]. 计量学报, 2003, 24(1): 26-28.
[9] 何改云. 形位误差的逼近原理及算法研究[D]. 天津:天津大学, 2006.
[10] 王君泽, 张小萍. 矩形分布孔组位置度计算机辅助评定[J]. 制造技术与机床, 1998, (4): 28-30.
[11] 陈国良, 王煦法, 庄镇泉, 等. 遗传算法及其应用[M]. 北京: 人民邮电出版社, 2001. 195-237.
Evaluating for Composite Position Error of Hole Group Supported by Genetic Algorithm
ZHANG Xiao-ping, WANG Jun-ze, ZHOU Sheng-hua
( Nantong University, Nantong Jiangsu 226019, China)
In the evaluating process of hole group composite position error, the traditional numerical optimization methods are generally difficult to find an ideal location for the geometric frame to meet the minimum condition criterion, especially when the position tolerance follows the principle of MMC and the measured features still do not reach the minimum material size, parts judged unqualified may also be repaired. Aiming at solving the above-mentioned problems, the adaptive genetic algorithm is proposed to search the best location for geometric frame globally, and at the same time, the error compensation due to following MMC principle is taken into account while searching. In addition, the repair-ability judgment and correction calculation are also carried out against failed parts, which will further reduce the false rejection.
mechanical design; error evaluation; genetic algorithm; composite position; hole group
TH 161
A
1003-0158(2011)03-0023-05
2009-12-26
南通市应用研究计划资助项目(K2009022);江苏省高校自然科学基础研究资助项目(07KJD540178)
张小萍(1973-),女,江苏江都人,副教授,硕士研究生,主要研究方向为计算机图形学、CAD。

