纵向弹性索对斜拉桥稳定性的影响★

刘芳平

0 引言

大跨度斜拉桥在设计，施工时一般在桥塔下设置一定数量的纵向弹性索来对主梁进行纵向约束形成漂浮体系加纵向弹性索约束的结构形式，即半漂浮体系。附加弹性索的弹性约束相当于在塔梁之间设置了一定弹性刚度的弹性联系，使得其弹性恢复力是塔梁相对位移的函数，其实施简单，但是对改善超大跨径的斜拉桥稳定性的效果是否显著，至今尚未研究。因此，开展这方面的研究对于超大跨径的斜拉桥找出比较理想的结构体系具有重要意义。本文结合重庆一座大跨径预应力混凝土斜拉桥——奉节长江大桥，用ANSYS非线性有限元程序，对结构有无弹性索的失稳模态和稳定性进行了数值模拟分析，比较了弹性索对斜拉桥稳定性的影响。最终研究表明，弹性索对斜拉桥的稳定性有一定提高。结构无纵向弹性约束时斜拉桥一阶线性失稳模态沿纵桥向飘逸，有弹性索作用时为主梁下挠失稳。在两种情况下，非线性失稳模态均为主梁跨中下挠失稳。纵向弹性索对稳定性的影响是通过对主梁纵向漂浮约束的大小程度产生影响的。对于超大跨径的斜拉桥想要得到较理想的结构体系还必需从纵向弹性索的设置方面进行详细研究［1，2］。

1 斜拉桥稳定问题ANSYS计算方法

从有限元计算的角度看，分析桥梁结构极限承载能力的实质就是通过求解计入几何非线性和材料非线性对结构刚度矩阵的影响，根据平衡方程，寻找其极限荷载的过程。桥梁结构在不断增加的外载作用下，结构刚度不断发生变化。当外载产生的压应力或剪应力使得结构刚度矩阵趋于奇异时，结构承载能力就达到了极限，此时的外荷载即为结构的极限荷载。

现定义结构在丧失承载能力前所能承受的荷载量与设计荷载量的比值为整体非线性失稳安全系数，即:

其中，{Pcr}为某工况下结构在失稳时的总荷载(包括恒载、活载);{Psj}为某工况下结构设计荷载(包括恒载、活载);λ为稳定承载能力安全系数，λ=λ0+λ1，λ0为设计荷载时基本安全系数，λ0=1，λ1为迭代分析得出的荷载系数，即结构的安全储备。

由此可知，结构的稳定性与结构的极限承载力是等价的，结构的非线性稳定分析与结构的非线性强度分析是统一的，它们统一于增量加载过程中，当荷载加载倍数λ=λ0=1时的非线性计算结果即为结构在实际荷载作用下的结构非线性变形和受力状态。

ANSYS无法直接得出非线性稳定分析的屈曲系数，也即上式中的λ值，而是借助于屈曲分析中对结构的逐步加载得到的荷载—位移曲线，判断结构的失稳点，从而计算出屈曲系数。

从上面所述可以看出，桥梁结构的极限承载能力既不同于通常所认为的强度问题，又与结构的强度(结构的应力水平)有着紧密的联系。也可以认为第二类稳定问题的本质在于求解结构在受荷载全过程中荷载—位移曲线。通常来说求解荷载—位移曲线可以采用位移增量法求解［3］。

2 工程实例分析

2． 1 工程概况及有限元计算模型

奉节长江大桥是一座大跨径的预应力混凝土斜拉桥，桥全长893 m，主跨460 m，跨径布置采用不对称5跨布置，即(30．4+202．6+460+174．7+25．3)m，桥宽20．5 m。

主塔为A形塔，采用C50混凝土，分上塔柱、横梁、中塔柱、盖板、下塔柱五部分，下塔柱为单箱三室截面，上、中塔柱为单箱单室截面。主梁除跨中112．6 m为C60混凝土外，其他都是C50混凝土，边跨采用箱梁，其余为∏形梁。斜拉索为空间双索面，共224根斜拉索，每塔每索面共28对斜拉索。下部结构共有6个桥墩，两边是边墩，最中间的两个是主塔墩，其余两个是辅助墩。

设计荷载:汽车—超20，挂车—120。

本桥采用鱼骨梁模式来模拟全桥进行空间分析。边墩、辅助墩仅考虑其对主梁的支撑和约束作用。主塔为钢筋混凝土矩形空心结构，采用Beam188单元模拟。主梁简化为鱼骨模型中的鱼骨，在有限元分析中采用Beam188单元模拟。在有限元模型中，主梁与斜拉索之间的连接即鱼骨模型中的鱼刺，为大刚度杆件，用Beam4单元进行模拟。斜拉索只承受拉力，抗压刚度很低。模型中采用Link10单元进行模拟。全桥有限元模型共有1 007个节点，840个单元。有限元模型见图1。

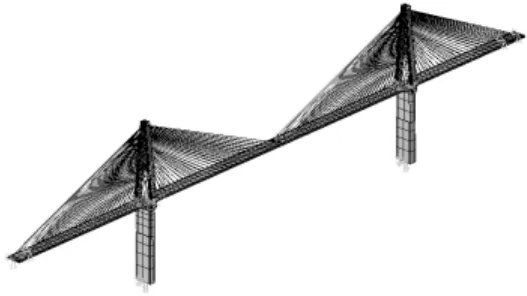
图1 大桥有限元分析模型

2． 2 不同分析工况说明

在进行稳定性分析时考虑的荷载包括一期恒载(自重)、二期恒载(桥面铺装等)、压重、斜拉索预应力、纵横向撞击力、水流力、侧向风荷载、活荷载(车辆、人群)等。荷载都是按照设计和规范进行取值。工况1:(有弹性索)实际成桥状态下，主梁与塔交叉处设置8根30 m长的纵向弹性索，从而形成半漂浮体系。主梁与墩塔间的8根弹性索用杆单元(Link10)模拟。在 ANSYS中，Link10为三维仅受拉或仅受压杆单元，独一无二的双线性刚度矩阵特性使其用只受拉选项时，如果单元受压，刚度就消失。工况2:(无弹性索)在成桥状态下，去掉8根30 m长的纵向弹性索，去掉索塔处主梁下面设置的竖向支承，只有塔墩固结，塔梁分离，主梁除辅助墩有支承外，其余全部由拉索支承，主梁成为纵向可浮动的一根具有多点弹性支承的梁，结构体系将变为漂浮状态。

2． 3 计算结果

分析中进行了汽车荷载全桥布置下，在有无弹性索两种工况下进行了线性和非线性稳定分析计算，各工况不同状态下的线性和非线性稳定安全系数见表1。

表1 两种工况下线性和非线性稳定系数

图2 无弹性索线性失稳模态

1)从表1数值可知，当结构增加纵向弹性约束的时候线性稳定安全系数增加了将近60%。从图2和图3比较得知，斜拉桥一阶线性失稳模态从没有弹性索作用时的沿纵桥向飘逸变为有弹性索作用时主梁下挠失稳。失稳模态发生质的变化，失稳模态的差别造成线性失稳值的差异。2)从表1数值可知，在两种情况下，非线性失稳值相差并不大，稳定安全系数仅增加了15%。从图4，图5可知，非线性失稳模态相近，均为主梁的跨中下挠失稳。

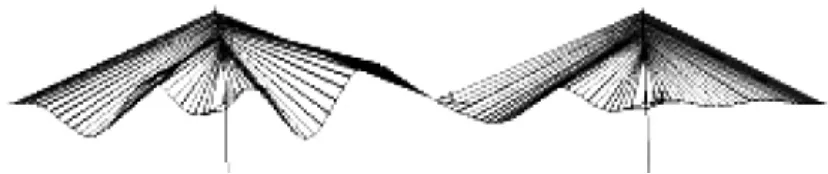
图3 弹性索线性失稳模态

图4 无弹性索结构非线性失稳模态

图5 有弹性索结构非线性失稳模态

3 结论及建议

1)结构无纵向弹性约束时斜拉桥一阶线性失稳模态沿纵桥向飘逸，有弹性索作用时为主梁下挠失稳。并且有纵向弹性约束时的线性稳定安全系数相对没有时提高较大。在两种情况下，非线性失稳模态均为主梁跨中下挠失稳，且稳定安全系数提高相对较小。2)纵向弹性索对稳定性的影响是通过对主梁纵向漂浮约束的大小程度产生影响的，本文只讨论了有无弹性索、弹性索布置特定的一种情况，其实弹性索设置的长短、位置、数量等因素都对斜拉桥的稳定性有影响，由于篇幅在本文中未详加讨论。对于超大跨径的斜拉桥想要得到较理想的结构体系还必需从这些方面进行详细研究［4］。超大跨径斜拉桥不同于常规跨径斜拉桥，各个体系在恒载和活载作用下稳定性都有所不同。针对不同特定漂浮体系、半漂浮体系和固结体系斜拉桥各自的稳定性在文献中分别进行过详细研究。但是对于同一座桥梁，哪一种结构体系的稳定性较好，什么样的超大跨径预应力混凝土斜拉桥结构体系比较合理，以便为桥梁设计施工提供重要的理论依据。选择合理的能够改善结构稳定性能的约束方式至关重要。有关不同体系斜拉桥稳定性的研究仍然是空白。

［1］ 项海帆．高等桥梁结构理论［M］．北京:人民交通出版社，2001．

［2］ 肖汝诚．确定大跨径桥梁结构合理设计状态的理论与方法研究［D］．上海:同济大学，1996．

［3］ 朱伯芳．有限元法原理与应用［M］．北京:中国水利水电出版社，1998．

［4］ 徐利平．超大跨径斜拉桥的结构体系分析［J］．同济大学学报，2003(4):400-403．