中考综合题及其求解策略
225754 江苏省兴化市垛田初级中学 沈 刚225700 江苏省兴化市教育局教研室 陈德前
所谓综合题,是指涉及的数学知识比较广泛,运算、论证、作图等比较复杂,需要灵活运用多方面的数学知识和熟练地技能技巧才能解答的问题.综合题不等于难题,有些竞赛题需要用某种特殊解法,但涉及的知识并不多,不能称为综合题.我们这里所谈的综合题,相当于中考试卷中的最后几道题.
综合题具有串联数学基础知识和基本技能、灵活运用解题方法、进行多层次思维训练、提高综合运用能力这样一些明显功能.因此,加强综合题的解题训练,有利于将所学的数学知识和技能融会贯通,起到复习、巩固、拓展、提高的作用,也有利于提高分析问题和解决问题的能力.要能顺利地解答综合题,必须深刻地、透彻地理解基础知识,掌握各个知识点之间的相互联系,还必须具备扎实的解题基本功,掌握好各种基本的解题方法与技巧.综合题的解题过程一般都比较复杂,有时需要经过迂回曲折的途径才能达到目的.有些综合题中还隐含着不易发现的隐含条件.这就要求我们在解综合题时,首先要认真审题,通过观察、分析,找出其中的难点所在,并通过联想(猜想)与概括,发现隐含条件,理顺解题思路,设计解题方案,而且在思考问题时,应尽量做到全面些、深刻些、灵活些.
初中数学综合题从知识科目上分有单科综合题和多科综合题,从题目形式上分有单一题和组合题.解综合题的基本方法就是把综合题分解为单一的基本题,把复杂图形分解为基本图形来处理.本文以中考题为例进行说明.
例1(2010年广州市)如图1,⊙O的半径为 1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是弧上的任一点(与端点A,B不重合),DE⊥AB于点E,以点D为端点,DE长为半径作⊙D,分别过点A,B作⊙D的切线,两条切线相交于点C.

图1
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;

1 分析
这是一道与圆相关的几何学科的综合题,考查了圆中的众多知识和一些基本的数学思想方法,涉及到的知识点有垂径定理、勾股定理、圆周角和圆心角定理、切线的性质定理、切线长定理、三角形内切圆的性质、两圆的位置关系、三角形面积等,考查的数学思想方法有转化思想、方程思想、建模思想、不变量思想等.解决这个问题的关键是将这道综合题分解为一系列的基本题,在解决了这些基本题后,问题就迎刃而解了.
2 基本题
基本题1
如图2,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,垂足为E,求弦AB的长.


图2
基本题2
如图3,点P是⊙O上一点,弦AB垂直平分线段OP,点D是上的任一点(与端点A,B不重合),求∠ADB的大小.
点评这是考查圆周角性质应用的问题,人教版九年级上册课本在第94页,第95页,第130页等处多次出现过这样的问题,特别是图3中的四边形APBO与第95页的第10题完全相同,因此易求∠ADB=∠APB=120°.
基本题3
如图4,⊙D是△ABC的内切圆,∠ADB=120°,求∠ACB的大小.


图4
基本题4
如图4,△ABC中,AB=,∠ACB=60°,⊙D是△ABC的内切圆,DE⊥AB于点E,设DE=r,试用含r的代数式表示△ABC的周长.
点评这是考查切线长定理的问题,人教版九年级上册课本在第105页,第106页,第110页,第112页等处多次出现过这样的问题.
设AC,BC分别切⊙D于F,G,由切线长定理可知
AF=AE,BG=BE,CF=CG,CD平分∠ACB.
因为AB=,∠ACB=60°,
所以AB+AF+BG=2,∠ACD=∠DCB=30°,又DF⊥AC于点F,DF=r,
所以CF=CG=r,
所以△ABC的周长 = 2+2r.
基本题5
如图 5,△ABC中,AB=,∠ACB=60°,⊙D是△ABC的内切圆,DE⊥AB于点E,记△ABC的面积为S,若求△ABC的周长.
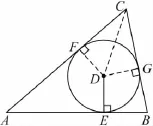
图5

又由基本题4可知AB+BC+AC= 2+ 2DE,


至此,这道综合题的解题思路已清晰显现,完整的解题过程如下.
3 求解
解(1)如图 6,连接OA,取OP与AB的交点为F,则有OA=1.
∵弦AB垂直平分线段OP,


图6
在Rt△OAF中,

∴AB=2AF=.
(2)∠ACB是定值.
理由:由(1)易知,∠AOB=120°,
因为点D为△ABC的内心,
所以连接AD,BD,
则∠CAB=2∠DAE,∠CBA=2∠DBA,

所以∠CAB+∠CBA=120°,
所以∠ACB=60°;
(3)记△ABC的周长为l,取AC,BC与⊙D的切点分别为G,H,连接DG,DC,DH,则有DG=DH=DE,DG⊥AC,DH⊥BC.


∵CG,CH是⊙D的切线,


∴CH=CG=DE.
又由切线长定理可知AG=AE,BH=BE,
∴l=AB+BC+AC= 2+ 2DE=8DE,



图7
例2(2011年衢州市)已知两直线l1,l2分别经过点A(1,0),点B(-3,0),并且当两条直线同时相交于y轴正半轴的点C时,恰好有l1⊥l2,经过点A,B,C的抛物线的对称轴与直线l1交于点K,如图7所示.
(1)求点C的坐标,并求出抛物线的函数解析式.
(2)抛物线的对称轴被直线l1,抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由.
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M.请找出使△MCK为等腰三角形的点M.简述理由,并写出点M的坐标.
1 分析
这是一道中考压轴题,是多学科的综合题,考查了代数中的点的坐标、一次函数、二次函数、方程(组)、两点之间的距离,几何中的三角形三边之间的关系、勾股定理、等腰三角形、相似三角形以及三角函数等知识,涉及到的数学思想方法有分类思想、数形结合思想、转化思想、方程思想等.解决它的关键是将它分解为基本题,可分解为如下一些基本题.
2 基本题
问题1在△ABC中,∠ACB=90°,CO⊥AB于点O,若OA=1,OB=3,求OC的长;
问题2已知两直线l1,l2分别经过点A(1,0),点B(-3,0),并且当两条直线同时相交于y轴正半轴的点C时,恰好有l1⊥l2,求点C的坐标;
问题3求经过点A(1,0),点B(-3,0),点C(0,)的抛物线的函数解析式;
问题4已知两直线l1,l2分别经过点A(1,0),点B(-3,0),相交于点C(0,),求直线l1,l2的函数解析式;

问题7已知△CKM,点C(0,),K(-1,2),M(-1,m),请求出使△MCK为等腰三角形的m的值.
3 求解
(1)解法1由题易知△BOC∽△COA,

∴点C的坐标是(0).由题意,可设抛物线的函数解析式为y=ax2+bx+,把A(1,0),B(-3,0)分别代入y=ax2+bx+,得

解法2由勾股定理,得
(OC2+OB2)+(OC2+OA2)=BC2+AC2=AB2,
又∵OB=3,OA=1,AB=4,
∴OC=-,
∴ 点C的坐标是(0).
由题意可设抛物线的函数解析式为

把C(0,)代入得a=-,
所以抛物线的函数解析式为

(2)解法1截得三条线段的数量关系为KD=DE=EF,理由如下:

由此可求得点K的坐标为(-1,2),


点F的坐标为(-1,0),
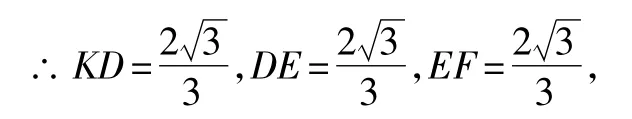
∴KD=DE=EF;
解法2截得三条线段的数量关系为KD=DE=EF,理由如下:
由题意可知 Rt△ABC中,∠ABC=30°,∠CAB=60°,



(3)当点M的坐标分别为(-2,),(-1,)时,△MCK为等腰三角形.理由是:
解法1(ⅰ)以点K为圆心,线段KC长为半径画圆弧,交抛物线于点M1,由抛物线对称性可知点M1为点C关于直线x=-1的对称点,所以点M1的坐标为(-2,),此时△M1CK为等腰三角形;
(ⅱ)当以点C为圆心,线段CK长为半径画圆弧时,与抛物线交点为点M1和点A,而三点A,C,K在同一直线上,不能构成三角形;
(ⅲ)作线段KC的中垂线l,由点D是KE的中点,且l1⊥l2,可知l经过点D,

解法2当点M的坐标分别为(-2,),(-1,)时,△MCK为等腰三角形.理由如下:
(ⅰ)连接BK,交抛物线于点G,易知点G的坐标为(-2,).
又因为点C的坐标为(0,),则GC∥AB.
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形,
∴△CGK为正三角形,
∴当l2与抛物线交于点G,即l2∥AB时,符合题意,此时点M1的坐标为(-2,);


(ⅲ)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,但点A,C,K在同一直线上,不能构成三角形.综上所述,当点M的坐标分别为(-2,),(-1,)时,△MCK为等腰三角形.
由上可见,解综合题的基本方法就是把综合题分解为单一的基本题,解决了这些单一的基本题,就可以它们为基础,当作零件,算成半成品或标准件,用到综合题中去,进行复合,就可以形成综合题的解题思路.因此,在平时的教学中要通过典型试题的分析,帮助学生掌握将综合题分解为基本题的方法与技巧,使学生能切实掌握,灵活应用,以提高学生解综合题的能力.

