同一个问题 不同的角度

430040 武汉市吴家山第三中学 吴 波

越来越多的中考压轴题，在二次函数的图象抛物线上架构几何图形，学生感觉难度较大，主要原因是思维水平跟不上.本文就充分应用习题，最大限度发挥习题的效应，发展学生的思维作一抛砖引玉，以期待各位同仁的指导.

题目如图1，抛物线y=－x2+2x+3与x轴交于A，B两点，交y轴正半轴于C点，D为抛物线的顶点，点P在OB的延长线上，且∠PCB=∠CBD，求点P的坐标.

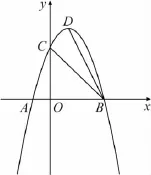
图1

1 不同的角度求解，培养学生求异思维

前期基础分析已知抛物线解析式，能够求出A，B，C，D四点的坐标，A(－1，0)，B(3，0)，C(0，3)，D(1，4)，要求点P的坐标，由于点P的位置在x轴上，可将其坐标转化成求线段OP的长，或者把点P看作某条直线与x轴的交点，我们需要求出这条直线的解析式.

思路1首先根据点C，点B的坐标，发现∠OBC=∠OCB，那么它们的邻补角也相等.结合条件∠PCB=∠CBD，那么涉及到的∠PCB和∠CBP构成了△PCB，以它为模板构造三角形全等.

略解1(如图2)延长BD交y轴于点Q.

∵OC=OB，

∴∠OBC=∠OCB，

∴∠CBP=∠BCQ，

又BC=CB，∠PCB=∠CBQ，

∴△CBP≌△BCQ，

∴BP=CQ，∴OP=OQ，

∵B(3，0)，D(1，4)，

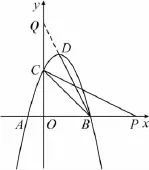
图2

∴直线BD的解析式为y=－2x+6，

∴Q(0，6)，

∴P(6，0)

思路2(如图2)发现∠OCB=∠OBC后，结合∠PCB=∠CBD，可以得到∠PCO=∠DBO，而∠PCO，线段OP可以得到直角△PCO，以它为模板构造三角形全等.

略解2同上解，证△COP≌△BOQ即可.

点评上述两种思路，将点P的坐标转化成求线段的长度，将线段置入三角形，构造出三角形全等，利用已知坐标求出线段的长，思维流畅，构造顺理成章.

思路3(如图3)由∠PCB=∠CBD，若标出PC与BD的交点M，则可得到MC=MB.容易得到∠MCO=∠MBO，若连接OM，得到△OMC≌△OMB.若能求出点M的坐标，就可以求出直线CM的解析式，从而求出点P的坐标.

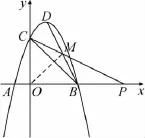
图3

略解3连OM，易证△OMC≌△OMB，

∴∠COM=∠BOM，

∴直线OM的解析式为y=x，

易知直线BD的解析式为y=－2x+6，

∴M(2，2)，又C(0，3)，

∴P(6，0).

点评从解析法的角度开始思考问题，关键是找出直线PC上的另一点，求出直线PC的解析式，再求点P的坐标.由条件∠PCB=∠CBD得等腰三角形CMB，可尝试其顶点M作为直线PC上的另一点.进而思考顶点M的坐标求法.构造易，思维指向性很强，步步逼近目标求解.

思路4我们很容易发现∠PCO=∠DBO.要求点P的坐标，就是求线段OP的长，而线段OP在直角△PCO中，尝试构造一个包含∠DBO的直角三角形.

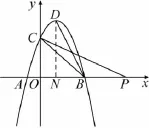
图4

略解4(如图4)作DN⊥OB，垂足为N，

易证△PCO∽△DBN，

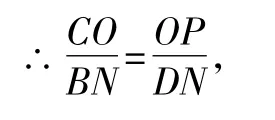
易知线段CO=3，BN=2，DN=4，

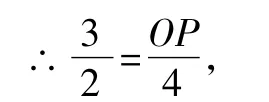
∴OP=6，即P(6，0)

点评点P坐标转化成线段OP的长，目标转换很准确，思维很大胆，构造简单直接.

思路5(如图5)要求点P的坐标，转化成求直线CP的解析式，因为点C坐标已知，从而转化成求直线CP上另一点的坐标.怎样找这一点呢?经过演算，可发现点B，C，D构成一个直角三角形，于是过点B作BE⊥BC交PC于点E，构造△DCB≌△EBC.若能求出点E的坐标，就可以求直线CE的解析式，从而求出点P的坐标.要求点E坐标，就先作垂线.过点D，E分别作出坐标轴垂线，得△DCM≌△EBN，可求出BN，EN，从而求出点E坐标.

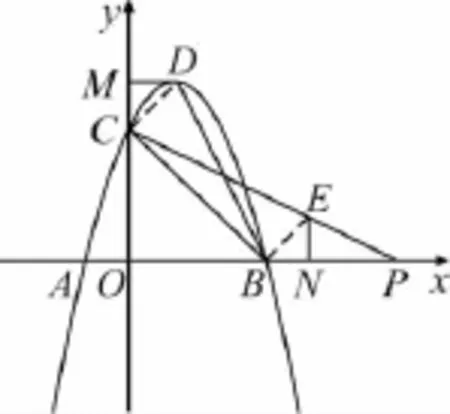
图5

点评与思路3思考方向一致，发现很深入，但求解很复杂.

以上各种求解思路，涉及全等、相似等基本知识，包含转化、构造等基本方法，锻炼学生求异思维.

2 不同的角度提问，培养学生求同思维

变式1假设点P为抛物线上一点，其它条件不变，求点P的坐标.

点评原题中，实际固定了点P的位置.当点P在抛物线上时，则其位置可能在第一象限，也可能在第四象限.在第一象限时，按原题求解，在第四象限时，过点C作BD的平行线交抛物线可求解.这样变式，培养学生全面思考问题的能力，或者说是分类讨论问题的能力.(如图6)

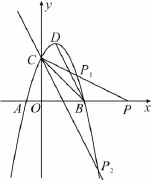
图6

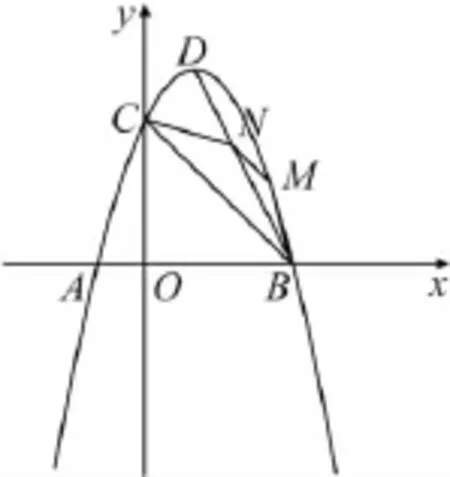
图7

变式2如图7，在线段BD上有一点N，在抛物线第一象限上是否存在一点M，使四边形MNCB为等腰梯形，若存在，求点M的坐标.

点评在抛物线上架构一个等腰梯形，图形变得复杂，由于点M，点N位置都未定，谁先确定也是一个问题，思维更复杂，学生更难把握.培养学生分析问题，透过现象看本质的能力.(提示：由于四边形MNCB为等腰梯形，连接MC，则易得∠MCB=∠NBC，和原题一样.)

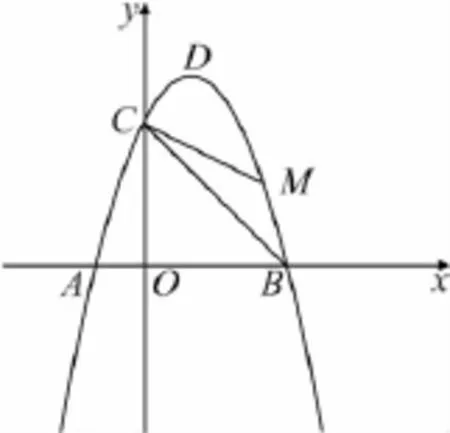
图8

以上各种变式，涉及在抛物线上架构四边形、与三角函数联系，从不同角度看问题本质，都可以转化成原题求解，培养学生的求同思维.

《数学课程标准》提出，数学教学应引导学生通过思考、探索，发展思维，要注重数学知识之间的联系，不断丰富解决问题的策略，提高解决问题的能力.多角度地看同一道问题，最大限度让每一道习题发挥作用，让学生学会分析、学会构造、学会转化，能切实培养学生思维的广度和深度.