把握概念本质 建构生态课堂——对初中数学概念课教学的几点思考

312400 嵊州爱德外国语学校 闾 炜

数学概念是人类对现实世界的空间形式和数量关系的简明概括及反映，它是数学学科的精髓、灵魂.数学概念是进行推理、判断、证明的依据，是建立定理、法则、公式的基础，也是形成数学思想方法的出发点.因此，概念教学在数学教学中有着重要的地位和作用.对数学概念的教学，其“生态课堂”的建构一定要以学生已有的认知基础为出发点，去创设能让学生经历概念的发生、发展过程的教学情境.本文从学生认知基础的角度出发，就概念教学中的课堂建构作简单讨论.

1 把握概念的本质

1.1 内涵和外延

任何一个概念都有它明确的内涵和外延.内涵是指概念所反映的事物的本质属性，通常是通过下定义的方法来表示的，如“函数”的定义是“在某一变化过程中，有两个变量x，y.在某一法则的作用下，如果对于x的每一个值，y都有唯一的值与其相对应，这时，就称y是x的函数.”函数概念的本质：两个变量之间的一种特殊的对应关系.“函数”不是一个数，而是一个对应关系.

外延是指概念所涉及的范围和条件.如“函数”的外延是“在某一变化过程中”，即函数概念所反映的基本思想是运动变化的思想.

1.2 客观和抽象

概念是从客观事物中概括和抽象出来的，它反映了客观事物的本质属性和内在联系，因此，具有客观性.一个概念能够反映出大量形形色色的物质的共同属性，因而具有高度的概括性和抽象性，它超脱了具体的现象而说明了事物的本质.

1.3 发展和变化

概念是在科学实践中逐步形成和发展起来的，一个概念的内涵是否正确，外延是否恰当都要用实践来检验，并随着科学实践的深入发展而不断得到补充、修正和重构.

1.4 联系和结构

概念和概念之间虽然可以进行精确的区分，但它们之间并不是孤立的，它们之间存在着直接的或间接的联系，其主要形式是从属和并列.如四边形是个大概念，平行四边形是个小概念，正方形是个更小的概念，但正方形的四边相等、四角相等、对角形互相垂直平分且相等的共同属性，就比四边形的共同属性四条边、四个角要更多些.

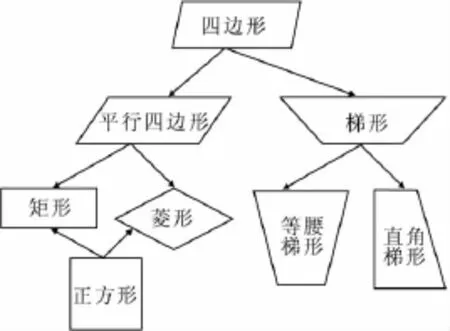
图1

2 概念教学中“生态课堂”的建构的方法

2.1 重视导入，激发思维

数学教学情境的创设，是指在数学教学中对教学内容的呈现采用特定的方法，来达到激发学生主动地联想、想象、积极地思维，以获得某种与新学内容有关的形象或思维成果.在教学时，要根据学生的实际来创设具有启发性的、能激发学生求知欲望的问题情境，使学生用自己的思维方式积极思考、主动探索、创新数学知识.

2.1.1 利用学生在日常生活中熟悉的具体事例进行引入

通过贴近学生的生活实例，来对相应的概念作出解释，使学生从感性认识到理性认识，有利于学生加深对概念的理解.

如：笔者在认识函数(1)时的情境引入：

问题1国家发改委通知，自10月26日零时起，将汽油、柴油的价格上调，上调后的93#汽油零售价为6.53元/升，如果设加油量为x升，应付的金额为y元，你能完成下表吗?

加油量x(升) 1 5 10 15 20 … x …应付金额y(元)

然后回答下列问题：(1)在上述变化过程中，有几个变量?

(2)再给定一个x值，你还能求出相应的y的值吗?

(3)当加油量确定时，应付金额能确定吗?

(4)你能用含x的代数式表示y的值吗?

问题210月26日沪杭高铁正式投入运营，上海至杭州全长202千米，列车从上海到杭州所需的时间为t小时，列车行驶的平均速度为v千米/小时.

(1)在这个变化过程中，有几个变量?

(2)怎么用含v的代数式表示t?

(3)当v=303，350时，你能求出相应的t的值吗?(保留2个有效数字)

(4)再给定一个v值，你还能求出相应的t的值吗?

2.1.2 在旧概念的基础上通过对比、类比引入新概念

又如：在反比例函数的图象和性质的引入部分，此教学设计是类比了正比例函数的图象和性质，先让学生回顾正比例函数的图象和性质，并列出表格，列出解析式、形状、位置、图象趋势、增减性等，接下来类比这些内容研究反比例函数的图象和性质.

2.2 剖析概念，揭示本质

数学概念是用精练的数学语言表达出来的，在教学中，抽象概括出概念后，还要注意深入剖析概念的定义，帮助学生进一步理解概念的含义.

例如，在学习函数概念时：

(1)“在某个过程中，有两个变量x和y”是说明：变量的存在性与函数是研究两个变量之间的依存关系.

(2)“对于在某一范围内的每一个确定的值”是说明变量x是在一定范围内取值，即允许值范围也就是函数的定义域.

(3)“y有唯一确定的值和它对应”说明有唯一确定的对应规律.

(4)“y是x的函数”揭示了谁是谁的函数，由以上剖析可知，函数概念的本质是变量之间的关系.笔者在上认识函数时是这样剖析函数概念的.

第一步：通过上面两个引例，叫学生回答：这些变化过程中，两个变量之间的关系有什么共同点?(在变化过程中，一个量确定，另一个变量也随之唯一确定).

母亲也纳闷儿，这粮食哪来的，问父亲，父亲也不讲。母亲生气了，问，是偷来的吗，这事可不能做，宁愿挨饿，也不能干那事啊！父亲大怒，说母亲侮辱他，告诉母亲这是用汗水挣来的，干净着呢，放心吃吧。

第二步：按学生回答和引例得出函数概念.教师板书并讲解函数的概念要点：变化过程中;两个变量(x，y);x每一个确定的值，y都有唯一确定的值(x叫做自变量，y是x的函数).

第三步：概念辨析：判断下列说法是否正确?为什么?(1)在圆的面积公式S=r2中，S与r之间构成函数关系.(2)已知每支钢笔5元，要买x支钢笔的总价为y元，那么y是x的函数.

第四步：观察生活中所遇到的或者熟悉的某些变化过程是否存在函数关系，让学生尝试用两个变量来描述.

第五步：在学生回答的基础上教师再补充

如：中国2010年上海世博会园区即时客流统计图.

第六步：探究函数关系的表示方法：在前面学生已经接触到的几个函数，教师引导学生归纳总结：

在问题1中，金额y与加油量x的关系y=6.53x.用等式来表示函数关系的方法叫解析法.

如问题2门票张数a(张)与金额b(元)的关系

门票张数(张) 1 3 5 10 20 … t …金额b(元) 160 480 800 1600 3200 … 160t …

把自变量的值和函数对应值列成一个表，这种方法叫列表法.

中国2010年上海世博会园区即时客流统计图：用图象来表示函数关系的方法，叫图象法.

函数概念的得出由学生尝试完成，经过上一环节三个问题的分析，学生体验了函数的发现历程，基本上能够把握住函数概念的关键点.通过学生自己的归纳总结，让学生经历批判和相互推翻的过程，最终由学生将关键点串联，形成与教材接近的函数概念.这样，学生对函数内涵的印象会深刻.

2.3 抓住重点，深化内涵

揭示概念的内涵不仅由概念的定义完成，还常常由定义所推演的一些定理、公式得到进一步理解.如以三角函数的定义为基础，推导特殊角的三角函数值，以及解直角三角形，可使学生清楚地看到概念是学习其它知识的依据.反过来又会使三角函数的内涵得到深入揭示，加深对概念的理解，增强运用概念进行推理判断的思维能力.笔者在教学生解直角三角形时是这样深化三角函数内涵的.

选题如图，京杭运河修建过程中，某村考虑到安全性，决定将运河边一河埠头的台阶进行改造.在如图的台阶横断面中，将坡面AB的坡角由45°减至30°.已知原坡面的长为6cm.(BD所在地面为水平面)

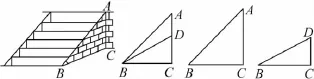
(1)改造后的台阶坡面会缩短多少?

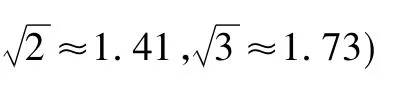
解决这类问题的关键是要回归三角函数定义，找准找对解题所需要的直角三角形.先让学生找出这题目中的直角三角形.然后根据已知条件AB=6cm和三角函数定义在直角三角形ABC中求出AC和BC的长，再利用三角函数定义和BC的长求出BD和CD的长，那么这个题目的答案就找到了.

2.4 归纳总结，区分异同

“有比较才有鉴别”，数学的各种知识要让学生在比较中去思考、去认识.数学的一些概念和规律，理论性较强而且比较抽象，如果把它与学生熟悉的(已知的)相关实体(事物)进行比较，从中理解概念、掌握规律，学生就会对它产生极大兴趣，就会主动思考.如关于“轴对称图形”和“轴对称”这两个概念学生较难理解，但通过让学生观察常见的汽车标志，如奔驰、大众、桑塔那;商标如工行、农行等，看到它们共同的性质：沿某条直线翻折，左右两边能够完全重合，这样就容易理解轴对称概念.

2.5 梳理概念，融汇贯通

数学中的概念，有些是互相联系的，互相影响的，教学完一个单元或一章后，要善于引导学生把有关概念串起来，充分揭示它们之间的内部规律和联系，从而使学生对所学概念有个全面、系统的理解，例如：初中函数从一次函数到反比例函数，再到二次函数，最后是三角函数.学习函数时都是从特殊到一般，从图象到性质，再从性质到应用.

2.6 运用概念，形成系统

概念的形成是一个由个别到一般的过程，而概念的运用则是一个由一般到个别的过程，它们是学生掌握概念的两个阶段.通过运用概念解决实际问题，可以加深、丰富和巩固学生对数学概念的掌握，并且在概念运用过程中也有利于培养学生思维的深刻性、灵活性、敏捷性、批判性和独创性等等，同时也有利于培养学生的实践能力.

运用概念的方法可以是①复述概念或根据概念填空.②运用概念进行判断.③运用概念进行推理.

教学时，应阐明概念之间的内在联系，明确概念的从属关系，科学地、系统地分析概念的相互关系，如四边形认知图式的构建，把四边形(平行四边形、矩形、菱形、正方形等)的知识有机地融合在一起.