四分之一平面域上Helmholtz方程的混合边值问题*

黄民海

(1.中山大学数学与计算科学学院，广东 广州 510275;2.肇庆学院数学与信息科学学院，广东 肇庆 526061)

众所周知，求解偏微分方程有各种各样的方法：分离变量法、傅立叶变换法、格林函数法、逆散射方法，等等。20世纪末，Fokas提出一套新颖灵活的变换方法，用于求解二维线性和可积性非线性偏微分方程的初(边)值问题[1-2]。随后，Fokas和他的学生及其合作者不断改进和完善此方法，取得了一系列的研究成果[3-5]。

利用Fokas方法得到的解，是一个谱平面上包含已知边界值的封闭积分表达式。相比于经典方法，这种积分表达式具有两个重要特点：一是积分路径可以变形到包含指数下降的被积函数的曲线；二是积分在区域的边界上一致收敛。这两个特点可以方便对解作进一步的渐近分析和数值计算[6-7]。

许多时间调和声波或电磁波的散射问题都能表成某个Helmholtz方程[8-9]。本文就是利用Fokas变换方法研究如下1/4平面域上Helmholtz方程的混合边值问题

(1)

r=|z|→∞

(2)

1 解的积分表达式

Fokas变换方法源于逆散射方法，利用到Lax pair和Riemann-Hilbert技术。本节我们将简要推导第一象限(1/4平面)Ω内Helmholtz方程解的一般积分表达式。为了方便后面讨论，这里与Fokas的推导过程稍有改动。

(3)

其中，谱函数ρ1(k)和ρ2(k)分别定义为

q(x,0)]dx,lmk≤0

(4)

q(0,y)]dy,Rek≤0

(5)

而

L1={|k|≤1,argk=π}∪{|k|≥1,

argk=0}∪{|k|=1,π≤argk≤2π},

此外，如下全局关系成立

ρ1(k)+ρ2(k)=0,k∈D

(6)

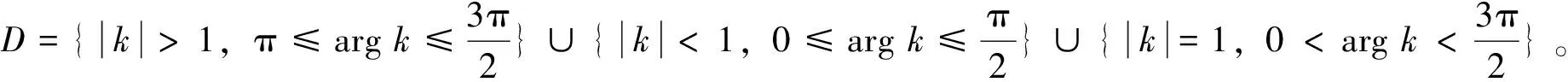
(7)

(8)

由此得到全局关系(6)，其中用到符号：

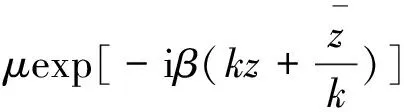
(9)

由(7)和(9)，直接推得Helmholtz方程具有如下的Lax pair：

(10)

相应地固定某点zj，由(9)有

(11)

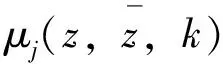
分别取zj为(0,0),(x,∞)和(∞,y)，相应地得到

(12)

(13)

(14)

这里，ζ=ξ+iη，

(15)

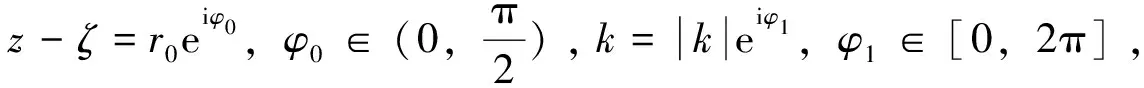
r0sin(φ0+φ1)

(16)

(17)

其中μ=μ0,μi∞,μ∞定义在其相应的有界解析区域D0,Di∞,D∞。

注意到μ∞=μi∞,k∈D，由此，可以定义如下分区全纯函数(与文[3]有所不同)

(18)

从而，可以构造Riemann-Hilbert问题

(19)

(20)

ρ1(k),ρ2(k)称为谱函数，分别由(4)，(5)定义。

根据解析函数边值理论[11]，满足条件(17)的Riemann-Hilbert问题(19)有唯一解

(21)

将(21)代入(10)的第二个方程，得到积分表达式(3)，这样，引理得证。

2 混合问题的解

式(3)和(4)-(5)常称作Fokas变换。一般地，解的积分表达式(3)含有Dirichlet和 Neumann边界值。对于具体问题如本文所讨论的混合边值问题(1)，已知边界Γ1上的Dirichlet边值和Γ2上的Neumann边值，而边界Γ1上的Neumann边值和Γ2上的Dirichlet边值未知。对于一些特定的区域，利用全局关系(6)和某些映射关系，可以消除表达式中的未知量，从而得到解的封闭积分表达式。

(22)

证明引入辅助函数

由全局关系(6)，得

N1(k)+D1(k)+N2(k)+D2(k)=0,k∈D

(23)

N1(-k)-D1(-k)+N2(k)-D2(k)=0,k∈D*

即

N2(k)=D1(-k)-N1(-k)+D2(k),k∈D*

(24)

其中

有效。由(6)和(24)消去N2(k)，得

N1(k)-N1(-k)+D1(k)+D1(-k)+

2D2(k)=0,k=-t,t∈L1

(25)

N1(-k)-N1(k)+D1(-k)+D1(k)+2D2(-k)=0,k∈L1

即

D1(k)=-D1(-k)+N1(k)-N1(-k)-2D2(-k)=0,k∈L1

(26)

由于ρ1(k)=N1(k)+D1(k),ρ2(k)=N2(k)+D2(k)，将(24)，(26)代入(3)，得

其中

利用柯西定理，H=0,再把L2的积分转化到L1上，得到所要证的结论

参考文献：

[1]FOKAS A S. A unified transform method for solving linear and certain nonlinear PDEs[J]. Proc Roy Soc London,Ser A,1997,453:1411-1443.

[2]FOKAS A S. Lax pairs and a new spectral method for linear and integrable nonlinear PDEs[J]. Selecta Mathematica,New ser,1998,4: 31-68.

[3]FOKAS A S. A unified approach to boundary value problems[M]. Philadelphia: SIAM,2008.

[4]DASSIOS G,FOKAS A S. Methods for solving elliptic PDEs in spherical coordinates[J]. SIAM J Appl Math,2008,68: 1080-1096.

[5]FOKAS A S,FLYER N,SMITHEMAN S A,et al. A semi-analytical numerical method for solving evolution and elliptic partial differential equations[J]. J Comp Appl Math,2009,227: 59-74.

[6]FLYER N,FOKAS A S. A hybrid analytical-numerical method for solving evolution partial differential equations,I: The half-line[J]. Proc R Soc London,Ser A,2008,464: 1823-1849.

[7]FOKAS A S,SCHULTZ P F. The long-time asymptotics of moving boundary problems using an Ehrenpreis-type representation and its Riemann-Hilbert nonlinearisation[J]. Comm Pure Appl Math,2002,LVI :1-40.

[8]李松华. 小波在Helmholtz方程和采样中的应用[D]. 广州:中山大学数学与计算科学学院,2006.

[9]张伯坚. 浅海硬障碍物声波的反散射问题[J].中山大学学报:自然科学版,2000,39(4):35-39.

[10]SPENCE E A. Boundary value problems for linear elliptic PDEs[D]. University of Cambridge,2008.

[11]LU C K. Boundary value problems for analytic functions[M]. World Scientific,Singapore,1993.