具有逐段常值变元逻辑方程的全局吸引性

王振芳，罗 芳

（山西大同大学数学与计算机科学学院，山西大同037009）

考虑如下具有逐段常值变元的逻辑方程

其中

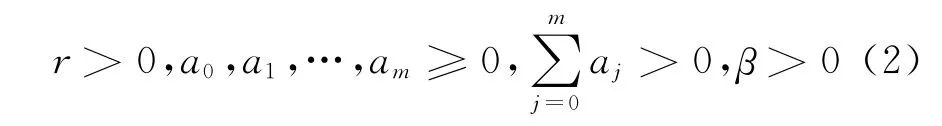
方程（1）有唯一的正的平衡点N＊，它满足

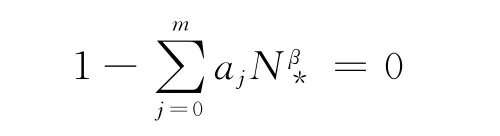
因而

具有逐段常值变元的微分方程是泛函微分方程中的一类重要方程［1]，文献［2 -5] 研究了具有逐段常值变元的微分方程的振动性和稳定性问题．

本文考虑方程（1）的全局吸引性，文献［5] 研究了β＝1时方程（1）的全局吸引性，本文推广文献［5] 中部分结果为β＞0的情形，得到方程（1）为全局吸引的一个充分条件．

令N（t）＝N＊×exp｛x（t）｝，f（x）＝eβx－1，则x（t）满足如下方程

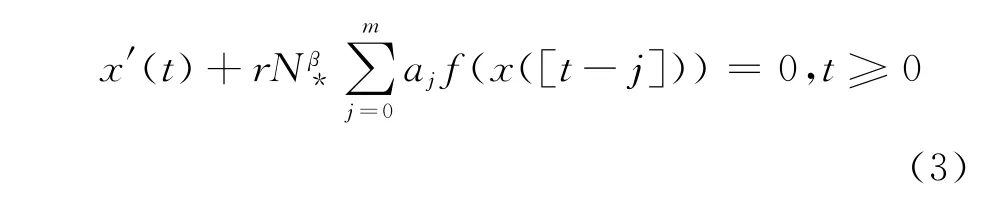
进一步有

其中xn＝x（n），n＝0，1，2，…

下面给出方程（1）为全局吸引的结果．

定理1 设式子（2）成立，且令r1＝若r1，r2满足

r1＞r2＞0，1＜rβ＝（r1＋r2）β≤2．

且

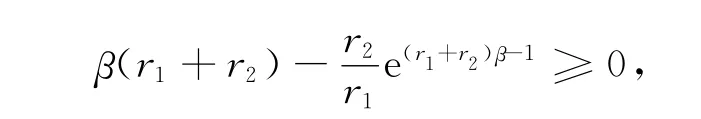
定理1的证明可以由下面几个引理得到．

引理1 令

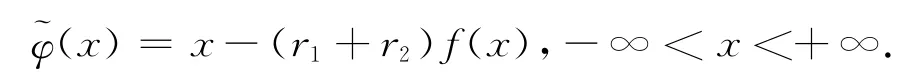
设0＜（r1＋r2）β≤2，则

引理2 设

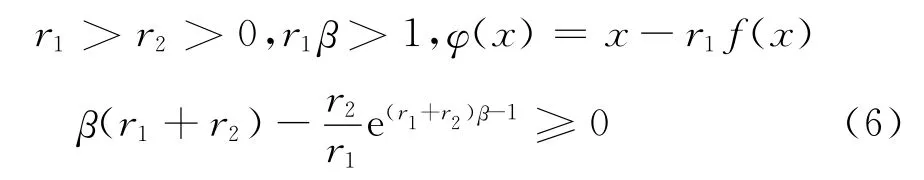
则φ（x）在L＊＝＜0达到唯一的局部最大值．

1）当L≤0时，令G1（L）＝φ（L）－r2＝r1f（L）＋且＝φ（L＊）－r2f（L），则下面的每一条都成立：

iii）若对某个L＜L＊成立（L）＝0，则（L）＜0．

因此，对任意L≤L＊成立（L）＜0且G1（L）＞0．

2）当L≤0时，令G2（L）＝－－L且＝φ（L＊）－r2f（L），则下面的每一条都成立：

ii）G2（L＊）＝（L＊）－L＊＞0；

iii）G′2（L）＜0对任意L≤L＊成立．因此，对任意L≤L＊有G2（L）＞0成立．

3）当L≤0时，令G3（L）＝－－L且＝φ（L）－r2f（L），则对任意L＊≤L＜0，G3（L）＝（L）－L＞0．

引理3 设1＞r1β＞r2β＞0，（r1＋r2）β＞1，

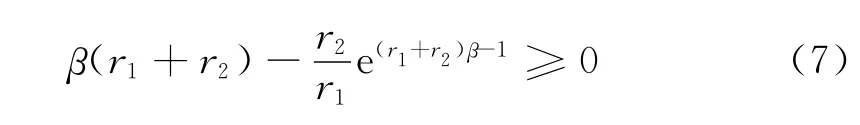
则φ（x）在R＊＝－＞0取得唯一局部最大值．

1）当L≤0时，令G4（L）＝φ（L）－L（L）＝r1f（L）＋r2f，且＝φ（R＊）－r2f（L），则存在唯一L¯＜0，使得

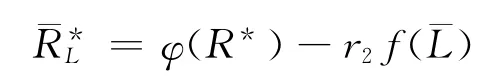
且下面的每一条都成立：

2）当L≤0时，令

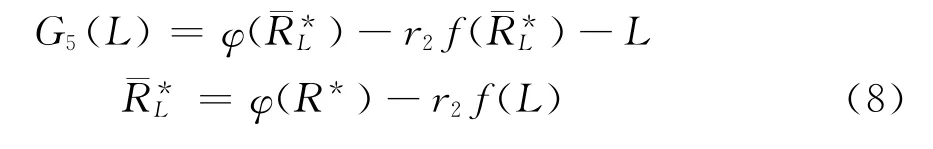
G5（L）＝－L＞G4（L）＞0．

引理4 设

则φ（x）在R＊＝0取得唯一局部最大值，因而文献［5] 中（2．22）—（2．23）成立，且有下面结论．

1）在引理3的1）中考虑R＊＝0时的函数G4（L），有L＜＝0时，G4（L）＞0成立．

2）在式（8）中，R＊＝0时，G5（L）＝L＞0对任意L＜＝0成立．

证明 证明定理1的条件可分为引理2、引理3与引理4的条件考虑，因而，由引理2、引理3与引理4可证＝0，从而定理1得证．

注：对于情形0＜r1≤2，r2＝0与情形0≤r2＜r1，（r2＋r1）β≤1也可证明方程（1）有全局吸引性，但与本文的方法不同．

［1] 郑祖庥．泛函微分方程理论［M] ．合肥：安徽教育出版社，1994．

［2] Gopalsamy K，Ladas G．On the oscillation and asymptotic behavior of N＇（t）＝N（t）［a＋bN（t－τ）] －cN2（t－τ）［J] ．Quarterly of Applied Mathematics，1990，XLVIII：433－440．

［3] So J W H，Yu J S．Global stability in a logistic equation with piecewise constant arguments［J] ．Hokkaido Math．J．，1995，24：269－286．

［4] Muroya Y．A sufficient condition on global stability in a logistic equation with piecewise constant arguments［J] ．Hokkaido Math．J．，2003，32：75－83．

［5] Uesugi K，Muroya Y，Ishiwata E．On the global attractivity for a logistic equation with piecewise constant arguments［J] ．J．Math．Anal．Appl．，2004，294：560－580．