基于小波的加外生变量部分线性自回归模型在石油价格预测中的应用

井霞霞，张德生，李金凤，王彦彪

（西安理工大学理学院，陕西西安710054）

准确的预测石油价格变动的方向和程度对国家制定能源政策和规避价格风险具有重要意义，对维护石油生产国和消费国的利益亦有重大意义．

目前预测石油价格的主要方法有时间序列法［1]、层次分析法［2]、灰色预测法［3]、回归分析法［4]．时间序列模型主要有AR模型、ARMA［5]模型、ARIMA模型、VAR模型［8]、ARCH模型［9]、GARCH模型［10]、变系数回归模型［11]等．

1 部分线性自回归模型

部分线性模型［12]的一般形式为

其中Xt－1＝（xt－1，1，…，∈Rp和Zt－1＝（zt－1，1，…∈Rq为解释变量；β＝（β1，…，为未知参数向量，p和q是正整数，Yt∈R为响应变量或者是解释变量．g（·）是未知函数，｛εt｝为随机误差序列，且εt＝Yt－E［Yt｜Xt－1，Zt－1] ，为线性时间序列部分，g（Zt－1）是非线性时间序列部分．在（1）式中，如果Xt－1和Zt－1中有一个是Yt的滞后变量，则（1）式就是部分线性自回归模型．

2 小波多分辨分析

Meyer于1986年创造性地构造了具有一定衰减性的光滑函数，其二进制伸缩与平移构成L2（R）的规范正交基，才使小波得到真正的发展；1988年Mallat在构造正交小波基时提出了多分辨率的概念，从空间的概念上形象地说明了小波的多分辨率特性，将之前的所有正交小波基的构造法统一起来，给出了正交小波的构造方法以及正交小波变换的快速算法，即Mallat算法．Mallat算法在小波分析中的地位相当于快速傅立叶变换算法在经典傅立叶分析中的地位［13]．

定义1 设L2（R）的闭子空间序列｛vk，k∈Z｝称为形成一个多分辨分析，若这些闭子空间｛Vk｝满足以下性质：

1）单调性：Vm⊆Vm＋1，m∈Z．

3）伸缩性：

4）平移不变性：

5）Riesz基存在性：存在Ψ（x）∈V0，使得｛φ（x－n）｜n∈Z｝构成子空间V0的Riesz基．

则称｛Vk｝这些闭子空间成了L2（R）的一个多分辨分析，其中φ（x）称为尺度函数，此时称φ（x）生成了一个多分辨分析为｛Vk｝．

多分辨分析理论认为一个信号可以分解为低频信号（概貌序列分量）和高频信号（细节序列分量）两部分．

3 基于小波的考虑外生变量的部分线性自回归模型

3．1 建模步骤

对WTI石油价格进行建模预测时，具体步骤如下：

（1）利用小波变换对WTI现货价格序列和世界供应量分别进行分解和重构，得到相应的概貌序列分量和细节序列分量，然后对他们分别进行平稳性检验和平稳化处理．

（2）利用概貌石油价格序列分量和概貌世界供应量序列分量建立部分线性自回归模型．

（3）对细节石油价格序列分量和细节世界供应量序列分量也建立部分线性自回归模型．

（4）将WTI现货概貌价格和细节价格的预测结果进行求和，可以得到最后的WTI现货预测价格

3．2 样本选取

本文所选取的数据是2004年1月到2011年2月的WTI现货价格和世界供应量的月度数据共86个，数据来源于美国能源情报署（http：／／www．eia．doe．gov／），前80个数据用于建模，后6个数据用来评价模型的质量．

3．3 小波分解与重构

对WTI现货价格序列采用Sym2小波进行一层小波分解与重构，得到低频的概貌序列CA1和高频的细节序列CD1，如图1所示．从图1可以看出，在一层分解重构下得到的概貌序列基本上已经反映了WTI现货价格序列的波动趋势，而细节序列则体现了WTI现货价格序列的随机波动，分解的效果较好．同样对世界供应量用Sym2小波进行小波分解和重构，得到相应的概貌序列和细节序列．

图1 分解与重构后的概貌序列和细节序列

3．4 平稳性检验和预处理

在建立模型之前需要对WTI现货价格和世界供应量进行小波分解和重构后的概貌序列和细节序列进行平稳性检验和平稳性处理，采用ADF检验法对概貌序列和细节序列分别进行检验，见表1．WTI现货价格和世界供应量的概貌序列的ADF检验结果的统计量都大于各显著性水平的临界值，所以应该接受原假设，即WTI现货价格和世界供应量的概貌序列并不平稳，经过对数差分后，ADF检验结果的统计量均小于各显著性水平的临界值，所以应该拒绝原假设，即序列平稳，而它们的高频序列由表1可以看出已经平稳，故不需要处理．

3．5 部分线性自回归模型的建立

对经过平稳化处理后的WTI现货价格小波分解重构后的概貌序列进行建模，其中参数部分选取WTI现货价格，非参数部分选择世界供应量．建立的部分线性自回归模型的表达式为

表1 ADF检验结果

对WTI现货价格经过小波分解的细节序列进行建模，建立的部分线性自回归模型的表达式为

通过以上两个模型可以分别得到建模数据的概貌序列和细节序列的拟合值，应用MATLAB编程，将WTI现货价格概貌序列的拟合值进行还原，并与细节序列的拟合值进行相加得到WTI现货价格最终的拟合值．

基于小波的考虑外生变量的部分线性自回归模型对WTI现货价格的拟合值和真实值比较结果如图2所示．从图2可以看出，基于小波的考虑外生变量的部分线性自回归模型对WTI现货价格月度数据时间序列的拟合效果比较准确．

图2 部分线性自回归模型拟合图

3．6 部分线性自回归模型的检验

当建立好一个时间序列模型时，需要检验随机误差项｛εt｝是否是一个白噪声，若是则可以认为所建模有效，本文利用χ2检验法来进行检验，其主要思想是将εt的自相关系数记为ρk（N，εt），自协方差函数记为γk（N，εt），则

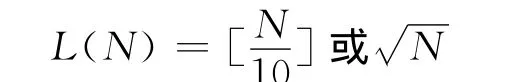
假设1 H0～NID（0，1），那么，即Q＝服从自由度为L（N）－M的χ2分布，L（N）为自相关系数的个数，M为模型的参数个数，于是，在给定显著性水平α下，若Q≤（L（N）－M）接受H0；若Q＞（L（N）－M）则拒绝H0，即否定εt独立．

由于εt是随机的，这里我们用＝Yt－，t＝1，2，…，N来表示．所以由上述分析可知N＝80，L（N）＝10，M＝1，故L（N）－M＝9；当α＝0．05时，查χ2分布表可知（L（N）－M）＝（10－1）＝（9）＝16．919

概貌序列所建模型的统计量Q＝14．7023＜16．919，所以有95%的置信度认为残差序列是白噪声序列，因此，所建立的部分线性自回归模型是有效的．

细节序列所建模型的统计量Q＝2．2243＜16．919，所以有95%的置信度认为残差序列是白噪声序列，因此，所建立的部分线性自回归模型是有效的．

3．7 模型的预测比较

为了更好的研究所建立的模型的优劣，对部分线性自回归模型、考虑外生变量的部分线性自回归模型和基于小波的考虑外生变量的部分线性自回归模型的预测结果进行比较，结果见表2，并计算出其平均绝对误差和均方误差，结果见表3．

表2 3种模型的预测效果及其比较 美元／桶

表3 预测结果的MAE和MSE的比较

相对误差＝（实际值—预测值）／实际值．

实证结果表明，对部分线性引入外生变量后，提高了模型的解释能力，从表3中可以看出预测精度得到了一定的提高，将小波与考虑外生变量的部分线性自回归模型结合以后，预测精度得到了进一步的提高．

4 结束语

本文对WTI现货价格序列建立了基于小波的且考虑外生变量的部分线性自回归预测模型，并将该模型与部分线性自回归预测模型和考虑外生变量的部分线性自回归预测模型进行了比较分析，因为该模型既利用了小波分析良好的局部化特性，又考虑了外生变量对外界影响因素的响应性，因此具有较高的预测精度．

［1] Granger C W J，and New bold．Spurious regession in econonetrics［J] ．Journal of Econometrics，1974，2：111－120．

［2] Yang C W，Hwang M J，Huang B N，An analysis of factors affecting price volatility of the US011market［J] ．Energy Economics，2002，24：107－119．

［3] 华泽澎，方红松．国际油价的影响因素分析及中长期趋势预测［C] ／／国际石油经济研讨会论文集，1995：43－51．

［4] Hsu L C，Applying the grey prediction model to the global integrated circuit industry［J] ．Technological Forecasting ＆Social Change，2003，70：563－574．

［5] 周明磊．事件对国际石油价格影响的时间序列分析［J] ．数学的实践与认识，2004（8）：12－18．

［6] 丁静之，林怡．ARIMA模型在石油价格预测中的应用［J] ．物流技术，2008，27（10）：156－160．

［7] 肖龙阶，仲伟俊．基于ARIMA模型的我国石油价格预测分析［J] ．南京航空航天大学学报：社会科学版，2009，11（4）：41－46．

［8] 蔡纯．石油价格波动金融影响因素的实证研究——基于月度数据的VAR模型分析［J] ．价格理论与实践，2009（10）：52－53．

［9] 潘慧峰，张金水．基于ARCH类模型的国内油价波动分析［J] ．统计研究，2005（4）：16－20．

［10] 邹艳芬，陆宇海．基于GARCH模型的石油价格变动模拟［J] ．数理统计与管理，2006，25（6）：640－644．

［11] 舒通．基于变系数回归模型的石油价格预测［J] ．数理统计与管理，2008，27（5）：815－820．

［12] 柴根象，洪圣岩．半参数回归模型［M] ．合肥：安徽教育出版社，1995．

［13] 程正兴．小波分析算法与应用［M] ．西安：西安交通大学出版社，1998．