低速状态下遗传神经网络直接转矩控制
张 莲,赖 伟,李 洁,李文娟
(重庆理工大学,重庆400054)
0 引 言
1 直接转矩控制原理
直接转矩控制系统采用定子磁场定向,将定子电流、电压进行3/2变换,从而直接在静止α-β坐标系下计算交流电动机的转矩和磁链,再分别与给定转矩和磁链进行比较。根据比较结果查找最优开关表格产生PWM信号,直接对逆变器的开关状态进行控制,系统结构图如图1所示。
在 α - β 坐标系下,磁链方程[1-2]:

根据定子电流、定子磁链,可以计算出电磁转矩:
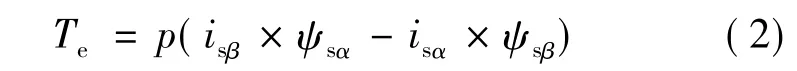
式中:s、r表示定、转子分量;α-β表示两相静止坐标系的坐标轴;usα、usβ分别为定子在 α - β 轴上的电压分量;isα、isβ分别为定子在 α - β 轴上的电流分量;Rs为定子电阻;p为极对数。
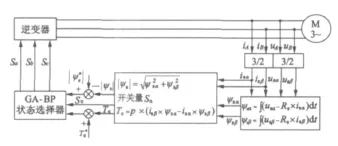
图1 控制系统结构图
2 遗传神经网络(GA-BP)控制器的设计
遗传神经网络算法是将遗传算法和神经网络算法相结合,首先利用遗传算法的全局优化搜索的优点,来获得BP网络的优化系统解,然后将神经网络算法进行自学习,更新网络权值和阈值,得到系统的准确解,使该解为全局最优,避免解为局部最优解的情况。
本文对隐含层节点数选择方法如下[3]:
(1)由式(3)隐含层节点数大致取值范围在区间[4,13]:
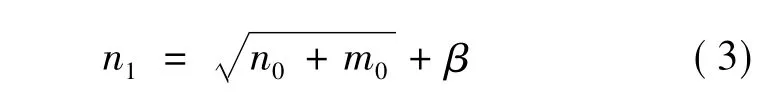
式中:n1为隐含层节点数;m0为输入层节点数;n0为输出层节点数;β为补偿系数。
但是,由于地理、气候条件限制,加上易受寒害和台风影响,广东垦区自有的橡胶产量一直难以有重大突破。鉴于此,近十多年来,我们在国家深化改革开放、鼓励企业“走出去”发展的背景下,坚持统筹国内外资源,在巩固国内天然橡胶基地建设基础上,突破资源瓶颈,提出了“海外再造新广垦”的战略,把目光投射到北纬十七度以南,到东盟国家发展天然橡胶产业,保障国家战略资源安全和经济发展需要。2004年开始谋划,2005年首个天然橡胶海外加工厂在泰国沙墩府落成并投入使用。截至目前,广东农垦已在东盟和非洲投资建设了天然橡胶、剑麻、木薯等45个热作生产经营项目,累计投资32亿元,正在实施的海外热作产业面积约200万亩。
(2)通过试验隐含层节点数确定为7个。

图2 3-7-3神经网络模型
遗传算法优化BP网络初始权值和阈值[4]的步骤如下。
(a)编码长度的选取与初始种群的建立:本文采用上述3-7-3的BP网络结构,设输入层、隐含层与输出层节点的个数分别为R、S0和S1,则编码的长度:
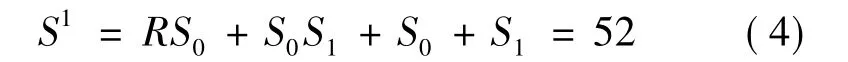
随机生成L个编码长度为S1染色体,即建立起初始种群。
(b)适应度函数:把上述建立起种群中的S1个连接权值赋予神经网络,仿真计算BP网络的仿真输出值,并将该值减去期望输出值的平方和设为E(i),则可得到适应度函数:

从该式可以看出,适应度f(i)越高(即误差平方和越小),神经网络性能就越好。
(c)适应度排序:利用下式计算出每个个体被选中的几率:

从上式可得,适应度与选中该个体的概成正比。
(d)新种群的建立:通过交叉、变异等得到与原个体不同的新个体,并将新个体加入原来的种群中,从而建立起新的种群。重新计算出新个体适应度,并判断是否符合要求,若符合要求,则执行下一步,否则重复操作。
(e)神经网络初始结构的建立:将满足要求或最大遗传代数后的最优个体进行解码,从而获得神经网络初始结构参数。
3 遗传神经网络(GA-BP)的DTC控制仿真实现
遗传算法的种群数设为100个,交叉概率设为0.6,遗传代数是600代,变异概率0.01。遗传神经网络的适应度和性能与测试曲线如图3所示。
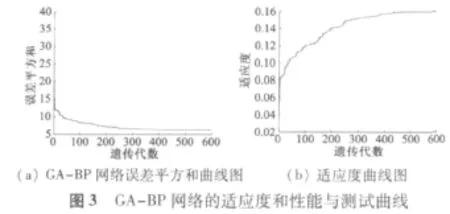
利用得到的BP神经网络的权值和阈值,在Simulink中建立BP网络如图4所示。
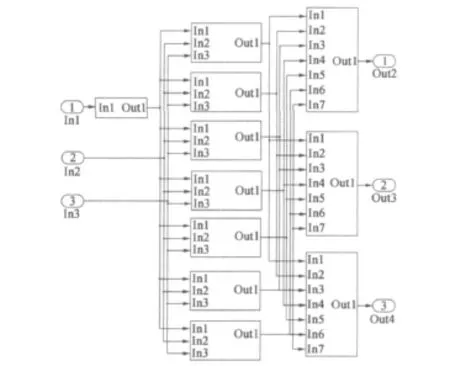
图4 BP网络
仿真时电机各参数:功率P=3 730 W,转子电感 Lr=0.005 974 H,定子电阻 Rs=1.115 Ω,转子电阻 Rr=1.083 Ω,定子电感 Ls=0.005 974 H,互感Lm=0.203 7 H,转动惯量 J=0.02 kg·m2,p=2,电机的阻尼系数RΩ=0,极对数,转矩Tm=20 N·m,转速n=50 r/min。根据上述参数建立直接转矩控制的仿真模型如图5所示[5]。

图5 系统仿真图
运行结果如图6所示,与传统直接转矩控制相比,GA-BP在低速状态下转速脉动更小,具有更高的稳定精度和良好的静、动态性能。

4 结 语
本文首先选取了BP神经网络的隐含层节点个数,再确定了BP网络的结构;利用遗传算法来获取BP神经网络的初始权值和阈值的优化解,并将得到的权值与阈值赋予BP神经网络,建立直接转矩控制的模型。通过GA-BP神经网络和传统DTC控制的仿真结果,证明了GA-BP神经网络模型用于直接转矩控制在低速状态下的可行性、客观性,克服了传统直接转矩控制在低速状态下的问题。
[1] 冯江华,陈高华,黄松涛.异步电动机的直接转矩控制[J].电工技术学报,1999,14(3):29 -33.
[2] 顾德英,季正东,张平.基于SIMULINK的异步电机的建模与仿真[J].电力系统及其自动化学报,2003,15(2):71 -73.
[3] Yu J J,Zhang K J,Fei S M.Improved results on passivity analysis of discrete-time stochastic neural networks with time-varying delay[J].Journal of Central South University(Science and Technology),2009,40(1):63 -67.
[4] 智晶,张冬梅,姜鹏飞.基于主成分的遗传神经网络股票指数预测研究[J].计算机工程与应用,2009,45(26):210 -212.
[5] Wei X,Chen D Y,Zhao C Y.Minimization of torque ripple of direct-torque-controlled induction machines by improved discrete space vector modulation [J].Electric Power Systems Research(S0378 -7796),2004,72(8):103-112.

