实心转子异步电动机的设计研究
胡 岩,刘 涛,陈金哲
(沈阳工业大学,吉林沈阳110023)
0 引 言
实心转子异步电动机采用与普通异步电动机相同的定子结构,但其转子采用实心铁磁体,该实心铁磁体融转子磁路和转子电流路径为一体[1]。这种实心转子异步电动机与普通异步电动机转子结构上的不同决定了两者性能方面的不同。实心转子异步电动机转子为实心铁磁体,与普通异步电动机鼠笼式转子结构相比较,结构简单得多,并且实心转子机械强度高,采用此种转子结构的电机适用于高速运行场合;起动转矩大,起动电流小,适用于重载起动场合;起动电流小,可以在线路过长,压降过大,以及发电机与电动机功率接近的供电系统中应用;机械特性软,转矩转差率具有线性关系,并且实心铁磁体转子热稳定性好,可长时间处于制动状态,适合于挖掘机应用场合;运行时较低的振动和噪声,减小了噪声污染;较宽的调速范围,使其适用于调压调速的场合[2-4]。另外,实心转子电机还适用于频繁起动[5]、频繁正反转及反复短时工作的场合[6-7]。
实心转子异步电动机的转子采用铸铁或铸钢材料,融电路与磁路为一体,在大转差率运行时,集肤效应比较强烈,涡流及磁通集中在转子表面,电阻和转子表面损耗很大。实心转子轴向有限长,通过端部区域,涡流回路闭合,转子阻抗增大[8-9]。转子参数是转差率的函数,不同转差率下,阻抗不同,这将会给实心转子异步电动机的设计带来很大困难。
本文采用透入深度法与多层理论法进行电机设计,与实验数据进行了比较,分析了两种方法的优缺点及各自产生较大误差的原因。本文提出了结合两种方法共同指导实心转子异步电机的设计。研究结果表明,此两种方法结合使用,计算简便,并可综合考虑饱和、端部、曲率效应的影响,提高了实心转子异步电动机的设计精度。
1 对转子参数应用透入深度法的分析与计算
1.1 等效电路及计算原理
实心转子异步电动机采用与普通异步电动机相同的定子结构,可采用如图1所示的T形等效电路来分析和研究实心转子异步电动机。
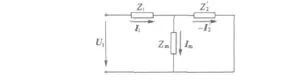
图1 实心转子异步电动机的等效电路
用透入深度法对实心转子异步电动机转子参数进行计算时,假设转子为半无限大的铁磁平板,由于转子涡流的阻尼作用,从气隙侧传来的电磁波在透入铁磁介质的过程中衰减。因此,在应用此种对实心转子参数进行分析和计算时,需作如下基本假设:
(1)假设转子为半无限大铁磁介质平板;
(2)涡流只在宽度为πD2、厚度为Δ、长度为L2的薄层,即转子透入深度区域内流动;密度以2τ为周期沿平板宽度方向,即转子切向按正弦规律分布;
(3)在透入深度区域内,涡流密度为常值,即均匀分布;
(4)只存在轴向涡流,忽略径向和切向涡流。
基于以上假设,转子参数求取可用以下表达式:

式中:ρ为铁磁体的电阻率;L2为转子轴向长度;A为涡流流通面积,可用下式计算:

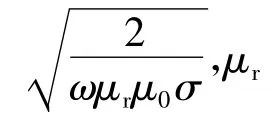
由于转子阻抗角φ2基本上保持为常数,因此,可由R2计算出X2和Z2。实心转子表面存在强烈集肤效应并且转子轴向长度为有限长,因此应用曲率系数、端部系数以及电阻增加系数对转子阻抗计算值予以修正。
同普通异步电动机一样,在不同转差率下运行,转子参数在由转子侧向定子侧折算过程中,需要进行频率折算,即:

由式(3)可以看出,改变转差率s值,可以得出不同转差率下的转子阻抗,进而可以计算出电机性能参数。
1.2 实验验证及计算结果分析
由转子阻抗角表达式:

及推导公式可知,转子阻抗计算中需要乘以不同系数予以修正,因此:

式(5)代入式(4)可得:
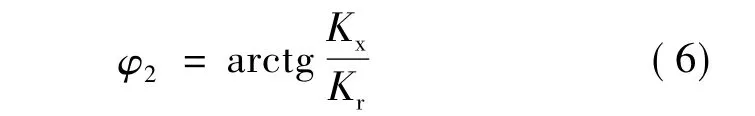
由式(6)可以看出,关键在于合理选取Kr与Kx,转子阻抗角的大小取决于两个系数的比值。以前学者提出φ2一般为35°左右。本文考虑工程实践,选取 Kr=1.25;Kx=0.945,φ2=35.9°。
由图2可以看出,频率折算前,随转差率增大,转子电阻增大,转子电抗减小。频率折算后,随转差率增大,转子阻抗均减小。这是因为转差率增大,由于集肤效应与端部效应增大,转子电阻增大,但电阻变化小于转差率变化。
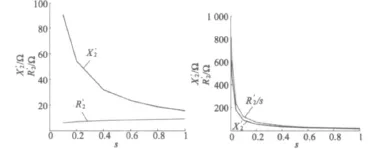
图2 转子阻抗随转差率的变化


表1 实心转子异步电动机的额定数据


设计了一台4极、7.5 kW实心转子异步电动机,样机如图3所示。可以看出,实心转子异步电动机的转子结构易生产加工。转子用10号钢直接浇铸而成,生产成本低。实心转子异步电动机的额定数据与主要尺寸如表1所示。通过对样机进行测试,对测试结果与理论计算结果进行了比较,试验值与计算值的对比如图4~图5所示。由图可知,电磁转矩的计算值与实验值在大转差率下非常接近,而定子电流的计算值与试验值在大转差率下相差很大;定子电流的计算值与实验值在小转差率下的差距缩小,但误差仍较大。
透入深度法计算数值与实验数值存在较大误差的原因:第一,由透入深度的定义可知,当导体电流密度由表面沿实心转子径向向里衰减至0.368倍时,透入深度即指该处到转子表面距离。而此处默认转子涡流只存在于铁磁体透入深度范围内,因此,这种假设将会造成较大误差;第二,在计算转子内磁场强度时,忽略磁场强度切向分量,仅计及脉动磁场的影响;第三,依赖于设计经验的电阻修正系数Kr与电抗修正系数Kx具有不确定性;第四,沿厚度Δ的涡流密度假设是均匀分布的。
2 对转子参数应用多层理论的分析与计算
2.1 计算原理和基本假设
在处理复合转子异步电动机电磁场问题时,多层理论是一种很有效的解析方法。应用这种方法时,将定、转子及气隙沿电动机径向划分为很多层,各层材料特性,如电导率、磁导率及各电磁场量的角频率均可以为不同值。由麦克斯韦方程组和边界条件,可以得出相邻层间电磁场量的传递矩阵,利用此矩阵,可求解出电动机内的电磁场量。这种方法的主要优点在于,一是可以计及铁磁材料沿径向的非线性磁化情况;二是以上所建立的传递矩阵方程仅为二阶复方程,计算过程比较简单。通过上述方法计算可以得出各层电磁场量及其沿径向的变化情况。再由波阻抗概念,就可计算出复合转子异步电动机的参数及性能。应用此方法,需要进行如下假设:
(1)定子为三相对称绕组,外施三相对称电压,定子绕组电流表示为分布于定子内表面的面电流。通过气隙系数Kc计及定子槽开口的影响;
(2)定、转子轴向长度为无限长,通过端部系数计Ke及端部效应;
(3)不考虑铁心材料的磁滞效应,也不计定转子的曲率效应;
(4)定子铁心不饱和,其磁导率和电导率分别假设为无穷大和零;
(5)各电磁场量只计及的基波分量,且忽略位移电流影响。
通过以上假设,可以建立如图6所示的光滑实心转子模型。将实心转子沿径向划分成N-1层,μ、σ和ω在各层内均为同一常数。气隙层磁导率μ0为一常数,电导率σ=0,而且气隙长度δ相对较小,所以在此可将气隙单独划分为一层,为第N层。
定子内表面电流密度表达式:


图6 实心转子异步电动机转子分层示意图
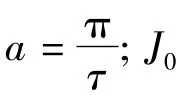

式中:NΦ1Kdp1为每相串联有效导体数;m1为定子相数;Di1为定子内径;I1为定子相电流。
其中,ex、ey、ez分别为 x、y、z方向的单位矢量。并设:
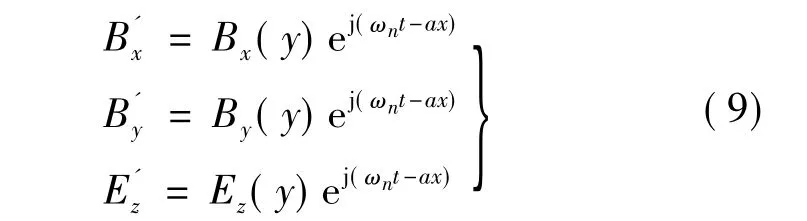
则当n=N时,ωn=ω1;当 n=1~(N-1)时,ωn=sω1。s为转差率。
由麦克斯韦方程组:
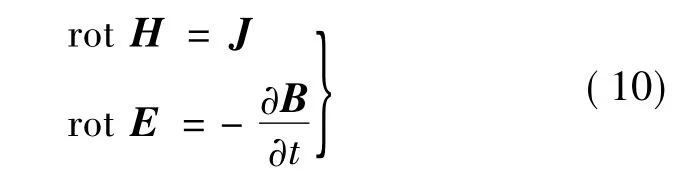
及介质方程:

可以得出:
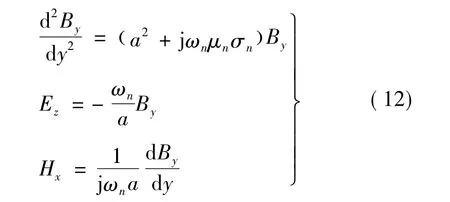
取第N-1层与第N层交界处为y=0,则由边界条件:
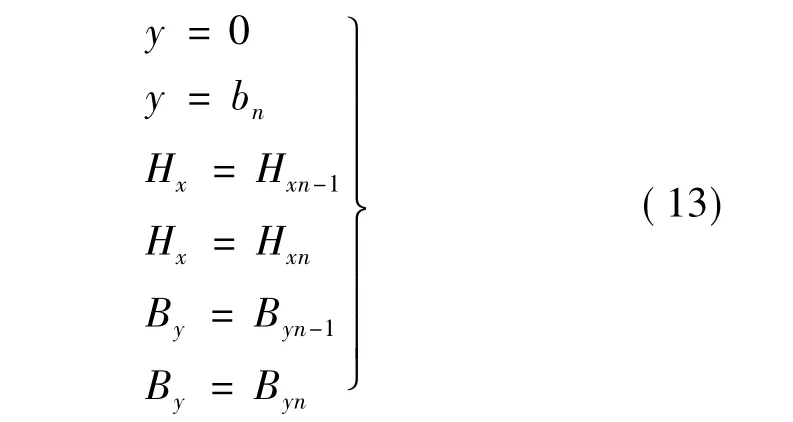
式中:bn为第N层厚度;Hxn为第N层靠近气隙侧边界处磁场强度切向分量,其余如此类推。
由式(12)与式(13)可得出各层场量传递矩阵方程:

当已知第 N -1 层的 Byn-1、Hxn-1时,第 N 层的Byn、Hxn即可求出,从而可以进一步求出 Ezn及 Jxn。对于第 N 层,即气隙层,μn= μ0、σn=0、γn=a 和 bn=Kcδ,即为有效气隙长度。
总体边界条件:

各电磁场量计算出后,转子阻抗即可由波阻抗理论求得。在转子、气隙的交界处,从气隙侧往转子侧看,将转子阻抗折算到定子侧并考虑实心转子端部效应时,可表达:
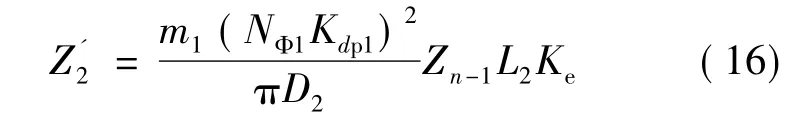
式中:L2为定子铁心有效长度;D2为转子直径;Zn-1为波阻抗。
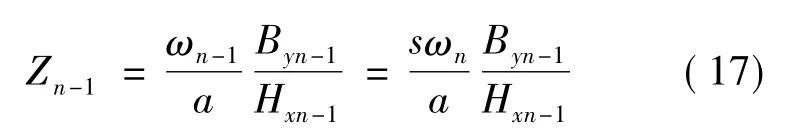
式中:Byn-1、Hyn-1分别为转子表面的径向磁密和切向磁场强度。
2.2 实验验证及计算结果分析
一般情况下,计算结果的精度随转子分层数的增加而相应提高,但计算时间也会随之增长,而由迭代过程中所累积的误差也越大,因此本文在对转子进行分层时将转子层数设为40层。由于集肤效应,越靠近实心转子表面,磁饱和程度越高,磁场与电流密度变化也就越快,所以本文按层厚依次递减对转子分层。计算结果如图7~图9所示。
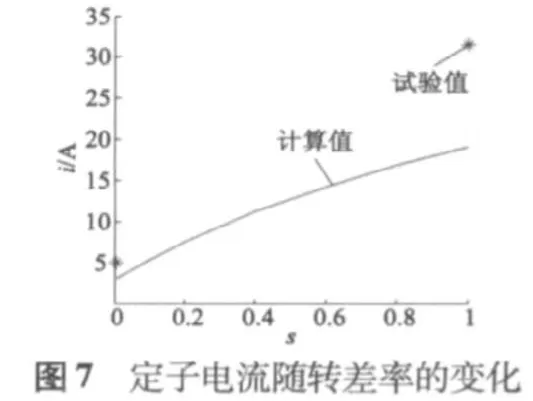


从图中可以看出,应用多层理论求解的转子电流在整个转差率变化范围内较透入深度法与实验值更为接近些,但两者之间仍存在较大误差;电磁转矩的计算值与实验值在大转差率下误差很大,因此不宜采用多层理论法在大转差率下计算电磁转矩。
多层理论法计算结果与实验结果相比,两者之间存在较大误差的原因如下:第一,多层理论法虽然能考虑径向转子磁密分量的变化,但转子磁密沿周向的变化却未曾考虑,因为此方法默认气隙磁密在每层均匀分布;第二,认为铁心磁导率无穷大,这样就忽略了定子铁心非线性所带来的影响;第三,忽略了定子开槽效应及转子曲率效应;第四,转子层厚设置及由此产生的层数多少也会影响计算精度。
3 结 语
应用透入深度法与多层理论法对实心转子参数计算研究表明:对定子电流的计算,应用多层理论法计算相对准确,而应用此法对电磁转矩存在很大误差;在大转差率下,对电磁转矩应用透入深度法计算较准确,应用此法对定子电流的计算则相对存在很大误差。因此,本文提出结合两种方法共同计算转子参数,对电磁转矩计算应用多层理论法,对定子电流计算刚采用多层理论法,结合两种方法来共同设计实心转子异步电动机。此两种方法综合考虑了饱和效应、端部效应、曲率效应的影响,满足工程上对设计精度的要求。
[1] 傅丰礼,唐孝稿.异步电动机设计手册[M].第二版.北京:机械工业出版社,2006.
[2] 谢德馨,姚缨英,白保东,等.三维涡流场的有限元分析[M].北京:机械工业出版社,2001.
[3] 童钟良.双层实心转子感应电机的分层阻抗理论[J].电工技术学报,1993(2):18-22.
[4] Huppunen J,Pyrhonen J.Filtered PWM -inverter drive for high -speed solid - rotor induction motors[J].Industry Applications Conference Record of the 2000 IEEE,2000,3(8 -12):1942 -1949.
[5] 辜承林,陈乔夫,熊永前.电机学[M].第二版.武汉:华中科技大学出版社,2005.
[6] 冯尔健.铁磁体实心转子异步电机理论与计算[M].北京:科学出版社,1980.
[7] 林瑞光.电机与拖动基础[M].杭州:浙江大学出版社,2004.
[8] 黄国治,傅丰礼.中小旋转电机设计手册[M].北京:机械工业出版社,2007.
[9] 汤蕴璆.电机内的电磁场[M].第二版.北京:科学出版社,2005.

